ARTÍCULO ORIGINAL

 

Simulación del vaciado continuo de perfiles de aceros al carbono de baja aleación

 

Simulation of the continuous casting of low carbon steel profiles

 

 

Yusdel Díaz-Hernández,^I Alberto Fiol-Zulueta,^I José Arzola-Ruiz,^II

^I Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Mecánica. La Habana. Cuba.
^II Instituto Superior Politécnico José Antonio Echeverría. Centro de Estudios de Matemáticas. CEMAT. La Habana. Cuba

 

 

---

RESUMEN

En este artículo se presentó un algoritmo para simular el proceso de vaciado continuo a partir de la construcción de un modelo físico matemático utilizando el Método de los Elementos Finitos. Como característica más destacada del algoritmo se encuentra la consideración de los procesos complejos de intercambio de calor, cambio de fase del metal, distribución de temperaturas en el molde, composición química del metal, flujo de agua en el enfriamiento primario y secundario, y la velocidad de colada. El algoritmo permitió predecir con suficiente pericia el comportamiento de las variables durante el proceso de vaciado continuo de acero según perfil y marca del mismo.

Palabras claves: simulación, solidificación, vaciado continuo, modelado.

---

ABSTRACT

In this paper an algorithm to simulate the process of continuous casting based on a physical -mathematical model using finite element methods was presented. The most outstanding characteristic of the model was the inclusion of complex processes of heat interchange, metal phase changes, distribution of temperatures in the mould, chemical composition of the metal, flow of water in the primary and secondary cooling system and the casting speed. Moreover, the algorithm permitted to predict the behaviour of the process variables in the continuous casting of steel according to its profile and type.

Key words: simulation, solidification, continuous casting, modelling.

---

 

 

INTRODUCCIÓN

El proceso de colada continua ha sido uno de los mayores avances en la producción del acero durante el último siglo. Esta tecnología comienza a extenderse en los años 60, pero es a partir de la década del 70 cuando su expansión es más pronunciada, reemplazando paulatinamente al método convencional de colado de lingotes.

Diversos autores [1] trabajan actualmente en la simulación de procesos metalúrgicos y en especial en el vaciado continuo. En la última década, debido a los elevados costes por concepto de energía, montaje, mantenimiento y explotación de instalaciones de vaciado continuo pilotos [2] se evidencia que la generación de tecnologías para el proceso de vaciado continuo resulta inconcebible sin la ayuda de procedimientos efectivos de simulación cuyos resultados coincidan con los experimentos prácticos. Este logro se traduce en un control eficiente del propio proceso.

Por lo antes expuesto, en este trabajo se diseña un algoritmo para simular el proceso de vaciado continuo en máquinas de tipo radial a partir de los complejos mecanismos de transferencia de calor acero-molde, cambio de fase del metal, distribución de temperaturas en el cristalizador, composición química del metal, flujo de agua en el enfriamiento primario y secundario. El objetivo del presente trabajo es modelar y simular el proceso de vaciado continuo en instalaciones de tipo radial utilizando el Método de los Elementos Finitos (MEF).

Para la obtención de un algoritmo a partir de un modelo matemático que represente un proceso, es necesario seguir una trayectoria desglosada en diferentes pasos [3]:

1. Definición del problema y sus objetivos.
2. Definición de la teoría que sustenta el problema.
3. Descripción de la situación física, si existe, en términos matemáticos.
4. Solución matemática del modelo.
5. Comparación del modelo con la situación real.
6. Estudio de las limitaciones del modelo.

Es posible además, adquirir una idea mucho más clara del estudio de cualquier proceso metalúrgico bajo un enfoque sistémico (Fig. 1), en él se resumen las ideas expresadas hasta el momento con relación a la modelación [4]. Para esto se parte de un análisis externo del fenómeno a estudiar y se descomponen las tareas a resolver más complejas en sub tareas más sencillas que se analizan internamente mediante el algoritmo expuesto.

Así, diversos autores utilizan esta estrategia para el modelado de los procesos que intervienen en el vaciado continuo del acero, realizando adecuaciones según los casos concretos estudiados. A continuación se exponen algunos de los resultados más relevantes. En el año 2006, investigadores de la Universidad de Timisoara, Rumania [5] crearon un algoritmo para la simulación de la solidificación del acero en instalaciones de vaciado de tipo radial. Este algoritmo se centra en el modelado del enfriamiento del acero en moldes a partir de técnicas heurísticas para generar soluciones aproximadas del frente de solidificación del acero líquido. La virtud de estos resultados radica en que se creó una tendencia a modelar el proceso de colada continua a partir de modelos matemáticos complejos.

En el estudio desarrollado por Barcos y otros en el año 2007 se presenta un novedoso método de simulación que resuelve el proceso en su conjunto, siendo las variables del proceso las condiciones de contomo y mediante la utilización conjunta de herramientas comerciales (FLUENT y ABAQUS) y una serie de modelos de desarrollo propio, resuelven las interacciones entre los distintos fenómenos físicos presentes en la colada continua de aceros de baja y media aleación. Lo más relevante de este trabajo es que a partir de su publicación se evidencia la necesidad de modelar el proceso a partir de herramientas numéricas.

Otra propuesta fue realizada en el año 2008 por especialistas de la Universidad de Barcelona [6], donde se obtiene un programa que simula el comportamiento durante la colada de otros materiales metálicos como el titanio. Para esto se apoyan en un modelo estocástico de la solidificación en tiempo real del metal en un molde fijo. De la misma manera profesores del departamento de Matemática aplicada de la Universidad de Massachusetts [7], crearon un prototipo virtual de Instalación de Vaciado Continuo (IVC) a partir del modelado de la velocidad de colada en función de la temperatura del metal vaciado. En el procedimiento expuesto, se obtuvo el modelado a partir de la distribución de las temperaturas a lo largo un cristalizador curvilíneo de cobre que utiliza agua tratada como medio refrigerante. Para obtener la distribución de temperaturas se colocó en la pared del molde termocouplas de última generación. Los resultados de esta investigación evidencian que las propiedades físicas se pueden considerar linealmente dependiente de la temperatura con un nivel de confianza del 96 por ciento.

Los autores de [8], en el año 2010, han utilizado la transferencia de calor durante el enfriamiento por zonas en instalaciones de tipo radial para estimar el coeficiente de termo transferencia mediante un modelo estadístico para la estimación del coeficiente global de transferencia de calor. Para esto, se desarrolla un modelo físico matemático considerando la transferencia de calor como estacionaria en las dos direcciones tangenciales a la dirección de colada. Estos resultados han sido validados a escala de planta piloto y se consideran pioneros en la utilización de técnicas de Neuronal NetWare aplicadas a la inteligencia artificial en procesos industriales.

Otros [9], también en el año 2010, modelan las fatigas térmicas durante el vaciado a partir de los mecanismos de trasmisión del calor en dos dimensiones. En su procedimiento se vierte plomo en polvo durante el vaciado y se expone las muestras obtenidos a un microscopio de barrido, determinando el frente de solidificación del metal en el molde. En este trabajo se cristalizan los primeros resultados teóricos de las investigaciones previas demostrando la dependencia semiparabólica del frente de solidificación y el tiempo.

La novedad de esta investigación, es la simulación del proceso de intercambio térmico durante la solidificación en el proceso de vaciado continuo de aceros al carbono de baja aleación.

 

MÉTODOS DE ANÁLISIS

En las instalaciones de vaciado continuo generalmente existen de 3 zonas, en ellas los procesos de transferencia de calor ocurren por diferentes mecanismos por lo que resulta conveniente separar el estudio en 3 partes. En estas zonas los mecanismos físicos de extracción del calor difieren bastante. La primera zona es la encargada de formar una capa sólida capaz de resistir la presión metalóstatica del acero líquido. En la segunda zona el metal alcanza su completa solidificación y en la tercera el metal homogeniza la estructura final del lingote.

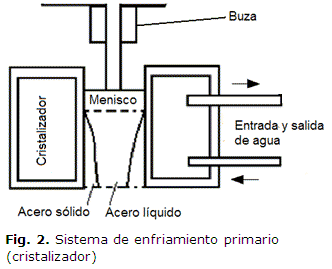
En la primera zona, el enfriamiento ocurre en el cristalizador o molde donde el metal alcanza la temperatura de sólidus en el frente de solidificación (Fig. 2). En esta zona, la transferencia térmica considera el problema como estacionario sin generación interna de calor.

Esto se debe a que generalmente se pretende estudiar el comportamiento estable del proceso y no sus etapas transitorias como un cambio de velocidad de colada, o el mismo arranque y llenado del molde.

La conducción de calor de un sistema estacionario, sin generación interna de calor, está definida por la ecuación diferencial:

Donde: Ω_molde, se adopta por convención como el dominio asociado a la función para una cara del molde, siendo válido el modelo para las demás caras. Las condiciones del modelo en el molde de palanquillas que se estudia se expresan a continuación.

Transferencia de calor por conducción en las paredes del molde

La transferencia de calor por conducción en el molde está determinada por la conductividad térmica del material. El fenómeno de solidificación en la palanquilla de acero puede estudiarse por medio de un modelo bidimensional de transferencia de calor con cambio de fase, la simplificación de este modelo es posible si se desprecia la conducción en la dirección de colada y se tratan los fenómenos de transporte convectivos en el acero por medio de una conductividad térmica efectiva. Aceptando estas simplificaciones, el dominio en estudio será la sección transversal de la palanquilla, Ω_acero, definido por el lado de la sección cuadrada del producto colado. Las condiciones de borde se muestran en la figura 3, estas están función del tiempo y asociadas a cada una de las zonas de refrigeración. La determinación del flujo de calor acero-molde en este proceso, necesario para definir la condición de borde en la frontera Ω_acero, es de gran complejidad tanto desde el punto de vista teórico como experimental.

En base a experiencias realizadas en un molde estático [10], se desarrolló la siguiente expresión:

Para la investigación es posible dividir el problema en 4 subsistemas debido a que la sección transversal de la palanquilla y las condiciones de enfriamiento son estrictamente idénticas en cada cuadrante por lo que basta resolver uno de ellos.

Donde t, es el tiempo de residencia del acero en el molde, en segundos. Para su estimación se considera que el proceso transcurre a velocidad constante durante intervalos prolongados. De esta consideración se obtiene:

t=Z/v (4)

Extracción de calor durante el enfriamiento secundario

La segunda zona es la de refrigeración por Sprays (Fig. 4). En ella, el metal semi-líquido posee una cáscara solidificada por lo que los mecanismos de transferencia de calor tienen en cuenta la convección forzada del agua calentada, el calor latente de solidificación del acero, la conducción en el sistema palanquilla-rodillos y la radiación térmica, entre otros. Sin embargo, no todos tienen la misma intensidad por lo que se pueden despreciar algunos para simplificar el modelo.

La extracción de calor durante el enfriamiento secundario, es una combinación de los siguientes fenómenos.

1. Transferencia de calor por acción directa del agua de refrigeración. Este es el principal mecanismo de extracción de calor durante el enfriamiento secundario y se ve afectado principalmente por el caudal específico de agua en los rociadores, W. El caudal específico es la cantidad de agua que impacta sobre el producto colado, por unidad de tiempo y por unidad de superficie.

2. Transferencia de calor por radiación. Sobre las superficies libres que no están en contacto con el agua de refrigeración, la extracción de calor se produce básicamente por radiación con el medio. Los coeficientes de emisividad utilizados oscilan entre 0.7 y 0.9, siendo el valor más utilizado 0.8. Todos estos mecanismos de extracción de calor pueden modelarse en forma integral:

Donde el coeficiente de transmisión superficial del calor (h_conv) se expresa en KW/m² ºC.

Siendo los coeficientes, según ajustes experimentales, [11] a = 1.57, b = 0.55, c = .0075, α = 4.

Donde: W se expresa en 1/m² seg y la temperatura del agua T_agua en ºC.

Transferencia de calor por convección con el agua de refrigeración

La transferencia de calor es modelada como un fenómeno de convección forzada con flujo totalmente desarrollado térmicamente dentro de un canal de paredes lisas, sin considerar la vaporización del agua de enfriamiento.

Siendo k_agua, ρ_agua, µ_agua, Cp_agua, V_agua, la conductividad térmica, la densidad, la viscosidad, el calor específico y la velocidad del agua, respectivamente; y D_h, el diámetro hidráulico del canal de refrigeración.

Generalmente sobre la superficie sobre la cual circula el agua se depositan sedimentos cuya resistencia puede llegar a reducir notablemente la transferencia de calor. Este fenómeno es considerado suponiendo un espesor de película, d_sed, y sumando una resistencia térmica al coeficiente de convección calculado en la ecuación 6.

Extracción de calor durante el enfriamiento terciario

Cuando el producto colado abandona la zona de enfriamiento secundario, los únicos mecanismos de extracción de calor son la radiación térmica y la convección libre con el medio ambiente:

Donde: h_aire es el coeficiente de transmisión superficial del calor, ε el grado de negrura del acero y σ la constante de Stefan- Boltzman.

Condiciones de del problema

Las condiciones iniciales y de borde del problema están definidas por:

Donde T_colada es la temperatura con que ingresa el acero líquido al molde. Los tiempos dependerán de la velocidad de colada utilizada y de la disposición de cada una de las zonas en la máquina de colada continua. Siendo x_nivel , el nivel de acero en el molde; x_molde, la longitud del molde; x_sec y x_ter la distancia al extremo superior del molde del comienzo y el fin de la zona de enfriamiento terciario.

Propiedades termo físicas del acero

Un aspecto importante a tener en cuenta, en modelos de solidificación de acero, es utilizar propiedades termo físicas adecuadas a la química real del acero Miettinen [12] ha desarrollado un algoritmo de cálculo para la determinación de las propiedades del acero durante su solidificación en función de la composición química. Utilizando este algoritmo se obtienen las temperaturas de transición y las propiedades termo físicas en cada una de las fases. Para el rango de temperatura utilizado durante el proceso de colada continua, se han adoptado valores constantes de las propiedades termo físicas en cada fase y una dependencia lineal de la temperatura en cada zona de transición:

Donde: Φ es una propiedad termo física genérica. El calor latente de cambio de fase es calculado, con el mismo algoritmo, teniéndose L_ls y L_ya para la transición "líquidus - sólidus" y "hierro-ϒ hierro-α", respectivamente.

Discretización por el Método de los Elementos Finitos (MEF)

El problema así planteado es resuelto por medio de un método de dominio fijo, con propiedades dependientes de la temperatura y con dos cambios de fases en los intervalos de temperaturas T_líquidus, T_sólidus, y Tⁱ_ya, T^f_ya. Utilizando el MEF se deberá resolver el siguiente problema iterativo:

Siendo:

Donde el primer sumando corresponde a la estimación del coeficiente de termo transferencia por convección forzada y el segundo corresponde a la conducción a través de la capa de metal solidificado.

La expresión 25 se obtiene tomando en consideración el balance térmico en la superficie de la palanquilla.

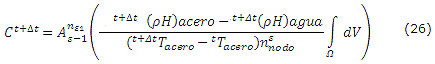
Donde: A, representa el operador ensamble de elementos y Hi^eq la función temporal definida como:

En la figura 5 se muestra el diagrama de bloques del método antes expuesto. Es recomendable y así se tiene en cuenta en el algoritmo; el uso de una cantidad de iteraciones suficientes hasta que no ocurra una mejora visible en el modelo simulado.

El algoritmo está compuesto por 3 partes funcionales. En la primera de ellas se estima de forma directa el coeficiente de transmisión total del calor a partir de las propiedades termo físicas del agua y del acero obtenidas a través de las ecuaciones criteriales a la temperatura deseada por cada zona de la instalación. También se obtiene los resultados previos la de extracción del calor por cada zona de la IVC.

En la segunda parte se le impone restricciones al modelo mediante las ecuaciones de sensibilidad para el MEF, considerando el problema simétrico y estacionario en la dirección de la extracción del calor y en la tercera se construye el modelo definitivo y se grafican los resultados.

Para la implementación del procedimiento se programó el algoritmo utilizando un lenguaje de programación con interface para un software de cálculo obteniéndose el Sistema para la Simulación del Proceso de Vaciado Continuo (SiSVAC). La figura 6 muestra la interface principal del programa, en ella se introducen los datos necesarios para el cálculo, dispone de una base de datos que reporta los parámetros físicos necesarios tales como el calor latente de solidificación, tipo de palanquilla a colar y densidad a la temperatura de vertido según la composición química. Una vez introducidos los datos se ejecuta el programa y el sistema muestra la ventana de resultados (Fig.7)

Esta ventana contiene dos pestañas. En la primera se obtienen los resultados de la solidificación del acero a lo largo de la instalación y a través del tiempo. Así mismo reporta la cantidad de agua necesaria por cada zona de la máquina de colada continua, el tiempo necesario para terminar el ciclo tecnológico y la distancia aproximada a la que se cierra el cono de solidificación. La segunda pestaña ofrece la misma información pero a partir de gráficos del proceso.

 

RESULTADOS Y DISCUSIÓN

Aplicación del algoritmo a un caso de estudio

Para la validación y posterior puesta en explotación de los resultados se utilizó la IVC de una Empresa Siderúrgica cubana para comparar los resultados obtenidos mediante la simulación y los datos reales reportados por la máquina.

• Esta instalación tiene las siguientes características:
• Máquina tipo 2BLC - 505.
• Cinco líneas de vaciado.
• Radio de curvatura: 5000 mm.
• Secciones de vaciado: cuadrado de 90 x 90, 100 x 100 y 130 x 130 mm.
• Velocidad de vaciado: 0.6 - 6 m/min.
• Constante metalúrgica (distancia entre centros de cristalizadores): 1000 mm.
• Largo metalúrgico: 14 m.

Datos de la instalación

Dentro de la tecnología de vaciado en la empresa se tienen las siguientes variables:

Variables de entrada:

Temperatura del agua a la salida del cristalizador

Composición química.

Velocidad de colada.

Temperatura de la artesa.

Caudal de agua.

Variables de coordinación:

Productividad de la máquina.

Marca de acero.

Variables de salida:

Calor extraído.

Espesor de la cáscara solidificada.

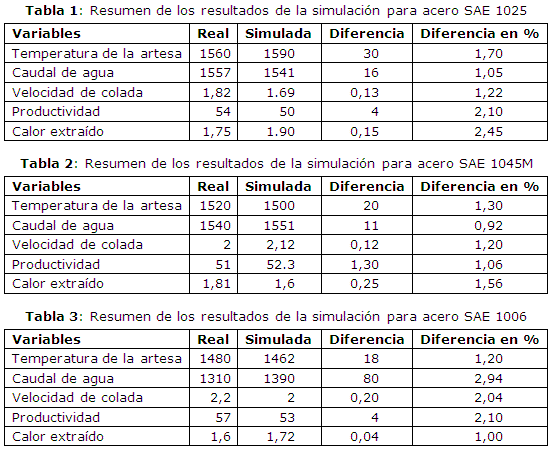
Desarrollada la simulación para aceros SAE 1025, SAE 1045 M y SAE 1006 respectivamente se obtuvo las variables implicadas en el proceso. Los resultados se resumen en las tablas 1, 2 y 3.

Como se puede observar en las tablas, la diferencia entre los valores obtenidos en el programa y los medidos en la instalación es insignificante, esto es debido a que la diferencia (error) entre los resultados nunca supera el 3 porciento, lo cual es admisible para resultados obtenidos por simulación.

La diferencia de los valores obtenidos en la medición de la temperatura del metal en la artesa oscila entre 18 y 30. Esto ocurre debido a que para la simulación se considera la temperatura del metal constante en todo el volumen del cuerpo. Por otra parte influye en menor medida la distancia a la que se sumerge la termocoupla en el baño metálico.

El comportamiento real del caudal de agua que fluye en los cristalizadores evidencia al compararse con los valores obtenidos mediante la simulación que el modelo de [10] es válido para estimar el caudal de agua en la tecnología de vaciado de aceros de baja aleación.

De todas las variables estudiadas la que menos variabilidad presenta es la velocidad de colada. Este resultado se evidencia en que los valores medidos y simulados están acotados entre 1.69 y 2.12 m/min. Estos valores ofrecen una medida cualitativa y cuantitativa de la veracidad del programa debido a que la velocidad de colada depende débilmente de las propiedades físicas y químicas del acero que se cuele.

Aunque la productividad de la máquina de vaciado continuo fluctúa dentro de los valores esperados, se denota una variabilidad apreciable entre los valores obtenidos por simulación y los medidos en la planta estudiada. La razón principal se centra en el posible error que se comete al considerar la densidad lineal del acero constante e independiente de la marca y la temperatura del acero que se manufactura. Sin embargo, se evidencia la proporción directa que existe entre el aumento de la productividad de la instalación con el aumento de la velocidad de vaciado por marca de acero durante la medición real y la simulación.

Además, los resultados evidencian que el modelo obtenido para la simulación se aleja más de los valores reales con el aumento del contenido de carbono en la aleación de acero. De todas las variables de decisión simuladas, la que más fluctúa dentro de los valores admisibles es el calor extraído al acero mediante el agua durante el enfriamiento primario. Esto ocurre debido a que se utilizan las fórmulas 19 y 20 para estimar algunas propiedades físicas del agua y el acero introduciendo un error extra en los cálculos. Otro factor a tener en cuenta es la perturbación inicial por concepto de choque térmico al ser vertido el acero en el molde.

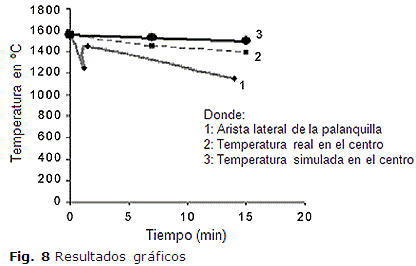
Finalmente, la figura 8, muestra comparativamente el comportamiento predictivo de la temperatura en función del tiempo. La curva 1 muestra el comportamiento de la temperatura en la arista de la palanquilla en La curva 2 y 3 se representa las temperaturas reales y simuladas respectivamente para un acero SAE 1025. Se realizó la medición de la temperatura en un solo acero para la validación debido a que el comportamiento de la misma no varía en marcas de acero de baja aleación sometidas al mismo proceso tecnológico.

 

CONCLUSIONES

-El algoritmo desarrollado permite, dentro de las condiciones simuladas estimar de forma asistida por computadora los parámetros controlados durante el vaciado continuo del acero así como los complejos mecanismos de transferencia de calor.

-El modelo permite predecir con suficiente pericia el comportamiento de las variables durante el proceso de vaciado continuo de acero según perfil y marca del mismo.

-El sistema estratifica el proceso de solidificación por cada zona de enfriamiento de la instalación lo cual es muy importante en el proceso tecnológico para la toma de decisiones.

-Las propiedades físicas simuladas concuerdan con la realidad dentro del error admisible provocado en la propia simulación.

-No se conoce si el algoritmo resulta factible para otros tipos de aceros.

 

REFERENCIAS

1. Heput,T. y Berciano, V. "Modelling and simulations of continuous casting steel". Revista de Metalurgia del CENIM, 2009. vol. 48, p 23-26. [Consultado el: 16 de octubre del 2011]. Disponible en: http://revistademetalurgia.revistas.csic.es/112323. ISSN 120-298X.

2. Zarka, J. Intelligent optimal design of complex systems. France: Editorial Wards systems, 2008, p. 265-269. ISBN 831-232-869-13.

3. Orrling, C. "Observations of the melting and solidification behavior of mold slags, Iron and Steelmaker". Journal of materials processing technology, 2000, vol. 27, nº. 1, p. 53-63, [Consultado el: 20 de junio del 2011]. Disponible en: http://www.sciencedirect.com/science/journal/0.95162x. ISSN 095-016-2X.

4. Habert, G. "A numerical model for a heat flux DSC: Determining heat transfer coefficients within a DSC". Ironmaking & Steelmaking. 2009, vol. 40, p. 12-16. [Consultado el: 2 de abril de 2011]. Disponible en: http://www.sciencedirect.com/science/journal/01691317. ISSN 016 91317.

5. Janik, M. y Dyja, H. "Modelling of three-dimensional temperature field inside the mould during continuous casting of steel". Computer methods in applieds mecanisc and engineering. 2009. vol. 10, p. 62-66, [Consultado el: 13 de enero del 2009]. Disponible en: http://www.elsevier.com/locate/jmatprotec/15315410. ISSN 153-154-10.

6. Incropera, F. Fundamentos de transferencia de calor. USA: Editorial Prentice Hall, 2010, p. 213-295. ISBN 970-17-017-04

7. Hardin, R. y Beckerman, C. "A transient simulation and dynamic spray cooling control model for continuous steel casting". Metallurgical and Material Transactions B. 2004. vol. 34B. p. 95 - 109. [Consultado el: 3 de julio del 2009]. Disponible en: http://www.elsevier.com/locate/jmatprotec/578582. ISSN 578 582

8. Viera, B. y Pereira, D. Modelación Matemática para Ingenieros Químicos. La Habana: Pueblo y Educación. 2010. ISBN 909-229-074-00

9. Solorio, K. "Simulation of continuous cast steel product solidification", Revista de Metalurgia del CENIM. 2007. vol. 43, p 3-8. [Consultado el: 2 de mayo del 2010]. Disponible en: http://revistademetalurgia.revistas.csic.es/120298. ISSN 120-298X.

10. Isachenko V, Transferencia de calor. 6a ed. Moscú: Editorial MIR, 1989, p. 145-156. ISBN 282-007-128

11. Meng, Y. "Application of a heuristic search technique for the improvement of spray zones cooling conditions in continuously cast steel billets". Metallurgical and Material Transactions B. 2004. vol. 34B. p. 95-109. [Consultado el: 6 de agosto del 2010]. Disponible en: http://www.elsevier.com/locate/apm/104115. ISSN 104-115.

12. Miettinen, K. "Flow control technology from converter to mould". Metallurgical Plant and technology. 2011, vol. 2, p. 32-34. ISSN 0935-7254.

 

 

Recibido: 12 de junio de 2012.
Aceptado: 4 de septiembre de 2012.

 

 

Yusdel Díaz Hernández. Instituto Superior Politécnico José Antonio Echeverría. Facultad de Ingeniería Mecánica. La Habana. Cuba.
Correo electrónico: [e-mail]