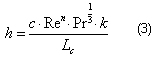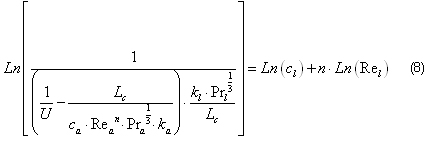ARTÍCULO ORIGINAL

 

Coeficientes de transferencia de calor experimental para el enfriamiento de licor en intercambiadores de placas

 

Experimental heat transfer coefficients for the liquor cooling in plate heat exchanger

 

 

Enrique Torres-Tamayo, Yoalbys Retirado-Medianeja, Ever Góngora-Leyva

Instituto Superior Minero Metalúrgico. Centro de Estudio de Energía y Tecnología Avanzada de Moa. Holguín. Cuba

 

 

---

RESUMEN

La pérdida de eficiencia del proceso de enfriamiento del licor amoniacal, mediante el uso de intercambiadores de calor de placas, está asociada a imprecisiones en la estimación de los coeficientes de transferencia de calor y la acumulación de incrustaciones en la superficie de intercambio. El objetivo de la investigación es determinar los coeficientes de transferencia de calor y la influencia de las incrustaciones en la pérdida de eficiencia de la instalación. Mediante un procedimiento iterativo se estableció la ecuación del número de Nusselt y su relación con el número de Reynolds y Prandtl. Se utilizó un diseño experimental multifactorial. Los resultados predicen el conocimiento de los coeficientes para el cálculo del número de Nusselt en ambos fluidos. Los valores de los coeficientes del licor amoniacal son inferiores, ello se debe a la presencia de componentes gaseosos. La ecuación obtenida muestra correspondencia con el modelo de Buonapane, el error comparativo es del 3,55 %.

Palabras claves: intercambiador de calor de placas, coeficientes de transferencia de calor, eficiencia térmica.

---

ABSTRACT

The loss of efficiency of the ammonia liquor cooling process, by means of the plate heat exchanger, is associated to the incorrect estimate of the heat transfer coefficients and the accumulation of inlays in the exchange surface. The objective of the investigation is to determine the transfer coefficients and the influence of the inlays in the efficiency loss of the installation. By means of an iterative procedure was obtained the Nusselt number equation and the relationship with the Reynolds and Prandtl number, for it was used it a design experimental multifactorial. The results predict the knowledge of the coefficients for the calculation of the Nusselt number for both fluids. The ammonia liquor coefficients values are inferior, due to the presence of gassy components. The obtained equation shows correspondence with the Buonapane pattern, the comparative error is 3,55 %.

Key words: plate heat exchanger, heat transfer coefficients, thermal efficiency.

---

 

INTRODUCCIÓN

Los procesos de intercambio de calor entre dos fluidos que están a diferentes temperaturas y separados por una pared sólida ocurren en muchas aplicaciones de las empresas productoras de níquel. El dispositivo que se utiliza para llevar a cabo este proceso se denomina intercambiador de calor. En la Unidad Básica de producción Lixiviación se produce el enfriamiento del licor amoniacal con el fin de facilitar el proceso de lixiviado de la pulpa laterítica. Los intercambiadores de calor de placas, en comparación con los de carcasa y tubos, son los más eficientes siempre que la diferencia de temperatura entre ambas corrientes fluidas sea baja. Logran una alta eficiencia gracias a la gran superficie de intercambio que existe entre los dos fluidos, ellos circulan por canales muy estrechos en los que es posible incrementar la superficie de contacto, pero en cambio presentan problemas de incrustaciones y elevada pérdida de carga debido al uso de fluidos incrustantes (licor amoniacal). Lo anterior ha motivado el desarrollo de la presente investigación, con el objetivo de determinar los coeficientes de transferencia en intercambiadores de calor de placas y la influencia de las incrustaciones en la pérdida de eficiencia de la instalación.

En la determinación de los coeficientes de transferencia de calor y la eficiencia térmica de un intercambiador es necesaria la integración de varios conceptos de termotecnia y dinámica de los fluidos, y buena parte está dada por consideraciones experimentales. Estos coeficientes se definen en términos de la resistencia térmica total para la transferencia de calor entre dos fluidos, ello incluye las resistencias por convección y conducción para superficies planas o cilíndricas [6, 7, 12]. Los coeficientes de transferencia de calor, obtenidos de forma experimental, para diferentes aplicaciones se exponen en la literatura consultada [3, 5]. Los autores resumen las técnicas experimentales usadas para obtener los coeficientes y su dependencia de diferentes números adimensionales: Nusselt, Reynolds y Prandtl. En todos los casos los resultados son aplicables a las condiciones específicas en que se desarrollaron los experimentos, por lo que en escenarios diferentes es necesario comprobaciones experimentales que permitan determinar la aplicabilidad de los resultados.

Existen varios trabajos de investigación desarrollados con el fin de obtener los coeficientes de transferencia de calor mediante el uso de métodos numéricos y técnicas computacionales [1, 4, 10], en general se obtienen simulaciones que permiten predecir el comportamiento de las variables en intercambiadores de calor de placas para diferentes condiciones de operación. La obtención de modelos matemáticos y el empleo de métodos de optimización son usados por varios investigadores [2, 9, 11], los que permiten el análisis de los parámetros geométricos, ángulos de las placas, y el impacto en el diseño de los intercambiadores de calor.

El análisis de los trabajos precedentes demuestra la necesidad de usar resultados experimentales en la estimación de los coeficientes de transferencia en intercambiadores de calor, los errores que se comenten en la selección y evaluación de las instalaciones son menores y permiten predecir la dependencia de los coeficientes con los números adimensionales: Nusselt, Reynolds y Prandtl.

 

MÉTODOS Y MATERIALES

Mediante el uso de los coeficientes de transferencia de calor por convección para ambos fluidos y el conocimiento de las resistencias por incrustaciones, el coeficiente global de transferencia de calor se obtiene por la siguiente expresión [7]:

El valor del coeficiente global (U) depende de los coeficientes de transferencia de calor por convección de los fluidos frío y caliente (h_l, h_a) y está fuertemente influenciado por la forma de las corrugaciones de las placas, los parámetros de trabajo y las propiedades de los fluidos. Investigaciones anteriores [13, 14] han reportado el procedimiento para la obtención de los coeficientes con fluidos de características diferentes, se plantea la necesidad de obtener los mismos de forma experimental cuando no existe referencia en la literatura, debido a los errores que se cometen en la selección de los equipos de intercambio térmico.

Las resistencias térmicas de ensuciamiento (R_l, R_a) se generan como consecuencia de que los fluidos pueden transportar contaminantes, y con el paso del tiempo estos se van depositando sobre las superficies. De este modo se crea una capa entre el fluido y la superficie que crece en espesor y genera una resistencia térmica adicional con un valor significativo para el cálculo del coeficiente global de transferencia de calor.

Debido a que las placas están construidas de acero inoxidable AISI 316, cuya conductividad térmica (k_m) es de 13,4 W/mK, se tiene que para el espesor de placa (e) de 0,4 mm, la resistencia de conducción es [8]:

Las resistencias de conducción y por incrustaciones de las placas, cuando se realiza la limpieza del intercambiador de calor, son despreciables en comparación con las de convección para ambos fluidos. Para el cálculo de los coeficientes de convección es necesario establecer su relación con números adimensionales tales como: Reynolds (Re), Nusselt (Nu), Prantdl (Pr). Su forma general se puede expresar por la siguiente ecuación [7].

Los valores de los coeficientes c y n se obtienen de forma experimental y dependen del tipo de flujo y. La longitud característica del canal (L_c), luego de algunas transformaciones, se determina por la siguiente expresión: L_c=2.b

Donde:

k: conductividad térmica del fluido; W/m·K.

b: ancho del canal o distancia entre placas; m.

Procedimiento de cálculo

Para calcular el valor de los coeficientes n, c_l, c_a se aplica un procedimiento a partir del cual los resultados experimentales convergen, se ha dispuesto la misma dependencia del número de Nusselt con el de Reynolds para ambos lados del intercambiador debido a que se tiene una misma geometría. Sin embargo se toman diferentes coeficientes para que absorban el efecto diferencial de las incrustaciones. Los coeficientes cl, ca se obtienen asumiendo un valor inicial del exponente n, ya que la ecuación 4 presenta la forma de la ecuación de una recta, ecuación 5.

 

Donde:

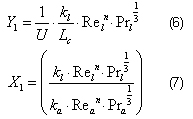
Para conseguir que los valores converjan es necesaria la obtención de una nueva ecuación, luego de algunas transformaciones a la expresión 1 y utilizando las propiedades de los logaritmos se obtiene:

Al igual que la ecuación 4 esta nueva expresión presenta la forma de la ecuación de una recta. Con los valores de c_l, c_a obtenidos en la expresión 4, se introducen en la ecuación 8 de forma que se obtiene un nuevo valor de "n". Mediante el uso de un proceso iterativo, y el uso del software profesional MATHCAD 13, es posible la convergencia del método de cálculo.

Donde:

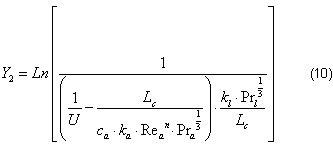
Eficiencia e incrustaciones de los intercambiadores de calor de placas

La influencia de las incrustaciones en la pérdida de eficiencia de los intercambiadores de calor se determinó mediante el coeficiente global de transferencia de calor en función de los parámetros de entrada y salida del equipo [15].

El factor de incrustaciones (R_d) se obtiene mediante la comparación del valor del coeficiente global de transferencia de calor, obtenido de forma experimental cuando el equipo está limpio (U_máx, con los valores experimentales de la ecuación 12 en función del tiempo.

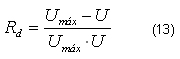
La eficiencia es el porcentaje que representa la relación del desempeño real del equipo con respecto al desempeño máximo

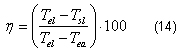
Técnica experimental

De acuerdo con el procedimiento de cálculo establecido, las principales variables involucradas en el proceso de enfriamiento del licor amoniacal en la U.B.P. Lixiviación de la empresa niquelífera son las siguientes:

• Temperatura de entrada del licor amoniacal y agua de enfriamiento
• Temperatura de salida del licor amoniacal y agua de enfriamiento
• Flujo másico del licor amoniacal y agua de enfriamiento
• Presión de entrada y salida del licor amoniacal y agua de enfriamiento

Los experimentos, para determinar los coeficientes de transferencia de calor, se efectuaron fijando dos variables: el flujo másico de agua y el flujo másico del licor amoniacal, el resto de las variables se consideraron aleatorias. Los niveles de cada variable se obtuvieron a partir de los parámetros de trabajo del proceso de enfriamiento del licor amoniacal en la empresa "Comandante Ernesto Che Guevara". El intercambiador de calor de placas usado en la experimentación se encuentra instalado en el propio proceso productivo, ello permitió garantizar la semejanza geométrica. El área de intercambio térmico es de 589 m² y las placas usadas son del tipo Chevron.

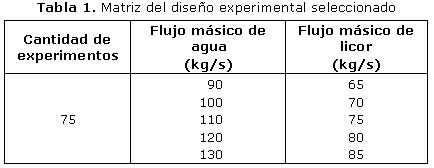
El número de corridas experimentales se obtuvo mediante un diseño multifactorial, de acuerdo con los niveles prefijados de cada una de las variables suma un número de 25; pero con el objetivo de comprobar la validez de los experimentos y disminuir los errores de observación, en todos los niveles se efectuaron 3 réplicas, lo que concluye con un total de 75 corridas experimentales. En la tabla 1 se muestra un resumen del diseño experimental efectuado.

La influencia de las incrustaciones en la pérdida de eficiencia de los intercambiadores de placas durante el enfriamiento del licor amoniacal se determinó mediante cinco corridas experimentales, el tiempo de duración fue de 109 días. Antes de cada experimento se realizó la limpieza del sistema mediante el desarme y el uso de los productos químicos apropiados para estos casos.

Características del licor amoniacal

El licor amoniacal es un líquido de color azul prusia con las siguientes características:

• Densidad= 1,026 g/l
• Temperatura= 42 ºC
• Porciento de níquel = 11 g/l
• Porciento de cobalto = 0,4 g/l
• Porciento de amoniaco = 73 g/l
• Porciento dióxido de carbono = 34 g/l
• Sólidos ≤ 120 p

 

RESULTADOS Y DISCUSIÓN

Los resultados experimentales de las variables medidas en el intercambiador de placas, para determinar los coeficientes de transferencia de calor por convección, se exponen en la tabla 2. En todos los casos se confirma que la dispersión entre los resultados obtenidos no es significativa, encontrándose el error estándar de la media aritmética por debajo del 5 %.

Resultados de los coeficientes

Los valores de n, c_l, c_a se determinaron mediante un proceso iterativo usando el software profesional Mathcad 13, los resultados experimentales mostrados en la tabla 2 y el procedimiento de cálculo (ecuaciones 4 a la 11). Los valores de los coeficientes obtenidos son los siguientes: n=0,657; c_a=0,2883; c_l=0,2791. La estimación correcta de los coeficientes evita errores en el diseño de las instalaciones térmicas y la pérdida de capacidad en el proceso de intercambio térmico. El análisis del coeficiente global y su dependencia de los coeficientes de transferencia de calor por convección para el licor amoniacal y el agua, se expresa a través del número de Nusselt y los coeficientes n, c_l, c_a obtenidos.

Resultado del número de Nusselt para el agua.

Resultado del número de Nusselt para el licor amoniacal

La figura 1 muestra el comportamiento del número de Nusselt en función del Reynolds para los fluidos que intervienen en el proceso de intercambio térmico (licor amoniacal y agua). Se observa un incremento de los valores de Nusselt con el aumento del número de Reynolds, ello está asociado al incremento de la velocidad del fluido por el interior de los canales del intercambiador de placas y con ello un incremento de la turbulencia que favorece la transferencia de calor entre ambas corrientes fluidas. Los valores de Nusselt del agua son mayores que los obtenidos con el licor amoniacal, ello se debe a la presencia de componentes gaseosos en el licor que reducen el coeficiente de transferencia de calor por convección.

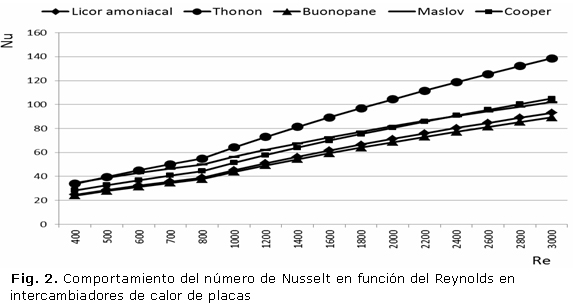
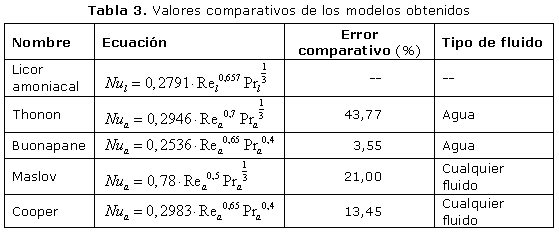
En la figura 2 se expone el comportamiento del número de Nusselt en función del Reynolds en intercambiadores de calor de placas según el criterio de varios investigadores [17] y el obtenido en este trabajo señalado con el nombre de "Licor amoniacal" en la gráfica. El modelo de Buonopane presenta un comportamiento similar al obtenido en esta investigación con un error comparativo del 3,55 %.

Los resultados obtenidos por Thonon y Maslov se alejan de los aquí presentados con valores superiores de los coeficientes de transferencia de calor y un error comparativo superior al 20 % por lo que no es recomendable el empleo de esos resultados en los cálculos ingenieriles para la selección y evaluación de instalaciones térmicas en la industria del níquel con el uso de intercambiadores de calor de placas. En la tabla 3 se exponen los modelos y el porciento de error comparativo con los resultados del licor amoniacal.

Resultados de la pérdida de eficiencia en el intercambiador de calor de placas

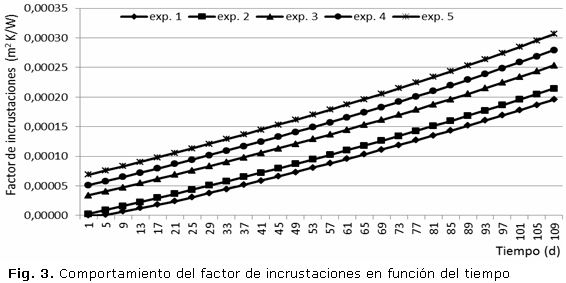
El comportamiento del factor se expone en la figura 3. Se observa tendencia al incremento, alcanzando valores que sobrepasan los 0,00025 m²K/W. Es necesario prestar atención al incremento del factor luego de la limpieza, ello debe estar asociado a la existencia de partículas incrustadas en las placas que provocan la pérdida de capacidad y de eficiencia del proceso de enfriamiento del licor amoniacal. Los resultados obtenidos en la presente investigación recomiendan la selección de valores elevados del factor (cercanos a 0,0002 m²K/W) para garantizar el diseño racional de instalaciones de intercambio térmico que usen fluidos con características similares al estudiado.

En la figura 4 se muestra el comportamiento de la eficiencia en función del tiempo. Los resultados exponen tendencias a la reducción de la eficiencia con el incremento del tiempo de trabajo de la instalación. Los requerimientos del proceso establecen mantener la temperatura de salida del licor amoniacal por debajo de 30 ºC, ello se logra cuando la eficiencia térmica es superior al 70 %. El tiempo indicado para la limpieza del equipo es de 105 días de funcionamiento continuo. Los resultados obtenido son aplicables solo para fluidos con características similares al estudiado en la investigación (licor amoniacal), para otros fluidos es necesario establecer el historial de comportamiento de las instalaciones, propósito que se desarrolla con el fin de minimizar los errores que se comenten en la selección y explotación de las instalaciones de intercambio térmico en la industria del níquel.

 

CONCLUSIONES

Los valores de los coeficientes son los siguientes: n=0,657; ca=0,2883; cl=0,2817. Ellos permiten el cálculo del número de Nusselt y el coeficiente global de transferencia de calor para el enfriamiento del licor amoniacal y fluidos de similares características en las empresas del níquel.

El incremento de las incrustaciones en función del tiempo de explotación de la instalación determina la reducción de la eficiencia. Los máximos valores se encuentran cercanos a 90 % y los mínimos se localizan en 70 % para tiempos de explotación de 105 días, por lo que se recomienda la limpieza y mantenimiento de los equipos de intercambio térmico en este período.

 

REFERENCIAS

1. Ahmed, F. y Mahmoud Sh. "Numerical analysis of fin-tube plate heat exchanger by using CFD technique. ARPN". Journal of Engineering and Applied Sciences. 2011, vol. 6, nº.7, p. 1-12. ISSN 1819-6608.

2. Amala, M., kum, S. y Muthuraman, S. "The characteristics of brazed plate heat exchangers with different chevron angles". Journal of Engineering and Applied Sciences. 2009, vol. 4, nº.10, p. 19-26. ISSN 1819-6608.

3. Constantinescu, D. y Petran, H. "Assessment of real heat transfer coefficients through shell and tube and plate heat exchangers". Journal of Civil Engineering Research. 2011, vol. 11, nº.1, p. 10-17. ISSN 1934-7359.

4. Dang, T. y Teng. J. "Numerical and experimental studies of the impact of flow arrangement on the behavior of heat transfer of a microchannel heat exchanger". Journal of Applied Mathematics. 2010, vol. 40, nº. 3, p. 1-7. ISSN 2152-7385.

5. Dayal, Sh. y Nema. V. "Experimental investigation of heat transfer and friction factor in a corrugated plate heat exchanger". Journal of Energy and Environment. 2011, vol. 2, nº.2, p. 287-296. ISSN 2076-2895.

6. Haghshenas, M., Talaie, M. y Nasr. S. "Numerical and experimental investigation of heat transfer of ZnO/water nanofluid in the concentric tube and plate heat exchangers". Journal of Thermal Science. 2011, vol. 15, nº.1, p. 183-194. ISSN 2334-7163.

7. Incropera, F. P. y David, P. W. Fundamentals of Heat and Mass Transfer. New York, U.S.A.: John Wiley & Sons. 2011.

8. Izquierdo M. Intercambiadores de calor de placas. Madrid, España: Departamento de Ingeniería Térmica y de Fluidos, Universidad de Carlos Tercero. 2002. p. 1-23. ISBN 3-540-21423-2.

9. Kaduchová, K. R. y Lenhard J. J. Optimization of heat exchanger for indirectly heated water heater. EPJ Web of Conferences, 2012, p. 1-10. [Consultado el: 10 de junio de 2012] Disponible en: http://www.epj-conferences.org/articles/epjconf/abs/2012/07/epjconf_EFM2011_01036 /epjconf_EFM2011_01036.html. DOI http://dx.doi.org/10.1051/epjconf/20122501036

10. Mohajeri, P. "A numerical comparison of single-phase forced convective heat transfer between round tube and straight microchannel heat exchangers". International Journal of Engineering Science and Technology. 2010, vol. 2, nº.11, p. 6492-6463. ISSN 0975-5462.

11. Pinto, J. M. y Gut, J. "A screening method for the optimal selection of plate heat exchanger configurations". Brazilian Journal of Chemical Engineering, 2002, vol. 19, nº. 4, p. 433 - 439. ISSN 0104-6632.

12. Reyes A., Toledo, M., Quinto, P. et al. "The Design of Heat Exchangers". Journal of Engineering, 2011. vol. 3, nº.1, p. 911-920. [Consultado el: 20 de junio de 2012]. Disponible en: http://www.SciRP.org/journal/eng. ISSN 0191-1920.

13. Selvaraj, P., Sarangan J. y Suresh, S. "Experimental investigation on heat transfer and friction factor characteristics of a water and ethylene glycol mixture flow of internally grooved tubes". International Journal of Chemical Research. 2011, vol. 3, nº.1, p. 33-40. [Consultado el: 20 de junio de 2012]. Disponible en: http://www.bioinfo.in/contents.php. ISSN 0975-3699.

14. Torres, E., Quintana, L., y Vega Y. R. "Coeficientes de transferencia de calor y pérdida de eficiencia en intercambiadores de calor de placas durante el enfriamiento del licor amoniacal". Minería y Geología, 2011, vol. 27, nº. 2, p. 67- 83. ISSN 1993-8012.

15. Varona, B. R., González, R. W. y Pérez. M. "Análisis del intercambiador de calor de placas enfriador de mosto en la cervecería Tínima". Tecnología Química, 2007, vol. 27, nº. 3, p. 61- 67. ISSN 2224-6185.

16. Zahid H. Plate Heat Exchanger Literature Survey and New Heat Transfer and Pressure Drop Correlations for Refrigerant Evaporators. New York, U.S.A: Wiley & Sons. 2003. ISBN 0-471-39015-1.

17. Zivkovic, E. S. y Kabelac S. S. "Local heat transfer coefficients during the evaporation of 1,1,1,2-tetrafluoroethane (R-134a) in a plate heat exchanger". Journal of the Serbian Chemical Society. 2008, vol.74, nº.4, p. 427-440. ISSN 0191-1840.

 

 

Recibido: 21 de junio de 2013.
Aceptado: 16 de octubre de 2013.

 

 

Enrique Torres-Tamayo. Instituto Superior Minero Metalúrgico. Centro de Estudio de Energía y Tecnología Avanzada de Moa.
Holguín. Cuba. Correo electrónico: [e-mail]