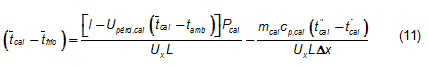Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.19 no.1 La Habana ene.-abr. 2016
ARTÍCULO ORIGINAL
Modelación matemática de un colector solar de tubos evacuados todo cristal
Mathematical modeling of an all glass evacuated tube solar collector
César Cisneros-RamírezI, Celso Recalde-MorenoII
I Instituto Superior Politécnico José Antonio Echeverría, Facultad de Ingeniería Mecánica. La Habana, Cuba
II Universidad Nacional de Chimborazo. Riobamba, Ecuador
RESUMEN
El trabajo trata sobre la modelación matemática de un colector solar de tubos evacuados todo cristal. En el desarrollo se obtuvo una ecuación para la evaluación del flujo termosifónico que se estableció en un colector de este tipo bajo la influencia de la radiación solar y como particularidad es que esta ecuación tiene en cuenta la relación de áreas que ocupa tanto el flujo caliente y el flujo frío que se establece en el colector. Como resultado se da el valor del flujo que se establece en función del ángulo de inclinación del colector y de la relación longitud/diámetro del tubo.
Palabras claves: colector, termosifón, modelo matemático, energía solar.
ABSTRACT
This paper deals with the mathematical modeling of an all glass evacuated solar collector. It was obtained an equation to evaluate the flow produced by the effect of the solar radiation on the tube.The equation takes into a count the flow area occupied by the hot fluid and the cool fluid besides the tilt angle and ratio length/diameter of the tube of solar collector.
Key words: collector, thermosy phon, mathematical model, solar energy.
INTRODUCCIÓN
Son varios los trabajos relacionados con el estudio del comportamiento de colectores solares de tubos evacuados todo cristal (CTETC) trabajando en régimen termosifón y en régimen forzado donde se combinan tanto la convección natural y la forzada. Una revisión de los trabajos desarrollados en esta temática lleva a dividir a los mismos en trabajos relacionados con la convección natural, trabajos relacionados con flujo forzado, trabajos relacionados tanto con convección natural como forzada, trabajos de simulación y trabajos experimentales.
Entre los trabajos relacionados con la convección natural se encuentra el realizado en [1] donde se realiza un estudio del comportamiento de un colector solar de tubos evacuado todo cristal (CTETC), para diferentes ángulos de inclinación los cuales coinciden para latitud media y alta (> = 20o). También en el trabajo [2] se realiza un estudio sobre el efecto del ángulo de inclinación en el comportamiento de un colector trabajando con aire donde el ángulo de inclinación fue variado entre 30 y 45 grados. En [3] el trabajo se centró en evaluar el comportamiento del CTETC trabajando con reflectores y nanofluido (agua - Al2O3) resultando un mejoramiento de la eficiencia en un 7,04 % y 16,9 % cuando se emplea reflector plano y curvo respectivamente. También se logró un mejoramiento con el empleo de nanofluido. El ángulo de inclinación de trabajo fue de 41o.El trabajo [4] se centró en el estudio de un colector CTETC para el calentamiento de aire y el ángulo de trabajo fue de 15o.
De los trabajos con flujo forzado se tiene el trabajo [5] cuyo objetivo fue establecer un modelo de transferencia de calor para un CTETC trabajando en régimen forzado. El modelo establecido tiene en cuenta la influencia de la convección natural. En [6] se realizó un estudio comparativo entre un CTETC y un colector de tubos en U. La comparación se realizó teniendo en cuenta la masa de fluido de cada colector lo cual arrojó que el colector de tubos en U tiene mejor eficiencia que el CTETC. El ángulo de inclinación definido en la investigación fue 60o.
En [7] el objetivo fue evaluar el comportamiento de un colector de tubos evacuado con tubos en U trabajando con pequeña concentración y sin concentración. Su conclusión fue que para sistemas domésticos es más eficiente el sistema sin concentración. Otros trabajos son relacionados a la simulación numérica de colectores [8, 9 ]
Del análisis anterior se aprecia que muchos aspectos del comportamiento termohidráulico de los colectores aún están siendo investigados y que a demás estas investigaciones están muy enmarcadas para latitudes medias y altas (> = 20º). Otro aspecto visto en el análisis es que los modelos que se han establecido tienen en cuenta la igualdad de área de flujo para el fluido caliente y para el fluido frío.
Por tanto, el presente trabajo tiene por objetivo la modelación de un colector solar de tubos evacuados todo cristal donde se tiene en cuenta la no uniformidad del área de flujo del fluido caliente y el fluido frío y además ángulo de inclinación del colector menores a 20º.
MÉTODOS Y MATERIALES
La figura 1 muestra el esquema del calentador a modelar. Para la modelación se considera el comportamiento térmico del colectora partir de un balance de energía donde se contemplan la ganancia y pérdida de energía en el mismo.
De las ecuaciones de conservación de la energía y del flujo se puede determinar el flujo originado por la circulación natural (ṁ) a través del tubo evacuado en un calentador solar a partir la energía colectada en el tubo, la temperatura inicial y la temperatura final en el tiempo de monitoreo [5, 10 ], ecuación 1
Donde
Donde G es la radiación incidente sobre el colector, Ac es el área de captación del colector, m es la masa del agua en el tubo (2,5 kg), los subíndices 1 y 2 indican el inicio y el final del monitoreo, t3 es la temperatura en la parte superior del tubo y tamb temperatura ambiente.
La ecuación para el cálculo del flujo termosifónico, se basa en considerar igualdad de área de flujo tanto para el fluido caliente como para el fluido frío. En [11] se llevó a cabo el desarrollo del proceso de transferencia de calor en un tubo inclinado calentado desde su extremo inferior y con los laterales adiabáticos. En dicho estudio se consideró además igualdad de sección de flujo para el fluido caliente y el fluido frío. En [5] este análisis se desarrolló considerando calor constante por los laterales del tubo e igual sección de flujo para las corrientes caliente y fría y además se tuvo en cuenta la combinación de convección natural y forzada.
En este trabajo a diferencia del de [5] y de [11] se desarrolla el modelo para el caso en que por los laterales del tubo se recibe calor constante proveniente del sol y además los fluidos caliente y frío no circulan por igual sección de flujo. La figura 2 muestra el volumen de control del tubo colector con inclinación respecto a la vertical y el balance de fuerza y energía.
Las suposiciones realizadas en este análisis son las siguientes:
· Flujo laminar desarrollado y régimen estacionario.
· Flujo newtoniano
· Propiedades constantes excepto la densidad.
· El tope inferior del tubo es adiabático
· El gradiente de presión del fluido caliente y del fluido frío son iguales  . De ser diferentes, entonces existiría flujo en la dirección transversal.
. De ser diferentes, entonces existiría flujo en la dirección transversal.
· Se desprecia la conducción del calor en la dirección del movimiento del fluido.
Para el diferencial del tubo dx el agua caliente aumenta su temperatura en tcal + dtcal y el agua fría aumenta su temperatura tfrio + dtfrio. Entre ambas corrientes ocurre transferencia de calor.
El balance de energía para cada corriente es (ver figura 2):
Para la corriente caliente
Para la corriente fría
En las ecuaciones anteriores q, qx y qperd son la energía incidente en la parte superior del tubo, el calor intercambiado entre las corrientes y el calor perdido al exterior por cada corriente, respectivamente.
El cálculo del calor absorbido y el intercambiado entre las corrientes se determina a partir de las ecuaciones 5 y 6
Donde tcal y tfrio son las temperaturas promedio de cada corriente y L es el valor de la cuerda de contacto entre la corriente caliente y la fría, figura 3
La pérdida de calor se determina a través de las ecuaciones 7 y 8
Donde Pcal y Pfrio son el perímetro cubierto por el fluido caliente y el frío respectivamente.
Para el análisis se tomó el mismo valor del coeficiente de traspaso de calor de pérdidas al ambiente, UI para ambas corrientes, o sea UI,cal = UI,frio = UI . El término Ux es el coeficiente de traspaso de calor entre las corrientes caliente y fría y se determina en función de los coeficientes peliculares de traspaso de calor hcal y hfrio de la corriente caliente y fría respectivamente.
Para el análisis del flujo termosifónico que se establece en el tubo es necesario recurrir a la ecuación del momentun la cual está basada en la 2da ley de Newton. La figura 2 muestra las fuerzas actuando sobre el volumen de control del fluido caliente y del fluido frío. Del balance de fuerzas y no considerando cambio de momentun en la dirección x, resulta la ecuación .
Donde fcal y ffrio son el área de flujo del fluido caliente y frío respectivamente. Pcal y Pfrio son el perímetro húmedo total del fluido caliente y frío respectivamente, los cuales se determinan según la figura 3, donde ε es la relación entre la parte cubierta por el fluido caliente y la parte cubierta por el fluido frío, o lo que es lo mismo ![]() , ver figura 3.
, ver figura 3.
En la ecuación 9 Twcal y Twfrio es la fricción. Esta fricción se puede determinar según [12], por la ecuación ![]() . Para el caso de flujo laminar el factor de fricción promedio ξ se determina en función del número de Reynolds según la ecuación
. Para el caso de flujo laminar el factor de fricción promedio ξ se determina en función del número de Reynolds según la ecuación ![]() , donde C es una constante. La dimensión característica en el número de Reynolds es el diámetro hidráulico determinado según [12, 13 ] por la ecuación
, donde C es una constante. La dimensión característica en el número de Reynolds es el diámetro hidráulico determinado según [12, 13 ] por la ecuación ![]()
Trabajando con las ecuaciones de τ , ξ y dh se obtiene la fricción a través de la ecuación 10 . En esta ecuación P*, f, νy m son el perímetro húmedo, área de flujo, viscosidad cinemática y flujo del fluido caliente o frío.
La diferencia de temperatura (tcal - tfrio) en la ecuación se puede determinar a partir de las ecuaciones 3 - 8, resultando la ecuación
Sustituyendo la ecuación en la ecuación y considerando la ecuación se llega a la ecuación para la determinación del flujo de fluido.
Donde:

Parámetro que tiene en cuenta el aumento en temperatura del fluido para una radiación incidente determinada.

Parámetro que tiene en cuenta la relación entre la región ocupada por el fluido caliente y el fluido frío.
La ecuación da la relación entre el flujo creado y la radiación incidente. Una de las simplificaciones para el desarrollo de esta ecuación es que el régimen de flujo es laminar y desarrollado. Para este caso el valor de los coeficientes peliculares de traspaso de calor se determinan para un valor de Nusselt constante (Un = 4,36), bajo condición de contorno de calor constante [13]. Además, considerando que ambos coeficientes peliculares son similares en magnitud, entonces el coeficiente global entre ambas corrientes se puede evaluar con la ecuación
El coeficiente de pérdidas de un tubo al vacío puede tomarse de un valor de 0,85 W/m2K, valor característico para estos tubos [14].
RESULTADOS Y DISCUSIÓN
Bajo las consideraciones realizadas, en la figuras 4 y 5 se presenta el resultado de la aplicación de la ecuación para el cálculo del flujo termosifónico.
Para el análisis del comportamiento del flujo termosifónico se confeccionó un programa en Matlab 2013 b. En la figura 4 se observa el crecimiento del flujo termosifónico al aumentar la radiación solar incidente y al aumentarla relación longitud/diámetro del tubo. La figura 5 muestra el crecimiento del flujo respecto a la radiación incidente y el ángulo de inclinación (respecto a la horizontal).Se observa que al aumentar el ángulo para pequeños valores de éste (< 20o), la variación del flujo es más notable que para ángulos mayores.
La variación del flujo termosifónico muestra una dependencia directa respecto a la relación longitud diámetro del tubo absorbedor y con la radiación incidente (absorbida) en el tubo colector. Esto corrobora el aumento de la energía útil al aumentar el área de captación para un coeficiente de pérdida determinado.
Los resultados de esta ecuación fueron comparados a los resultados de los trabajos de [1, 15 ] obteniéndose buena correspondencia para valores de relación de áreas ε = 0,5.
CONCLUSIONES
Se obtuvo una ecuación para la determinación del flujo termosifónico que se establece en un colector de tubos evacuados todo cristal (CTETC) sometido a la radiación solar. Esta ecuación fue obtenida bajo la consideración de no igualdad del área de flujo de la corriente caliente y fría que se establece en el tubo colector.
Además se logró el comportamiento del flujo en función del ángulo de inclinación y de la relación longitud/diámetro del tubo evacuado.
REFERENCIAS
1. Tang R, Yang Y, Gao W. Comparative studies on thermal performance of water-in-glass evacuated tube solar water heaters with different collector tilt-angles. Solar Energy. 2011;85:1381-9. ISSN 0038-092X.
2. Dabra V, Yadav L, Yadav A. The effect of tilt angle on the performance of evacuated tube solar air collector: experimental analysis. International Journal of Engineering, Science and Technology. 2013;5(4):100-10. ISSN 2141-2820. DOI http://dx.doi.org/10.4314/ijest.v5i4.9.
3. Al-Mashat SMS, Hasan AA. Evaluation of Convective Heat Transfer and Natural Circulation in an Evacuated Tube Solar Collector. Journal of Engineering. 2013;19(15). ISSN 2051-3305.
4. Yadav A, Bajpai VK. An Experimental Study on Evacuated Tube Solar Collector for Heating of Air in India. International Science Index World Academy of Science, Engineering and Technology. 2011;5(7):81-6. ISSN 2010-376X.
5. Li Z, et al. All-glass vacuum tube collector heat transfer model used in forced-circulation solar water heating system. Solar Energy. 2010;84:1413-21. ISSN 0038-092X.
6. Gao Y, et al. Effects of thermal mass and flow rate on forced-circulation solar hot-water system: Comparison of water-in-glass and U-pipe evacuated-tube solar collectors. Solar Energy. 2013;98:290-301. ISSN 0038-092X. DOI http://dx.doi.org/10.1016/j.solener.2013.10.014.
7. Pei G, et al. Comparative Experimental Analysis of the Thermal Performance of Evacuated Tube Solar Water Heater Systems With and Without a Mini-compound Parabolic Concentrating (CPC) Reflector(C < 1). Energies. 2012;5:911-24. ISSN 1996-1073. DOI 10.3390/en5040911.
8. Sato AI, Scalon VL, Padilha A. Numerical Analysis of a Modified Evacuated Tubes Solar Collector. In: International Conference on Renewable Energies and Power Quality; Santiago de Compostela (Spain); 2012.
9. Shahi M, Mahmoudi AH, Talebi F. Numerical simulation of steady natural convection heat transfer in a 3-dimensional single-ended tube subjected to a nanofluid. International Communications in Heat and Mass Transfer. 2010;37:1535-45. ISSN 0735-1933.
10. Zhu H. Theoretical and experimental study on single-phase natural circulation under inclined conditions. Journal of Nuclear Science and Technology. 2013;50(3):304-13. ISSN 0022-3131.
11. McEligot D, Denbow D, Murphy H. Transient natural convection in heated inclined tubes. Energy. 1990. ISSN 0360-5442.
12. Munson BR, et al. Fundamentals of fluid mechanics. Seventh ed. United States of America: John Wiley & Sons, Inc; 2013. p. 796. ISBN 978-1-118-11613-5.
13. Bergman TL, et al. Fundamental of heat and mass transfer. Seventh ed: John Wiley & Sons; 2011. p. 567. ISBN 978-0470-50197-9.
14. Duffie J, Beckman W. Solar Engineering of thermal processes. Fourth ed. USA: John Wiley & Sons, Inc; 2013. p. 928. ISBN 978-0-470-87366-3.
15. Idowu OS, Olarenwaju OM, Ifedayo OI. Determination of optimum tilt angles for solar collectors in low-latitude tropical region. International Journal of Energy and Environmental Engineering. 2013;4(29). ISSN 2251-6832.
Recibido: 12 de septiembre de 2015.
Aceptado: 2 de diciembre de 2015.
César Cisneros-Ramírez. Instituto Superior Politécnico José Antonio Echeverría, Facultad de Ingeniería Mecánica. La Habana, Cuba
Correo electrónico: cesar@ceter.cujae.edu.cu