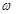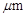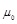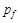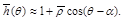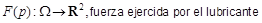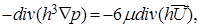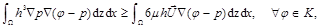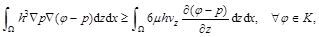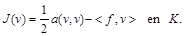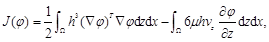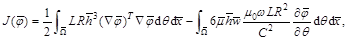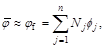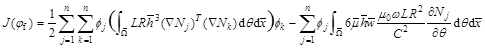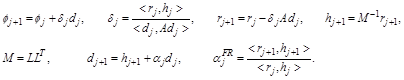Artículo Original

Algoritmo para determinar cavitación en un par eje-cojinete con ranura axial y desalineación paralela

An algorithm to determine cavitation in a journal bearing with axial groove and parallel misalignment

Hassán Lombera-Rodríguez¹  , Carlos Eulalio Novo-Soto¹ 

¹Universidad de las Ciencias Informáticas, La Habana, Cuba. Correo electrónico: [e-mail]

Resumen

El objetivo del trabajo fue proporcionar un algoritmo computacional para predecirla ocurrencia de la cavitaciónen el lubricante de un par eje-cojinete,sometido a un desplazamiento radial conocido.El dispositivo se compone de un cilindro exterior que rodea un eje, ambos separados por un lubricante que evita el contacto. Se considera una ranura de alimentación axial y una desalineación paralela. Las incógnitas del problema son el campo de presión del lubricante, que satisface el modelo de cavitación de Reynolds, y la fuerza ejercida por este. El problema se resuelve computacionalmente mediante un método de gradiente conjugado precondicionado, modificado con técnicas de proyección y reinicialización para afrontar la cavitación. La estrategia numérica adoptada explota las propiedades del modelo matemático subyacente y aporta otra forma de solución al problema en cuestión, diferente de las que existen en la literatura.

Palabras-clave: cavitación; desalineación paralela; gradiente conjugado precondicionado; par eje-cojinete

Abstract

The objective of this paper is to provide a computational algorithm to predictcavitation within the lubricant of a journal bearing subjected to parallel misalignment. The device consists of an external cylinder surrounding a rotating shaft, both separated by a lubricant to prevent contact. An axial supply groove is considered as well as a parallel misalignment. The unknowns of the problem are the lubricant pressure field, satisfying the Reynolds cavitation model, and the force exerted by this. The problem is solved by the preconditioned conjugate gradient method, modified with both projection and restarting strategies to account for cavitation. The numerical approach takes advantage of the underlying mathematical model and provides another way of solution to the related problem, different from the ones that exist in the literature.

Key words: cavitation; parallel misalignment; preconditioned conjugate gradient method; journal bearing

Introducción

Tradicionalmente, para comprobar un par eje-cojinete se ha tenido en cuenta sus propiedades físicas, su régimen de explotación, así como las aproximaciones para el campo de presión de Sommerfeld y Ocvirk, para cojinetes infinitamente largos y cortos respectivamente. Dichas aproximaciones realizan simplificaciones a la ecuación de Reynolds. La solución de Sommerfeld descarta el flujo axial en el dispositivo, mientras que la aproximación de Ocvirk asume que en pares eje-cojinetes cortos el flujo circunferencial es menos importante [¹, ²]. Ambas aproximaciones, definidas mediante expresiones analíticas, resultan apropiadas para relaciones geométricas específicas en un par eje-cojinete. Así, han sido utilizadas por los ingenieros a lo largo de los años. Sin embargo, no captan la realidad observada en la práctica, especialmente cuando se necesita predecir un fenómeno tan significativo como la cavitación. La cavitación es un efecto hidrodinámico que implica un cambio súbito de la fase líquida a vapor. Ocurre siempre que la presión local en el fluido es igual o menor que su presión de saturación.

En el caso de un par eje-cojinete, tiende a presentarse cerca de las ranuras de alimentación o en las superficies de los cojinetes orientadas en la dirección de aplicación de las mayores cargas. Finalmente, se traduce en enormes gastos por reparo o reposición de estos equipos y por tal motivo es un suceso indeseable. En Teoría de la Lubricación, la cavitación se define como la ruptura de la película continua de lubricante, debido a la formación de burbujas en el interior de este [³]. La presencia de dos regiones diferentes, la primera cubierta por una película continua de lubricante y la segunda por una película parcial, han sido observadas experimentalmente en muchos dispositivos lubricados. Dicha peculiaridad hace que el fenómeno no pueda ser modelado directamente mediante la clásica ecuación de Reynolds. Se impone así la utilización de modelos matemáticos que contemplen dicho fenómeno. En general, su estudio en pares eje-cojinetes ha sido una tendencia constante en la comunidad de Tribología [⁴, 8].

Los modelos matemáticos en Teoría de la Lubricación asumen que la presión incógnita p es constante a través del espesor de la película fluida (flujo laminar). Esto permite aproximar las ecuaciones tridimensionales de Navier-Stokes por la ecuación bidimensional de Reynolds. Una amplia revisión que concierne todo el análisis físico matemático de los diferentes modelos de cavitación existentes en la literatura fue realizado por Bayada y Vázquez en [³]. La característica común consiste en la descomposición del dominio en dos partes: una región lubricada donde se verifica la ecuación de Reynolds y una región cavitada donde la presión se toma como una constante (la presión de saturación). La diferencia entre estos modelos viene de las condiciones impuestas en la frontera libre que separa las regiones lubricadas y cavitadas. Los dos más ampliamente utilizados son los modelos de Reynolds (Swift-Stieber) y de Elrod-Adams [⁹].Varios artículos han utilizado la teoría de las inecuaciones variacionales aprovechando el hecho de que la presión en la región lubricada es mayor que la presión de saturación. La idea derivó en el modelo de cavitación de Reynolds [³]. Por su parte, en el modelo de Elrod-Adams se introduce la hipótesis de que en la zona de cavitación existe una mezcla de fluido y aire, definiendo una nueva variable que representa la concentración de lubricante [⁹].

Este modelo, que también descansa en la ecuación de Reynolds, ha sido ampliamente utilizado en Tribología. Dado su aparente realismo físico, varios esfuerzos se han dirigido a la realización de rigurosos análisis matemáticos (existencia, unicidad) y simulaciones numéricas con apropiadas y justificadas técnicas [⁵]. A diferencia de otros modelos, permite caracterizar el fenómeno de falta de alimentación. Su interés también radica en la evidencia de que es un modelo que preserva la masa. Vale destacar que los experimentos realizados con ambos modelos de cavitación han arrojado los mismos resultados en ausencia de rugosidad. En adición, el modelo de cavitación de Reynolds, debido a su naturaleza y fácil implementación computacional, ha sido utilizado en varios estudios matemáticos; véase por ejemplo los trabajos de Bayada y Vázquez en [³] y las referencias dentro de este. En el presente trabajo se utilizará igualmente dicho modelo. Vale destacar que, en la literatura, la resolución numérica de dicho modelo contempla técnicas basadas en el Método de Elementos Finitos (MEF).

El problema discreto ha sido resuelto mediante el método de Gauss-Seidel o mediante el método de sobre-relajación, incluyéndose en ambos casos técnicas de proyección para considerar la cavitación. Estas estrategias parecen ser suficientes, en el sentido de que resuelven el problema, pero en las aplicaciones ingenieriles reales, la discretización de la geometría se realiza con una malla muy fina, lo cual implica no solo matrices dispersas de grandes dimensiones sino también mal condicionadas. Bajo estas circunstancias, estas estrategias numéricas clásicas resultan muy lentas desde un punto de vista computacional, inaceptables si el modelo directo debiera anidarse dentro de un problema más complejo, e.g. en la resolución de un problema inverso. Por esta razón, resulta conveniente tomar ventaja del modelo matemático subyacente y elegir una estrategia numérica apropiada. Así, se propone en el presente trabajo la resolución del modelo de cavitación de Reynolds mediante la minimización de un funcional convexo, utilizando el algoritmo Gradiente Conjugado Precondicionado (GCP) con estrategias de proyección y reinicialización. En este sentido, esta propuesta constituye el principal resultado del presente trabajo, donde se considera además un cojinete con ranura de alimentación axial, en régimen estacionario y con un lubricante incompresible, isotérmico, e isoviscoso. Se asume que el eje del dispositivo puede desplazarse paralelamente al eje del casquillo.

Es preciso resaltar que, para los ingenieros, resulta interesante la predicción de la posición final del eje cuando se somete a una carga radial conocida, con la finalidad de predecir el contacto, así como la ocurrencia de la cavitación. Matemáticamente, la solución supone resolver un problema inverso reconocido en Teoría de la Lubricación, con algunos estudios realizados; véase por ejemplo los trabajos de [⁴, ⁵, ¹⁰]. Igualmente, se prevé la continuación del presente trabajo con la resolución numérica de dicho problema inverso. El objetivo del presente trabajo es proveer un algoritmo computacional para predecirla ocurrencia de la cavitación en el lubricante de un par eje-cojinete, sometido a un desplazamiento radial conocido.

Métodos y Materiales

Se propone un algoritmo computacional para predecir la ocurrencia de la cavitación en el lubricante de un par eje-cojinete,sometido a un desplazamiento radial conocido. La predicción se realiza modelando inicialmente la holgura radial y la cavitación en el lubricante. Luego, se determina el campo de presión en el dispositivo, que permitirá identificar la ocurrencia de zonas cavitadas para un desplazamiento concreto del eje.Las constantes geométricas y físicas del par eje-cojinete utilizado en las simulaciones computacionales de este trabajo fueron tomadas de análisis experimentales realizados por Pierre, Bouyer y Fillonen [¹¹], relacionadas en la tabla 1.

Tabla 1 Constantes geométricas y físicas utilizadas en las simulaciones 

Parámetro	Símbolo	Unidad	Valor
Velocidad angular del eje		rpm	1500
Longitud del par eje-cojinete	L	mm	80
Holgura radial	C		117,5
Radio del eje	R	mm	49,89
Viscosidad del fluido		Pa·s	0,023
Viscosidad de referencia		Pa·s	0,0813
Presión atmosférica		MPa	0,101325
Presión de alimentación		MPa	0,08
Posición angular		grados (º)	35
Excentricidad relativa		adimensional	0,6

La figura 1 presenta la sección transversal de un par eje-cojinete de ejemplo. A partir de esta se deduce una expresión para el espesor h de la película fluida existente entre el eje y el casquillo del dispositivo analizado.

Fig. 1 Sección transversal de un par eje-cojinete de ejemplo 

El modelo caracteriza la desalineación paralela, donde el eje del dispositivo puede desplazarse con dos grados de libertad. Definiendo C como la resta entre los radios respectivos Rb y R, el espesor queda definido como, ecuación 1:

(1)

Seala excentricidad relativa con valores entre 0 y 1. Vale destacar que la ecuación 1 es válida solo si C/Rb << 1. En lo sucesivo, se trabajará con la expresión adimensional para h definida como . Por otra parte, en la figura 1 se aprecia la relación 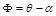, por lo que la ecuación 1 puede ser escrita, teniendo en cuenta lo anterior como:

(2)

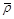donde y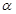 especifican la posición del eje en coordenadas polares. Esta última expresión será la utilizada para definir el espesor h en la presente investigación. Resulta necesario notar además en la ecuación 2 la expresión resultante para el mínimo valor de 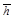, cuando el , por tanto, ecuación 3:

(3)

Modelización matemática de la cavitación

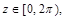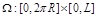Sea L y R la longitud y el radio de la sección transversal del eje respectivamente. Se considera la coordenada circunferencial desdoblada así como la coordenada axial Se define la región . Las incógnitas del problema, para 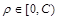y conocidos son:

Bajo determinadas condiciones de operación en un par eje-cojinete, la presión del lubricante puede alcanzar cierto valor mínimo, relacionado con su presión de saturación, por debajo de la cual ocurre el fenómeno de la cavitación. La región cavitada se ocupa así por vapor a una presión constante .

Se tomará un valor de 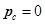como una aproximación de la presión a la cual ocurre dicho fenómeno. En estas condiciones la conocida ecuación de Reynolds para fluidos incompresibles e isoviscosos en régimen estacionario (ecuación 4),

(4)

pierde validez, por lo que resulta necesaria otra formulación que contemple dicho fenómeno. Se necesita así, buscar una función p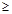0 en la región que describe el cojinete, tal que se cumpla la ecuación de Reynolds donde p>0. Dado que no ocurre intercambio alguno de masa a través de la frontera de la región estudiada es posible afirmar que , con la normal a dicho contorno. Así, es posible utilizar una de las variantes existentes en la literatura para modelar este fenómeno basado en la inecuación variacional de Reynolds (5), cuya formulación débil fue obtenida a partir de la ecuación 4. La demostración es sencilla, basta con multiplicar por una función test e integrar en ambos miembros con el teorema de la divergencia.

(5)

Con

(6)

Donde 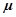significa la viscosidad del fluido y el vector hace referencia al vector velocidad del eje. En el problema abordado, el eje solo presenta una única componente de velocidad no nula, 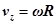, con 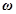la velocidad angular. Vale destacar que el modelo en la ecuación 5 es conocido en la literatura como modelo de Reynolds para la cavitación o de Swift-Stieber.

Modelo analítico para el cálculo de la presión

Tras efectuar la multiplicación 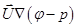en la ecuación 5 se tiene la siguiente simplificación:

(7)

definido en la ecuación (6). A continuación, se define la aplicación bilineal a y la función f como:

y se reescribe la expresión 7 como sigue:

cuya solución es equivalente a encontrar el mínimo del funcional descrito en la ecuación 8:

(8)

Tomando los parámetros de la ecuación 7 e insertándolos en la expresión 8 se obtiene el funcional a minimizar:

(9)

con h definida en la ecuación 1. Para hacer la solución adecuada para una amplia variedad de problemas se introducen las siguientes variables adimensionales:

Donde representa la viscosidad de referencia. Así, se transforma el dominio del problema en el dominio adimensional 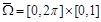, para las coordenadas . Luego, la ecuación adimensional para el funcional en la expresión 9 será:

(10)

con h definida en la ecuación 2.

Cálculo de la fuerza ejercida por el lubricante

La presión p es una magnitud física que mide la proyección de la fuerza, en una dirección perpendicular a la superficie, por unidad de área. Así, las componentes radiales de la fuerza dimensional ejercida por el lubricante sobre el cojinete serán:

donde y 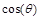representan las componentes del vector normal unitario a la superficie del cojinete. De acuerdo a los cambios de variables realizados en la ecuación 10 se obtienen las siguientes expresiones adimensionales para las componentes radiales de la fuerza ejercida por el lubricante:

(11)

Discretización del modelo matemático

Aprovechando las características de la región en estudio se realiza una discretización espacial mediante elementos finitos cuadriláteros, lineales a trozos. Esto es, la incógnita 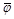se aproxima como:

(12)

donde el subíndice “f” alude a la aproximación hecha mediante el MEF. Las 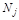son las conocidas funciones de forma, descritas fácilmente mediante los polinomios de Lagrange y los los valores de la incógnita en los nodos de la discretización. Así, la forma discretizada del funcional 10 será:

(13)

Puede notarse fácilmente que el funcional es de la forma .

Algoritmo numérico

Para la resolución del problema planteado se propone un algoritmo tipo GCP, ideal para funcionales cuadráticos con matrices definidas positivas, como el que se resuelve en el presente trabajo. Sin embargo, con la estrategia regular del algoritmo, para configuraciones que provoquen cavitación se obtienen soluciones fuera del conjunto convexo definido en la ecuación 6. Dichas soluciones, con valores de presión negativos carecen de significado físico. Se necesita así garantizar que la presión nunca sea negativa. En este trabajo se adapta el algoritmo GCP, con una técnica de proyección para afrontar la cavitación. Se ejecuta un proceso de reinicialización cuando ésta ocurre. La estrategia corrige las componentes de presión negativas, así como las componentes respectivas del gradiente cuando se detectan soluciones fuera del convexo. Se utiliza la técnica de proyección max(, 0).

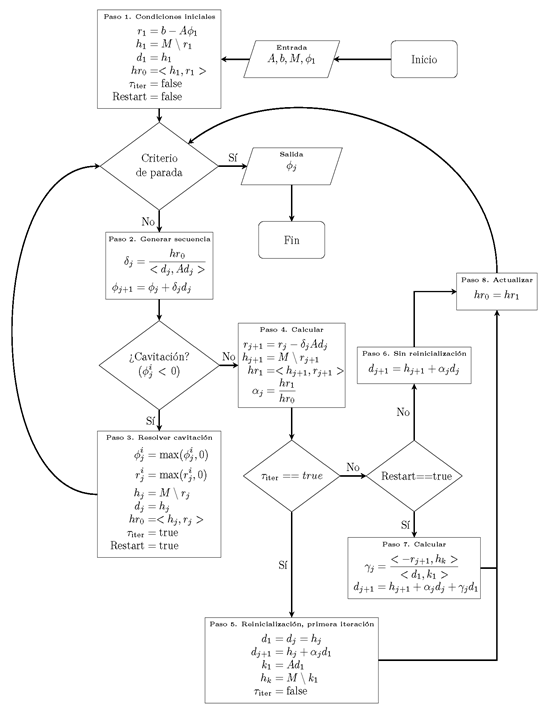
En la figura 2 se muestra el diagrama de flujo para el algoritmo propuesto tipo GCP, modificado con la técnica de proyección y de reinicialización. En consecuencia, se calculan apropiadamente las expresiones para las nuevas direcciones de descenso del algoritmo, cuando se considera la técnica de precondicionamiento. En este sentido el trabajo propone una alternativa nueva para la resolución del mapa de presiones en un par eje-cojinete considerando el fenómeno de la cavitación. En resumen, en la iteración clásica, en ausencia de cavitación y reinicialización (Pasos 2,4,6,8), se utilizan las expresiones en (14), clásicas del algoritmo GCP.

(14)

Esto es, iniciando con una solución elegida 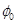se genera una secuencia de iteraciones donde significa la dirección de desplazamiento y la longitud del paso. El vector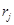 representa el resto, A la matriz del sistema y el parámetro caracteriza una implementación concreta del método, Fletcher-Reeves en este trabajo. La notación <, > representa el producto escalar. La matriz M es el precondicionador del sistema. Cuando se detecta la cavitación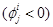, las componentes negativas de la presión y el gradiente se establecen en cero. Se aplica en este paso la técnica de proyección. Luego, se calcula el término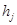, pero utilizando el valor del residuo actualizado 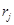.El proceso de reinicialización se prepara estableciendo 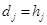, calculando el producto 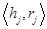y definiendo dos banderas (Paso 3). Así, en la primera iteración de la reinicialización se establecen y se calculan (cuando 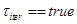)las expresiones siguientes (Paso 5):

Las iteraciones subsiguientes (cuando Restart == true) consideran el cálculo de las direcciones de búsqueda como se propone en este trabajo (Paso 7). En particular se modifica el cálculo del término 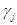de la técnica de reinicialización clásica, con la solución de un sistema de ecuaciones (calculado una vez por reinicialización) que garantiza seguir disfrutando de las bondades del precondicionamiento.

Fig. 2 Diagrama de flujo para el algoritmo computacional propuesto 

Resultados y Discusión

En esta sección se presentan los resultados numéricos que permiten verificar al acople de las distintas estrategias numéricas empleadas. Para ello, el dominio adimensional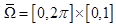 se discretiza utilizando una malla de elementos finitos de 400 x 160 (64000 elementos cuadriláteros). Aunque el problema se resuelve en un domino adimensional, la mayoría de los resultados son transformados y presentados en sus escalas y unidades reales.

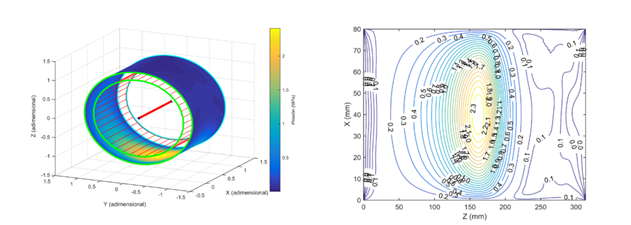
La figura 3, a la izquierda, muestra la obtención del mapa de presiones luego de aplicar el algoritmo propuesto en el par eje-cojinete de estudio. Se observa la zona cavitada, en la región divergente y alrededor de la ranura de alimentación axial (zona superior), tal y como se recoge en el artículo de Bayada y Vázquez [³]. Vale destacar que la cavitación aparece ligeramente desplazada debido a la rotación del eje. A la derecha, se presentan las isolíneas de presión para el experimento realizado. Ambos gráficos verifican el pico de presión obtenido, así como la localización de la región cavitada.

Fig. 3 Mapa de presiones en el par eje-cojinete a la izquierda e isolíneas de presión a la derecha 

La figura 4 muestra a la izquierda el perfil de la holgura radial para la simulación realizada. El valor mínimo calculado de la holgura fue de 47, localizado en la coordenada angular y excentricidad referidas en la tabla 1. A la derecha se muestrael comportamiento de la fuerza ejercida por la presión cuando la excentricidad aumenta. El experimento verifica que, para el caso con desalineación paralela, donde el caso límite sería el contacto en una línea, la capacidad de carga del par eje-cojinete tiende a infinito [¹²]. Este resultado es teórico y en la práctica no sucede así debido a otros factores subyacentes en el funcionamiento real de dichos dispositivos, tales como la desalineación angular. En el experimento, la excentricidad relativa varía en el intervalo de 0,1 a 0,7 para propósitos de reproducción.

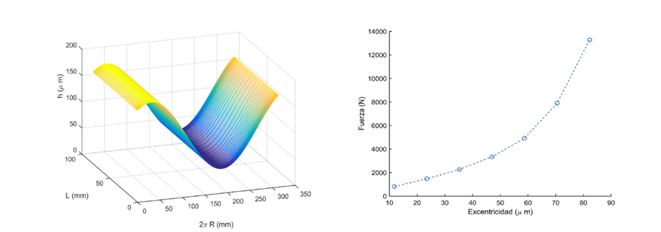
Fig. 4 Perfil de la holgura radial (izquierda) y comportamiento de la fuerza ejercida por el lubricante cuando la excentricidad aumenta (derecha) 

La estrategia abordada provee a los ingenieros un algoritmo que, bajo las consideraciones del presente trabajo, predice la cavitación en un par eje-cojinete con desalineación paralela. El efecto destructivo de la cavitación ha justificado el desarrollo de modelos numéricos que permitan predecir las características de operación de los pares eje-cojinetes en estado estacionario [¹¹]. El modelo numérico propuesto, si bien no contempla todos los fenómenos subyacentes en el funcionamiento de un par eje-cojinete, ayudaría en una primera instancia a predecir, para una excentricidad conocida, estos daños en los dispositivos. Dichas afectaciones traen consigo serias implicaciones económicas. La cavitación, puede provocar conjuntamente con el contacto metal-metal desgaste adhesivo, abrasivo y erosión. Sin dudas son daños serios para la Industria, pues conllevan a la parada de una maquinaria productiva en funcionamiento, a un proceso de desensamble para sustituir las partes afectadas con la correspondiente pérdida de tiempo y recursos económicos.

Conclusiones

Es posible predecir la cavitación en el lubricante de un par eje-cojinete sometido a un desplazamiento radial conocido, mediante la minimización apropiada de un funcional. Para ello debe modelarse el problema mediante la inecuación variacional de Reynolds, transformarse a un funcional convexo y utilizarse el algoritmo gradiente conjugado precondicionado descrito, con técnicas de proyección y reinicialización. En este contexto se provee una estrategia numérica de solución diferente a las recogidas en la literatura, en la que se explotan las propiedades del modelo matemático subyacente.

Referencias

1.  Ocvirk FW, Dubois GB. Analytical derivation and experimental evaluation of short-bearing approximation for full journal bearings. NACA.1157. USA; 1953.

2.  Sommerfeld A. Zur hydrodynamischen theorie der schmiermittelreibung. Z. Math. Phys.1904;50:97-155.

3.  Bayada G, Vázquez C. A survey on mathematical aspects of lubrication problems. Boletín SeMA. 2007;39:37-74.

4.  Ciuperca IS, Jai M, Tello JI. Equilibrium analysis for a mass-conserving model in presence of cavitation. Nonlinear Analysis: Real World Applications. 2017;35:250-264.

5.  Lombera H, Tello JI. A numerical approach to solve an inverse problem in lubrication theory. Rev R Acad A. 2014;108(2):617-631.

6.  Jang JY, Khonsari MM. On the Characteristics of Misaligned Journal Bearings. Lubricants. 2015;3(1):27-53.

7.  Xu G, Zhou J, Geng H, et al. Research on the static and dynamic characteristics of misaligned journal bearing considering the turbulent and thermohydrodynamic effects. Journal of Tribology. 2015;137(2): 25-34.

8.  Sun J, Zhu X, Zhang L., et al. Effect of surface roughness, viscosity-pressure relationship and elastic deformation on lubrication performance of misaligned journal bearings. Industrial Lubrication and Tribology. 2014;66(3):337-345.

9.  Elrod HG, Adams ML. A computer program for cavitation and starvation problems. In: Cavitation and related phenomena in lubrication: proceedings of the 1st Leeds-Lyon Symposium on Tribology,Leeds, England: Mechanical Engineering Publications;1975.

10.  Dager R, Negreanu M, Tello JI. An inverse problem for the compressible Reynolds equation. Q. Appl. Math. 2015;73(4):607-614.

11.  Pierre I, De France E, Bouyer J, et al. Thermohydrodynamic Behavior of Misaligned Plain Journal Bearings: Theoretical and Experimental Approaches. Tribology Transactions. 2004;47(4):594-604.

12.  Ciuperca IS, Jai M, Tello JI. On the existence of solutions of equilibria in lubricated journal bearings. SIAM J Math Anal. 2009;40(6):2316-2327.

Recibido: 15 de Octubre de 2017; Aprobado: 04 de Diciembre de 2017