Introducción
En el ámbito educativo que encierra experiencias de aprendizaje, se ha visto con frecuencia el uso de metodologías de la enseñanza de la matemática, centradas en darle al niño una definición o una fórmula, en la resolución de problemas apegada a patrones de imitación, ocasionando algunas veces la limitación en el uso de nuevas estrategias que promuevan el desarrollo de procesos matemáticos. El planteamiento de la construcción de pensamientos matemáticos está ligado al desarrollo cognoscitivo, por cuanto, la niña y el niño conoce, aprende y piensa, lo que permite inferir que se está en presencia de un enfoque interaccionista del aprendizaje. Este se diferencia del conductista cuando se plantea, que no solo se aprende de experiencias externas, o solo a partir de la razón, como lo indican los racionalistas, sino que el conocimiento surge de una indisociable interacción entre la experiencia real y la razón.
En consecuencia, las etapas de desarrollo cognitivo propuestas por Piaget (1979) se ven afectadas por dos situaciones que determinan el accionar del niño en situaciones de aprendizaje: la primera tiene que ver con la interacción entre el niño y el objeto, donde la interpretación de la realidad es producto de su esquema mental ya estructurado; y la segunda tiene que ver con acciones donde los objetos y situaciones influyen sobre los esquemas del niño, modificándolos.
En función de lo anterior, de la teoría cognitiva de Jean Piaget, se desprende el área de aprendizaje lógico-social, y es allí donde se hace referencia al componente de procesos matemáticos con énfasis al reconocimiento y uso del número, y también a las relaciones que se establecen entre los objetos y al conocimiento lógico matemático (clasificación, seriación y número), al conocimiento espacio temporal, y la representación.
Es por ello que, desde la didáctica, se logra la integración de los nuevos conocimientos con los ya existentes, siendo un proceso muy complejo que requiere de múltiples y variadas situaciones de aprendizaje, tiempo y oportunidades, para que las niñas y niños pongan en juego ciertas acciones, comparar, establecer relaciones, transformar, analizar, entender los resultados, el proceso a seguir, ensayar una posible solución, y justificar los resultados. Porque se hace necesario proponer, a las niñas y niños, situaciones didácticas contextualizadas en lo social, como punto de partida para planificar nuevos problemas a plantear.
En este sentido, el descubrimiento, la exploración, la práctica continuada, los procedimientos y la mediación intencionada del adulto, permitirán a las niñas y niños, apropiarse de los aprendizajes matemáticos. Por ello se incluye, en los currículos, los procesos matemáticos que debe abordar la o el educador: espacios y formas geométricas, la media y sus magnitudes, la serie numérica, el peso, la capacidad, el tiempo, y la longitud. Por consiguiente, el propósito de la indagación emerge del análisis de las características esenciales de las categorías apriorísticas del Desarrollo del Pensamiento Matemático y Estrategias Didácticas, cuya finalidad se centra en identificar e interpretar las estrategias didácticas que emplean las educadoras de párvulos para desarrollar el pensamiento matemático en niñas y niños entre 2 y 4 años de edad, dentro de las salas de clases.
La investigación se realizó bajo un enfoque cualitativo, apoyada en el paradigma pospositivista, y el método abordado fue fenomenológico. Distintas regiones de Chile sirvieron como contexto del estudio. Se realizó un muestreo basado en criterios para la selección de los informantes clave, y en total se seleccionaron 7 educadoras de párvulos, quienes hacen vida profesional en distintas instituciones educativas del país. La técnica para recabar información con respecto al fenómeno de estudio fue la entrevista en profundidad, y sus resultados se analizaron para la identificación de unidades de análisis, y, a su vez, para la generación de temas, subtemas y patrones que describan las experiencias y las conexiones narrativas de los participantes en relación con Desarrollo del Pensamiento Matemático y Estrategias Didácticas.
Enfoque Psicogenético desde la Reflexión de Jean Piaget
La profundidad del enfoque psicogenético va más allá de simples procesos, tales como percibir, recordar, evaluar e interactuar con otras personas (desarrollo cognitivo). Todos estos procesos son funciones que el cerebro y la mente pueden realizar de un modo rutinario. En este sentido para Piaget (1979), en el enfoque psicogenético predominan dos concepciones: la perspectiva natural de Piaget, y el procesamiento de la información. Desde la concepción de cognición, el sistema cognitivo es un sistema ampliamente activo, pues es capaz de asimilar la información activamente y seleccionar lo que le interesa adaptar para construir su propio conocimiento (asimilación). Es decir, que la mente siempre se encuentra reconstruyendo e interpretando la información que le llega del medio para ubicarlo en la mente del individuo dentro de su marco de referencia; en cierto sentido, este enfoque es más "realista", ya que, desde su visión, el sistema cognitivo es más adaptativo para el organismo (acomodación).
El enfoque psicogenético, de acuerdo con Piaget (1979), constituye el pilar esencial para el conocimiento humano, puesto que este se fundamenta en el vínculo existente entre medio ambiente y aprendizaje. Por su parte, la literatura especializada explica que, bajo este enfoque se establecen relaciones entre la mente (la psique humana) y la génesis (o genética para algunos); de esta manera el principal objetivo de estudio estuvo centrado de manera muy especial, a los procesamientos de la mente (pensamiento).
Aunque algunos teóricos difieren en determinados aspectos con las propuestas epistemológicas de Piaget, generalmente existen puntos de contacto. Por ejemplo, Vygotsky (1979) siempre estuvo atento a los postulados del enfoque genético de Piaget como aporte principal a su enfoque sociocultural. A este respecto, Raynaudo y Peralta (2017) resaltan lo siguiente:
… Vygotsky elogia y critica varios aspectos de la obra de Piaget. Se refiere a la obra de Piaget como una de las teorías del desarrollo del lenguaje y del pensamiento más completas. Ubica las fortalezas en la obtención de nuevos datos empíricos, la cultura científica del hecho psicológico, su análisis detallado, la clasificación de los materiales, el nuevo método clínico (p. 32).
De lo anterior se puede decir que, el desarrollo del pensamiento está basado en la búsqueda de mecanismos que inciden en los procesos de la mente, y, como ya se ha mencionado, Piaget (1976) sustenta las bases de su enfoque científico en los mecanismos de asimilación y acomodación. Por su parte, Vygotsky (1979) centra su idea en la internalización de la cultura. Sin embargo, esta noción de internalización es concebida por él basándose en una idea recuperada de Piaget, es decir, que, a pesar de contraponerse a algunos puntos señalados por este último, defiende que "la personalidad del niño se desarrolla al internalizar las actitudes de otros significativos hacia él" (Álvarez y Balmaceda, 2020, p. 8).
Sobre estas bases, el enfoque psicogenético construye sus postulados, en los procesos psicológicos superiores, vale decir, el plano interno o natural del individuo (el origen o la génesis) y su relación con la internalización (aunque él mismo Piaget no acuñara el término) de los procesos sociales que el mismo individuo vincula mediante los mecanismos antes mencionados.
En atención a esto, Arias (2017), basado en los planteamientos de Piaget, explica que en el desarrollo cognoscitivo del individuo sus experiencias previas median el enfrentamiento del sujeto a nuevos conocimientos, por lo que el mismo autor destaca que:
El impacto de la psicología genética sobre el área educativa ha sido importante, pese a que no fue la idea inicial de Piaget al formular la teoría aportar en este campo, sin embargo, sus aportes han sido altamente considerados en el ámbito educativo (p. 836).
Finalmente, debe señalarse que, para Piaget, el cerebro y la mente (pensamiento), actúan una vez que el individuo se enfrenta al medio: estas acciones, como bien lo describe este modelo de aprendizaje, contribuyen en la organización de información de los esquemas mentales, que luego van a hacer representados por el individuo en el medio social donde se desenvuelva.
Desarrollo del Pensamiento Matemático en Niñas y Niños de la Primera Infancia
El estudio de los procesos lógico-matemáticos en la niña y el niño ha sido, desde hace más de tres décadas, uno de los tópicos más investigados en el desarrollo cognoscitivo de la niñez. Jean Piaget es el precursor del desarrollo del pensamiento lógico matemático. Este desarrollo es considerado como base fundamental para la construcción de operaciones matemáticas en el individuo. No obstante, estos procesos no deben encuadrarse solamente a las nociones matemáticas, pues su comprensión va más allá de la mera formulación de operaciones. En este sentido, desarrollar en el niño los procesos lógico-matemáticos ayudarán a que este reconozca y comprenda su propio yo, el yo con el mundo que lo rodea, y cómo relacionarse con él.
Para una educadora o educador de párvulos, es vital reconocer la importancia de desarrollar en la niña y el niño procesos simples y lógicos que le permitirán desenvolverse dentro de los diferentes contextos sociales. El más importante de estos es el educativo, pues es allí donde creará círculos que sentarán sus bases sociales para un futuro exitoso. Es por ello que Piaget enfatiza la idea de fortalecer dichos procesos mediante la interacción del niño con el mundo, donde el docente debe ubicar estrategias adecuadas a la etapa evolutiva propuesta en su teoría, y que hasta el día de hoy ha sido el aporte más importante para el educador del nivel inicial.
En ese orden de ideas, Nieves et al. (2019) plantean que:
Uno de los principales objetivos de la enseñanza de la Matemática es desarrollar en los estudiantes un pensamiento lógico, flexible y creativo. El pensamiento racional es objeto de estudio de la Psicología y de la Lógica, este se manifiesta como proceso psíquico cognoscitivo y como resultado (p. 3).
Lo anterior reitera la importancia del desarrollo lógico-matemático, que Herlina (2015), citado por Nieves (2019) caracteriza como "el proceso cognitivo que comprende la representación, abstracción, la creatividad y la demostración matemática" (p. 2). Por esta razón, el objetivo principal a lograr por el educador del nivel inicial, sería encontrar formas adecuadas de didáctica en la enseñanza de contenidos a través del juego (la lúdica es el mejor amigo de la educadora) utilizando con ello, analogías simples, ilustraciones, modelaje, ejemplos, explicaciones, y demostraciones.
En atención a la didáctica, Lugo et al. (2019) destacan lo siguiente:
… en los contextos escolares recae un compromiso indelegable para propiciar los escenarios cargados de estrategias para desarrollar el pensamiento lógico-matemático, exigiendo de esta manera docentes capacitados en el dominio de nociones básicas que le permitan diseñar las estrategias pertinentes para potenciar estos aprendizajes (p. 3).
Dichas estrategias deben ir acompañadas o sustentadas por las Bases Curriculares de la Educación Parvularia (BCEP, 2018), ya que toda acción docente debe estar respaldada por la teoría fundamentada en función de los aprendizajes del niño. Tomando este punto de referencia, se destaca que las BCEP plantean que en la evolución del aprendizaje en el niño es vital que él construya sus propios conocimientos por medio de su interacción con el mundo social, donde va consolidando códigos lingüísticos, así como matemáticos, científicos y sociales.
En síntesis, las implicaciones didácticas en el desarrollo de procesos lógico-matemáticos en el niño se ven reflejadas en la planificación de las actividades, donde el docente debe manejar un amplio conocimiento y experticia sobre la etapa del desarrollo evolutivo del niño (Piaget 1991). Si el docente evidencia debilidades en tal situación, representaría para la práctica pedagógica la imposibilidad del logro de objetivos, que no es otro que el niño desarrolle un pensamiento lógico- matemático que le servirá de apoyo en las demás áreas de aprendizaje.
Cabe destacar que la investigación se centró en identificar e interpretar las estrategias didácticas que emplean las educadoras de párvulos para desarrollar el pensamiento matemático en niñas y niños entre 2 y 4 años de edad, dentro de las salas de clases.
Materiales y métodos
La investigación se enmarcó en el paradigma pospositivista con enfoque cualitativo, ya que desde la fenomenología empírica se pretendió comprender las experiencias comunes relacionadas con el Desarrollo del Pensamiento Matemático y Estrategias Didácticas de actores del proceso educativo en las distintas regiones educativas chilenas, con énfasis en algunas comunas. La comprensión de este fenómeno intenta generar una aproximación teórica que relacione las descripciones del pensamiento matemático y las unidades de análisis que emergieron de la comprensión a fin de transmitir la esencia de tal experiencia.
Es importante el reconocimiento en las investigaciones cualitativas, su carácter comprensivo e interpretativo, pero también lo es la validez. En tanto que se respeten las voces de los participantes durante el proceso de investigación y se alcance el objetivo propuesto, en esa medida un estudio de tipo cualitativo es válido. La representación de las expresiones de los actores intervinientes en el proceso de investigación debe ser producto de las realidades mentales en torno a un fenómeno definido que conduzcan a constructos individuales y colectivos. Lincoln y Guba (1985) consideran que la realidad, "es un conjunto de construcciones mentales de los seres humanos" (p. 5).
Planos de reducción fenomenológica
Desde la perspectiva fenomenológica, el procedimiento para recolectar la información se traduce en una serie de pasos que se inician con la definición del fenómeno de estudio, el compendio de las experiencias de los participantes, el análisis de las diversas narrativas de los participantes, la identificación de unidades de sentido, hasta llegar a la aproximación teórica en torno al fenómeno. La estrategia para la interpretación de los hallazgos, específicamente para el método fenomenológico, se encontró constituida por la reducción.
Inicialmente, se realizó la primera reducción fenomenológica que colocó a las investigadoras a reflexionar sobre los prejuicios, juicios o cualquiera referencia subjetiva en la selección de los informantes claves.
Luego, fue preciso ejercer las siguientes actividades y acciones:
construcción del guion de entrevistas;
abordaje del contexto geográfico para la interacción con los informantes claves (aplicación de la segunda reducción fenomenológica);
se realizó la planificación de aplicación en consenso de las entrevistas;
aplicación de las entrevistas, donde se utilizó la grabación como instrumento de recopilación de la información. En ella se obtuvieron registros de las experiencias comunes desde las voces de los actores;
se integraron temas específicos de acuerdo a los informantes claves;
se aplicó la técnica de la observación fenomenológica, despojándose de prejuicios para registrar la realidad con una profunda concentración y atención a todo lo dado en el momento de la entrevista, denotándose así, la segunda reducción fenomenológica;
se logró comprender y reflexionar sobre el significado de los fundamentos epistémicos, axiológicos y ontológicos que sustentan el Desarrollo del Pensamiento Matemático y Estrategias Didácticas; y
se decidió asumir como herramienta tecnológica para el análisis el uso del ATLAS.ti 7, tal procedimiento implicó que emergieran las categorías necesarias para la construcción de una aproximación teórica.
El último paso consistió en la elaboración de las descripciones protocolares, por medio de la transcripción fidedigna de cada entrevista en profundidad, tal como se presentó en su contexto natural. Se resalta que, en estas transcripciones protocolares, el material de análisis refleja el punto de vista de cada entrevistada, a partir de las experiencias vividas, por cuanto se transcriben las vivencias expresadas por las informantes.
El cumplimiento del proceso de categorización se abordó a partir de los pasos que se describen a continuación:
Desarrollo de la lectura general sobre las descripciones surgidas en cada protocolo, con el propósito de tener una visión amplia de las intenciones escritas de cada una de las informantes claves con relación a los presupuestos planteados.
Definición de las unidades emergentes. Se consideró, igualmente, una nueva lectura de las descripciones protocolares.
Denominación de los temas centrales, a partir de la selección, de forma lógica en relación con las expresiones manejadas por las informantes claves. Aquí se produce una agrupación por similitud para llegar a los temas esenciales para la construcción de las categorías fenomenológicas individuales sintetizadas (reducción fenomenológica).
Agrupación de expresiones reflejadas del tema central con ayuda de la herramienta tecnológica del ATLAS.ti 7 para proceder a la construcción de los temas esenciales y categorías fenomenológicas individuales sintetizadas.
Integración de estructuras particulares y generales sintetizadas, y con temas centrales propios a cada categoría y subcategoría, con la ayuda del ATLAS.ti 7.
Integración de todas las estructuras particulares a una estructura general que conduce definitivamente a la construcción de una aproximación teórica sobre el Desarrollo del Pensamiento Matemático y Estrategias Didácticas.
Resultados
Para la contextualización de los hallazgos es importante la descripción de las regiones que constituyeron el escenario ontológico de la indagación, y de esta manera se contó con elementos para la comprensión de las percepciones de los 7 informantes claves seleccionados. Seguidamente, se presenta la mencionada descripción
Región de Tarapacá: en esta región se observó que la mayoría de las educadoras tienen un promedio de 4 a 6 años laborando, trabajando la mayoría de ellas para la Junta Nacional de Jardines Infantiles (JUNJI), escuelas municipales y jardines infantiles con la modalidad Vía de Transferencia de Fondos (VTF). Su última capacitación ocurrió entre 2 y 4 años atrás, dictada por JUNJI.
Región de Arica y Parinacota: en la comuna de Arica, se ubica un grupo de educadoras de párvulos, las que tienen entre 7 y 9 años de servicio laborando para JUNJI, VTF, y Servicios Locales de Educación Pública (Servicios locales), su última capacitación fue hace más de 4 años, dictada por la Pontificia Universidad Católica de Chile (PUC), y aplican estrategias en base a juegos y el enfoque Reggio Emilia. En esta región se consigue otro grupo de educadoras, con más de 18 años de servicios, laborando en colegios particulares subvencionado y en servicios locales; su última capacitación sucedió entre 2 y 4 años antes, recibida del Ministerio de Educación (Mineduc).
En la Región de Valparaíso, la cual incluye las comunas de La Serena, San Antonio, Villa Alemana y Cartagena, el promedio de años de servicio oscila entre los 10 y 12 años, laborando la mayoría de ellas para colegios particulares subvencionados, JUNJI, y escuelas municipales, habiendo recibido la última capacitación hace un año, de parte de la Pontificia Universidad Católica, y JUNJI.
En la Región de 0'Higging, integrada por las comunas de Villa del Mar, Placilla y Rancagua, las educadoras de párvulos, con tiempo de servicio entre los 10 y 15 años, trabajan en colegios particulares subvencionados, escuelas municipales, Fundación INTEGRA (INTEGRA), y VTF, siendo su última capacitación hace más de 4 años.
En la Región del Maule, las educadoras de las comunas de Villa Alegre y Chanco poseen entre 16 y 18 años de servicio en colegios particulares subvencionados e INTEGRA, con más de cuatro años desde la última capacitación entregada por INTEGRA.
En la Región del Bío Bío, las educadoras se desempeñan en las comunas de Santa Bárbara y Talcahuano. Ellas tienen en promedio 15 años laborando para INTEGRA, y VTF, recibiendo su última capacitación hace 4 años por parte de INTEGRA.
En la Región del Ñuble: la educadora entrevistada ha laborado más de 18 años en un colegio particular subvencionado, y su última capacitación fue entre 2 y 4 años atrás.
La Región Metropolitana comprende las comunas de Recoleta, Peñalolén, Lampa, Maipú, San Bernardo, Lo Prado, Ñuñoa, Huechuraba, Puente Alto, y La Florida, entre otras. Acá, se observó que, en las comunas de Recoleta, Peñalolén y Huechuraba, las educadoras tienen en promedio 18 años laborando, en establecimientos con dependencia municipal, habiendo recibido la última capacitación entre 2 y 4 años antes, impartida por el Departamento de Administración de Educación Municipal (DAEM). En las comunas de Lampa, Maipú, y San Bernardo, las educadoras tienen en promedio 7 y 9 años laborando, siendo de dependencia municipal, y VTF; con más de 4 años sin recibir capacitación.
En las comunas de Lo Prado y Ñuñoa, el promedio de tiempo de servicio se ubica entre 13 y 15 años, siendo de dependencia VTF, Particulares Subvencionados, y JUNJI, teniendo hasta 4 años sin recibir capacitación.
En las comunas de Puente Alto y La Florida, las educadoras tienen entre 4 y 6 años de ejercicio, pertenecen al sector Particular Subvencionado, y VTF. Su última capacitación fue entre 2 y 4 años antes, recibida a través de JUNJI, y del Centro de Perfeccionamiento, Experimentación e Investigaciones Pedagógica (CPEIP).
En las comunas de Puente Alto y La Florida, las educadoras tienen entre 2 y 4 años de experiencia, siendo de dependencia Particular Subvencionada, y VTF; aproximadamente las educadoras tienen 4 años sin recibir capacitaciones.
En la Región de La Araucanía, con las comunas de Temuco, y Victoria, las educadoras han estado laborando es entre 7 y 9 años, en lugares dependientes de INTEGRA y en colegios particulares subvencionados. Tienen un año desde su última capacitación, brindada por la Universidad Diego Portales, INTEGRA, y la Fundación Seminarium.
En las comunas de Ancud, Osorno, Llanquihue y Puerto Montt, ubicadas en la Región de Los Lagos, se encuentra que en Ancud y en Osorno el promedio de tiempo de servicio de las educadoras sobrepasa los 18 años, en establecimientos con dependencia municipal, JUNJI, y colegio particular subvencionado, con capacitaciones recibidas entre 2 y 4 años antes, las que fueron dictadas por la Agencia para la Educación Francesa en el Extranjero (AEFE), y la PUC. En la comuna de Llanquihue, las educadoras tienen en promedio 18 años de labor, dependientes de colegios particulares subvencionados, con capacitación dada hace 4 años, por parte de Mineduc. En la comuna de Puerto Montt, hay educadoras con experiencia laboral de 2 a 3 años, y hasta de 18 años de servicios, pertenecientes a INTEGRA y escuelas municipales, con su más reciente capacitación ocurrida hace 4 años, a cargo de CPEIP.
En la Región de Aysén, en las comunas de Cisnes y de Aysén, las educadoras tienen experiencias laborales que van desde los 12 a los18 años, de dependencia municipal y VTF, teniendo más de 1 año sin capacitación.
Por último, en la Región de Magallanes, en la comuna de Punta Arenas, la educadora posee experiencia entre los 12 a 18 años, labora en un colegio particular subvencionado, y su última capacitación tuvo lugar hace un año.
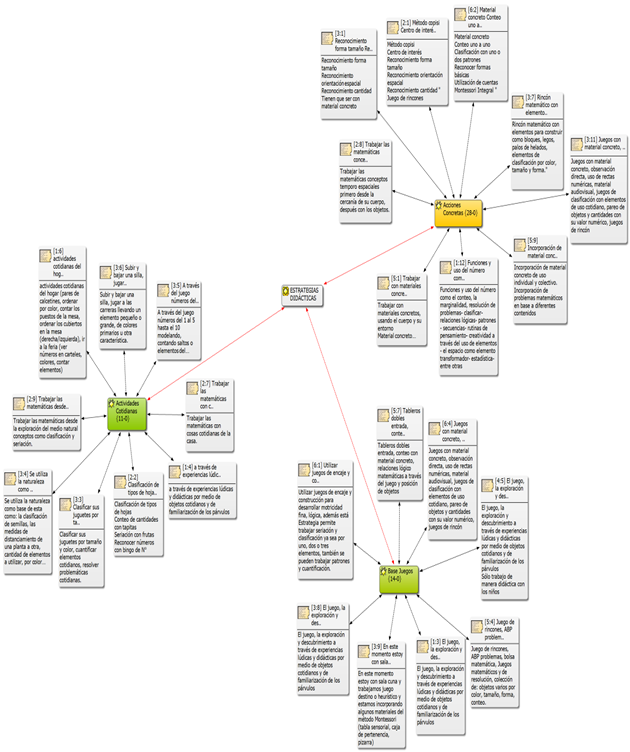
En el estudio se observó de manera preliminar que, por el tipo de institución que brinda el servicio educativo, JUNJI, VTF e INTEGRA presentan la mayor carga de responsabilidad, siendo seguidas por las escuelas municipales, y teniendo menor cuota tanto los colegios particulares subvencionados como los servicios locales. En cuanto al tiempo de servicio, el mayor rango se ubica en quienes tienen más de 18 años de experiencia. En esta misma línea para conocer en profundidad la esencia del fenómeno emergente entre la didáctica de la matemática y el desarrollo de pensamiento matemático en niños de la primera infancia, la información recolectada se presenta en una estructura representativa que describe en gran medida las relaciones emergentes entre la categoría Estrategia Didáctica y las subcategorías Acciones Concretas, Actividades Cotidianas, y Base Juegos. A continuación, se presenta la Figura 1, con la estructura emergente:
Abordar la complejidad de las estrategias didácticas que fomentan el desarrollo del pensamiento matemático en las niñas y niños en Educación Inicial es esencial, ya que a nivel docente es necesario, igualmente, contextualizar, actualizar o desarrollar la competencia didáctica para abordar los encuentros pedagógicos conjuntamente con el fomento del pensamiento matemático. La didáctica de las matemáticas debiese revelarlas como una ciencia útil al ser humano, y, sobre todo, para la generación de formas de pensar y razonar que exigen mayor complejidad y mayor propensión hacia la abstracción, como una forma de resolver problemas propios del entorno humano.
Con el desarrollo de la investigación se generó una aproximación teórica que relacionó las descripciones y las unidades de sentido, a fin de transmitir la esencia de la experiencia en cuanto a pensamiento matemático y la necesidad de una didáctica que sea de gran impacto en las comunidades educativas de las regiones estudiadas.
A partir de las inquietudes y afirmaciones anteriores, se realizó un esfuerzo cognitivo para lograr el propósito de la presente indagación, la cual emerge de la interpretación y análisis de las características esenciales de las categorías apriorísticas Desarrollo del Pensamiento Matemático y Estrategias Didácticas, cuya finalidad se centra en identificar e interpretar las estrategias didácticas que emplean las educadoras de párvulos con el fin de desarrollar el pensamiento matemático en niñas y niños entre 2 y 4 años de edad en las salas de clases.
En este sentido, la categoría Estrategias Didácticas se encuentra constituida por las características esenciales o subcategorías acciones concretas (tal como se observa en la Figura 1), actividades cotidianas, y base juegos; a partir de la concreción de esos tres elementos se puede definir que las estrategias didácticas fomentadoras del desarrollo del pensamiento matemático en estudiantes de Educación Inicial supone, según Feo (2018), "una proyección mental ideal centrada en un propósito académico o de instrucción" (p. 198), que sustentada por aserciones teóricas que definen los procesos de enseñanza y aprendizaje, procuran apoyo en procedimientos y la activación de procesos cognitivos elementales para procesar la información y generar conceptos esenciales que le permitan a la niña y al niño reconocer formas, cantidad y orientación espacial, lo que se agrupa en un pensamiento matemático.
Como Acciones Concretas se pueden definir todas las interacciones y estímulos que el niño alcanza al manipular, explorar y experimentar con objetos, instrumentos o materiales didácticos propios del entorno de la niña o niño. Cabe destacar que la educadora realiza una práctica pedagógica inmediata a situaciones reales que la niña o el niño enfrenta cotidianamente (BCEP, 2018). Este concepto queda descrito a través de las siguientes verbalizaciones de las informantes claves entrevistadas:
P 1: Conteo uno a uno, clasificación con uno o dos patrones, reconocer formas básicas, utilización de cuentas (11:14) Funciones y uso del número, como el conteo, la marginalidad, resolución de problemas- clasificar- relaciones lógicas- patrones- secuencias- rutinas de pensamiento- creatividad a través del uso de elementos- el espacio como elemento transformador- estadística- entre otras (20:20).
P 2: Método COPISI, centro de interés, reconocimiento forma tamaño, reconocimiento orientación espacial, reconocimiento cantidad, juego de rincones (7:12). Clasificar, patrones, manipular objetos, serie, método científico, causa efecto, juego heurístico (18:18). Trabajar las matemáticas, conceptos espacio-temporales, primero desde la cercanía de su cuerpo, después con los objetos (24:24).
P 3: Reconocimiento de forma tamaño, reconocimiento de orientación espacial, reconocimiento de cantidad, tienen que ser con material concreto (5:8). Rincón matemático con elementos para construir, como bloques, legos, palos de helados, elementos de clasificación por color, tamaño y forma (16:16).
P 4: A través de material concreto, con su propio cuerpo (7:8). Método COPISI, esta estrategia es la que más utilizamos a nivel institucional de colegio (20:20).
P 5: Trabajar con materiales concretos, usando el cuerpo y su entorno material concreto para clasificar, agrupar (5:6). Funciones y uso del número como el conteo, la marginalidad, resolución de problemas -clasificar- relaciones lógicas-patrones- secuencias-rutinas de pensamiento-creatividad a través del uso de elementos- el espacio como elemento transformador- estadística- entre otras (22:22).
P 6: Material concreto, conteo uno a uno. Clasificación con uno o dos patrones, reconocer formas básicas, utilización de cuentas, Montessori Integral (6:11). Desarrollarlo con material concreto, pertinente método COPISI, a través desafíos (ABP) (8:8).
El pensamiento matemático refiere al uso de la razón humana, por lo cual el sujeto genera la capacidad de analizar y procesar información captada por los sentidos, y de esta manera, en la medida de su desarrollo cognitivo, le es posible establecer conclusiones, las cuales son vistas como toma de decisiones y acciones en la búsqueda de solucionar una situación problemática o la demanda de una tarea. En la primera infancia (Bautista et al., 2018; Mineduc, 2018) se conforma la base cognitiva para el desarrollo y fortalecimiento del pensamiento, y hay una conexión invariable con las características evolutivas, intereses y necesidades de las niñas y niños.
P 1: Actividades cotidianas del hogar (pares de calcetines, ordenar por color, contar los puestos de la mesa, ordenar los cubiertos en la mesa (derecha/izquierda), ir a la feria (ver números en carteles, colores, contar elementos) (9:9).
P 2: Niños/as protagonistas en la construcción de su aprendizaje (19:19). Trabajar las matemáticas desde la exploración del medio natural, conceptos como clasificación y seriación (25:25).
P3: Clasificar sus juguetes por tamaño y color, cuantificar elementos cotidianos, resolver problemáticas cotidianas (12:12). Se utiliza la naturaleza como base para: la clasificación de semillas, las medidas de distanciamiento de una planta a otra, cantidad de elementos a utilizar, por color tamaño, etc. (13:13). Subir y bajar una silla, jugar a las carreras llevando un elemento pequeño o grande, de colores primarios u otra característica (15:15).A través de actividades cotidianas la niña y el niño interactúan y aprenden, de esto se infiere que dicho accionar didáctico planificado por la docente se encuentra compuesto o sustentado por premisas orientadoras para la recopilación, organización, análisis de situaciones peculiares aprendidas socialmente para generar una toma de decisiones o alguna conclusión (Feo, 2014).
La Base Juegos es toda acción de juego planificada como medio didáctico para que emerja un aprendizaje con significados. El juego (Ponce, 2017; Mineduc, 2018; y González- Moreno, 2018), en otras palabras, es la actividad rectora intencionada con fines didácticos que se emplea para el desarrollo del pensamiento matemático con base en la lúdica, cuyo propósito es activar procesos cognitivos como la abstracción, representación, creatividad y demostración matemática. En este sentido las informantes claves expresan lo siguiente:
P 1: El juego, la exploración y descubrimiento a través de experiencias lúdicas y didácticas por medio de objetos cotidianos y de familiarización de los párvulos (8:8). Juegos diversos para desarrollar el pensamiento matemático (17:17).
P 2: El juego como medio para el aprendizaje (20:20).
P 3: El juego, la exploración y descubrimiento a través de experiencias lúdicas y didácticas por medio de objetos cotidianos y de familiarización de los párvulos (17:17).
P 4: El juego, la exploración y descubrimiento a través de experiencias lúdicas y didácticas por medio de objetos cotidianos y de familiarización de los párvulos Sólo trabajo de manera didáctica con los niños (14:15).
P 5: Tableros dobles entrada, conteo con material concreto, relaciones lógico- matemáticas a través del juego y posición de objetos (20:20).
P 6: Utilizar juegos de encaje y construcción para desarrollar motricidad fina, lógica; además esta Estrategia permite trabajar seriación y clasificación, ya sea por uno, dos o tres elementos, también se pueden trabajar patrones y cuantificación (5:5).
P 7: Todo a base del juego y enfoque Reggio-Emilia (7:7).
Finalmente, el fomento del desarrollo del pensamiento matemático en las niñas y niños de Educación Inicial estimula y da prioridad al razonamiento vislumbrado por los procesos cognitivos como comprensión, análisis, comparación, estimación, imaginación espacial, vistos a su vez como el eje esencial para el propio desarrollo de las competencias matemáticas.
Discusión
De acuerdo a los hallazgos se evidencia que el pensamiento lógico matemático está concebido como un proceso cognitivo e implica desarrollar en el niño y la niña de primera infancia competencias para la adquisición de conocimientos, y no, necesariamente, esta direccionado a los procesos básicos de las matemáticas, sino también es un proceso que permite la evolución de otras áreas de aprendizaje. De allí que Piaget (1991), sostiene que el niño y la niña de acuerdo a su desarrollo aprende a partir de una secuencia lógica, lo que permite la asimilación de los elementos que lo rodean con sus propias estructuras que van dando paso a otros estados evolutivos, por lo tanto el conocimiento lógico matemático surge desde los primeros meses de vida cuando el bebé va teniendo las experiencias al manipular los objetos, lo que permite ir a un progresivo conocimiento del mundo, de lo más simple a lo más complejo.
Por lo tanto, el estudio en el contexto de la Educación Parvularia, logra que niñas y niños desarrollen de la mejor forma su pensamiento matemático, en un ambiente donde la acción docente permite, desde la creatividad, diseñar estrategias didácticas, y utilizar diversas estrategias para solucionar problemas reales, implicando el desarrollo de habilidades, actitudes, valores, y conocimientos útiles y necesarios a partir del trabajo individual o colaborativo, fomentando, a su vez, el razonamiento, el análisis, la apreciación, la imaginación espacial, la asociación, la clasificación, la seriación, y la inclusión, para, así, generar posibilidades para la construcción de conceptos matemáticos que le permitan a la niña y al niño reconocer formas, cantidad y orientación espacial.
Los hallazgos permitieron develar que, aparte de reconocer la necesidad de utilizar estrategias didácticas en matemáticas como fundamento de su especificidad didáctica, es posible lograr un pensamiento matemático amplio y consolidado hacia el desarrollo continuo. Cabe destacar que hay autores que expresan que la mayor dificultad en la enseñanza de las matemáticas en la primera infancia, tiene que ver con las estrategias aplicadas por los docentes (Celi et al., 2021).
De lo anterior se refleja la importancia de considerar que las actividades cotidianas en los ambientes áulicos se encuentran definidas por una serie de procedimientos y operaciones con las que la niña o el niño se encuentran familiarizados y son propios de su entorno social y cultural. El niño nace en un contexto social que lo acobija y lo educa, a través de las costumbres y tradiciones, así como también de las exigencias de ese mismo entorno. De ahí que las actividades cotidianas que conforman parte de las estrategias didácticas fomentadoras del desarrollo del pensamiento matemático en niñas y niños párvulos, son fundamentales y centran su importancia en la sensibilización del niño hacia la utilidad y uso del pensamiento matemático en la vida humana.











 texto en
texto en