Introducción
La enseñanza asume un gran reto en la actualidad y los docentes de América Latina, incluyendo al Ecuador, no escapan de ello. El Proceso de Enseñanza-Aprendizaje (PEA) se viene ejecutando, desde hace algún tiempo, desde otras perspectivas. Se invita a participar de un modelo educativo más interactivo y dinámico, donde los estudiantes se expresan con mayor libertad y creatividad. Debido a ello, el docente debe ser muy proactivo e innovador.
Diversos estudios demuestran que no son pocos los países de América Latina que ven la necesidad de implementar actividades didácticas con calidad para llevar a cabo una buena enseñanza que se traduzca en aprendizajes de excelencia en cada uno de sus estudiantes; uno de estos países es Chile. Los resultados que han alcanzado los estudiantes chilenos en la asignatura Matemática son realmente preocupantes, ya que según la información que proporciona el Sistema de Medición de la Calidad de la Educación (SIMCE), los educandos se encuentran en un nivel medio (Minte et al., 2020). Por lo tanto, se puede entender que Chile necesita mejorar el nivel de calidad de la educación; es decir, desde realizar un análisis sistemático y metódico del nivel de aprendizaje alcanzado de sus estudiantes, hasta la capacitación de los docentes.
Por otra parte, en ciertos estudios Ecuador evidenció dificultades en la asignatura Matemática. En los resultados obtenidos en las pruebas PISA-D 2018, el 70,9 % de los estudiantes no alcanzaron el nivel dos y se ubicaron en un nivel básico. El desempeño promedio fue de 337 puntos (Bernal et al., 2019). Todo esto permite apreciar que Ecuador no ha registrado cambios significativos a favor del Proceso de Enseñanza-Aprendizaje. Es muy probable que los estudiantes enfrenten dificultades cognitivas y procedimentales para resolver problemas de la vida cotidiana asociados a las matemáticas.
La Matemática en todos los niveles educacionales presenta cierta complejidad y rigurosidad. Sin embargo, se pueden tomar decisiones que favorezcan su aprendizaje. Lamentablemente, las evidencias dicen lo contrario. Existen inconvenientes, no se establecen buenos vínculos entre el aprendizaje y la cotidianeidad de los educandos. Inclusive, se ven afectadas sus habilidades críticas y lógicas que no se desarrollan adecuadamente. Para tomar cualquier decisión, es preciso analizar el nivel de conocimiento que presentan los niños. Conociendo mejor la realidad pueden prepararse diversas actividades didácticas que, con toda intención, contribuyan al desarrollo de distintas competencias.
Hay una invitación clara: las matemáticas deben ser analizadas, descifradas y comprendidas como lenguaje universal. Teniendo en cuenta que los aprendizajes y contenidos de esta asignatura en el 6to grado de EGB manifiestan cierta aplicabilidad en la vida cotidiana de los estudiantes: "El maestro o profesor podrá guiar a su alumnado a ver cómo las matemáticas ayudan a comprender situaciones cotidianas y, como consecuencia de ello, a aprender Matemáticas" (Albertí, 2018, p. 20).
Logrando énfasis en el tema de matemáticas del 6to grado, un plano cartesiano se encuentra formado por dos rectas numéricas, una vertical y otra horizontal. Por su parte, la recta horizontal es denominada eje de las abscisas o "X", y el vertical eje de las ordenadas o "Y"; el punto donde se cortan recibe el nombre de origen, respectivamente con un valor de cero. En lo particular un plano cartesiano no solo se simboliza en números, sino que se pueden incorporan una infinidad de cosas.
Por su parte, un par ordenado se encuentra formado por dos elementos, con un orden claramente determinado (X, Y); es decir, que siempre llevan un orden alfabético, incluso puede existir un par ordenado formado por (A, B). En relación a su procedimiento, se debe situar primero el componente del eje X y luego el componente del eje Y, formando un par ordenado en el plano cartesiano.
Una vez establecido el plano cartesiano y par ordenado, es necesario referirnos al aprendizaje, porque es un proceso que nos permite adquirir habilidades, conocimiento, actitudes y valores. Además, teniendo en cuenta que el aprendizaje se desarrolla durante toda la vida; es decir, que siempre hay algo nuevo que aprender.
Por otra parte, es necesario tener en cuenta los estándares que deben sostener una educación de calidad. Dichos estándares representan los contenidos y procesos matemáticos con los que el estudiante debería formarse, propiciándoles algo más práctico que teórico. El hecho de que no se desarrolle una matemática de calidad y con énfasis en la práctica, es por los lastres que acarrea la educación tradicional, en la cual los estudiantes son receptores de información, memoristas, mientras el docente protagoniza la actividad con mucha autoridad.
Además, se estimula la educación bancaria entendiendo los contenidos que domina el maestro como depósitos valiosos que, instalados en la cabeza de los estudiantes, tienen que repetir textualmente. Con estas influencias se devela un rechazo por parte de los docentes a lo nuevo, a lo innovador. Dando a entender que no existe un progreso real significativo en la educación ecuatoriana, el aprendizaje no es memorización; el aprendizaje es comprensión.
Si se quiere formar seres capaces de implementar lo aprendido en la vida cotidiana, es necesario aplicar diferentes metodologías; por ejemplo, el aprendizaje por descubrimiento, donde el docente fomente las prácticas investigativas en los estudiantes, teniendo en cuenta sus necesidades e intereses. El aprendizaje por descubrimiento se basa en que sus estudiantes creen su propio conocimiento y se adueñen del mismo, generando así un aprendizaje activo y práctico.
El aprendizaje significativo es importante, muy alentador y beneficioso. Relaciona los conocimientos nuevos con los conocimientos que ya posee el estudiante; conocimientos previos. Por tal motivo, con el aprendizaje significativo el estudiante será capaz de construir su propio conocimiento, en el sentido de que aprende, investiga y es capaz de resolver problemas de su vida cotidiana. No obstante, es indispensable que el docente se involucre con sus educandos, escuchándolos y dialogando con ellos, y a partir de eso guiarlos en su proceso.
La Didáctica no puede faltar en el trabajo del docente, ni dentro ni fuera del contexto educativo. Cuando funciona didácticamente la clase se hace muy efectivo la selección y el manejo de diversos medios y el lenguaje que, con calidad y eficacia, contribuyen al progreso y desarrollo de varias competencias. Por su parte, Enríquez et al. (2018) considera que el docente es el eje principal para que se dé el Proceso de Enseñanza-Aprendizaje, y que durante su formación debe de ser de gran interés el estudio de la didáctica general para alcanzar la construcción de nuevas experiencias.
Los principios didácticos son faros que iluminan los rumbos en el quehacer docente. Resultan una guía vital para que se ejecute el Proceso de Enseñanza-Aprendizaje. Favorecen la selección de medios de enseñanza y humanizan la evaluación. Según Cano de la Cruz (2021): "La ontología de estos principios se enfoca más en el hecho educativo, es decir, más en la Pedagogía que en la Didáctica, lo cual no le resta significatividad y aporte" (p. 24).
Las funciones didácticas del docente favorecen que desarrolle la clase de forma activa y se logre un aprendizaje de calidad; son vitales en la organización de la enseñanza y el aprendizaje. Al tratar nuevos contenidos, y en clases de reafirmación, es importante que prevalezcan procedimientos que garanticen un ambiente agradable desde la actitud positiva del docente. Esto influye en el desarrollo de nuevas habilidades que aportan al crecimiento del estudiante; además, en la asignatura Matemática es preciso fomentar un pensamiento lógico que evolucione sistemáticamente frente a los problemas que se presentan en la cotidianeidad.
Regresando la Didáctica, es muy favorable que el docente conozca a cada estudiante. Las actividades se formulan en función de las características individuales de cada uno de ellos. Debemos entender esta gestión como un proceso sistemático y ordenado para alcanzar las metas propuestas en el desarrollo de los contenidos. Para el desarrollo de las actividades, según sus características y en dependencia de los contenidos a tratar, se pueden organizar a los niños de forma grupal o en trabajo independiente.
Una de estas estrategias es el juego. Permite, en función de los objetivos y contenidos, plantear actividades que favorezcan los procesos de aprendizaje de cada uno de los estudiantes. Por lo tanto, el juego ayuda en la construcción de un ambiente adecuado, integral, provechoso y efectivo; es decir, para el desarrollo de conocimientos, para fundamentar el compañerismo, la sociabilidad y el respeto por los demás. El juego, como estrategia didáctica, fortalece varias capacidades en los estudiantes y en los docentes, así como lo mencionan Tamayo y Restrepo (2017): "El juego se convierte en un escenario que toma gran importancia en los procesos de enseñanza y aprendizaje, ya que, debido a su componente lúdico, se transforma en una estrategia altamente motivante para la participación de los sujetos y en las diferentes actividades que se propongan" (p. 112).
Por tanto, proponer actividades efectivas para el aprendizaje de las Matemáticas es un reto constante del contexto educativo actual. Han de permitir el desarrollo de varias destrezas y poner en práctica el pensamiento lógico. Todo esto permite analizar y resolver problemas de la vida, en el escenario que viven los implicados. "Los conceptos lógico matemáticos constituyen un instrumento fundamental y útil, porque a través de estos los niños expresan cada día sus conocimientos en cada una de las experiencias de formación educativa" (Lugo et al., 2019).
Para la estructura de una actividad didáctica deben considerarse algunos aspectos fundamentales. Tener presente el objetivo que alcanzarán los estudiantes y su aplicabilidad en la vida cotidianeidad es muy importante. Por tal motivo, es preciso conocer y analizar los conocimientos que ya sabe el niño. Esto permitirá identificar desde qué punto se debe iniciar. Así lo menciona Cano de la Cruz (2021): "Siempre se debe partir de cuáles son sus conocimientos previos, para detectar lo que no sabe y fundamentar el aprendizaje sobre lo que conoce, y partir de la idea de que el alumno comprenderá mucho mejor aquello de lo que tiene una idea previa" (p. 156).
Se enriquecen los conocimientos previos con el nuevo conocimiento, pero es importante orientar a los estudiantes hacia el qué, el cómo y para qué van a aprender sobre lo propuesto. De esa forma evoluciona la nueva visión de su aprendizaje. Incluso el rol del docente consiste en conocer a los estudiantes, saber qué saben, quiénes son, qué necesitan y corresponder a su Proceso de Enseñanza-Aprendizaje. Por tanto, preferiblemente las actividades deben ser interactivas, dinámicas y una propuesta ante las necesidades e intereses de los estudiantes. Finalmente, el docente debe verificar si el objetivo propuesto para la actividad fue conseguido.
Analizar el nivel de conocimiento que tienen los estudiantes de 6to grado de EGB permitirá el diseño de actividades didácticas pertinentes a favor de su aprendizaje. No deben perderse de vista la motivación, las relaciones interpersonales y la vida cotidiana. El juego didáctico puede favorecer, en gran medida, teniendo en cuenta que para los niños es tan importante el juego como para los adultos el trabajo.
Materiales y métodos
El presente trabajo de investigación se desarrolló desde un enfoque cuantitativo. El enfoque cuantitativo, desde la visión de Gómez (2006): "Utiliza la recolección y el análisis de datos para contestar preguntas de investigación y probar hipótesis establecidas previamente, y confía en la medición numérica, el conteo, y en el uso de la estadística" (p. 70). Por otra parte, se desarrolló bajo un diseño no experimental. Gómez (2006) menciona que: "Se deben observar los fenómenos tal y como se dan en su contexto natural, para después analizarlos" (p. 60). Es decir, que se realizó sin manipulación de variables.
Además, el estudio tiene un carácter descriptivo. Gómez (2006) establece que: "La información necesaria para el análisis está constituida por la distribución de frecuencias, medidas de tendencia central y las medidas de variabilidad" (p. 140); resumiendo, para esta investigación la aplicación de la estadística, la medición numérica y análisis porcentual, desde un diagnóstico que permita describir el estado del conocimiento del grupo.
La población se consideró de 15 estudiantes entre niños y niñas organizados en el único grupo de 6to grado de EGB de la Unidad Educativa "Julio Moreno Espinosa". Según Hernández et at. (2010) define como "Población o universo al conjunto de todos los casos que concuerdan con determinadas especificaciones" (p. 174). La muestra fue constituida por el 100 % de la población. Se seleccionó de forma no probabilística por conveniencia del estudio. Cabe mencionar que una muestra es comprendida como subconjunto de la población a la cual se va a enfocar la investigación.
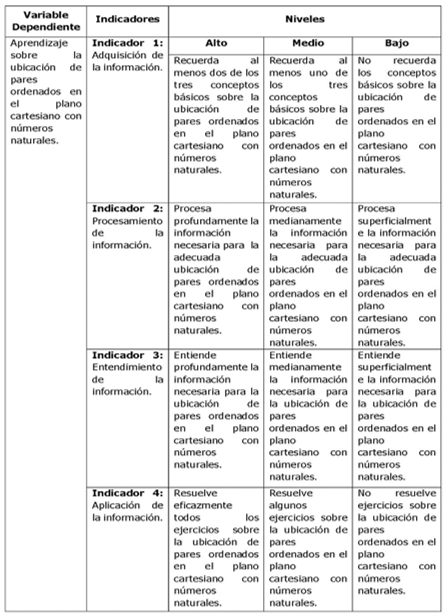
La variable dependiente (Tabla 1), considerada para esta investigación, es el aprendizaje sobre la ubicación de pares ordenados en el plano cartesiano con números naturales. Según Espinoza (2018), afirma que: "Constituyen los efectos o consecuencias que dan origen a los resultados de la investigación" (Rev.). A partir de su análisis se establecieron cuatro indicadores y tres niveles de conocimiento: alto, medio y bajo.
Por otra parte, se aplicó la estadística descriptiva. "La estadística descriptiva es la rama de la estadística que formula recomendaciones de cómo resumir, de forma clara y sencilla, los datos de una investigación en cuadros, tablas, figuras o gráficos" (Rendón et al., 2016). Además, se empleó el paquete estadístico SPSS. Para Rivadeneira et. al (2020) esta herramienta es usada en casi todas las ramas de la ciencia, logrando enfatizar su utilidad en la cuantificación de datos, además su fácil comprensión.
Resultados
Nivel de conocimiento
Los análisis que a continuación se hacen permiten describir el nivel de conocimiento que presentan los estudiantes de 6to grado EGB. Garcés et al. (2018) mencionan que: "Los conocimientos crean puentes que atraviesan el proceso de asimilación para que la nueva información se convierta en un instrumento potencialmente significativo, para trascender en el sentido de aprender a aprender" (p. 5).
Con respecto a este indicador (Tabla 2), se evidencia que el 26,7 % alcanza un nivel de conocimiento alto. Significa que cuatro estudiantes recuerdan al menos dos de los tres conceptos básicos evaluados. No obstante, el 13,3 %, dos alumnos, se manifiestan en un nivel bajo. Quiere decir que no se acuerdan de ningún concepto. Esto puede influir negativamente en la asimilación de otros contenidos durante la asignatura de Matemática en el actual curso y en niveles posteriores. Finalmente, un 60 %, el mayor porcentaje, se encuentran en un nivel medio de conocimiento. Ello declara que sí recuerdan la información básica necesaria para resolver ejercicios vinculados con el tema en cuestión.
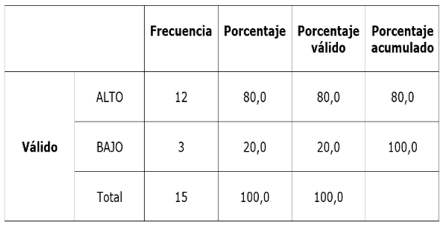
Como se puede apreciar (Tabla 3), en este caso, el 80 % de los estudiantes logra un nivel de conocimiento alto. Resulta significativo y alentador que 12 estudiantes procesen de forma concreta la información necesaria para la resolución de problemas asociados a estos temas que son de vital importancia, al menos, para la vida escolar. Sin embargo, el 20 %, tres estudiantes, se ubica en un nivel bajo. Quiere decir que no asimilan o asimilan superficialmente la información para ubicar correctamente los pares ordenados en el plano cartesiano con números naturales.
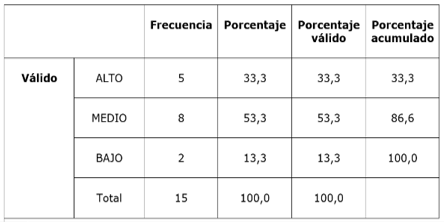
En el análisis sobre el entendimiento de la información (Tabla 4), hay cinco estudiantes, el 33,3 %, que muestran un alto nivel de conocimiento. Dicho de otra forma, logran entender muy bien la información necesaria para la acertada resolución de ejercicios sobre las temáticas de interés a favor de su vida cotidiana. Por el contrario, el 13,3 % se muestran en un nivel bajo. En otras palabras, tienen problemas en el entendimiento de la información, presentando inconvenientes con el aprendizaje durante el presente curso. Por otra parte, con el mayor porcentaje de estudiantes, el 53,3 % de los evaluados se ubican en el nivel medio. Se pudiera decir que ocho estudiantes sí entienden, pero poco, sobre la ubicación de pares ordenados en el plano cartesiano con números naturales.
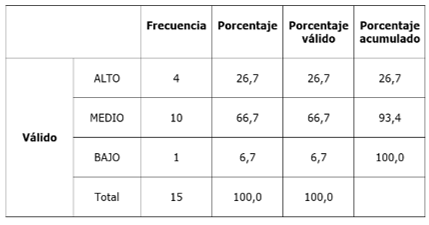
Al aplicar la información (Tabla 5), solo cuatro estudiantes, el 26,7 %, logran hacerlo con mucha eficacia y se ubican en un nivel alto. Lograron resolver adecuadamente los ejercicios sobre la ubicación de pares ordenados en el plano cartesiano con números naturales, por lo que tienen importantes habilidades para gestionar y solucionar problemas de la vida cotidiana. Lamentablemente, un estudiante, que representa el 6,7 %, muestra un bajo nivel de conocimiento. Es decir, que tiene pocas habilidades para la resolución de los ejercicios planteados. Si no se trabajan sistemáticamente estos temas en clases puede que arrastre estas dificultades a los niveles superiores. En el nivel medio se aprecia un 66,7 %, con el mayor porcentaje. Un total de 10 estudiantes, la mayoría, son quienes pueden resolver solo algunos ejercicios sobre estos temas de matemáticas vinculados con la vida cotidiana.
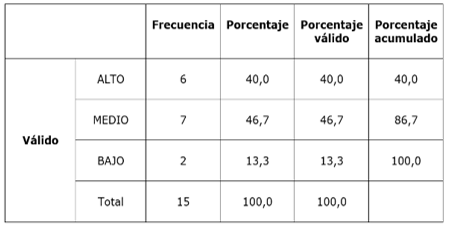
Desde una visión más holística (Tabla 6), se aprecia que seis estudiantes, el 40,0 %, se encuentra en un nivel alto de conocimiento. Ello refleja que tienen dominio teórico sobre el tema y pueden resolver diversos problemas de la vida cotidiana relacionados con estos contenidos. Con quienes más hay que trabajar es con el 13,3 %, dos estudiantes, que se ubican en un nivel bajo. Dichos alumnos posiblemente tengan dificultades para aprender en niveles superiores, que precisan de estas bases como prerrequisitos. El 46,7 % de los estudiantes se encuentran en un nivel medio y constituye la mayoría. Logran un nivel básico sobre la ubicación de pares ordenados en el plano cartesiano con números naturales. Para que los estudiantes que se encuentran en los niveles bajo y medio avancen al nivel alto es preciso que la propuesta de actividades considere las falencias que más afectan el aprendizaje sobre los temas tratados. Sin que la negatividad ciegue los ojos del educador, preocupa que estos estudiantes, lejos de evolucionar, retrocedan.
Actividades didácticas
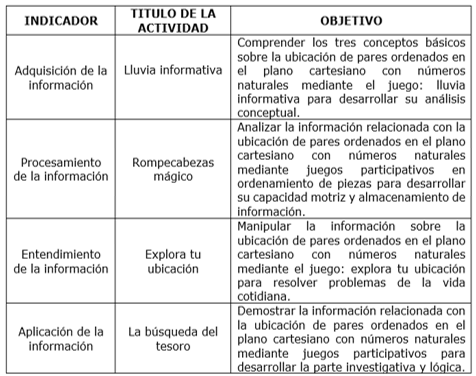
Es necesario proponer diez actividades que favorezcan el aprendizaje de los estudiantes de 6to grado EGB, con relación a cada uno de los indicadores. Mediante las actividades es posible desarrollar el tema de forma más activa, dinámica y se establecen relaciones con la vida cotidiana. Cada actividad se vincula con juegos didácticos. En la siguiente tabla 7 hay una muestra de cuatro actividades que responden a cada indicador (adquisición, procesamiento, entendimiento y aplicación), respectivamente. Mediante el código QR o enlace que se muestra, se logrará visualizar el resto de las actividades de forma más explícita.
Discusión
Se determinó el estado del conocimiento y se logró evidenciar que los estudiantes se encuentran en un nivel medio de conocimiento. Garcés et al. (2018) consideran que se puede determinar el nivel en base a la información obtenida y recibida de forma trascendental y durante un período concreto. En menor medida, hay dificultades en la adquisición de información para dominar los conceptos fundamentales. Lo más alarmante se presentó a la hora de la resolución de ejercicios, considerando que esta es la fase de aplicación.
De tal forma, se proponen 10 actividades didácticas sobre la ubicación de pares ordenados en el plano cartesiano con números naturales. Las actividades son necesarias y ventajosas al momento de desarrollar su aprendizaje y generar nuevas experiencias; para ello se tuvo en cuenta cada uno de los indicadores. Además, se consideró al juego por lo favorable que puede ser para el aprendizaje sobre estas temáticas. Según Tamayo y Restrepo (2017), el juego es de gran importancia en el Proceso de Enseñanza-Aprendizaje, convirtiéndose así en una estrategia motivante para los educandos, que los lleva a alcanzar una mayor participación.
Una investigación realizada por Cuesta en Colombia reafirma que el juego es un factor importante en el desarrollo de contenidos académicos e interacción entre sus semejantes, incluso también ayuda a alcanzar un aprendizaje significativo en los estudiantes.
Esta propuesta de actividades tiene un carácter formativo: permitir el adecuado desarrollo del pensamiento lógico y crítico, haciendo énfasis en situaciones estrechamente vinculadas con la vida cotidiana de los estudiantes. Según Albertí (2018), menciona que: "Dos aspectos fundamentales relacionan las matemáticas con la vida: su utilidad y ayuda a la comprensión" (p. 18). Es decir, que es importante desarrollar los procesos adecuados para logara comprender a las matemáticas como un área del conocimiento valioso e importante en su día a día.
Además, en palabras de Lugo et al. (2019), el desarrollo lógico-matemático es útil y básico; mediante él los estudiantes experimentan y adquieren conocimientos diariamente. Otra de las metas de la propuesta es contribuir a que se adquiera una visión más amplia sobre cómo aprender y cómo enseñar matemáticas de forma dinámica. Siempre reflexionando sobre los objetivos que propone el currículo y el análisis de los contenidos necesarios para vencerlos.
Por tanto, los estudiantes muestran dificultades en la adquisición de información y resolución de ejercicios, y pueden surgir inconvenientes para el aprendizaje sobre temas muy importantes que se apoyan en la ubicación de pares ordenados en el plano cartesiano con números naturales. De este modo, las actividades didácticas propuestas son el resultado de una profunda reflexión sobre las falencias y potencialidades de los estudiantes, considerando siempre los temas de interés para esta investigación y la importancia de una formación que responda a las necesidades actuales de la sociedad.











 texto en
texto en