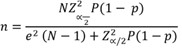Introducción
En el siglo XXI se experimentan profundos cambios en el Proceso de Enseñanza-Aprendizaje (PEA), acrecentados por el desarrollo tecnológico (Sánchez et al., 2020). Las sociedades se caracterizan por estar más conectadas, con más información, más publicaciones y con mayor diversidad en todos los ámbitos de la vida (Solórzano, E. et al., 2020). Este panorama reta a la Universidad, encargada de formar profesionales, a redimensionar la manera de enseñar, por su relación directa con las nuevas posibilidades que permiten el acceso y el uso de tecnologías en la autogestión del aprendizaje para la preparación del docente y del estudiante, en correspondencia con los cambios actuales.
Estudiosos como: Bonet et al. (2018); Leyva & Lariot (2019) Zae et al. (2020); Metaute et al. (2020) particularizan y definen la autogestión del aprendizaje e introducen procedimientos, estrategias y tecnologías que apoyan este proceso. Por otro lado, Sánchez et al. (2020) valoraron la disponibilidad de computadoras con fines educativos en los hogares europeos, latinoamericanos y de manera particular en Cuba, donde se continúa en progreso; pero la realidad cubana con un bloqueo impuesto hace más de 60 años, unido a la crisis provocada por la pandemia por COVID-19 impide en gran medida su avance. Como consecuencia, no todas las personas matriculadas en la Educación Superior poseen las tecnologías necesarias, en el sentido amplio de la palabra, para poder realizar sus estudios universitarios, a pesar de los ingentes esfuerzos del Estado cubano en la informatización de la sociedad y en su transformación digital. Por tanto, es necesario reflexionar sobre el diseño del Proceso de Enseñanza-Aprendizaje con los medios a utilizar, teniendo en cuenta la brecha digital (disponibilidad de acceso y uso de tecnología en todos los sectores de la sociedad). Se impone la búsqueda de alternativas que contribuyan a superar esta realidad, para que todos los estudiantes interesados y con la capacidad intelectual necesaria tengan acceso a la esencialidad del contenido a estudiar, con un incremento en la autogestión del aprendizaje. De esta manera, se puede contribuir a alcanzar una educación para todos y sin excepción.
Con la masificación de la educación en Cuba, en los centros adscriptos al Ministerio de Educación Superior se han incluido carreras que se estudian en la modalidad a distancia o en cursos por encuentros, como es el caso de Contabilidad y Finanzas. El Centro Universitario Municipal (CUM) de Jagüey Grande, Matanzas, la oferta y posee como disciplina Métodos Económicos Matemáticos, donde se incluye la asignatura Matemática Superior I. Sobre el Proceso de Enseñanza-Aprendizaje del cálculo diferencial, temática central en esta asignatura, se han realizado múltiples investigaciones, reconociéndose sus particularidades, su contribución al desarrollo del pensamiento matemático y lo difícil de su comprensión si no se utilizan los métodos adecuados. Naveira & Valdivia (2022) afirman que estos últimos son importantes para arribar a contribuciones teóricas sobre las exigencias de este proceso para la Educación Superior, particularmente para carreras como ingenierías u otras centradas en la administración, pero no indican cómo debe transcurrir la dirección de estos contenidos y no refieren la importancia de las funciones que se atribuyen a la dirección del proceso.
Los planteamientos anteriores tienen su concreción también en el estudio realizado por la autora con encuestas y entrevistas a estudiantes y docentes de la misma en varios municipios de la provincia, donde la presenta como una de las asignaturas más difíciles para estudiar de manera independiente, debido al nivel de abstracción, razonamiento lógico y habilidades que la misma exige en la realización de sus tareas. Todo ello se redimensiona al expresar que el gran desafío de los que enseñan Matemática a distancia se apoya en tres aspectos fundamentales: las características tecnológicas de soporte; la presencia y desempeño del docente en cuanto a asistirlo en su proceso de aprendizaje y la elaboración de materiales que ofrezcan un acceso a los conceptos.
Sobre la afirmación anterior se indagó en el proceso investigativo. Los docentes aluden a su deficiente preparación teórico-metodológica para enfrentar el proceso de enseñanza-aprendizaje en esta asignatura, por la alta utilización de los medios tecnológicos y las dificultades por la insuficiente o nula disponibilidad de recursos tecnológicos. Por otra parte, se estudiaron tesis de maestría y doctorado defendidas en Cuba, lo que permitió valorar que son pocas las que poseen como objeto de estudio la enseñanza de la Matemática en la Educación Superior. Todas abordan un contenido en particular, pero no desde la concepción del Proceso de Enseñanza-Aprendizaje de esta ciencia con una mayor semipresencialidad, proceso con características peculiares y en el que la autogestión del aprendizaje es decisiva.
Al revisar la bibliografía internacional se presenta la misma situación que en las investigaciones cubanas, en las que se destacan: Faustino et al. (2019); González et al. (2018); Radovic et al. (2018), entre otros. Se percibe que, aunque estos autores aportan un conjunto de elementos fundamentales a tener presentes durante el proceso, no se formula un sistema de fundamentos, principios y leyes que describan el desarrollo del Proceso de Enseñanza-Aprendizaje de la Matemática en la Educación Superior en esta modalidad y no se estudian los elementos anteriores para la educación a distancia y lo concerniente a la autogestión del aprendizaje en ella. La mayoría de los casos se mantienen al margen, al estudiar de manera fragmentada algunas situaciones o casos en particular.
Las investigaciones en Matemática sobre el tema de la autogestión del aprendizaje a través del uso de las Tecnologías de Información y las Comunicaciones (TIC), van más destinadas al estudio de la autogestión del conocimiento; ejemplo de ello lo constituye los estudios realizados por Calcines et al. (2017), o el uso de las TIC por Medina et al. (2018), pero no van dirigidas a cómo el uso de las TIC repercutirá en la autogestión del aprendizaje.
Es por ello imprescindible solventar esta situación e ir a la búsqueda de fundamentos teóricos más precisos para la semipresencialidad en el Proceso de Enseñanza-Aprendizaje de la Matemática Superior y, con ello, al análisis de nuevos recursos didácticos, que promuevan el "aprender a aprender Matemática", el desarrollo de tareas docentes que lleven a la actividad independiente del estudiante y que faciliten su proceso de aprendizaje, para lo que es importante tener en cuenta las relaciones del estudiante con el objeto de aprendizaje y otorgarle al docente una función orientadora y mediadora.
A partir de los antecedentes teóricos planteados, se necesita un claustro universitario y estudiantes que asuman el Proceso de Enseñanza-Aprendizaje (PEA) en esta modalidad para esta disciplina, por lo que constituye una necesidad la preparación de los mismos y exige un trabajo científico-metodológico intencionado a las características de la semipresencialidad y al entorno del centro universitario. La revisión bibliográfica realizada, así como las entrevistas a los directivos y docentes de distintos Centros de Educación Superior (CES) del país, apuntan a la no existencia de investigaciones que tributen a los elementos planteados. En Cuba, se ofrecen materiales didácticos como: libros de texto (los mismos de la enseñanza presencial), programa con el plan temático, programa analítico y los objetivos de cada asignatura, cuadernos de ejercicios y guías de estudio, videos y actividades en plataforma Moodle, pero no siempre están orientados a que el estudiante se autogestione su conocimiento. Aun así, es insuficiente la disponibilidad de recursos didácticos, teniendo en cuenta las limitaciones que poseen con el acceso a las tecnologías y la deficiente preparación de los docentes para enfrentarla con calidad, elementos que se obtienen de la aplicación de encuestas, entrevistas, revisión de los documentos metodológicos, entre otros.
En correspondencia con las normativas del país, el Centro Universitario Municipal (CUM) de Jagüey Grande implementa la semipresencialidad en la carrera Contabilidad y Finanzas. Sus especificidades la hacen muy compleja porque su aplicación depende, en gran medida, de las tecnologías y de la preparación del docente para enfrentarla. Se trabaja por desarrollar una educación para todos con los beneficios de la Universidad cubana, como parte de una educación continua y para la vida.
Teniendo en cuenta la existencia de orientaciones en la asignatura Matemática, apremia un estudio que asegure egresados a la altura de estos tiempos y que contribuya a solucionar las deficiencias detectadas. Es precisamente el objetivo del presente trabajo mostrar los resultados del diagnóstico efectuado, que permitió estructurar un resultado científico para minimizar las dificultades. En correspondencia, se aplicaron métodos y técnicas que permitieron el diagnóstico de la situación actual; entre ellos se destacan: el análisis-síntesis, el histórico-lógico, el inductivo-deductivo, el análisis documental y encuestas y entrevistas.
Dentro de las tendencias de desarrollo a nivel mundial aparece el robustecimiento de la semipresencialidad. El estudio de los antecedentes históricos permitió alegar que en Cuba se organizó primeramente en: cursos para trabajadores, vespertinos, nocturnos, por encuentro, dirigidos; orientados fundamentalmente al trabajo independiente y la autopreparación. Se apoyaba en materiales didácticos escritos auxiliados por medios audiovisuales como la televisión educativa, radio, audio-casette y la prensa escrita. Surgió como un modelo de desarrollo mixto en los propios centros de Educación Superior, vinculando la educación semipresencial con la educación presencial.
En la semipresencialidad está presente el aprendizaje autónomo a través de la gestión y autogestión del aprendizaje, en la que el PEA se distingue por la separación del docente y el estudiante en tiempo y espacio. Se apoya en el empleo de diferentes recursos educativos que permitan la adaptabilidad a las necesidades cognitivas y ritmo de aprendizaje de los estudiantes, así como la comunicación multidireccional entre los diferentes actores del proceso de formación. Para su desarrollo es fundamental la labor tutorial, como se expresa en el Reglamento de organización y trabajo metodológico de la Educación Superior en Cuba.
El Ministerio de Ciencia, Tecnología y Medio Ambiente (CITMA) expresa que la gestión del conocimiento es el conjunto de procesos y herramientas que permiten la integración sistémica de acciones para el aprovechamiento y utilización del conocimiento, la información y la experiencia acumulada en el desarrollo cualitativo de una organización. En este mismo documento aparece que, para una correcta gestión del conocimiento, es necesario que se vinculen eficientemente los siguientes elementos: adecuada gestión de la información, uso apropiado e intensivo de las tecnologías de información, enfoques novedosos de la práctica de la comunicación, correcta y moderna gestión de los recursos humanos.
La gestión del conocimiento, frecuentemente, se encuentra relacionada a la obtención de información, con la habilidad individual o colectiva para generar, difundir, compartir y utilizar el conocimiento a partir de la asimilación de la información que se transfiere en forma de conocimiento y se transforma en experiencia de individuos; lo que permite la aplicación del conocimiento. Ello corrobora la importancia de que cada individuo autogestione su conocimiento para contribuir de manera activa a esas transformaciones.
La autogestión se clasifica como un proceso integral de fortalecimiento organizativo, secuencia en las acciones y una capacitación continua, que es robustecer las propias capacidades antes, durante y después de la entrega del bien adquirido, descubriendo las capacidades, destrezas, habilidades individuales y directivas de un grupo de la población. La autogestión se revela en el contexto del desempeño profesional pedagógico y personal del docente a partir de la planificación de las acciones de apropiación, ejecución y autoevaluación, donde se evidencian las interrelaciones: estudiante-docente, docente-docente, docente-sociedad. Cuando el docente busca activamente la información que necesita, es capaz de reflexionar, valorar, elaborar de manera personal la información que obtiene y de articularla con la que posee; de la misma manera, utiliza las operaciones intelectuales en la elección de alternativas de comportamiento y en la estructuración de las respuestas de las distintas situaciones y exigencias del medio.
Aparece de forma evidente la idea del estudio independiente, de ser autodidacta, lo que supone un alto grado de interés y compromiso, de responsabilidad, que debe planificar y organizar su tiempo para responder a las exigencias del curso que sigue y desarrollar la voluntad para el estudio sistemático, lo que se identifica como autogestión del aprendizaje.
La autogestión del aprendizaje es la acción de activar y mantener sistemáticamente procesos metacognitivos, motivacionales, afectivos y conductuales, con el fin de alcanzar objetivos de aprendizaje, en un contexto en particular (Zimmerman, 2008). Implica cuatro fases distintivas: planificación, seguimiento, control y evaluación, en las cuales el individuo debe identificar sus propias necesidades de aprendizaje, establecer sus propios objetivos de aprendizaje, realizar búsqueda de recursos (incluyendo instructores, compañeros y materiales), elegir e implementar sus propias estrategias y métodos de aprendizaje y realizar actividades de evaluación de los resultados.
La capacidad de autogestión del aprendizaje es importante y pertinente en la educación, porque este factor activo en el sujeto aprendiz es el que permite lograr el "aprender a aprender", implicando que la persona sea capaz de trabajar en equipo, de comunicarse asertivamente, de aprovechar su participación en grupos heterogéneos u homogéneos, de comportarse con ética y sensatez en colectividad y de compartir sus conocimientos. Se coincide con las definiciones expresadas y se aporta que la autogestión del aprendizaje y con ello la del conocimiento, son actividades que los sujetos realizan por ellos mismos de manera activa. Proceso centrado en el estudiante, principal protagonista; es decir, menos dependiente de un docente o facilitador, gestor de su formación.
En el año 2002 se producen cambios en la Educación Superior, considerada la reforma universitaria de mayor alcance, al proponerse garantizar el pleno acceso de la población a los procesos universitarios, a través de la creación de los centros y filiales universitarias en los municipios. Estas transformaciones en la educación deben llevar a un replanteamiento de los métodos de enseñanza y de aprendizaje que procuren una mayor flexibilidad, donde "aprender a aprender" sea la clave para lograr que el estudiante alcance la madurez cognitiva necesaria dentro de una nueva cultura de la autoformación, desarrollando hábitos que lo hagan intelectualmente más autónomo (Mendo et al., 2022).
Las instituciones universitarias ofrecen materiales didácticos, pero generalmente son los que se utilizan en la enseñanza presencial, sin la necesaria adecuación a esta modalidad de estudio, por lo que es insuficiente la disponibilidad de recursos didácticos, digitales e impresos para el proceso de autogestión del aprendizaje y, en particular, en la enseñanza-aprendizaje de la Matemática Superior. Además, persisten insuficiencias en el PEA a distancia que justifican la necesidad de preparación del docente y del estudiante para asumir el reto. Lo anterior hace reflexionar sobre el trabajo científico-investigativo y profesional, porque aún no cubre las necesidades de impacto y pertinencia social que se correspondan con las problemáticas de la semipresencialidad. Esto implica lograr una mayor calidad en la educación, por lo que se hace necesario que los docentes alcancen un nivel de desarrollo profesional que les permita aplicar prácticas didácticas más efectivas a los problemas pedagógicos que esta modalidad genera en el actuar diario y perfeccionar la actividad docente y la efectividad en el trabajo metodológico. Para obtener estos resultados, es indispensable perfeccionar las estrategias didácticas a la hora de ofrecer sus consultas, contribuyendo a que el estudiante sea capaz de autogestionarse su aprendizaje, aun en condiciones mínimas del uso de la tecnología.
Finalmente, se requiere, por tanto, la gestión de acciones necesarias para lograr los objetivos que se propone la carrera Contabilidad y Finanzas, la que exige de la modalidad a distancia ocupar un lugar esencial tanto en el proceso pedagógico como en el desarrollo del territorio. El trabajo de la Universidad debe tener en cuenta el perfeccionamiento del PEA, con el accionar de todos los factores propios de este proceso, mediante un modelo pedagógico flexible y adecuado a las características de los estudiantes, de manera que se potencie la independencia y el esfuerzo personal.
Es por ello que el presente artículo tiene como objetivo: mostrar los resultados del diagnóstico efectuado, que permita estructurar un resultado científico para minimizar las dificultades detectadas.
Materiales y métodos
El proceder metodológico de la investigación tiene sus bases en el método dialéctico-materialista como metodología general para el análisis e interpretación de los problemas sociales, así como es guía para la transformación de la sociedad. Se utilizaron como métodos y técnicas de investigación del nivel teórico: el análisis-síntesis, que se aplicó en el proceso de revisión bibliográfica y otros documentos pertinentes como el Plan de estudio E y la Resolución No. 47/22 (MES, 2022); el método histórico-lógico, en el estudio de las tendencias que han destacado los momentos esenciales de su propia evolución por el que ha transitado la semipresencialidad, mediante el análisis de los antecedentes históricos y diferentes modos concretos de manifestación del problema estudiado como: las necesidades de preparación y habilidades de docentes y estudiantes para asumir el PEA de la Matemática Superior I de esta forma; el método inductivo-deductivo, empleado para la fundamentación del problema de investigación y la propuesta de solución, así como lograr la generalización del estudio y la posibilidad de la implementación una alternativa didáctica.
Los métodos empíricos se utilizaron para constatar y fundamentar el problema de investigación, así como para evaluar y caracterizar el comportamiento de las dimensiones que componen la variable de la investigación. Entre ellos se encuentran: las encuestas a estudiantes, para constatar el nivel de conocimientos sobre el desarrollo de la semipresencialidad en el PEA, destinada a obtener datos acerca de las necesidades de preparación en la asignatura Matemática Superior I; la entrevista a docentes de la Matemática en la Universidad de Matanzas, dirigida a conocer los procedimientos que utilizan para contribuir a la autogestión del aprendizaje y enseñar la Matemática Superior I. En el análisis de documentos se utilizaron, como documentos importantes: el Programa de estudio E, documento rector del PEA y la Res No. 47/22, preparación de clases de docentes, materiales docentes elaborados, documentos en plataformas interactivas, evaluaciones de los estudiantes, planes de trabajo metodológico, evaluaciones profesorales, entre otros, para estudiar la situación real y deseada de la variable.
En el caso de los docentes, se trabajó con los CUM de la provincia en los que se imparte la carrera en condiciones de semipresencialidad, al considerar que, en el CUM de Jagüey Grande, Matanzas, solamente trabajan un docente y la autora. La experiencia previa de los docentes en la dirección de este proceso a distancia es poca, pues el 25 % (dos docentes) la han impartido en esta modalidad cinco veces, otro 25 % dos veces y el 50 % una vez o nunca. Si se tiene en cuenta que la experiencia contribuye al perfeccionamiento y profundización de la dirección del Proceso de Enseñanza-Aprendizaje, este es un elemento que constituye una debilidad en la población diagnosticada.
En el caso de los estudiantes se seleccionó una muestra aleatoria simple de 168 estudiantes, de una población de 280. Se utilizó un error del 5 % y una confiabilidad del 95 %. La expresión utilizada para el cálculo del tamaño de la muestra es:
Donde:
n: |
tamaño de muestra |
N: |
tamaño de la población: 280 (1- 100 %: confiabilidad: 95 %) |
Z á/2: |
valor de la normal para una confiabilidad dada: 1.96 |
P: |
proporción esperada del porcentaje a medir: 0.5 e: error: 5% |
Se observaron 14 consultas, pertenecientes al tema cálculo diferencial y cuatro actividades metodológicas en los CUM y se revisó la preparación de la asignatura Matemática Superior I en cada centro universitario, previo al desarrollo del Proceso de Enseñanza-Aprendizaje del tema en el que se observaron las consultas.
La entrevista se aplicó individualmente a los directores de los centros universitarios municipales y jefes de departamento, y a los responsables de la asignatura Matemática en los Centros Universitarios Municipales. El 100 % son Licenciados en Educación y tienen más de 20 años de experiencia docente.
Se aplicaron dos encuestas, una de ellas al 100 % de los docentes. De ellos, cinco son licenciados en Educación en la especialidad de Matemática (62.5%) y tres son graduados universitarios de otras especialidades como ingeniería (37.5 %). La otra encuesta se aplicó a la muestra aleatoria de 168 estudiantes, representativa de la población de estudiantes de primer año de la carrera Contabilidad y Finanzas en la modalidad a distancia de la Universidad de Matanzas.
En el análisis de documentos se tomaron en consideración los siguientes: currículo base, Plan de estudio E carrera Contabilidad y Finanzas para curso semipresencial, Programa de Estudio de la Matemática Superior I, plan E para curso por encuentro, planes de clases (correspondientes a cada uno de los docentes que dieron consultas en primer año de la carrera Contabilidad y Finanzas), Resolución 47/2022, particularizando en lo relacionado con la semipresencialidad y la modalidad de educación a distancia.
Como prueba pedagógica se consideraron las preguntas sobre aplicaciones del cálculo diferencial a la economía de los exámenes finales de segundo año de Contabilidad y Finanzas, en que se hizo el diagnóstico
En el procesamiento estadístico se calculó la mediana de los datos obtenidos con los instrumentos aplicados. En el caso de la encuesta a los estudiantes se aplicó la prueba estadística de Kolmogorov-Smirnov, de bondad de ajuste, con un nivel de significación del 1 %, lo que permitió la determinación de tendencias en las opiniones de los estudiantes.
Resultados
Se constató, a través de la revisión de los documentos metodológicos y de organización de la carrera, la observación a actividades docentes, entrevistas y encuestas a docentes, estudiantes, egresados, jefes de departamento de diferentes CES del país, entre otros, que existen dificultades en la implementación del plan de estudio E con énfasis en la semipresencialidad. Se revelan vacíos teóricos en el trabajo didáctico, metodológico y teórico, que afectan la autogestión del aprendizaje en el Proceso de Enseñanza-Aprendizaje de la carrera, con énfasis en la disciplina Matemática: dificultades en el aprendizaje de los contenidos de la asignatura Matemática Superior I, a partir de las insuficiencias con los conocimientos básicos de niveles precedentes; débil desarrollo de habilidades en el uso de la tecnología para enfrentar los contenidos de la asignatura Matemática Superior I; limitada integración de los contenidos de la asignatura Matemática Superior I, a partir de un estudio fragmentado de la misma; pocas habilidades cognoscitivas para el trabajo con los medios y materiales docentes que permitan la autogestión del aprendizaje; existencia de dificultades para planificar y organizar el Proceso de Enseñanza-Aprendizaje en esta modalidad de estudio para la disciplina Matemática, en lo que la selección de métodos de enseñanza, medios y formas de organización para lograr el aprendizaje de la Matemática Superior I no siempre está en correspondencia con la modalidad a distancia; presentación de tareas matemáticas descontextualizadas en las guías de estudio, que no resultan motivantes ni significativas para los estudiantes; la solución de tareas complejas la realiza el docente, en la guía o en las actividades de consulta, sin detenerse a estimular a los estudiantes para su realización de manera independiente; el control y evaluación es casi nulo, se observó muy limitado en todo el proceso, por lo que los niveles de ayuda son escasos y en ocasiones conducen al fracaso; dificultades en la elaboración de los materiales de apoyo que permitan mayor autonomía y autogestión del aprendizaje por parte de los estudiantes; dispersión de la literatura, con un limitado acceso a las esencialidades de los contenidos.
A partir de la situación descrita, y al tratar la realidad vinculada a la necesidad de afianzar la autogestión del aprendizaje para poder aspirar a un desempeño profesional de calidad, se demuestra una contradicción científica entre lo que aspira la Educación Superior con el mayor acceso, ingreso y egreso de la población con la preparación necesaria para su desempeño exitoso como profesionales y el limitado proceder didáctico-metodológico para la autogestión del aprendizaje en el Proceso de Enseñanza-Aprendizaje de la Matemática Superior en condiciones de semipresencialidad, que contribuya a la formación de los profesionales de la carrera Contabilidad y Finanzas en la Universidad de Matanzas. Para la caracterización de la autogestión del aprendizaje en el Proceso de Enseñanza-Aprendizaje de la asignatura Matemática Superior I en Contabilidad y Finanzas en la semipresencialidad, primer año de formación, se partió del análisis del Modelo del Profesional y los programas para la formación. Para ello se realizaron las siguientes acciones: operacionalización de la variable, selección de la muestra, aplicación de métodos empíricos, análisis de las dimensiones y los indicadores, y valoración final sobre el estado actual de la variable.
De la sistematización realizada del objeto de estudio y del campo de acción, resultó la definición de la variable de investigación y la operacionalización de la variable en dimensiones e indicadores.
Para la variable de estudio se identificaron tres dimensiones: acciones del docente como tutor, desempeño de los estudiantes y resultados del aprendizaje. A continuación, se exponen los indicadores determinados para cada una de las dimensiones.
Dimensión 1. Acciones del docente como tutor.
1.1. Estado de la estructuración de los componentes didácticos.
1.2. Calidad de las tareas.
1.3. Pertinencia de su proceder didáctico para promover un aprendizaje desarrollador.
1.4. Eficacia en la configuración de relaciones estudiante-docente para propiciar el "aprender a aprender" Matemática, mediante la autogestión del aprendizaje.
Dimensión 2. Desempeño de los estudiantes.
2.1. Nivel de motivación por aprender el cálculo diferencial.
2.2. Modo de apropiación (activa, reflexiva y regulada).
2.3. Nivel de autogestión del aprendizaje.
Dimensión 3. Resultados del aprendizaje.
3.1. Nivel de asimilación del sistema de conocimientos y habilidades relativos al cálculo diferencial.
3.2. Nivel de logro alcanzado en la resolución de problemas económicos que requieren del cálculo diferencial.
3.3. Nivel de desarrollo adquirido en la autogestión del aprendizaje a lo largo de todo el Proceso de Enseñanza-Aprendizaje.
3.4. Nivel de relación comunicativa estudiante-docente.
Análisis del estado de las dimensiones y los indicadores
Para evaluar integralmente los indicadores se calculó la moda de los resultados obtenidos en la evaluación de estos, por cada uno de los instrumentos aplicados. Esto fue posible a partir de establecer una equivalencia entre las escalas empleadas en los instrumentos y las escalas determinadas para evaluar los indicadores
Dimensión 1. Acciones del docente como tutor.
1.1. El estado de la estructuración de los componentes didácticos en el Proceso de Enseñanza-Aprendizaje de la Matemática Superior I, para que los estudiantes realicen la autogestión del aprendizaje, fue evaluado de poco adecuado, lo que se evidencia en que a veces los docentes estructuran en sus consultas los componentes didácticos, de manera que los estudiantes realicen la autogestión del aprendizaje matemático, a partir de las orientaciones para que puedan resolver problemas económicos. En las actividades metodológicas es insuficiente el tratamiento que se le da a la estructuración de los componentes didácticos, en función de que los estudiantes realicen la autogestión del aprendizaje.
En las consultas observadas y sus planes revisados se pusieron de manifiesto insuficiencias en: el dominio de los componentes didácticos por los docentes y la poca correspondencia del estudio individual orientado con los objetivos del programa y los niveles de asimilación; en la selección y aplicación de los métodos, en función de lograr mayor motivación de los estudiantes y la búsqueda reflexiva, valorativa e independiente del conocimiento y el cumplimiento de los objetivos; en las tareas, en función de los intereses de los estudiantes y de situaciones prácticas de su entorno profesional, que contribuyan al desarrollo de la autogestión del aprendizaje de los contenidos matemáticos. En la orientación del estudio independiente se plantean tareas poco exigentes donde, por ejemplo, no se potencian problemas económicos donde se obtengan los resultados por los propios estudiantes.
El programa de la asignatura no responde al curso a distancia sino al curso por encuentro, porque los componentes didácticos no están dirigidos a la esencialidad de los contenidos. La ubicación de los contenidos y la cantidad de horas/consultas asignadas es insuficiente, lo que no favorece el desarrollo de la asimilación de los contenidos.
En la resolución 47/2022, artículo 19, se recoge como exigencia el aprendizaje autónomo, apoyado en el empleo de diferentes recursos educativos que permitan la adaptabilidad a las necesidades cognitivas y ritmo de aprendizaje de los estudiantes, así como la comunicación multidireccional entre los diferentes actores del proceso de formación, donde es fundamental la labor tutorial; para ello son insuficientes los materiales elaborados por los docentes. En los libros: Matemáticas para el Análisis Económico I y II (Sydsaeter, Hammonnd, 2003) y Laboratorio Matemática I Y II (Marrero et al., 2010), los contenidos no están enfocados hacia una mejor comprensión, pues en ocasiones se omiten pasos de los algoritmos suponiendo que los estudiantes lo dominan, lo que no favorece la autogestión del aprendizaje y con ello la motivación hacia el "aprender a aprender" Matemática para solucionar problemas de la profesión.
1.2. La calidad de las tareas para la realización de la autogestión del aprendizaje matemático fue evaluada de poco adecuada, lo que se manifiesta en que:
Casi nunca se relacionan con el contexto; aun cuando en algunas ocasiones se refieren de manera general a la práctica social, no se tiene en cuenta el contexto específico de la profesión. Son poco variadas y no exigen niveles crecientes de asimilación, pues se limitan a la resolución de problemas matemáticos sin vinculación a la economía.
No siempre promueve la búsqueda de información en diferentes fuentes y medios.
Rara vez se exige el establecimiento de relaciones interdisciplinarias con las otras asignaturas del currículo y la realización del trabajo colectivo con implicaciones individuales.
1.3. La pertinencia de su proceder didáctico para promover un aprendizaje desarrollador fue evaluada de poco adecuada, manifestado en que:
Casi nunca los docentes logran, con su proceder didáctico, que los estudiantes puedan realizar la autogestión del contenido matemático, a partir de que no consideran las posibilidades y diferencias individuales de los estudiantes, ni combinan el trabajo individual y colectivo utilizando diferentes formas de organización; los métodos y procedimientos no orientan al estudiante hacia la búsqueda, independiente del conocimiento en diversas fuentes y medios.
Es débil la orientación hacia los objetivos, debido a que son escasas las actividades dirigidas a que el estudiante reconozca el objetivo de la consulta y los pasos necesarios para alcanzarlo, mediante la realización de acciones que propicien la reflexión y valoración del contenido.
Generalmente no se aplican estrategias de aprendizaje que favorezcan la asimilación y fijación de la nueva materia.
El control que se ejerce del aprendizaje de los estudiantes carece de sistematicidad y no siempre tiene como objetivo comprobar los resultados de la autogestión del aprendizaje.
Los programas de estudio van dirigidos hacia la modalidad semipresencial, en curso por encuentro, por lo que carecen de la esencialidad de los contenidos para la modalidad que se estudia, lo que afecta el proceder didáctico de los docentes para el buen desarrollo del Proceso de Enseñanza-Aprendizaje a distancia.
En las actividades metodológicas es insuficiente el trabajo con los docentes para que se preparen para promover estrategias de aprendizaje y de trabajo individual propios para la autogestión del aprendizaje. No se ofrecen orientaciones para diagnosticar las potencialidades y dificultades en contenidos relacionados con la profesión, ni se proyecta cómo darle tratamiento.
En las consultas observadas y los planes revisados se puso de manifiesto que los contenidos nuevos se relacionan con los anteriores, pero muy poco con la vida cotidiana y la profesión. Son escasas las acciones encaminadas a preparar a los estudiantes para realizar la autogestión del aprendizaje de los contenidos matemáticos, porque las tareas no contemplan acciones para realizar estrategias de aprendizaje. El trabajo del docente hacia la motivación por el aprendizaje no se hace a partir de tareas con contenidos de la vida cotidiana y de la profesión.
1.4. La eficacia en la configuración de relaciones estudiante-docente para propiciar el "aprender a aprender" Matemática, mediante la comunicación, fue evaluada de poco adecuada, evidenciado en que a veces se estimula desde la consulta la utilización de métodos y procedimientos por los estudiantes; que estos contribuyan a su desarrollo, en particular, para organizar, planificar, controlar y evaluar su trabajo, que estimulen la confianza en las propias capacidades, el establecimiento de metas, la reflexión, la aplicación de estrategias para aprender, la valoración positiva del error, el trabajo cooperativo y el desarrollo de actitudes positivas. Son insuficientes las acciones para orientar a los docentes en acciones para lograr una comunicación pertinente entre los protagonistas del proceso. En las consultas observadas y sus planes revisados se puso de manifiesto que no se promueven estrategias de aprendizaje y de trabajo mental propios de la asignatura Matemática.
En la dimensión "Acciones del docente como tutor" se pueden señalar de forma general las siguientes dificultades: la estructuración de los componentes didácticos, en ocasiones, no es adecuada; las tareas resultan de poco interés para los estudiantes, pues en su mayoría no están vinculadas a la profesión y el proceder didáctico del docente y las relaciones docente-estudiante no propician que puedan realizar la autogestión del aprendizaje, ni el "aprender a aprender" Matemática. Entre las potencialidades de la dimensión se puede plantear la disposición de los docentes para superarse en los contenidos relacionados con las aplicaciones del cálculo diferencial en los problemas económicos y su didáctica.
Dimensión 2. Desempeño de los estudiantes.
2.1. El nivel de motivación intrínseca por aprender contenidos de Matemática es medianamente adecuado, lo que se manifiesta en que:
A veces se logra la motivación intrínseca por aprender y la consiguiente comprensión del papel de la Matemática en la economía y, a su vez, en la sociedad, en el Proceso de Enseñanza-Aprendizaje.
El trabajo del docente hacia la motivación por el aprendizaje carece de tareas relacionadas con las aplicaciones del cálculo diferencial en los problemas económicos y de interés para los estudiantes.
Es insuficiente la selección y aplicación de los métodos, en función de lograr mayor motivación de los estudiantes y la búsqueda reflexiva, valorativa e independiente del conocimiento y el cumplimiento de los objetivos.
Son insuficientes las tareas en función de los intereses de los estudiantes y de situaciones prácticas de su entorno profesional, que contribuyan al desarrollo de habilidades y su autonomía. Falta de interés para realizar actividades de aprendizaje e intercambios con sus compañeros en el grupo.
2.2. El modo de apropiación (activa, reflexiva y regulada) de los contenidos matemáticos fue evaluado de poco adecuado, evidenciado en que:
Casi nunca o nunca resuelven los problemas mediante la utilización de diferentes vías de solución y es limitada la reflexión sobre la vía utilizada en la resolución de estos.
El 75 % de los docentes y el 56,8 % de los estudiantes consideran que casi nunca logran la apropiación de manera activa, reflexiva y regulada de los contenidos matemáticos, lo que justifica que los estudiantes no demuestren habilidades para analizar problemas económicos de la profesión, pues la mayoría de las veces solo llegan a plantear lo dado y lo que se busca sin llegar a encontrar la vía de solución.
Generalmente, muestran poca independencia, flexibilidad, racionalidad y originalidad en los procesos de pensamiento y en la resolución de problemas.
2.3. El nivel de autogestión del aprendizaje fue evaluado de poco adecuado, manifestado en que:
Casi nunca se logra la autogestión del aprendizaje de los contenidos matemáticos. El 75 % de los docentes considera que los estudiantes no poseen las tecnologías, en su sentido amplio de la palabra, para trabajar de manera independiente, sin presencia del docente. Casi nunca aplican los conocimientos anteriores en la resolución de los problemas económicos de la profesión, lo que incide en que la tendencia en los estudiantes es a no lograr autogestionarse el aprendizaje. Resuelven muy pocos problemas relacionados con su contexto profesional y casi nunca relacionados con sus intereses personales.
Escasamente los estudiantes realizan de forma independiente diferentes tipos de tareas en las que integren los contenidos, que respondan a distintos niveles de asimilación y que requieran la búsqueda de contenidos precedentes.
En el 67 % de las consultas observadas se evidenció que no se favorece un clima psicológico hacia el aprendizaje autónomo, dando la posibilidad a los estudiantes de expresar sus opiniones y juicios para contribuir al desarrollo de su modo de actuación y no se logra la motivación y disposición hacia la autonomía.
En los planes de consultas es casi nula la orientación hacia los objetivos mediante acciones reflexivas y valorativas de los estudiantes, teniendo en cuenta para qué, qué, cómo y en qué condiciones van a aprender.
En la dimensión "Desempeño de los estudiantes", se pueden señalar de forma general las siguientes dificultades: no se propicia de manera suficiente que los estudiantes se impliquen de forma autónoma e independiente en el contenido matemático y en la búsqueda del conocimiento necesario y no siempre se establecen relaciones necesarias entre los contenidos, ni se distinguen por los estudiantes las diferentes maneras de obtener los conceptos y definiciones matemáticas. Entre las potencialidades de la dimensión se puede plantear que los estudiantes no hacen rechazo a la Matemática Superior I.
Dimensión 3. Resultados del aprendizaje de los estudiantes.
3.1. El nivel de asimilación del sistema de conocimientos y habilidades relativos a la Matemática Superior I fue evaluado de poco adecuado, lo que se evidencia en la opinión de los docentes; casi nunca los estudiantes demuestran en los distintos tipos de tareas los conocimientos y habilidades de la Matemática, lo que no les permite integrar y sistematizar los contenidos para resolver problemas económicos de la profesión.
La tendencia en la opinión de los estudiantes es que casi nunca logran la asimilación del sistema de conocimientos y habilidades relativas a la Matemática Superior I.
Son insuficientes las acciones que desarrolla el docente en las consultas para controlar y evaluar el aprendizaje y les dan pocas posibilidades a los estudiantes para que puedan demostrar la asimilación del contenido.
En la prueba pedagógica no se alcanzan buenos resultados, el contenido evaluado no es simple y en el mismo se consideran habilidades precedentes para analizar problemas económicos de la profesión, aplicando el cálculo diferencial.
3.2. El nivel de logro alcanzado en la resolución de problemas económicos de la profesión, que requieren del cálculo diferencial, fue evaluado de inadecuado, lo que se evidencia en que rara vez los estudiantes desarrollan adecuadamente las tareas donde deben desarrollar las habilidades relacionadas con el cálculo diferencial, según la opinión de los docentes.
La tendencia es que casi nunca tienen logros en la resolución de tareas que requieren del cálculo diferencial, lo que se manifiesta en que no tienen habilidades, ni el nivel de desarrollo de su razonamiento lógico y cualidades de la personalidad para realizar de manera integral el análisis del problema.
En las observaciones a consultas se observó que en el 58 % de estas se desarrollan muy pocas tareas que promuevan, en su realización, que los estudiantes valoren los resultados obtenidos y arriben a conclusiones.
3.3. El nivel de desarrollo adquirido en la autogestión del aprendizaje a lo largo de todo el Proceso de Enseñanza-Aprendizaje fue evaluado de inadecuado, manifestado en que, de la encuesta a docentes se obtuvo que el 88 % de estos reconocen que en la resolución de las tareas los estudiantes no lleguen a la solución de los problemas utilizando adecuadamente los conceptos, la terminología y simbología de la matemática y del cálculo diferencial en particular. La tendencia en la opinión de los estudiantes es que casi nunca logran la solución de tareas, no son capaces de realizar correctamente los problemas utilizando los conceptos, la terminología y simbología de la matemática y del cálculo diferencial en particular.
De la observación a consultas se constató que en estas no se logra que los estudiantes expliquen las tareas con los conceptos, la terminología y simbología de la matemática, y del cálculo diferencial en particular, en la resolución de problemas económicos de la profesión.
3.4. El nivel de manifestación de cualidades positivas en los estudiantes y el grupo fue evaluado de poco adecuado, lo que se aprecia en que no siempre manifiestan actitudes positivas y valores durante el Proceso de Enseñanza-Aprendizaje; apenas demuestran sus cualidades positivas y las del grupo, lo que coincide con la opinión de los docentes y se justifica en que casi nunca son capaces de identificar, valorar y superar los errores cometidos y mostrarlo en el trabajo del grupo. No exponen en los distintas tareas, independencia y responsabilidad en su resolución ni ponen de manifiesto la perseverancia y el espíritu crítico; además, no siempre demuestran laboriosidad y responsabilidad a partir de las tareas que realizan y muestran respeto por los juicios y resultados obtenidos por sus compañeros. En la observación a consultas se constataron las insuficientes acciones que desarrollan los docentes para orientar hacia la autonomía, la independencia, la responsabilidad, perseverancia y la creatividad.
En la dimensión "Resultados del aprendizaje de los estudiantes", se constata que los estudiantes alcanzan un dominio mínimo de los contenidos de la Matemática, presentan dificultades en la interpretación y resolución de problemas económicos y no pueden poner sus conocimientos y habilidades en acción en la resolución de problemas que exigen la utilización del cálculo diferencial.
Discusión
El análisis de la literatura consultada permitió precisar que autores como Faustino et al. (2019); González et al. (2018); Radovic, Black, Williams & Salas (2018), Naveira & Valdivia (2022), entre otros, aportan elementos fundamentales para el Proceso de Enseñanza-Aprendizaje de la Matemática, pero no particularizan para la Educación Superior en la modalidad a distancia y solo estudian algunas situaciones o casos en particular, por lo que se necesita un actuar profundo que permita estructurar las orientaciones de todos los contenidos de la disciplina Matemática Superior para las diferentes carreras universitarias, en esta modalidad de estudio. De la misma manera, se concuerda con lo expresado con Bonet et al. (2018); Leyva & Lariot (2019); Zae et al. (2020); Metaute et al. (2020), quienes definen y caracterizan la autogestión del aprendizaje, lo que no es abordado para la enseñanza de la Matemática, pero se concuerda en que la autogestión del aprendizaje es individual, depende de los retos y aspiraciones de las personas, así como de su responsabilidad ante las tareas que debe desarrollar. Los autores del presente artículo añaden que es necesaria la preparación del docente y del estudiante para enfrentar los retos en esta modalidad de estudio en la que aparece, además, con mayor fuerza, la utilización de las TIC como mediadores, de acuerdo a su desarrollo en la sociedad del conocimiento, para facilitar la autogestión del aprendizaje en el Proceso de Enseñanza-Aprendizaje desarrollador de la Matemática Superior I.
Lo anterior permite definir la autogestión del aprendizaje en el Proceso de Enseñanza-Aprendizaje en la asignatura Matemática Superior I de la carrera Contabilidad y Finanzas en condiciones de semipresencialidad, como un proceso integral, planificado, organizado y correctamente orientado, esencialmente asincrónico, con el empleo de las Tecnologías de la Información y las Comunicaciones, que favorezca la participación activa del estudiante en el Proceso de Enseñanza-Aprendizaje. Para ello supone un alto grado de interés, compromiso y responsabilidad que le permiten responder a las exigencias del desarrollo de las habilidades del cálculo diferencial para resolver los problemas profesionales del contador. La definición anterior apunta a la necesaria preparación de los actores del proceso para enfrentarlo con éxito y se precisa que debe estar en correspondencia con los modos de actuación del futuro profesional y responder a las exigencias de la sociedad.
Los resultados obtenidos en el proceso de diagnóstico sobre el estado actual de la variable de la investigación permitieron concluir que el Proceso de Enseñanza-Aprendizaje de la Matemática Superior I en la modalidad a distancia, en los estudiantes de primer año de la carrera Contabilidad y Finanzas, está caracterizado por insuficiencias en la dirección del Proceso de Enseñanza-Aprendizaje hacia la independencia y autogestión del aprendizaje, condicionadas por dificultades en la estructuración de los componentes didácticos para que los estudiantes puedan alcanzar la autonomía y así lograr resolver problemas económicos a través del cálculo diferencial; así como en la preparación metodológica y el dominio de la esencialidad del sistema de conocimientos de la Matemática Superior I por parte de los docentes, para planificar, organizar, ejecutar y controlar/evaluar el Proceso de Enseñanza-Aprendizaje de la Matemática Superior I.
El aprendizaje de los estudiantes, comprobado a través de los resultados de las evaluaciones que se aplican, no es favorable, con la mirada hacia el proceso. Presenta deficiencias en cuanto a la autogestión del aprendizaje, la búsqueda del contenido precedente y siguiente, que debe saber para resolver problemas económicos a través del cálculo diferencial, el arribo a la solución y la interpretación económica del resultado, así como con las habilidades, procesos de pensamiento y cualidades de la personalidad requeridas para con la Matemática.
Los resultados obtenidos permiten valorar la necesidad de buscar alternativas que mejoren la situación diagnosticada.











 texto en
texto en