Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Para trabajar indicadores demográficos es necesario tener datos de la población objeto de estudio. Con esos datos se calculan los indicadores que son interés del investigador y con ello se interpreta el fenómeno y en la mayoría de los casos esos resultados son insumos para la elaboración e implementación de políticas públicas. De ahí la importancia de que los datos utilizados sean confiables y los resultados robustos, pues de ello depende la eficiencia de la política. Una mala lectura de un dato podría tener consecuencias negativas en un territorio, pues al no reflejar la realidad, no estaría realmente resolviendo las problemáticas y probablemente estaría creando otras.
En el caso de áreas pequeñas, con poblaciones pequeñas, muchas veces sucede que los indicadores muestran resultados que no se corresponden con la tendencia normal del indicador. Esto gravita en que las lecturas y las interpretaciones no tengan sustento y no se puedan trabajar de manera correcta. Asimismo los eventos ocurridos podrían ser raros y aleatorios, lo cual lleva a que no reflejen la realidad en el territorio.
Por esta razón es necesario tomar mucho cuidado cuando se trabaja en áreas pequeñas, pues la mayoría de las veces área pequeña es sinónimo de población pequeña. El presente trabajo explica brevemente por qué no es posible trabajar en áreas pequeñas con el cálculo directo de los indicadores. Asimismo se define cuándo podemos considerar a una población como pequeña y se brindan dos formas alternativas de trabajar con datos de esas poblaciones, para obtener resultados más robustos y corregidos y que se acerquen a la realidad de los territorios. El primer método es el cálculo del indicador para un período de tiempo, ya sea trianual o quinquenal, lo cual aumenta el número de eventos y de personas en esa población. El segundo se refiere a la tipificación indirecta, en el que se utiliza una población patrón donde los números sean mayores y se le aplica a la población en cuestión.
De esta manera, en el presente texto se pretende alertar sobre el hecho de que en áreas pequeñas con poblaciones pequeñas es imprescindible considerar que los resultados de indicadores calculados de la manera tradicional no pueden ser utilizados en la interpretación de los fenómenos. Por otro lado se ofrecen herramientas sencillas que permiten el cálculo, les dan mayor robustez y confiabilidad a los resultados y, por tanto, hacen que estos reflejen con mayor claridad la realidad.
Los datos en áreas pequeñas
En respuesta a la pregunta de por qué debemos tener cuidado cuando trabajamos con datos de población en áreas pequeñas, se podría decir que, en primer lugar, por lo general cuando se trabaja en áreas pequeñas se está trabajando con poblaciones pequeñas. Es por esa razón que en este caso no se podría trabajar simplemente con el número de eventos y la población observada en el período deseado, especialmente si se trata de un año. A esto se le suma que cuando se estratifica la información o se quieren trabajar diferenciales de determinada variable, el problema es aún mayor, pues tanto la población objeto de estudio como los eventos disminuyen aún más en número.
Un área es considerada como pequeña cuando el tamaño de la muestra no permite realizar estimaciones directas para obtener resultados robustos y confiables. Aunque por lo general sucede, tener muestras pequeñas no siempre se relaciona con fuentes de información que se refieren a áreas pequeñas, muchas veces existen fuentes de grandes áreas que no permiten realizar estimaciones confiables para determinadas características o determinados grupos. Siendo así, se puede presentar el problema tanto para un área pequeña como para una población pequeña o la combinación de ambas. Por lo general cuando trabajamos en pequeñas áreas estamos ante poblaciones pequeñas.
En este escenario se combina una cuota baja de población con eventos demográficos raros, donde la incidencia de los eventos genera fluctuaciones aleatorias en los indicadores calculados. Por otro lado el número de eventos no necesariamente muestra la dinámica real, por ejemplo, en el caso de la mortalidad podría ser que en un período en determinado grupo etario no hubo defunciones, lo cual genera que el indicador de mortalidad tiene automáticamente un valor 0. Esto significa que la probabilidad de muerte se convierte en 0 y se interpreta como que no hay probabilidad de muerte en esa edad durante ese período y en esa área, lo cual se sabe que es imposible, pues una de las características de la mortalidad es que la población está expuesta al riesgo de morir durante toda la vida.
Una de las cosas más debatidas es justamente el hecho que cómo definir cuando estamos frente a una población pequeña, donde no es viable hacer estimaciones directas. En este sentido Assunção, Potter y Cavenaghi (1998), definen una población pequeña cuando se refiere a un área geográfica donde la variabilidad de las estimaciones a partir de los datos de esta zona produce desviaciones estándares inaceptables debido a su enorme tamaño. Esta es la consecuencia de que exista un pequeño número de personas en situación de riesgo, además de que por lo general los eventos del fenómeno en estudio son raros. Así, con la misma base de datos, un área se puede considerar pequeña en algunos casos y en otros no.
Desde esta perspectiva es importante aclarar que no necesariamente existe un número mágico de población o de eventos que nos permita definir si estamos ante poblaciones pequeñas. Obviamente existen casos en los que es evidente que estamos en presencia de una población pequeña (se podría pensar en el ejemplo donde no se observan muertes); sin embargo, muchas veces podemos pensar que tenemos un número de eventos que permite analizar tendencias, pero al observar los resultados se perciben fluctuaciones que muestran que estamos ante una población pequeña. Con esta lógica, se podría identificar que estamos trabajando con una población pequeña cuando las fluctuaciones observadas en los indicadores son aleatorias. En la definición de Assunção, Potter y Cavenaghi (1998) se utiliza el término área pequeña, sin embargo, a lo largo del presente trabajo se utilizará el término población pequeña, pues en la práctica se trabaja con población. Efectivamente, un área pequeña genera que se esté ante poblaciones pequeñas en la mayoría de los casos, no obstante, en no pocas ocasiones el hecho de trabajar con muestras o con grupos que son de interés del investigador reducen el número de individuos de forma que, a pesar de estar trabajando con un área grande y un gran universo de personas, nuestra muestra se convierte en pequeña. Es por ello que el hecho de considerar una población como pequeña no depende de la cantidad de personas de la muestra o el tamaño del área a la que pertenezca esa muestra, sino por el comportamiento de los indicadores calculados con esos datos como base.
Naciones Unidas considera para realizar sus proyecciones de población solo países con más de 90 000 habitantes (Castanheira, Pelletier y Ribeiro, 2017). Lugares con poblaciones por debajo de esta cifra son consideradas como pequeñas y por tanto no se proyectan. Por otro lado autores como Freire y Assunçao han desarrollado trabajos aplicando diferentes métodos para estimar indicadores demográficos en pequeñas áreas. En muchos contextos es necesario e imprescindible tener información sobre la dinámica demográfica, especialmente para la planificación a nivel local y para elaborar e implementar políticas públicas. Es por ello que a pesar de los errores que pudieran generar los métodos y los supuestos realizados para la estimación, es importante buscar soluciones y obtener resultados que permitan brindar insumos en los territorios donde las estimaciones no pueden ser realizadas directamente por el pequeño número de personas y de eventos.
En el presente trabajo se muestran ejemplos de cómo identificar cuando estamos en presencia de una población pequeña. Asimismo se muestra el método de tipificación indirecta para realizar estimaciones en pequeñas áreas donde tanto el número de eventos como la cantidad de población no permiten realizar análisis a partir de estimaciones directas.
Pequeñas áreas y poblaciones pequeñas
Como ya se ha mencionado, usualmente cuando trabajamos en un área pequeña, nos enfrentamos también a una población pequeña. Sin embargo, no siempre que estamos ante una población pequeña es producto de que trabajamos en pequeñas áreas. En ocasiones es justo el tamaño de la muestra y la población objeto de estudio la que define resultados típicos de una población pequeña.
Un área geográfica se podría identificar como área pequeña cuando la variabilidad de las estimaciones a partir de los datos observados en esta zona produce desviaciones estándar inaceptables debido a su enorme tamaño. Esto es producto del pequeño número de personas en situación de riesgo, relacionado con la rareza de los eventos del fenómeno en estudio. Así, con la misma base de datos, un área se puede considerar pequeña en algunos casos y en otros no (Assunção, Potter y Cavenaghi, 1998). Aunque por lo general sucede, tener muestras pequeñas no siempre se relaciona con fuentes de información que se refieren a áreas pequeñas, muchas veces existen fuentes de grandes áreas que no permiten realizar estimaciones confiables para determinadas características o determinados grupos.
Matemáticamente, cuanto menor es el número de observaciones, menos robustos son los resultados y menos se acerca el resultado a la probabilidad real de que ocurra un fenómeno. Por ejemplo, en una población de 10 personas mueren 2 y la tasa observada sería 0,2. Al año siguiente en esa misma población de 10 personas hay una muerte más, es decir, 3 muertes en total y la tasa observada aumenta 0.3. En el grupo estudiado la tasa de mortalidad aumentó un 50% de un año a otro sin que pudiera darse una explicación al fenómeno pues las condiciones fueron las mismas.
Por otro lado tenemos una población de 100 personas donde un año mueren 20 personas y al año siguiente mueren 21. De esta manera las tasas serían 0.2 y 0.21 respectivamente y el aumento de un año a otro sería de un 5%. Por último tenemos una población de 1 000 personas con la misma dinámica de mortalidad que las poblaciones anteriores, donde la diferencia entre el número de muertes entre un año y otro es 1, y el primer año mueren 200 personas y al año siguiente mueren 201. De esta manera las tasas observadas serían 0.2 y 0.201 respectivamente con un aumento de un año a otro del 0.5%.
Estos ejemplos muestran cómo el tamaño de una población influye en que se obtengan resultados robustos y fidedignos, que permitan realizar interpretaciones acertadas de la realidad. Los ejemplos mostraron cómo un igual aumento en el número de muertes en iguales condiciones genera desviaciones muy diferentes, disminuyendo las diferencias cuando aumenta el número de población.
A continuación se muestran dos poblaciones reales, al área menor le llamaremos municipio A y al área mayor provincia A. La figura 1 muestra el comportamiento de la tasa específica de mortalidad en las dos poblaciones en estudio para el año 2010.
Nótese que en área menor A, la mortalidad por edades no sigue el patrón normal de las tasas específicas de mortalidad, en el que en las primeras edades la mortalidad es alta, luego decrece su valor y seguidamente sigue un crecimiento ininterrumpido y directamente proporcional con la edad. Asimismo en los primeros grupos de edades se muestran tasas 0 lo cual se pudiera interpretar como 0 mortalidad y por tanto no existe riesgo de muerte (considerando que la tasa específica de mortalidad se utiliza para calcular probabilidad de muerte en cada edad). Es obvio que este resultado no es real puesto que la mortalidad es un riesgo al que se está expuesto durante toda la vida (Welti, 1998) y es esta una de las características principales de esta variable.
Por otro lado la línea del área mayor (provincia A) se acerca más al patrón teórico en el que se describen dos curvas, una curva en forma de U y una en forma de J. la primera es característica de poblaciones con mortalidad infantil alta y la segunda muestra valores bajos en las primeras edades, por eso la forma de J, donde en los primeros grupos la mortalidad es menor que en las edades adultas por encima de los 45 años (Welti, 1998). Igualmente no se observan valores 0 en ningún grupo. Esto evidencia que el tamaño de la población en estudio define si estamos ante datos que pueden ser evaluados a partir de métodos directos de estimación o no.
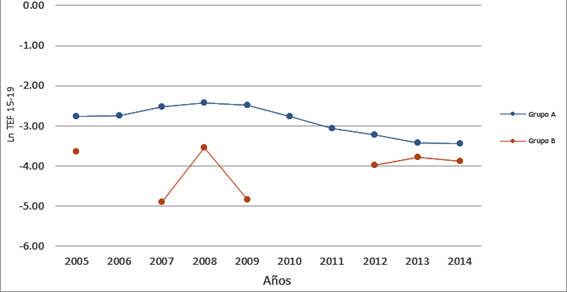
Un segundo ejemplo que puede resultar interesante es el de la evolución de la fecundidad adolescente en dos grupos de muchachas en un período de 10 años. El primer grupo es el resultado de una encuesta por muestreo y el número de observaciones es muy reducido y el segundo es el de la población femenina de un país (figura 2).
En el caso del grupo A (observación de un país completo) se puede definir una tendencia al descenso a partir del año 2008 aproximadamente, y en el 2013 hubo un ligero estancamiento en esa caída. A partir de este comportamiento se puede analizar la evolución de este indicador y a partir del contexto en el que se desarrolla elaborar hipótesis explicativas al fenómeno. En la línea del grupo B (resultado de una encuesta por muestreo y reducido a la muestra que nos interesa estudiar a partir de características que son del interés del investigador) no es posible realizar un análisis de la tendencia. Existe ausencia de datos en determinados años donde no se observa incidencia del evento, además de fluctuaciones que muestran un aumento entre el 2007 y el 2008, y una disminución entre este y el 2009 que no encuentra explicación en el contexto en el que se desarrolla.
En estos casos en los que es evidente que no se puede realizar un análisis a partir de los datos observados con cálculos directos, se hace necesario aplicar métodos de estimación indirecta que nos permitan estudiar el fenómeno.
La tipificación indirecta como método de estimación de indicadores en poblaciones pequeñas
La tipificación indirecta es un procedimiento utilizado para estimar indicadores demográficos en ausencia de las informaciones necesarias para calcularlos con los datos reales (Preston, Heuveline y Guillot, 2000). En el caso que nos ocupa (pequeñas áreas), aunque se tiene la información, esta no es fiable, pues los resultados alcanzados con ella no reflejan la realidad y por tanto no son robustos. Para realizar el ejercicio lo primero es escoger una población patrón de la cual tenemos todas las tasas específicas y que tenga características similares a la nuestra. Es muy importante escoger el patrón correctamente, pues al realizar el procedimiento asumimos que nuestra población tiene las mismas condiciones que la nuestra. Una vez escogido el patrón le aplicamos las tasas específicas a nuestra estructura etaria.
El ejemplo que utilizaremos en el presente trabajo será de la mortalidad de una población real a la que llamaremos región menor. No es posible realizar un análisis de la mortalidad en dicha región con los datos reales que se ofrecen, por tanto se realizarán las estimaciones a partir del método de tipificación indirecta. Para ello se escogerá como patrón una población igualmente real que será denominada región mayor como área mayor, pues el área menor muestra condiciones muy semejantes al área mayor.
Después de escoger el juego de tasas específicas de mortalidad del patrón (región mayor) y teniendo la estructura etaria de nuestra población objeto de estudio (región menor), el primer paso es el cálculo de las muertes esperadas. Este cálculo se realiza a partir del despeje de la fórmula tradicional para el cálculo de las tasas específicas de mortalidad:
Donde D son las defunciones y es la población media. Las tasas específicas las tenemos, pues es el patrón que será utilizado y como población se usa la estructura etaria de la población objeto de estudio. Por tanto habría entonces que estimar las muertes, que serían las muertes esperadas para el área menor si tuviera el régimen de mortalidad de la región mayor. Quedaría entonces de la siguiente manera:
Así, las defunciones que tendría el área menor serían el resultado de la tasa específica de mortalidad en cada grupo etario del patrón multiplicado por la estructura de la población con los datos observados en esta área (peso de cada grupo sobre la población total). Una vez calculadas las defunciones esperadas en cada grupo, estas se suman y se multiplican por 1000 (el resultado sería semejante a la tasa bruta de mortalidad) y de esta manera se tiene el total de defunciones esperadas para la región menor si tuviera las condiciones de mortalidad de la mayor. Al tener esta información es necesario entonces calcular un factor de corrección que ajusta nuestra curva de mortalidad en función de la estructura etaria observada, es decir, asumimos que la estructura de la mortalidad en el área menor sigue el mismo comportamiento de la región mayor; sin embargo, el nivel es diferente y es justamente esto lo que debemos corregir. Para ello el factor de corrección se calcula de la siguiente manera:
De esta manera estaríamos calculando el factor de corrección de la mortalidad (FCM) como el resultado de las defunciones esperadas dividido por las defunciones observadas. Donde las defunciones observadas serían la tasa bruta de mortalidad observada en la región menor, pues en el numerador la suma de las defunciones esperadas se multiplicó por 1000 y en ese caso estaríamos dándole el mismo tratamiento a las dos cifras.
Por último, este factor de corrección (que también se le puede denominar K) se le aplica a las tasas específicas del patrón y de esta manera se puede ajustar la estructura de la mortalidad en función de la estructura etaria del área menor que es nuestro objeto de estudio. Siendo así, el último paso sería:
Siendo que las tasas específicas tipificadas del municipio A serían el resultado de las tasas específicas del patrón por el factor de corrección.
Una vez explicado el método se hace necesario colocar el ejemplo con cifras para un mejor entendimiento del fenómeno. El objetivo del ejercicio es estimar la mortalidad en el área menor; sin embargo, es una población muy pequeña donde los eventos son raros, lo cual provoca fluctuaciones aleatorias en las tasas, incluso hay grupos de edades donde la mortalidad es 0, por tanto, aunque los datos existen, los resultados a partir de los datos observados no son confiables. Tenemos los siguientes datos (tabla 1):
Tabla 1 Defunciones, población media y tasas específicas de mortalidad de la región menor y la región mayor. 2010
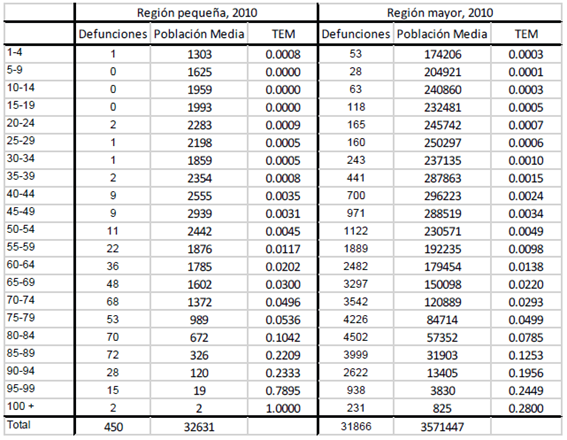
Fuente: Elaboración propia.
Como se observa en la tabla, las defunciones observadas en el área menor muestran pequeños números, incluso grupos de edades donde no hubo muertes ese año. Para confirmar que efectivamente el comportamiento de la mortalidad por edades en esta área pequeña necesita una estimación que permita interpretar el resultado correctamente, a continuación se muestra un gráfico con las tasas específicas de mortalidad para esta área. En la figura 3 se observa cómo el patrón de la mortalidad en esta área muestra vacíos en las edades desde los 5 hasta los 19 años, de lo cual podría interpretarse que en estas edades la mortalidad es nula en esta región, cosa que, como ya se explicó al principio del trabajo, no es posible. Asimismo existen fluctuaciones en otros grupos de edades que salen del patrón tradicional de la mortalidad por edades, como por ejemplo en las edades 45-49 y 90-94, donde la mortalidad es menor que en el grupo anterior respectivamente, siendo que en edades avanzadas la mortalidad aumenta con la edad. Siendo así, es evidente que sería necesario aplicar algún método de estimación indirecta para analizar la mortalidad.
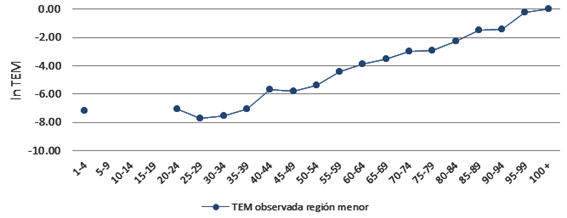Fuente: Elaboración propia.Figura 3 Tasas específicas de mortalidad observadas de la región menor. 2010
Al utilizar la tipificación indirecta necesitamos escoger un patrón para trabajar con las tasas específicas de mortalidad, y para ello los datos disponibles pertenecen a la región mayor que muestra condiciones semejantes al área menor en estudio. Con los datos de la tabla 1 se calculan las defunciones esperadas y el factor de corrección para estimar las tasas específicas de mortalidad para la región menor. La tabla 2 muestra los resultados del procedimiento con el cálculo de las defunciones esperadas, el factor de corrección y las tasas específicas de la región pequeña tipificadas.
Tabla 2 Ejercicio de tipificación indirecta para estimar las tasas específicas de mortalidad de la región menor
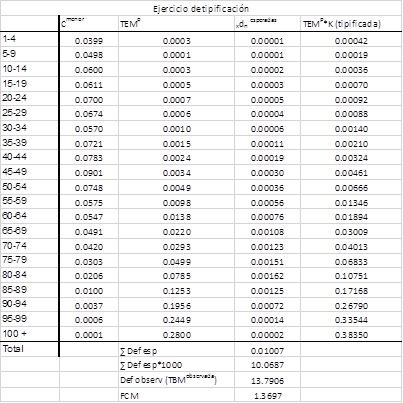
Fuente: Elaboración propia.
El número de defunciones esperadas si la población menor tuviera la misma estructura de la mortalidad que el área mayor es menor que el número real observado en el área menor. Esto se expresa además en el factor de corrección que es mayor que 1, lo cual indica que el patrón muestra un nivel de la mortalidad menor que el área menor que se está tipificando. Al aplicar el factor de corrección para ajustar las tasas específicas del patrón se obtienen nuestras tasas específicas tipificadas para la región menor, que sería el objetivo del ejercicio. La figura 4 muestra cómo se ha corregido la curva de mortalidad por edades en la población pequeña luego de la tipificación y se compara además con la estructura patrón.
Fuente: Elaboración propia.Figura 4 Tasas específicas de mortalidad de la región menor observadas y tipificadas y tasa específica de mortalidad de la región mayor (patrón)
Como se muestra en el gráfico, la curva tipificada sigue un comportamiento igual al de la curva patrón pero con un nivel más alto. Las inconsistencias en las tasas observadas de la región menor se corrigieron una vez tipificadas y por tanto se muestran resultados que pueden ser utilizados en análisis y comparaciones, así como a la hora de evaluar tendencias en la estructura de la mortalidad de ese territorio.
Consideraciones finales
El trabajo en pequeñas áreas generalmente implica que estamos ante poblaciones pequeñas. Sin embargo, en muchas ocasiones, aunque se trabaje con grandes bases de datos y grandes poblaciones, la estratificación de dicha población convierte a determinado grupo objeto de estudio en una población pequeña. Independientemente del número de eventos y de población, es importante observar el comportamiento de los indicadores para definir si estamos ante poblaciones pequeñas o no, aunque en ocasiones sea evidente que efectivamente es pequeña. Una vez identificado esto, es imprescindible saber que los datos observados pueden generar resultados que no son robustos y no se pueden interpretar desde una estimación directa de los indicadores. El método de corrección a ser utilizado para la estimación depende tanto de los datos disponibles como del objetivo del investigador, por tanto el primer paso es definir exactamente a qué pregunta se le dará respuesta y qué objetivo se quiere alcanzar con la estimación. Dentro de los métodos a utilizar se encuentra la tipificación indirecta, para el cual el primer paso es escoger bien el patrón a ser utilizado. Una buena selección del patrón disminuye los errores que se arrastran al realizar los supuestos del método y los resultados son más fieles a la realidad de la población objeto de estudio.
La tipificación indirecta es un método muy utilizado en demografía para estimar indicadores en ausencia de datos o cuando estos no son confiables. En el caso de la población pequeña, aunque se tiene el dato, este no puede ser utilizado pues el escaso número de eventos y los pequeños números de población no permiten hacer estimaciones directas. No obstante es importante recordar siempre que al aplicar este método se está suponiendo que la población en estudio tiene características semejantes al patrón escogido y esto es fundamental a la hora de interpretar los resultados. Aunque efectivamente se pueden estar introduciendo errores a la hora de hacer suposiciones, la aplicación del método permite realizar análisis precisos de los fenómenos y estudiar poblaciones donde es necesaria la información. Asimismo, a la hora de realizar comparaciones o trazar tendencias de un indicador a nivel local lo más importante es evaluar la eficacia del método y si este no fuera el más indicado buscar otras alternativas de estimación.
