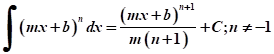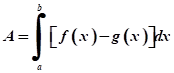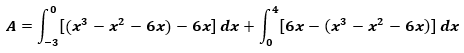Introducción
En la actualidad, los avances tecnológicos permiten hacer representaciones concretas del mundo real. Esto hace que se pueda comprender con mucha más precisión conceptos que, por su naturaleza abstracta, antes eran difíciles de entender. Ya es posible modelar procesos y estudiarlos en todas sus dimensiones. Se pueden realizar actividades mucho más interactivas usando recursos tecnológicos.
Se está observando que los nuevos recursos tecnológicos, en especial los informáticos, tienen una mayor significancia debido a que permiten realizar tareas complejas de una manera más rápida. Así como muchas ciencias hacen uso de las tecnologías para lograr nuevos avances, las Ciencias Pedagógicas buscan sistematizarse en los recursos tecnológicos para fortalecerse.
Camacho (2005), expresó que“desde la década de los 80, existen en el mercado diferentes programas que poco a poco han ido incorporándose en la enseñanza, y que en la década de los noventa aparecen algunos programas más específicos, con más capacidades tanto simbólicas como gráficas (Maple, Matemática, Matlab, Mathcad, Derive, etc.), que su uso se ha ido extendiendo en la enseñanza del Cálculo o Análisis Matemático”. (p. 97)
Navas (2007) menciona que “hay que pensar en los desafíos que tenemos con relación a los contenidos educativos en tiempo de la Web 2 o Web social, destacar la necesidad de trabajar sobre la producción colaborativa de contenidos educativos. Esta producción colaborativa puede ser usada para la construcción de elementos de carácter intelectual que apoyen el desarrollo de nuestros sistemas educativos actuales y futuros”.(p. 379)
Tomando en consideración lo que mencionan estos investigadores, se deben emplear en todo su caudal las potencialidades de los recursos tecnológicos existentes. En especial la matemática se vería beneficiada con las capacidades de los programas que grafican y calculan,y más aún si con la web se pueden diseñar objetos de aprendizajes que harán más comprensibles los contenidos de esta ciencia considerada como dura.
Muchos países han comprendido esta necesidad y están impulsando el uso de las Tecnologías de la Información y Comunicación (TIC) en la educación, y por tanto han ido incorporando su uso cada vez con mayor fuerza en los procesos de enseñanza- aprendizaje. La Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (2018), afirma en su página web que las tecnologías de la información y la comunicación pueden complementar, enriquecer y transformar la educación y añade que la tecnología puede facilitar el acceso universal a la educación y reducir por tanto las diferencias en el aprendizaje, apoyar el desarrollo de los docentes.
No obstante, el uso de las tecnologías en este proceso presenta una amenaza en la ciencia matemática, en concreto en el área de cálculo integral, ya que al permitir que las operaciones se realicen de una manera rápida se está perdiendo la fundamentación de los conocimientos; lo que interesa al alumno es el resultado y no el proceso, como consecuencia se observa que cuando el estudiante es cambiado de escenario, éste ya no responde de la misma manera que con el uso de la tecnología.
Desarrollo
Los países de América Latina y el Caribe presentan limitaciones de recursos tecnológicos y por tanto la educación en esta región se ve afectada.“La región de América Latina y el Caribe, se encuentra determinada por su ubicación de exclusión en el marco de brechas y asimetrías en las que ocurre la división internacional de los conocimientos, de la innovación tecnológica y de la revolución de la ciencia y de sus aplicaciones, y esto aparece día a día de manera contrastante y desalentadora para las instituciones educativas de la región, que se ven constreñidas a llevar a cabo procesos que tienen que ver más con la transferencia de conocimientos o con su imitación, que con la innovación y creatividad desde la perspectiva de una cultura propia y de una identificación clara de las prioridades sociales y económicas en beneficio de las mayorías de sus poblaciones”.(Gazzola& Didriksson, 2008)
Sin embargo, con estas limitaciones, se observa que particularmente ciertos países tratan de apegarse a normas y estandarizaciones que hacen, sino llegar al nivel de los países desarrollados, alcanzar sus logros para mantenerse localmente competitivos.
Investigadores del tema han hechos estudios sobre el impacto de las tecnologías en la Educación Superior en América Latina. “El impacto de las nuevas tecnologías por su parte, está contribuyendo a la globalización de la educación, permitiendo acortar las distancias, expandir la educación transfronteriza y las modalidades de educación en red, y al generar la educación virtual, viabilizar nuevas prácticas pedagógicas de simulación, de autoaprendizaje y de praxis, y una educación no presencial”.(Rama, 2006).
Con los resultados de estos estudios, las instituciones de Educación Superior en Ecuador proponen sus contingencias para estar actualizados con los nuevos métodos y recursos que exigen los planes de estudios.
La Educación Superior está enfrentando retos y desafíos que exigen que se planteen profundas transformaciones en su sistema de acuerdo a las tendencias y exigencias actuales. Los procesos de enseñanza-aprendizaje se ven obligados a incorporar las tecnologías de la información y comunicación (TIC) para hacer más eficiente el cumplimiento de sus objetivos.
En el Ecuador, las investigaciones en el uso de dichas tecnologías, realizadas en la Educación Básica y Media, ha provocado la ampliación investigativa a la Educación Superior, en particular en las modalidades a distancia.
Con la Educación a distancia surge la necesidad de usar medios tecnológicos. El desarrollo más importante de la educación superior virtual ocurre a partir de 1994, cuando el World Wide Web se perfecciona como medio de comunicación gráfico, con imágenes fijas y en movimiento y multimedia y se afirma como servicio telemático integrador de varios servicios telemáticos que se fueron desarrollando de manera independiente para efectuar diversas operaciones de información y comunicación en INTERNET (Silvio, 2004).
Es indudable que los recursos con tecnología de punta que existen hoy en día, facilitan la ampliación de la educación a lugares que por su geografía impiden el acceso físico del profesor; con gestión gubernamental se podrían financiar programas dirigidos a erradicar el analfabetismo, por ejemplo, y, siendo más puntuales, las instituciones educativas particulares pueden aportar de manera directa en este sentido.
En el III encuentro de Rectores de Universidades, realizado en el año 2014 en Río de Janeiro, se declaró que “las tecnologías digitales están provocando un trascendental cambio en el escenario educativo presente, al tiempo de que generan profundas transformaciones e innovaciones, en ocasiones disruptivas, en los modos de generación, acceso, reproducción, transmisión y acumulación de conocimiento”. (Ecuador. Universidad Laica Eloy Alfaro de Manabí, 2014, p. 18)
En este encuentro de rectores también se establece que debe haber trabajo en conjunto entre las universidades “para promover iniciativas orientadas a la investigación y el desarrollo de modelos de soporte y elaboración de contenidos educativos digitales; impulsar la formación continua con recursos en la Red; desarrollar programas educativos abiertos en línea (MOOCs)”(Ecuador. Universidad Laica Eloy Alfaro de Manabí, 2014, p. 18). Se observa que la tendencia sería que las universidades busquen la manera de cómo incorporar esta necesidad en sus programas educativos.
Los estudiantes de hoy en día están rodeados de tecnología, con los beneficios que esto significa, pero también con las dificultades que podrían incluir Trastornos de tipo adictivo, por tanto, este tipo de estudiante necesita un enfoque diferente del proceso enseñanza aprendizaje y es allí donde está el desafío. “Las actitudes, aptitudes, perfiles, habilidades, modos y formas de comunicación de las nuevas generaciones de estudiantes evolucionan rápidamente, planteando numerosos retos a las universidades”.(Ecuador. Universidad Laica Eloy Alfaro de Manabí, 2014, p. 15)
Usar las Tecnologías de la Información y Comunicación como medio en el proceso docente hace que contenidos que por su naturaleza son difíciles de asimilar, por ejemplo, la matemática, se presenten atractivos al aprendizaje y provoquen una motivación para enfrentarlos.
Los alumnos deben comprender que las herramientas tecnológicas son “instrumentos que ofrecen representaciones y relaciones entre objetos matemáticos con las que ellos pueden interactuar, dando una nueva dimensión a la construcción del conocimiento matemático”. (Lupiáñez & Moreno, 2001)
En todo el entorno educativo se debe concebir que “dado el desarrollo científico técnico de las Tecnologías de la Informática y las Comunicaciones (TIC) es factible el logro de una enseñanza desarrolladora” (Reyes, Cabrera, Estevés, & Jiménez, 2006). Todo es cuestión de darle el significado apropiado a los contenidos.
Las tecnologías por sí mismas no generan nuevas operaciones mentales, pero el uso adecuado de ellas puede permitir un dominio de operaciones mentales con las que el individuo ya cuenta.
Con los nuevos retos en la educación, “la generalización en el uso de las TIC no garantiza por sí sola la consecución de los objetivos perseguidos y es, por tanto, una condición necesaria pero no suficiente. Antes bien, dicha consecución pasa ineludiblemente por una profunda transformación de los fundamentos pedagógicos del sistema de enseñanza universitaria”.(Carrasco, Gracia, & Villasol, 2005)
Se deberá buscar el momento apropiado para usar la tecnología. “Las simulaciones son un buen ejemplo de la utilización de la tecnología para valorar con mayor precisión lo que un alumno puede hacer. En los escenarios reales que representa la simulación se exige al alumno que aplique las estrategias de resolución de problemas y las habilidades para resolverlos”.(Fernández & Cebreiro, 2003)
“Otra posibilidad que ofrecen las TIC, y que permite enriquecer el proceso de enseñanza dando una mayor participación al alumno en su proceso formativo, son las pruebas de autoevaluación. El alumno, mediante la realización de estas pruebas tiene un mayor control sobre su aprendizaje y puede autorregularlo”.(Fernandez & Cebreiro, 2003).
No cabe duda que si se emplearan las TIC para que el alumno se autoevalúe, por ejemplo, a través de la realización de un ejercicio de cálculo integral para su inmediata corrección, esto serviría para que no se formen los conceptos erróneos que tanto mal hacen a los contenidos que necesitan ciertas bases.
En matemática, los investigadores Iniguez & Vasquez (2011) plantean que “los docentes deberían utilizar la tecnología con el fin de mejorar las oportunidades de aprendizaje de sus alumnos, seleccionando o creando tareas matemáticas que aprovechen lo que la tecnología puede hacer bien y eficientemente”.(p. 20)
Si los estudiantes ingresan a la universidad con preparación y predisposición en el uso de las TIC, en materia de educación, esto facilita la labor del docente. Iñiguez & Vásquez (2001), con sus investigaciones en colegios han observado que “hay el convencimiento de la gran mayoría de los estudiantes que la aplicación de las TIC en matemáticas es una alternativa para mejorar su rendimiento académico en la asignatura y confían en que no será solo una herramienta de aprendizaje que le servirá para el colegio sino es una preparación en prácticas que se asemejan a los métodos de enseñanza que tendrá en el sistema universitario”.
Existe una corriente académica importante en la educación superior que plantea la necesidad de desarrollar en los estudiantes universitarios distintos tipos de conocimientos y habilidades para poder actuar de manera competente en la llamada sociedad de la información y el conocimiento(Badia, 2006).
Barbera &Badia (2004), menciona que “con respecto a los factores relacionados con las tecnologías, hay suficientes evidencias que demuestran que las TIC pueden ser elementos de innovación didáctica en las instituciones educativas”. Entonces no hay que dejar pasar esta oportunidad para fortalecer los procesos de enseñanza aprendizaje. Las instituciones deben comprometerse a tal punto que exijan que las asignaturas innoven usando las TIC y se fortalezca el componente medios.
Los avances de la inteligencia artificial en este campo, están otorgando a profesores y estudiantes nuevas oportunidades, donde el proceso educativo, respetando la diversidad, permita la adquisición de competencias que han sido difíciles de alcanzar en la educación tradicional, tales como: aprendizaje autodirigido, gestión del propio conocimiento, automotivación y autodirección (Vílchez, 2007).
En cualquier proceso de tutorización online, la comunicación se constituye como uno de los elementos que aporta mayor significatividad y calidad a los procesos educativos (Llorente, 2006). Esto significa que ahora podemos atender de una manera muy rápida y eficiente las necesidades que presentan los programas de estudios y motivar a los aprendices, de tal forma que sus problemas sean resueltos casi en tiempo real y pasar a buscar nuevos conocimientos.
En la actualidad, los diferentes cambios en los modelos de comunicación han permitido evolucionar desde modelos unidireccionales de comunicación en los que habitualmente existe un emisor (profesor o material didáctico) que ofrece la información a un receptor (normalmente el alumno) que la procesa, a modelos de comunicación más interactivos y dinámicos que persiguen que el receptor se convierta en emisor de mensajes, tanto de forma individual como colectiva.
El desarrollo de la microelectrónica, la informática y las telecomunicaciones ha generado grandes cambios en el espacio educativo. Si bien se trata de tecnologías que no nacieron en esta área, su apropiación paulatina ha impulsado innovaciones tanto en lo académico como en lo administrativo, lo que se ha evidenciado con mayor fuerza en el nivel superior (López, 2008).
La integración de las TIC en la institución educativa provocará transformaciones esenciales en todos sus procesos, y entre ellos la razón de ser de la institución: el proceso de enseñanza aprendizaje, que se configura en un modelo pedagógico con nuevas cualidades.
Pero la realidad es que integrar la tecnología en el proceso de enseñanza aprendizaje es algo más complejo. Este proceso implica un análisis riguroso de los objetivos educacionales, una comprensión real del potencial de las tecnologías, una consideración de los prerrequisitos y estudio de la efectividad de las TIC para la Educación y las perspectivas de este proceso en la dinámica de los cambios que ocurren en la institución docente.
Hoy parece que una gran parte de los problemas de los sistemas de formación se solucionarán con el llamado B- learning o blended learning (aprendizaje mixto, híbrido o combinado).
Introducir nuevas tecnologías no es suficiente, se requieren cambios profundos en la estructura académica y administrativa para lograr los fines deseados (López, 2008). Las instituciones deben tomar en serio este desafío. Debe ser un compromiso institucional, para que a largo plazo se den estos fines deseados.
Sangra & González (2004), citado por López (2008), señalan "la integración de las TIC ha de hacerse de forma explícita, planificada y sistemática, implicando a la organización en su conjunto e involucrando a sus miembros individual y colectivamente. Solo entonces podrán convertirse en un factor de cambio y de mejora de la universidad". (p. 76)
El uso de las TIC en el proceso docente debe permitir lograr el aprendizaje de una manera más eficiente. Lo que no debe ocurrir es que se crea que la tecnología sustituye al profesor y, peor aún, que los estudiantes piensen que ya no hay que pensar para resolver los problemas porque una herramienta tecnológica lo hace por ellos.
Lupiáñez & Moreno (2001), puntualizan que “es crucial entender que los objetos que aparecen en la pantalla y que manipula la calculadora no son objetos concretos ni objetos del mundo matemático formal: son objetos virtuales que están en la interface que separa el mundo conceptual de las matemáticas del mundo de los objetos concretos”.
Una situación que las autoridades de la educación deben considerar es que puede haber un uso no concientizado de la tecnología. Que se llegue a pensar que la tecnología es la panacea del problema de la educación. “Un argumento que se esgrime habitualmente en contra del empleo de tecnología en la enseñanza de las matemáticas es que se abandona y olvida lo que se hace con papel y lápiz, y eso va en perjuicio de la calidad en la formación. Creemos que hay que entender la instrumentación de las tecnologías informáticas en la enseñanza de las matemáticas, como un proceso de enriquecimiento, no como sustitución, tratando de mejorar capacidades cognitivas, no de sustituirlas”. (Lupiáñez & Moreno, 2001)
Los procesos cognitivos deben generarse con el empleo de las TIC. Si el proceso de enseñanza-aprendizaje está mediado fundamentalmente por las TIC, se deberá lograr que la tecnología sea percibida como un medio que aporta a este fin.
Que no se crea que el fin es que se aprenda a utilizar las herramientas tecnológicas, más bien hay que lograr que estas herramientas sean conceptualizadas como un aporte a la solución cuando las tareas resultan extensas, laboriosas o complejas, que han hecho que los estudiantes se desmotiven y hasta que abandonen su objetivo.
La Organización Mundial de la Salud (OMS) ha señalado que una de cada cuatro personas sufre de trastornos vinculados con las nuevas tecnologías. De hecho, en la Clasificación internacional de las enfermedades (CIE), tratado fundamental de la OMS para identificar estadísticas y problemas de salud en el mundo; en su versión número once, a publicarse en enero de 2022, ha incluido, por ejemplo, en la sección de Trastornos de la adicción precisamente la adicción a los videojuegos, actividad de absoluta preferencia para cada vez más jóvenes cuando de uso de tecnología se trata.
Puede ocurrir que con el empleo de la tecnología se abandone actividades del desarrollo de procesos cognitivos que de tan buena manera han favorecido la formación académica del alumno y más aun de las matemáticas.
La elaboración de nuevas representaciones mentales implica una actividad cerebral que codifica la información a través de nuevos procesos cognitivos, lo que requiere de varias redes neuronales interconectadas.
Se observa que los alumnos actuales no pueden hacer cálculos sencillos que los estudiantes de generaciones anteriores sí lo hacían. Esto nos hace dudar de emplear las TIC. Es posible que las TIC en lugar de contribuir al aprendizaje de los estudiantes lo están perjudicando. Al usar la tecnología para cálculos operatorios, el estudiante ya no desea aprender los principios básicos que hay tras esta operatoria y se pierde la fundamentación que todo problema matemático debe tener.
Según Camacho (2005), el impacto de estas tecnologías ha llevado a dedicar un espacio de discusión e investigación emergente, en el que han surgido elementos teóricos que nos ayudan a interpretar las dificultades y potencialidades que aparecen al introducir las TIC en el aula.
Investigadores en educación concluyen en sus trabajos que existe una percepción de aislamiento, deshumanización y frialdad en las interacciones entre las personas que utilizan una computadora, tanto en la práctica profesional como en la vida cotidiana (Peinado, 2011).
Es así que hay una tendencia cada vez mayor a que los jóvenes interactúen con facilidad en sus redes sociales mientras que al mismo tiempo van perdiendo, o no aprenden, habilidades sociales básicas para interactuar en la vida real.
Si no se hace un uso racional de las TIC en los procesos educativos, se reflejará un impacto negativo en el avance de la enseñanza-aprendizaje de la Matemática y en particular del Cálculo Integral. Todo dependerá de la habilidad del profesor para que el alumno no se vea sólo frente a una máquina que le proporciona procedimiento mas no formas de pensar.
El aprendizaje matemático no es meramente operacional, desde el punto de vista de las neurociencias se afirma que también es semántico, por lo que, así como es importante la comprensión de conceptos tales como cantidad, también lo es su proyección espacial, por lo que el papel del docente en el aula es imprescindible para la comprensión y retención de los nuevos conocimientos. En las nuevas teorías del aprendizaje se afirma que pensamos no sólo con la ayuda del lenguaje y de los símbolos sino también a través de los sentidos, y el uso de tecnologías representan exposición a estímulos sensoriales constantes.
Para lograr mitigar el impacto negativo en el proceso docente educativo en la enseñanza de Cálculo Integral se ofrece una propuesta didáctica que consiste en una integración efectiva de profesor-alumno-conocimiento-tecnología, relacionados todos con el contexto social, en el proceso de enseñanza aprendizaje del Cálculo Integral de la asignatura Matemática II de la Universidad Santa María Campus Guayaquil.
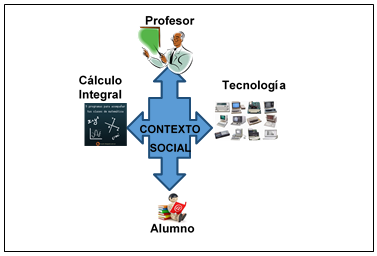
Los investigadores Vera & Flanklyn (2005), definen un esquema básico para representar el acto educativo. A este esquema le llaman Polígono Didáctico. Los elementos principales (docente, alumno, cultura, tecnología y la realidad social) los ubican en los vértices de un polígono y mencionan que existe un conjunto de interrelaciones que se presentan cuando dichos factores interactúan en una situación hipotética y/o real en el acto educativo.
En un principio se analizaban los modelos empleando un Triángulo Didáctico, docente-alumno-conocimiento, pero con los nuevos desafíos es necesario ampliar el triángulo a un polígono, mencionan Vera & Flanklyn (2005). Los conocimientos se amplían a cultura matemática y se incorpora la tecnología. Esto da a lugar a que se considere las interrelaciones y la realidad social.
La propuesta que se sugiere aquí está basada en el polígono didáctico de Vera& Flanklyn, el aporte consiste en esquematizar plenamente las relaciones entre los componentes personológicos y los no personológicos del proceso de enseñanza-aprendizaje del Cálculo Integral de la asignatura Matemática II.
Se plantea que el proceso de enseñanza-aprendizaje tiene cuatro componentes: profesor, alumno, conocimiento (Cálculo Integral en este caso) y la tecnología; y, todos enmarcados en un contexto histórico-social (Figura 1).
El profesor dispone de la base epistemológica del Cálculo Integral y de la tecnología como medio. El profesor puede impartir la clase con o sin recurso tecnológico, sin embargo, si imparte la clase tradicionalmente estará en desventaja con el avance en la cultura tecnológica que poseen los estudiantes.
La tecnología debe actuar como objeto motivador del proceso y aquí está el desafío del docente. Su diseño debe captar la atención de las personas involucradas en el proceso. Hacer de la tecnología un reactivo motivante es el gran desafío para el profesor.
La atención es otro recurso importante que involucra a la memoria de trabajo. Por eso, despertar la atención del estudiante es de vital importancia. El docente debe ser creativo e innovador para aumentar la motivación y estimular los niveles dopaminérgicos. A mayor concentración, menor es la ansiedad (en este caso, de la ansiedad matemática) (Mogollón, 2010). En este sentido el uso de las TIC representa una disyuntiva puesto que con su uso es posible captar en una primera instancia la atención del estudiante, pero al mismo tiempo, en su uso cotidiano puede generar distractores continuos. Se debe por tanto motivar a los estudiantes al correcto uso de la tecnología para facilitar la memoria de trabajo con estos recursos.
El alumno atiende y codifica la información, luego debería planificar la solución del problema. Podrá recurrir a su bagaje de conocimientos, al entorno social (puede ser asistido por el profesor o por alguno de sus compañeros) y a la tecnología disponible.
El alumno debe ser capaz de resolver los ejercicios o los problemas, si es que existen ejercicios o problemas, debe ser capaz de almacenar la información y recuperarla cuando sea necesaria. Aquí también entraría la tecnología. Habiendo estrategias de refuerzo (actividad directa) usando la tecnología habría un mejor nivel de asimilación de los conocimientos.
Además, como se ha anotado anteriormente, todo este proceso facilitará también la disminución de la ansiedad y, en casos más graves, la fobia matemática, ya que el estudiante estará haciendo uso de recursos que le son familiares y atractivos, y sus esfuerzos se verán rápidamente recompensados mediante el refuerzo con cada acierto, pero a la vez, en caso de errores, no deberá enfrentar la presión social del acierto inmediato, ya que podrá de manera individual aprender de sus errores; no obstante, dichos logros individuales deberán ser reforzados por el docente en el aula de clases, así como la corrección de errores y la validación de los mismos como parte del proceso de aprendizaje.
La estrategia consistió en aplicar la propuesta de las cuatro vertientes al grupo experimental. Se consideró temas de Técnicas de Integración e Integral definida. Por ejemplo:
TEMA 1. “Integral Indefinida: Integración directa”
Vertiente 1: Contenido para Integración Directa. Los conocimientos previos que deberían tener los estudiantes serían temas algebraicos como ley de los exponentes, operaciones con fracciones y simplificación de expresiones en general. Los demás aspectos a considerar serían las fórmulas y propiedades de las integrales.
Vertiente 2: Tecnología: Software libre para diagnosticar los conocimientos previos de los estudiantes. Google Drive proporciona una herramienta poderosa para hacer test online autocorregibles (Figura 2). Esto es motivante para el alumno, debido a que es un ambiente no tradicional. Además, que permite autoevaluar sus niveles de entrada. El alumno recibe su puntuación y una explicación de la solución de los ejercicios. Para la explicación, el software da la opción de utilizar recursos multimedios. Un video puede ser empleado para esta explicación o un texto bien detallado en muchas ocasiones es suficiente.
Para actividades de refuerzo recomendamos utilizar el software SYMBOLAB que servirá de tutor del estudiante. Este software en una calculadora que proporciona la solución paso a paso de los ejercicios.
Para anuncios de actividades, se puede utilizar el correo electrónico o las redes sociales como WhatsApp o Facebook.
Vertiente 3: Profesor: El profesor presenta el tema en una sesión presencial, preferiblemente en una clase colaborativa en donde debe lograr que el estudiante construya el concepto.
Aquí se aprovecha la oportunidad para hacer énfasis en situaciones generales. Por ejemplo, para la fórmula , considerar una función
, considerar una función  . Hacer notar que tenemos
. Hacer notar que tenemos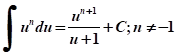
Esta generalización la puede lograr con ayuda del grupo o con ayuda del profesor. Se sugiere realizar un taller grupal en donde los estudiantes resuelven algunos ejercicios conceptuales para ir logrando el andamiaje que menciona Bruner.
El profesor debe inducir a que el estudiante practique en el software SYMBOLAB, con algunos ejercicios propuestos. Se sugiere diseñar un test online de diagnóstico sobre integración directa para observar el progreso del alumno. Luego realizar una evaluación presencial para confirmación del nivel de asimilación.
Vertiente 4: Alumno: El alumno, al momento del diagnóstico de los conocimientos previos, reactiva su bagaje de conocimientos, en este caso la ley de los exponentes y simplificación de expresiones algebraicas en general. Y si existe deficiencia, es la oportunidad de lograr el nivel requerido de entrada.
En la sesión presencial, recibe la información, la codifica para lograr interiorizarla. Aquí debe demostrar que posee una buena percepción de simbología matemática, es decir debe estar en la capacidad activa para la captación y organización de la información para darles sentido a través de la organización, integración e interpretación de la información recibida. Esta información debe quedar almacenada en su memoria de largo plazo para poder recuperarla cuando sea necesario.
Este almacenamiento y recuperación es más efectivo si el alumno descubre el conocimiento. En el caso del ejemplo, si logra generalizar y concluir que:
Los refuerzos online realizados por los estudiantes deben ser con compromiso y responsabilidad.
TEMA 2. “Cálculo de áreas de regiones planas”
Vertiente 1: Contenido. Los estudiantes deberían tener conocimientos sobre gráficas de funciones en dos dimensiones y deben poder identificar regiones planas limitadas por curvas en coordenadas cartesianas. El contenido propio del tema sería la definición de Integral Definida y su aplicación en cálculo de áreas de regiones planas.
El estudiante debe saber calcular antiderivadas (Integral Indefinida)
Vertiente 2: Tecnología: Software libre para diagnosticar los conocimientos previos de los estudiantes.Con Google Drive se puede elaborar una prueba donde se diagnostique conocimientos de gráficas de funciones. El diagnóstico debe ser muy conceptual, de tal manera que, aunque la tecnología permita obtener gráficas, el estudiante pueda llegar a conclusiones sobre regiones planas y pueda obtener puntos de intersecciones entre curvas.
Existe un sinnúmero de graficadores de libre descarga que pueden ser útiles: Maple, Winplot, Graph, Geogebra, entre otros. Se recomienda el Graph debido a que para graficar no se requiere manejo de programación o comandos y se puede obtener valores de áreas de algunas regiones planas.
También se recomienda emplear el graficador online FOOPLOT que no requiere instalarse en el Computador y pueden elaborarse las gráficas de manera rápida y directa igual que el Graph.
Para anuncios de actividades, se puede utilizar el correo electrónico o las redes sociales como WhatsApp o Facebook.
Vertiente 3: Profesor: El profesor presenta el tema presencialmente, preferiblemente en una clase colaborativa en donde debe hacer que el estudiante construya el conocimiento. Ir desde el área bajo una curva ubicada en el primer cuadrante hasta que logre plantear la integral correspondiente para cualquier región plana. Aquí puede hacer uso del software GEOGEBRA (Figura 3). Donde además se aprovecha para reforzar el concepto de Integral Definida.
En el trabajo colaborativo se debe lograr que los estudiantes encuentren áreas de regiones en ejercicios propuestos por el profesor.El profesor debe inducir a que el estudiante practique en el software que más se acomode. Se sugiere diseñar un test online de diagnóstico sobre cálculo de áreas para observar el progreso del alumno. Luego una evaluación presencial para confirmación del nivel de asimilación.
Vertiente 4: Alumno: El alumno debe ser capaz de elaborar gráficas sin tecnología y con tecnología para verificar sus resultados y no continuar en procesos irrelevantes.
En la sesión presencial, recibe la información (atiende), la codifica para lograr almacenarla y recuperarla cuando sea necesario. Trabaja colaborativamente.
Es importante que el estudiante pueda plantear integrales definidas para regiones generales (figura 4). Se requiere que los refuerzos online post clase realizados por el alumno sean con compromiso y responsabilidad.
La expresión anterior representa el área sombreada.
Utilizando otro de los softwares mencionados anteriormente, el Maple 18, se puede calcular el valor del área:
Una vez realizado el cuasi experimento se realizó una prueba on-line a través de google drive, tanto al grupo de control como al grupo experimental. Para el análisis estadístico se empleó el software SPSS.En la media del grupo experimental y de control se observa una diferencia de 1.94 puntos (Tabla 1) (6.33 - 4.39).Esto da para pensar que la estrategia ha dado resultados. Lo debemos demostrar estadísticamente.
Tabla 1 Estadísticos de grupo.
| GRUPOS | N | Media | Desviación típica | Error típico de la media | |
|---|---|---|---|---|---|
| CALIFICACIONES | GRUPO EXPERIMENTAL | 27 | 6,33 | 2,219 | ,427 |
| GRUPO DE CONTROL | 18 | 4,39 | 2,173 | ,512 |
Se realizó un análisis de normalidad a las calificaciones empleando SPSS para poder luego aplicar l. prueba t-student para la diferencia de medias.
Tabla 2 Pruebas de normalidad.
| Kolmogorov-Smirnova | Shapiro-Wilk | |||||
|---|---|---|---|---|---|---|
| Estadístico | gl | Sig. | Estadístico | gl | Sig. | |
| CALIFICACIONES | ,121 | 45 | ,096 | ,955 | 45 | ,075 |
| Corrección de la significación de Lilliefors | ||||||
La tabla 2 muestra que las calificaciones se comportan de manera aproximadamente normal debido a que la significancia p=0.096 mayor a 0.05, empleamos Kolmogorov-Smirnov debido a que la muestra es de tamaño 45. Por tanto, podemos proceder a realizar la prueba t.
Tabla 3 Prueba de muestras independientes.
| Prueba de Levene para la igualdad de varianzas | Prueba T para la igualdad de medias | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F | Sig. | t | gl | Sig. (bilat) | Diferencia de medias | Error típ. de la diferencia | 95% Intervalo de confianza para la diferencia | ||||
| Inf | Sup | ||||||||||
| CALIFICACIONES | Se han asumido varianzas iguales | ,001 | ,975 | 2,903 | 43 | ,006 | 1,944 | ,670 | ,594 | 3,295 | |
| No se han asumido varianzas iguales | - | - | 2,916 | 37,119 | ,006 | 1,944 | ,667 | ,593 | 3,295 | ||
En la tabla 3 se puede observar que la prueba de Levene da una significancia de 0.975 que es mayor a 0.05, esto nos indica que no hay diferencia de las varianzas entre los grupos por lo cual concluimos que tenemos grupos homogéneos.
Finalmente, la prueba t nos da una significancia de 0.006 que es menor que 0.05 lo cual nos indica que hay diferencia entre las medias de los grupos, por tanto, concluimos que el método aplicado al grupo experimental ha dado resultado.
Conclusiones
En la enseñanza del Cálculo Integral, y de la Matemática en general, se deben emplear en todo su potencial los recursos tecnológicos disponibles para lograr una comprensión plena de temas abstractos que antes eran difíciles de ilustrar.
La presencia del profesor no debe ser discutible. Sin embargo, el profesor del siglo XXI debe estar capacitado en el uso de las TIC para hacer los diseños correspondientes y lograr resultados más efectivos.
El proceso de enseñanza aprendizaje es dinámico, lograr la integración de estas cuatro vertientes alumno-profesor-conocimiento-tecnología es el desafío del día a día de la labor docente.
El estudiante debe estar en continua actividad académica conceptual para el logro de desarrollo de habilidades y llegar a un meta-aprendizaje.
Los resultados que se mostraron corresponden proporcionan evidencia estadística con una confianza del 95% de que la propuesta da resultado. Se pudo constatar con la propuesta formulada que los estudiantes mostraron entusiasmo, conocimiento y desarrollaron habilidades en el cálculo integral con la nueva metodología.