Introducción
En el proceso de enseñanza - aprendizaje de la Geometría los medios de enseñanza ocupan importantes funciones porque garantizan que los escolares puedan apropiarse de los conceptos y procedimientos geométricos, a partir de percepciones visuales y táctiles.
Dentro de los medios de enseñanza más utilizados en las clases de Geometría se encuentran los objetos concretos (objetos del mundo real y modelos geométricos), las representaciones gráficas, ilustraciones y los software educativos.
Otros medios de enseñanza que tienen gran importancia en el proceso de enseñanza - aprendizaje de la Geometría son el Tangram y el Geoplano. Esta importancia está dada en que a partir de las actividades de manipulación y experimentación que con ellos se realizan los escolares pueden adquirir las propiedades y características de las figuras geométricas.
El Tangram es un rompecabeza, que tiene su origen en la antigua cultura china. Existe una gran variedad de Tangram pero el más utilizado en el contexto educativo es el obtenido a partir de un cuadrado que consta de 7 piezas (5 triángulos, 1 cuadrado y 1 paralelogramo).
El uso del Tangram en el proceso de enseñanza - aprendizaje de la Geometría en la Educación Infantil favorece la introducción de los conceptos geométricos de figuras planas y con su ayuda se puede contribuir, además, al desarrollo de habilidades geométricas en los escolares.
Por su parte, el Geoplano es un medio de enseñanza creado, en 1921, por el profesor italiano Caleb Gattegno con el objetivo de facilitar a los niños, desde cinco años, el estudio de las relaciones geométricas y proporcionar en ellos la experiencia en esa materia (Piaget, et al., 1968). Consiste en un tablero de madera, con forma ortoédrica, en el que se disponen clavos, que conforman cuadrículas, para representar con gomas, de diferentes colores, figuras y movimiento geométricos. Gattegno presentó este medio de enseñanza en la primera publicación conjunta de la Comisión Internacional para la mejora de la enseñanza de las Matemáticas en 1961.
En la Educación Infantil resulta muy interesante el carácter manipulativo de este medio de enseñanza. A partir de su uso los escolares comienzan a representar, primeramente, figuras de manera libre y en diferentes posiciones, para posteriormente adentrarse en el conocimiento de las figuras geométricas; armar y desarmar figuras, conocer los conceptos de perímetro, área y los movimientos geométricos.
Algunos autores, como Salazar (2000); Verdugo, et al., (2000); y Blanco (2005), han destacado la importancia de la utilización del Tangram y el Geoplano en el proceso de enseñanza - aprendizaje de la Geometría y han realizado sus propuestas para la elaboración y utilización de estos medios de enseñanza.
Desarrollo
Teniendo en cuenta las experiencias y las insuficiencias (León González & Barcia Martínez, 2016), que se presentan en el proceso de enseñanza - aprendizaje de la Geometría en la escuela primaria, los autores han decidido ofrecer a los docentes un procedimiento para confeccionar un Tangram y un Geoplano utilizando las nociones geométricas de igualdad de figuras, paralelismo y perpendicularidad.
Finalmente, se exponen, a manera de ejemplos, un conjunto de actividades que pueden utilizarse en el proceso de enseñanza - aprendizaje de la Geometría para el desarrollo de habilidades geométricas utilizando estos medios de enseñanza.
1. Procedimiento para la construcción de un Tangram.
Materiales necesarios: cartulina, regla, cartabón, colores o tempera y tijera.
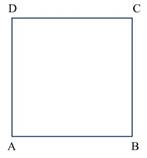
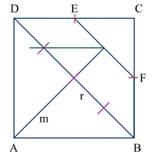
1. Se debe dibujar en la cartulina un cuadrado de 20 cm de lado (el lado del cuadrado puede ser de otra longitud) y denotarlo con las letras A, B, C y D (Figura 1).
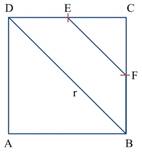
2. Después se traza una recta r, con la regla, de forma tal que divida ese cuadrado en dos triángulos iguales (Figura 2).
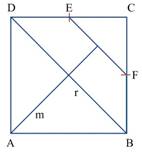
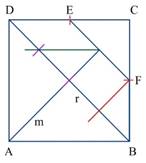
3. Se sitúan los puntos E y F, respectivamente, en el medio de los segmentos DC y BC y se traza un segmento que una dichos puntos y sea paralelo a la recta r (Figura 3).
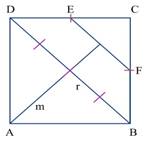
4. Se traza una recta m, perpendicular al segmento EF, de forma tal que corte a la recta r y que pase por el punto A (Figura 4).
5. Se divide el segmento BD formado ena recta r, con la regla, en cuatro partes iguales (Figura 5).
6. Se traza la recta verde que se muestra a continuación, paralela al segmento DE (Figura 6).
7. Por último, se traza esta recta roja, perpendicular a la recta r y se recortan, cada una de las piezas que lo conforman (Figura 7).
2. Procedimiento para la construcción de un Geoplano.
Materiales necesarios: Pedazo de madera, un lápiz, una regla y un cartabón, veinticinco clavos y un martillo.
1. En una tabla cuadrada de 30 cm de lados (puede variar igual la longitud del lado del cuadrado) se divide su lado izquierdo en seis partes iguales y se trazan cinco rectas paralelas (Figura 8).
2. Luego se divide la parte superior de la tabla en seis partes iguales y se trazan cinco rectas paralelas que corten a las rectas anteriores perpendicularmente y que formen cuadrados (Figura 9).

Fig. 9 Trazado de cinco rectas paralelas que cortan perpendicularmente a las rectas anteriormente trazadas.
3. Por último, se colocan cada uno de los clavos en el punto donde se cortan las rectas (Figura 10).
3. Ejemplo de actividades que pueden ser realizada con el uso del Tangram y el Geoplano.
A continuación se sugiere, a manera de ejemplo, un conjunto de actividades que pueden ser desarrolladas con ayuda del Tangram y el Geoplano en el proceso de enseñanza - aprendizaje de la Geometría en la Educación Infantil.
I. Ejemplo de actividades que pueden ser realizadas con el uso del Tangram.
Ejemplo 1
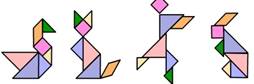
Construye con tu Tangram las siguientes figuras:
La realización de actividades de reproducción de figuras con las piezas del Tangram, utilizando un modelo, constituye la base para que los escolares desarrollen su creatividad al representar nuevas figuras conocidas por ellos. Estas actividades pueden ser realizadas por los escolares desde los primeros grados de la Educación Infantil. Desde este momento el docente debe insistir en que los escolares aprendan a colocar y manipular las piezas, en diferentes posiciones. Podrían añadirse, para ser conformadas por los escolares, la representación de algunas figuras geométricas.
Ejemplo 2
Observa las siguientes piezas del Tangram y señala, marcando con una equis (X), la respuesta correcta. Argumenta.
Tiene cuatro triángulos, un cuadrado y un rombo.
Tiene cinco triángulos y dos paralelogramos.
Tiene cinco triángulos y dos cuadrados.
En la realización de esta actividad resulta importante que los escolares dominen las propiedades de los paralelogramos y apliquen la relación entre conceptos.
Ejemplo 3
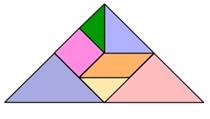
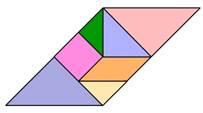
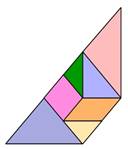
Transforma el siguiente triángulo en un trapecio moviendo al menos una de sus piezas.
Actividades similares a estas propician en los escolares el desarrollo de su imaginación, constancia y paciencia. Por otro lado, profundizan en la relación entre conceptos geométricos. Por ejemplo, moviendo solamente una de las piezas se obtiene un paralelogramo, como muestra la figura de la izquierda; pero también se obtiene un trapecio isósceles, tal y como muestra la figura de la derecha.
Ejemplo 4
En el Tangram compara la longitud del lado del cuadrado y la de los lados iguales en los triángulos grandes. Analiza la siguiente situación y marca con una equis (X), la respuesta correcta.
……Los lados iguales en los triángulos grandes tienen la misma longitud que el lado del cuadrado.
…… Los lados iguales en los triángulos grandes miden el doble de la longitud del lado del cuadrado.
……La longitud del lado del cuadrado es el doble de la de los lados iguales en los triángulos grandes.
Esta actividad puede constituir la motivación para el tratamiento del contenido perímetro. La comparación podría realizarse con tiras de papel o un instrumento de medición y trazado. Asimismo, podría indicársele a los escolares que comparen, indistintamente, la longitud del lado del cuadrado con la longitud del lado mayor en el triángulo mediano, que mide el doble; con la longitud de los lados iguales en los triángulos pequeños, que son iguales; finalmente con la longitud de un par de lados opuestos en el paralelogramo, que también es la misma.
Ejemplo 5
Mide con la regla la longitud de los lados de las piezas del Tangram y determina su perímetro.
Al darle solución a esta actividad se considera necesario que los escolares midan con la regla la longitud de cada una de las figuras que conforman el Tangram y que dominen el procedimiento para determinar el perímetro.
Ejemplo 6
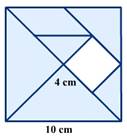
Calcula el área de la parte que ha sido sombreada en este Tangram.
Para calcular el área de la parte que ha sido sombreada en el Tangram los escolares determinarán el área del mayor de los cuadrados y la del menor; seguidamente deberán hallar la diferencia entre estos dos cuadrados, estableciendo la relación parte - todo.
II. Ejemplo de actividades que pueden ser realizadas con el uso del Geoplano.
Ejemplo 1
Representa en tu Geoplano las siguientes figuras geométricas:
Actividades como estas sirven de condiciones previas para la representación de nuevas figuras geométricas en la que los escolares posteriormente descubrirán cómo varían las propiedades geométricas de las figuras luego de mover algunos de sus puntos.
Ejemplo 2
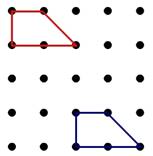
Selecciona cuál de los siguientes procedimientos debes seguir para trasladar en el Geoplano la figura azul hasta la posición que ocupa la figura roja.
……La muevo 3 unidades hacia arriba y 1 a la izquierda.
……La muevo 3 unidades hacia la izquierda y 2 hacia arriba.
……La muevo 2 unidades hacia la izquierda y 3 hacia arriba.
Actividades como estas garantiza que los escolares comiencen a familiarizarse con el movimiento de traslación de manera intuitiva. Se considera necesario que de forma previa se representen traslaciones en un mismo sentido y dirección, en papel cuadriculado.
Deben recordarse además las propiedades estudiadas de este movimiento: todos los puntos de una figura se mueven a una misma distancia y las figuras luego de trasladarse no cambian ni su forma, ni su tamaño.
En la solución de esta actividad debe destacarse que la figura roja puede obtenerse, a partir de la azul, mediante otros procedimientos como: se mueve tres unidades hacia arriba y dos a la derecha, etcétera.
Por otra parte, es importante que los escolares dominen que cuando se traslada una figura se realiza en un mismo sentido y dirección.
En este caso se han definido vectores de traslación usando un par ordenado.
Ejemplo 3
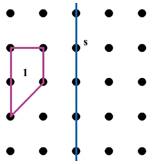
Representa en tu Geoplano la siguiente situación. Halla la imagen del cuadrilátero 1 por reflexión de eje s.
En la solución de esta actividad los escolares deben aplicar las propiedades de la reflexión: Un punto y su imagen determinan un segmento perpendicular al eje de reflexión y ambos están a igual distancia del eje.
Se debe insistir en que los escolares comprendan que en este movimiento las propiedades de forma y tamaño, al igual que en el resto de los movimientos, permanece. No obstante, el reflejo de la imagen queda invertido con respecto a la posición inicial de la figura.
Ejemplo 4
Calcula el perímetro de este polígono considerando que el lado de cada cuadrícula es de 5 cm.
Al solucionar actividades similares a esta los escolares deben determinar la cantidad de veces que el contorno de este polígono contiene la longitud del lado de la cuadrícula unidad. El contorno del polígono contiene 12 veces la longitud del lado de la cuadrícula unidad; en este caso el perímetro del polígono es 60 cm.
Ejemplo 5
Determina el área total de la figura considerando que el área de una cuadrícula es de 25 cm2.
Para calcular el área total de esta figura se debe determinar la cantidad de veces que la misma contiene el área de la cuadrícula unidad. La figura contiene 12 cuadrículas unidad. Luego el área total de la figura es 300 cm2.