Introducción
El cuadernillo que se pone a disposición, ha sido elaborado con el fin de ser utilizado para el desarrollo de competencias matemáticas en el grado séptimo de la Educación Básica Secundaria, de acuerdo con los Lineamientos Curriculares (Ministerio de Educación Nacional de Colombia, 1998), y los Estándares Básicos de Competencias (Ministerio de Educación Nacional de Colombia, 2006). Contiene variados ejercicios los cuales han sido diseñados sobre las recomendaciones hechas por la Organización para la Cooperación y el Desarrollo Económico (2005), que le servirán de ayuda para el desarrollo de competencias matemáticas de comunicación, representación y modelación; planteamiento y resolución de problemas; y razonamiento y argumentación; en situaciones que no abordan las competencias de manera aislada, sino de forma integrada. Las mismas, son coherentes con los indicadores de desempeño definidos para los niveles de desarrollo de cada competencia (Gómez, 2019).
Para la competencia comunicación, representación y modelación, se proponen actividades que demuestran como la matemática puede ser utilizada directamente o indirectamente en eventos de la vida real; las mismas, favorecen la búsqueda de alternativas de solución a un problema, contribuyendo al desarrollo de los otros grupos de competencias.
Con la ejecución de estas actividades, se espera que el estudiante describa y represente situaciones cuantitativas o de variación en diversas representaciones y contextos. En el planteamiento y resolución de problemas las actividades tienen como finalidad crear la capacidad en los estudiantes para formular problemas a partir de situaciones dentro y fuera del contexto de las matemáticas; desarrollar y aplicar diferentes estrategias para la solución de problemas; demostrar lo razonable o no de una respuesta obtenida; así como generalizar soluciones y estrategias para dar solución a nuevas situaciones problémicas. Se espera con el desarrollo de las actividades que el estudiante utilice diferentes modelos y estrategias en la solución de problemas con contenido numérico y variacional; que aplique estrategias geométricas o métricas en la solución de problemas; y que utilice distintas estrategias para la solución de problemas que involucren conjuntos de datos estadísticos, presentados en tablas, diagramas de barras, diagramas circulares y pictogramas.
En cuanto al Razonamiento y argumentación, se busca que los estudiantes hagan predicciones y conjeturas, den explicaciones coherentes y respuestas posibles, validen o invaliden conclusiones; y ayuden a comprender que las matemáticas no son simplemente procesos aburridos de memorización sin sentido. Con el desarrollo de las actividades propuestas para este grupo de competencias, se espera que el estudiante pueda justificar o refutar una opinión, elegir entre diferentes opciones o explicaciones, bajos criterios racionales que permitan valorar que la opción que se ha tomado es la adecuada. Abarca el seguimiento y la valoración de cadenas de argumentos matemáticos de diferentes tipos; son un conjunto de habilidades, conocimientos y actitudes encaminadas a la explicación de un determinado proceso, proposición, planteamiento, teoría, suceso, fenómenos naturales y sociales.
Las actividades pretenden, además, servirle no solo de ejemplo para elaborar otras, de acuerdo al contenido que imparta, sino también para diagnosticar el desarrollo de competencias matemáticas en sus estudiantes.
Desarrollo
Actividad 1. Determinando la talla de calzado
Nivel: Problematización
La siguiente tabla muestra las tallas de zapato recomendadas para las diferentes medidas del pie (Tabla 1).
Tabla 1 Tallas de zapato.
| Desde (cm) | Hasta (cm) | Talla |
|---|---|---|
| 10,7 | 11,5 | 18 |
| 11,6 | 12,2 | 19 |
| 12,3 | 12,8 | 20 |
| 12,9 | 13,4 | 21 |
| 13,5 | 13,9 | 22 |
| 4,0 | 14,6 | 23 |
| 14,7 | 15,2 | 24 |
| 15,3 | 15,9 | 25 |
| 16.0 | 16,6 | 26 |
| 16.7 | 17,2 | 27 |
| 17,3 | 17,9 | 28 |
| 18,0 | 18,6 | 29 |
| 18,7 | 19,2 | 30 |
Pregunta 1
El pie de Adriana mide 16,3 cm de longitud. Utiliza la tabla para determinar cuál es la talla de zapatos que debería probarse.
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 26
Sin calificación: para otras respuestas o sin respuesta
La idea principal es que el estudiante establezca relaciones. La operación es de tipo reproductivo, en una situación del contexto personal.
Actividad 2. Chateando con mi amigo en el exterior
Nivel: Problematización
Marco vive en Bogotá y Harold, su gran amigo, se fue a vivir a Dubái, pero a pesar de ello se comunican a menudo a través del chat, y para eso, ambos tienen que conectarse a Internet simultáneamente. Para encontrar una hora apropiada para chatear, Marco buscó un mapa con el horario mundial y halló lo siguiente (Figura 1):
Pregunta 1
Cuando son las 7:00 de la tarde en Bogotá, ¿qué hora es en Dubái?
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 10 o 10 de mañana.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante establezca relaciones. La operación es de tipo conectivo, en una situación del contexto personal.
Pregunta 2
Marco y Harold no pueden chatear entre las 9:00 de la mañana y las 4:30 de la tarde, de sus respectivas horas locales, porque tienen que ir al colegio. Tampoco pueden desde las 11:00 de la noche hasta las 7:00 de la mañana, de sus respectivas horas locales, porque estarán durmiendo.
¿A qué horas podrían chatear Marco y Harold? Escribe las respectivas horas locales en la tabla (Tabla 2).
Calificación máxima: Cualquier hora o intervalo de tiempo que satisfaga las 9 horas de diferencia y que se encuentre dentro de uno de estos intervalos:
Bogotá: 4:30- 6:00 de la tarde; Dubái: 7:30- 9:00 de la mañana,
Bogotá: 7:00 - 8:00 de la mañana; Dubái: 10:00 - 11:00 de la noche
Bogotá 17:00, Dubái 8:00.
Si no se especifica por la mañana (AM) o por la tarde (PM), pero las horas se considerarán de otro modo como correctas, debe darse el beneficio de la duda a la respuesta y considerarla como correcta.
Sin calificación: sin respuesta o para otras respuestas incluyendo una de las dos horas correctas, pero la otra incorrecta.
La idea principal es que el estudiante establezca relaciones. La operación es de tipo reflexivo, en una situación del contexto personal.
Actividad 3. Hallando la altura de los peldaños de la escalera
Nivel: Problematización
El esquema siguiente ilustra una escalera con 14 peldaños y una altura total de 224 cm (Figura 2):
Pregunta 1
¿Cuál es altura de cada uno de los 14 peldaños?
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 16 cm
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante establezca relaciones. La operación es de tipo reproductivo, en una situación del contexto laboral.
Actividad 4. Comprando Pizza
Nivel: Problematización
Una pizzería sirve dos pizzas redondas del mismo grosor y de diferente tamaño. La más pequeña tiene un diámetro de 30 cm y cuesta $30.000. La mayor tiene un diámetro de 40 cm y cuesta $40.000.
Pregunta 1
¿Qué pizza tiene mejor precio?
Muestra tu razonamiento.
Respuesta: ____________________________________________________________
Calificación máxima: Para respuestas que se basan en el razonamiento general de que el área de la superficie de la pizza aumenta más rápidamente que el precio de la misma, concluyendo que la mayor es la mejor compra. Por ejemplo:
El diámetro de las pizzas coincide con su precio, pero la cantidad de pizza obtenida es proporcional al cuadrado del diámetro, por tanto la mayor proporciona más cantidad de pizza por pesos.
Respuestas que calculan el área y la cantidad por peso para cada pizza, concluyendo que la pizza mayor es la mejor compra. Por ejemplo:
El área de la pizza pequeña es Pi x 15 x 15 = 225Pi; la cantidad de pesos por cm2 es de $533. El área de la pizza grande Pi x 20 x 20= 400Pi la cantidad de pesos por cm2 es de $400. Por tanto la pizza mayor tiene mejor precio
Sin calificación: sin respuesta o para otras respuestas:
Respuestas que son correctas pero con un razonamiento incorrecto o insuficiente. Por ejemplo:
Otras respuestas incorrectas.
La idea principal es que el estudiante explore la capacidad para relacionar el tamaño de una figura con su forma. La operación es de tipo conectivo e integradora, en una situación del contexto personal.
Actividad 1. Elaborando repisas
Nivel: Experimentación
Para construir una repisa, un carpintero necesita lo siguiente:
4 tablas largas de madera,
6 tablas cortas de madera,
12 ganchos pequeños,
2 ganchos grandes,
14 tornillos.
Pregunta 1
El carpintero tiene en el almacén 26 tablas largas de madera, 33 tablas cortas de madera, 200 ganchos pequeños, 20 ganchos grandes y 510 tornillos.
¿Cuántas repisas completas puede construir este carpintero?
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 5 estanterías.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante maneje el concepto de cantidad. La operación es de tipo conectivo, en una situación del contexto laboral.
Actividad 2. Hogares con televisión por cable
Nivel: Experimentación
La siguiente tabla muestra los datos correspondientes a los hogares con televisión (TV) en cinco ciudades de Colombia (Tabla 3).
Tabla 3 Hogares con televisión (TV).
| Ciudad | Número de hogares que tienen TV | Porcentaje de hogares con TV con respecto a todos los hogares |
|---|---|---|
| Bogotá | 18,0 millones | 99,8% |
| Barranquilla | 14,5 millones | 15,4% |
| Santa Marta | 4,4 millones | 99,0% |
| Cali | 2,8 millones | 85,8% |
Pregunta 1 La tabla muestra que en Cali el 85,8% de todos los hogares tienen televisión.
Según la información de la tabla, ¿cuál es el cálculo más aproximado del número total de hogares en Cali?
Calificación máxima: si la respuesta es 3,3 millones.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique el concepto de proporcionalidad, a partir de una serie de datos. La operación es de tipo interpretativo, en una situación del contexto social.
Actividad 3. Determinando el costo de cada piso del edificio.
Nivel: Experimentación
Los habitantes de un edificio de pisos deciden comprarlo, por lo cual pondrán el dinero entre todos de modo que cada uno pague una cantidad proporcional al tamaño de su piso.
Por ejemplo, una persona que viva en un piso que mida la cuarta parte de la superficie total de todos los pisos, deberá pagar la cuarta parte del precio total del edificio.
Pregunta 1
Para cada una de las siguientes afirmaciones, determine marcando una equis sobre la palabra Correcto o Incorrecto (Tabla 4).
Tabla 4 Afirmaciones.
| Afirmación | ||
|---|---|---|
| La persona que vive en el piso más grande pagará más dinero por cada metro cuadrado de su piso que la persona que vive en el piso más pequeño. | Correcto | Incorrecto |
| Si se conocen las superficies de dos pisos y el precio de uno de ellos, entonces se puede calcular el precio del otro. | Correcto | Incorrecto |
| Si se conoce el precio del edificio y cuánto pagará cada propietario, entonces se puede calcular la superficie total de todos los pisos | Correcto | Incorrecto |
| Si el precio total del edificio se redujera en un 10%, cada uno de los propietarios pagaría un 10% menos. | Correcto | Incorrecto |
Calificación máxima: si la respuesta es Incorrecto, Correcto, Incorrecto, Correcto, en este orden.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique el concepto de repartos proporcionales. La operación es de tipo conectivo e integrador para la resolución de problemas interpretativo, en una situación del contexto público.
Pregunta 2
Hay tres pisos en el edificio. El mayor de ellos, el piso 1, tiene una superficie total de 100 m2. Los pisos 2 y 3 tienen superficies de 90 m2 y 80 m2, respectivamente. El precio de venta del edificio es de $300.000.000.
¿Cuánto deberá pagar el propietario del piso 2?
Muestra tus cálculos.
Calificación máxima: Para cualquiera de las siguientes respuestas.
$100.000.000 con o sin cálculos.
90/270 x 300.000,000 = $100.000.000
300.000.000/270 x 90= $100.000.000
Puede valorar si utiliza un método correcto, con errores menores de cálculo, como por ejemplo:
90/270 x 300.000.00 = $100.000.000
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique el concepto de repartos proporcionales. La operación es de tipo conectivo e integrador para la resolución de problemas interpretativo, en una situación del contexto público
Actividad 4. Copiando música en mi memoria USB
Nivel: Experimentación
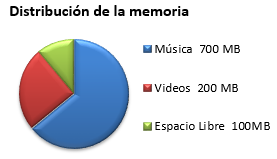
Una memoria USB es un dispositivo pequeño y portátil de almacenamiento de datos informáticos. Carlos tiene una memoria USB en la que almacena música y fotos, que tiene una capacidad de 1 GB (1000 MB). El siguiente gráfico muestra la distribución actual del disco de su memoria USB (Figura 3).
Pregunta 1
Carlos quiere pasar un álbum de fotos de 350 MB a su memoria USB, pero no hay suficiente espacio disponible. Si bien no quiere eliminar ninguna de las fotos, no le importaría eliminar hasta dos álbumes de música. El tamaño de los álbumes de fotos que Carlos tiene almacenados en su memoria USB es el siguiente:
Álbum Tamaño
Álbum 1 100 MB
Álbum 2 75 MB
Álbum 3 80 MB
Álbum 4 55 MB
Álbum 5 60 MB
Álbum 6 80 MB
Álbum 7 75 MB
Álbum 8 125 MB
Álbum 9 50 MB
Eliminando dos álbumes de música como máximo, ¿tendría Carlos suficiente espacio en su memoria USB para añadir el álbum de fotos? Marca una equis sobre la palabra SI o NO. Escribe tus cálculos para justificar tu respuesta.
Respuesta: Sí……………….. No……………………….
Calificación máxima: si la respuesta es SI, y da como ejemplo cualquier combinación de dos álbumes que ocupen 250 MB o más de espacio.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante compare y calcule unos valores para satisfacer los criterios dados. La operación es de tipo interpretativo, en una situación del contexto personal.
Actividad 1. Vamos a diseñar monedas
Nivel: Generalización
Se te pide que diseñes un nuevo conjunto de monedas. Todas serán circulares y de color plateado, pero de diferentes diámetros. Los investigadores han llegado a la conclusión de que un sistema ideal de monedas debe cumplir los requisitos siguientes:
Los diámetros de las monedas no deben ser menores que 10 mm ni ser mayores que 40 mm.
El diámetro de cada moneda debe ser al menos un 25% mayor que el de la anterior.
La maquinaria de acuñar solo puede producir monedas cuyos diámetros estén expresados en un número entero de milímetros (por ejemplo 17 mm es válido, pero 17,3 no).
Pregunta 1
Diseña un conjunto de monedas que satisfaga los requisitos anteriores. Debes empezar con una moneda de 10 mm y el conjunto debe tener el mayor número de monedas posible.
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 10 - 13 - 16 - 20 - 25 -31 - 39. Valore significativamente si representa gráficamente las monedas con los diámetros correctos.
Tenga en cuanta valorar resultados parciales como 10- 13-16- 20.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique un proceso repetido para obtener una solución. La operación es de tipo conectivo e integrador para resolver problemas en una situación del contexto laboral.
Actividad 2. Claudia y su nueva bicicleta
Nivel: Generalización
Claudia acaba de comprar una nueva bicicleta con un velocímetro situado en el manillar.
El velocímetro le indica la distancia que recorre y la velocidad media del trayecto.
Pregunta 1
Durante un trayecto, Claudia hizo 8 km durante los 20 primeros minutos; y luego 4 km durante los 10 minutos siguientes.
¿Cuál de las siguientes afirmaciones es la correcta?
La velocidad media de Claudia fue mayor durante los 20 primeros minutos que durante los 10 minutos siguientes.
La velocidad media de Claudia fue la misma durante los 20 primeros minutos que durante los 10 minutos siguientes.
La velocidad media de Claudia fue menor durante los 20 primeros minutos que durante los 10 minutos siguientes.
No se puede decir nada sobre la velocidad media de Claudia a partir de la información facilitada.
Calificación máxima: si la respuesta es que la velocidad media de Claudia fue la misma durante los 20 primeros minutos que durante los 10 minutos siguientes
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante compare velocidades medias dadas las distancias recorridas y los tiempos empleados y establezca relaciones. La operación es de tipo interpretativo para resolver problemas en una situación del contexto personal.
Pregunta 2
Claudia recorrió 10 km hasta la casa de su tía. El velocímetro marcó una velocidad media de 20 km/h para todo el trayecto.
¿Cuál de las siguientes afirmaciones es la correcta?
A Claudia le llevó 20 minutos llegar a casa de su tía.
A Claudia le llevó 30 minutos llegar a casa de su tía.
A Claudia le llevó 10 minutos llegar a casa de su tía.
No se puede decir cuánto tiempo le llevó a Claudia llegar a casa de su tía.
Muestra tus cálculos.
Calificación máxima: si la respuesta es que a Claudia le llevó 30 minutos llegar a la casa de su tía. Valore si plantea un procedimiento.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante compare velocidades medias dadas las distancias recorridas y los tiempos empleados y establezca relaciones. La operación es de tipo interpretativo para resolver problemas en una situación del contexto personal.
Pregunta 3
Claudia fue en bicicleta desde su casa al río, que está a 6 km. Le llevó 15 minutos. Volvió a casa por una ruta más corta de 4 km, que solo le llevó 9 minutos.
¿Cuál fue la velocidad promedio de Claudia, en km/h, en su trayecto de ida y vuelta al río?
Respuesta: ____________________________________________________________
Muestra tus cálculos.
Calificación máxima: si la respuesta es que la velocidad promedio de Claudia fue de 25.5 halla o no indicado en Km/h.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante calcule la velocidad promedio de dos trayectos dadas las dos distancias recorridas y los tiempos invertidos. La operación es de tipo interpretativo para resolver problemas en una situación del contexto personal.
Actividad 1. Imagen favorable del presidente
Nivel: Generalización
Hace poco, se llevaron a cabo las elecciones de presidente en Colombia, siendo el ganador el Candidato Iván Duque. Los canales de televisión han hecho un sondeo para conocer el nivel de aceptación al presidente. Cuatro canales hicieron sondeos por separado en todo el país. Los resultados de los sondeos de los cuatro canales se muestran a continuación:
Canal Caracol: 36,5% (sondeo realizado el 6 de octubre, con una muestra de 500 ciudadanos elegidos al azar y con derecho a voto).
Canal RCN: 41,0% (sondeo realizado el 20 de octubre, con una muestra de 500 ciudadanos elegidos al azar y con derecho a voto).
Canal Capital: 39,0% (sondeo realizado el 20 de octubre, con una muestra de 1.000 ciudadanos elegidos al azar y con derecho a voto).
Canal UNO: 44,5% (sondeo realizado el 20 de octubre, con 1.000 televidentes que llamaron por teléfono para votar).
Pregunta 1
¿Cuál de los resultados de los canales de televisión sería la mejor predicción del nivel de aceptación al presidente? Da dos razones que justifiquen tu respuesta.
Calificación máxima: si la respuesta es el Canal Capital, ya que el sondeo es más reciente, con una muestra más grande, una selección al azar de la muestra, y sólo se preguntó a votantes. En las dos razones se debe ignorar cualquier información adicional incluyendo información irrelevante o incorrecta. Puede ser:
Canal Capital porque han seleccionado más ciudadanos al azar entre los que tienen derecho a voto.
Canal Capital porque ha pedido la opinión a 1.000 personas seleccionadas al azar, y la fecha es más próxima a la fecha de publicación, por lo que los votantes tienen menos tiempo de cambiar de opinión.
Canal Capital porque fueron seleccionados al azar y tenían derecho a voto.
Canal Capital porque encuestó a más personas y más cerca de la fecha.
Canal Capital porque las 1.000 personas fueron seleccionadas al azar.
Sin calificación: sin respuesta o para otras respuestas como:
Canal Uno porque más personas significa resultados más precisos, y las personas que telefonean habrán considerado mejor sus votos.
La idea principal es que el estudiante maneje la incertidumbre. La operación es de tipo interpretativo, mediante el establecimiento de conexiones, en una situación del contexto social.
Actividad 2. Paseando en bicicleta
Nivel: Generalización
Daniel, Sandra y Carlos montan en bicicletas de tamaños diferentes. La tabla siguiente muestra la distancia recorrida por sus bicicletas por cada vuelta completa de las ruedas (Tabla 5).
Tabla 5 Distancia recorrida por sus bicicletas.
| Distancia recorrida en m | ||||||
|---|---|---|---|---|---|---|
| 1 vuelta | 2 vueltas | 3 vueltas | 4 vueltas | 5 vueltas | ||
| Daniel | 0,96 | 0,92 | 2,88 | 3,84 | 4,80 | |
| Sandra | 1,60 | 3,20 | 4,80 | 6,40 | 8,00 | |
| Carlos | 1,90 | 3,80 | 5,70 | 7,60 | 9,50 | |
Pregunta 1
Carlos impulsó su bicicleta para que las ruedas girasen tres vueltas completas. Si Daniel hiciera lo mismo con la suya, ¿cuántos centímetros más recorrería la bicicleta de Daniel que la de Carlos?
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 2,82 o 2,82 metros.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique el concepto de proporcionalidad, a partir de una serie de datos. La operación es de tipo interpretativo, mediante el establecimiento de conexiones, en una situación del contexto personal.
Pregunta 2
Para que la bicicleta de Sandra recorra 12,80 m, ¿cuántas vueltas tienen que dar sus ruedas?
Respuesta: ____________________________________________________________
Calificación máxima: si la respuesta es 8 vueltas.
Sin calificación: para otras respuestas o sin respuesta.
La idea principal es que el estudiante aplique el concepto de proporcionalidad, a partir de una serie de datos. La operación es de tipo interpretativo, mediante el establecimiento de conexiones, en una situación del contexto personal.
Pregunta 3
La circunferencia de la rueda de la bicicleta de Carlos mide 96 cm (ó 0,96 m). Es una bicicleta de tres marchas con un piñón pequeño, uno mediano y uno grande. Las relaciones de transmisión de la bicicleta de Carlos son:
Piñón pequeño 3:1 (lo que significa que por cada 3 vueltas completas del pedal, cada rueda da 1 vuelta completa)
Piñón mediano 6:5 (lo que significa que por cada 6 vueltas completas del pedal, cada rueda da 5 vueltas completas)
Piñón grande 1:2 (lo que significa que por cada 1 vuelta completas del pedal, cada rueda da 2 vueltas completas)
¿Cuántas vueltas de pedal tendría que dar Carlos para recorrer 960 m con el piñón mediano? Escribe tus cálculos.
Calificación máxima: si la respuesta es 1200 vueltas de pedal, sustentado en el siguiente procedimiento:
960 m requieren 1000 vueltas de la rueda, que corresponden a 1000 x 6/5=1200 vueltas de pedal.
La calificación máxima puede variar si calcula por un método correcto pero se equivoca al convertir las unidades o comete un ligero error de cálculo:
960 m requieren 10 vueltas de rueda que corresponde a 10 x 6/5=12 vueltas de pedal
3 vueltas de pedal producen 2,5 vueltas de rueda, y una vuelta de rueda = 0,96 m, por tanto 3 vueltas de pedal = 2,4 m. En consecuencia, 960 m requieren 400 vueltas de pedal.
Hacen falta 1000 vueltas de rueda (960/0,96) para avanzar 960 m, de modo que se necesitan 833 vueltas de pedal con el piñón mediano (5/6 de 1000).
5 x 0,96 =4,8, y 960/4,8 = 200, de modo que 200 vueltas. Ahora 200/5 = 40 y 40 x 6 =240. De modo que se necesitan 240 vueltas de pedal.
Sin calificación: sin respuesta o para otras respuestas como:
96.000/5 = 19.200, y 19.200 x 6 =115.200 vueltas de pedal, donde se ve que no tuvo en cuenta la circunferencia de la rueda.
La idea principal es que el estudiante aplique el concepto de proporcionalidad, a partir de una serie de datos. La operación es de tipo interpretativo, mediante el establecimiento de conexiones, en una situación del contexto personal.
Conclusiones
Como resultado de la aplicación de la cartilla de ejercicios, se plantean las siguientes conclusiones.
Las actividades que se proponen demuestran como la matemática puede ser utilizada directamente o indirectamente en situaciones de la cotidianidad.
Las respuestas de los estudiantes deben ser consideradas con base a los planteamientos y procedimientos que desarrollen.