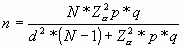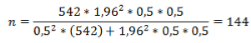Introducción
La resolución de los problemas matemáticos es un tema de estudio desarrollado por varios autores, debido al desafío que supone que los estudiantes lean y comprendan los elementos que los conforman, identifiquen la pregunta que necesita ser respondida y puedan seguir el algoritmo correspondiente. El origen de esta situación puede deberse a que desde las edades tempranas se les enseña a los estudiantes la resolución de problemas de forma repetitiva y mecánica, trabajar con informaciones que no se ajustan a la edad de los niños, escasa conexión entre el abordaje de la matemática y situaciones de vida de los discentes, como consecuencia se tiene que los estudiantes en forma mecánica resuelven los problemas generando rechazo para el aprendizaje de la matemática.
Pero es evidente, lo planteado por Barrientos (2017), al comprenderse que en los procesos matemáticos, la gran mayoría de los estudiantes tienen problemas, especialmente aquellos que no desarrollan la comprensión lectora, por lo que el estudiante no está en la capacidad de procesar, analizar, deducir y construir, aprendizajes a partir de textos que estén relacionados con problemas matemáticos. Según Polya (1989), citado en Blanco & Cárdenaz (2013) para "resolver un problema matemático primero se tiene que entender el problema, desarrollar un plan, ejecutar el plan y comprobarlo". (p. 23)
Por lo que, se ha de destacar que estas dos variables se encuentran altamente relacionadas tal como lo corroboran las investigaciones que al respecto se han llevado a cabo por Varillas & Zarzosa (2015); Cárdenas, et al., (2018); Canales (2018). Estos autores encontraron que la comprensión lectora y la capacidad de resolución de problemas matemáticos se relacionan significativamente, destacando que, a un mayor nivel de comprensión lectora, mayor será la capacidad del estudiante para plantear y resolver problemas matemáticos. Asimismo, determinaron que existe una relación directa y muy significativa entre el nivel literal, inferencial y la resolución de problemas matemáticos, con la comprensión lectora. De tal manera, que la primera dificultad que los estudiantes enfrentan al tratar de resolver un problema matemático es intentar comprender lo planteado, por lo que la lectura sin comprensión e interpretación resulta insuficiente y más aún cuando se trata de resolver un problema.
En el caso de Ecuador, según el estudio PISA-D (Ecuador. Instituto Nacional de Evaluación Educativa, 2018), solo el 14% de la población estudiantil egresado del nivel educativo medio, demuestran un nivel satisfactorio en comprensión lectora para la resolución de problemas, estas cifras indican las posibles causas de que los estudiantes no concreten el procedimiento para la resolución de problemas. Esta problemática se presenta en los estudiantes de nivel medio en la institución educativa ecuatoriana, lo cual hace plantearse la siguiente interrogante: ¿La comprensión lectora influye en la ejecución del plan de resolución de los problemas matemáticos de los estudiantes de la Unidad Educativa San Alfonso?
Desarrollo
Es necesario tener una comprensión de lo que significa un Problema Matemático. En este sentido, se define como aquel problema que es susceptible de ser representado, analizado y resuelto a través de métodos matemáticos al resolver el problema este se demuestra formalmente. Este es el núcleo del análisis, se plantea en torno a preguntas que busquen una respuesta, a partir de la exploración se logra el aprendizaje por procesos, bien sea individual o grupal, además que permite comunicar los resultados. El problema debe estar planteado en torno a preguntas e interrogantes que busquen una respuesta desde la exploración, ya que ello permitirá alcanzar un aprendizaje de procesos mediante el trabajo individual, grupal y la comunicación de los resultados (Rodríguez, et al., 2017).
La comprensión del problema matemático requiere de un proceso de evaluación y el desarrollo de instrumentos, teniendo que considerar elementos como: la comprensión y expresión; la capacidad de identificación, resolución de problemas y el razonamiento a partir del cual se identifique el procedimiento requerido. Durante este proceso el estudiante es capaz de representar gráficamente, expresar un concepto, sistematizar, y resumir conclusiones. Esto le permitirá interpretar las ideas matemáticas, traducir los elementos de una expresión a otra y argumentar las estrategias más oportunas. En el proceso de evaluación se tendrá en cuenta la organización del procedimiento, los procesos de síntesis, el planteamiento y resolución del problema.
La comprensión lectora se relaciona con aquellos procesos que involucran la resolución de problemas, el conocimiento de la matemática y las competencias en los estudiantes (Carreira, 2013). También se observa en el estudiantado la falta de confianza y fallas en la resolución del problema, delegar en otros la resolución de los problemas, falta de conexión activa entre los conocimientos previos y lo que aprenden en el momento, escasas estrategias de resolución y poca solicitud de ayuda de estudiantes que comprenden problemas matemáticos. Otro aspecto es los problemas de memoria en aquellos casos en que los estudiantes tienen dificultad para recordar operaciones básicas, o en aquellos casos que se requiere pasos específicos para la resolución de problemas y no acuden a su aprendizaje previo.
La Heurística en educación matemática, facilita la resolución de problemas, siendo una estrategia que se utiliza para encontrar la solución a los problemas. Dentro de las corrientes teóricas la propuesta Polya (1989), sigue estando presente en el contexto actual. Para ello, se conceptualiza un plan para la resolución del problema previamente elaborando un método para llegar a la respuesta de lo requerido en los cálculos próximos y sucesivos. De lo cual emerge una estrategia para la resolución basada en criterios como la plausibilidad, rapidez y la familiarización o experiencia, tiempo, recursos con los que se cuenta para la resolución que es la base conceptual y las herramientas metodológicas logrando tener éxito si se tiene dominio en los conocimientos (Minotta, 2014).
El problema matemático
Por tanto, un problema es una nueva situación que presenta una serie de dificultades para obtener una solución y tiene como objetivo descubrir el camino para obtener un resultado de la manera más adecuada y exacta posible. Debido a que está constituido por datos, objetivos y obstáculos; por lo que su resolución exitosa dependerá de estrategias, intereses, motivaciones y conciencia del problema. La mayoría de estos problemas se utilizan para ejercer la resolución de operaciones y como una herramienta para alentar y facilitar las tareas de la vida diaria utilizando las matemáticas, en otras palabras, propone al estudiante una situación (de preferencia conocida) o una declaración que propone un obstáculo que debe superarse utilizando las operaciones matemáticas correspondientes.
La comprensión del texto del problema
La comprensión del texto del problema, es un acto de razonamiento, ya que de lo que se trata es de saber guiar una serie de acciones lógicas hacia la construcción de una interpretación de lo escrito en el texto y los conocimientos del lector y, a la vez, iniciar otra serie de razonamientos para controlar el progreso de esa interpretación de tal forma que se puedan detectar las posibles incomprensiones producidas durante la lectura del texto del problema (Otero, Papini & Elichiribehety, 2016).
Según este mismo autor, la comprensión del problema es esencial para su solución exitosa, para lo cual el lector debe preguntarse: ¿Qué es lo que se busca? ¿Qué se desea saber? y discriminar los datos con los que se cuenta en la búsqueda de la solución. Este proceso es complejo, y contiene cuatro aspectos indispensables que permite desarrollar diferentes habilidades como: analizar (formarse una opinión, sacar ideas centrales, deducir y predecir conclusiones); retener (conceptos fundamentales, datos para responder a la preguntas, detalles aislados, detalles coordinados); organizar (establecer consecuencias, esquematizar, resumir y generalizar) y valorar (comprender el sentido de lo leído, formar relaciones causa-efecto, diferenciar hechos de las opiniones, distinguir lo verdadero de lo falso y lo real de lo imaginario).
Niveles de comprensión lectora
El proceso de comprensión se clasificarse en tres niveles, según Benítez, Espinoza & Pérez (2015):
Nivel Literal: Se clasifica en dos niveles, se centraliza en las ideas e información que están explícitamente presentadas en el texto, por reconocimiento o evocación de hechos. También se identifica el tema principal, realizando síntesis y resúmenes.
Nivel Inferencial: El objetivo de este nivel será la elaboración de conclusiones. Este nivel de comprensión es poco puesto en práctica en las instituciones, ya que necesita un considerable nivel de abstracción.
Nivel Crítico: Se realizan juicios sobre lo leído, se rechaza o se acepta, pero con fundamentos. La lectura crítica es evaluativa donde participa la formación del lector, sus conocimientos y criterio de lo leído.
Resolución de un problema matemático
Para resolver un problema, lo primero que debe hacer el estudiante es leerlo, lo cual implica realizar la comprensión lectora necesaria, misma que se define como “la capacidad para producir conocimiento a partir de la lectura; no se trata sólo de entender qué se dice, sino crear más información, misma que el sujeto interpreta, infiere y recrea a partir de lo que ha leído”. En este orden de los planteamientos, la capacidad lectora se relaciona con la resolución del problema, ya que en la medida en la que el estudiante comprende el problema leído tiene herramientas y técnicas para su resolución.
El plan de resolución
En la resolución de un problema según el modelo de Polya (1989), se debe realizar a través de cuatro fases:
Comprender el problema: se realiza la lectura del problema y se plantean preguntas relacionadas, tales como: ¿Cuál es la incógnita?, ¿Cuáles son los datos?, ¿Cuál es la condición?, ¿Es posible satisfacer la condición?, en esta pregunta no se espera una respuesta definitiva, sino más bien provisional. En caso de haber alguna figura relacionada con el problema, se debe analizar la figura y destacar en ella la incógnita y los datos. Para ello se procede realizando una lectura comprensiva, interrogar lo que no se comprende, enunciar el problema con las propias palabras, establecer lo que se solicita en la orden y los datos que aporta el problema y seleccionar los datos necesarios para el cálculo.
Concepción de un plan: Polya (1989), explica que se tiene un plan cuando se sabe, en cierto modo, qué cálculos, qué razonamientos o construcciones se efectuarán para determinar la incógnita. Para lo que se escriben los datos relevantes del problema, relacionar con un problema conocido al que se está presentando y tratar de resolverlo, si el problema es muy complejo buscar la manera de simplificarlo y establecer claramente las operaciones matemáticas que se deben aplicar para su resolución.
Ejecución del plan: Al ejecutar el plan se debe comprobar que cada uno de los pasos sea correcto, asegurando el éxito en la resolución del mismo. Sobre lo que se debe realizar los cálculos pertinentes, comparar resultados, y establecer un orden de desarrollo del problema.
Verificar los resultados: una vez obtenida la solución del problema y expuesto claramente el razonamiento, existe un medio rápido e intuitivo para asegurarse de la exactitud del resultado o del razonamiento, mediante las preguntas: ¿Puede comprobar el resultado? ¿Puede comprobar el razonamiento? ¿Puede obtener la respuesta de un modo distinto? En lo que se procede a verificar los resultados alcanzados para identificar si son parciales o finales, llegar a la solución por diferentes vías, comparar los resultados obtenidos, determinar si cumple con las condiciones del problema y finalmente formular un breve análisis como respuesta.
Principales problemas asociados a la comprensión y al plan
Dentro de las dificultades que se encuentran asociadas a la comprensión lectora, según Chandia, et al. (2016), se mencionan las siguientes:
Dificultades en la lectura: los estudiantes deben haber desarrollado la habilidad de una lectura comprensiva y critica para lograr resolver el problema, esta carencia genera dificultades para la resolución del problema, puesto que, si no lee bien, no comprende la lectura y no puede dar las soluciones adecuadas al problema.
Dificultad para entender frases y conceptos matemáticos: los problemas matemáticos presentan ciertas “pistas”, que los estudiantes deben descifrar para resolver el problema es lo que se conoce como oraciones numéricas, sobre las cuales el individuo puede imaginarse esta oración numérica y otros para llegar a comprenderla deben escribirla, pero entre determinar estas pistas y la resolución del problema, existen pasos adicionales que deben seguirse adecuadamente.
Dificultad con la atención y el autocontrol: los estudiantes pueden leer el problema y explicar cómo se resuelve, pero pueden dar una respuesta equivocada, debido a la poca atención y autocontrol, llegando a distraerse con las palabras y otras ideas que extraen del problema, lo que los conlleva a omitir partes importantes o cometer errores de cálculo simple; otro aspecto que se debe considerar es que en algunos problema se incorpora información adicional que no es necesaria para resolver el problema y solo crea confusiones
Metodología
La investigación se encuentra dentro del enfoque cuantitativo, descriptivo y transversal dado que el análisis de las variables se realizará a través del uso de herramientas estadísticas y la interpretación por parte del investigador del fenómeno observado, las dos variables implícitas en el estudio son, la comprensión y resolución de problemas matemáticos las cuales serán analizadas de manera independiente y luego se realizarán correlaciones para comprobar o desechar si alguna de las variables tiene incidencia en la otra utilizando procedimientos estadísticos, cuyos datos fueron recogidos en el campo en un único momento (Hernández, Fernández & Batista, 2014; Lerma, 2016).
La técnica de investigación fue la encuesta siendo el instrumento ACL 6 con el cual se evaluó la comprensión lectora de problemas de matemática y una prueba de conocimiento matemático que incluyó preguntas siguiendo los pasos en la ejecución del plan de resolución. En relación al instrumento ACL-6, este consta de 10 textos en un total de 36 preguntas. Con referencia a los textos de este instrumento, se ha tenido en cuenta de manera respetuosa la tipología textual planteada por los creadores de la prueba.
Cada uno de los textos tiene un subconjunto de palabras específicas de su manejo cotidiano antes de responder la lectura de “diferentes tipologías textuales: narrativos, expositivos, retóricos que afectan diferentes áreas curriculares, lengua y literatura, matemática, medio social y medio natural” (Catalá et al. (2001, p.34).
Se buscó que los textos tengan claridad de expresión, evitando adiciones falsas y aislado, tratando de estructurar textos que son breves en su expresión, sin pasar por construcciones gramaticales extensas. Los ítems solo se refieren a una idea central y las preguntas, en su mayor parte, se presentan en una estructura positiva con respecto al orden de los textos y elementos. Sobre las respuestas múltiples la correcta fue dispersada en diferentes posiciones, longitud y manera en la que se expuso, sin llegar a ser evidentes.
Para su aplicación, se implementa el folleto de los textos, lápiz, borrador y hojas de respuestas, el cual se aplica en un tiempo aproximado de 60 minutos. Se pide a los estudiantes que lo lean individualmente y en silencio, a continuación, el docente lo lee en voz alta, de manera expresiva, después de dejar un espacio de tiempo para que piensen cuál es la opción correcta, se pide a algún alumno que responda cual ha elegido y que razones por qué, enseguida se contrasta la respuesta con la dada por los demás, luego se sigue igual con las otras preguntas del ejemplo, comentando específicamente esos aspectos que pueden ser conflictivos.
Corrección y valoración de los resultados: para la corrección de la prueba, el docente procede a comparar las respuestas dadas con la tabla de respuestas correctas, para cada respuesta correcta le dará un punto, si el estudiante ha marcado dos o más alternativas, no ha dejado ninguna pregunta sin responder, en la puntuación de ese ítem será cero, finalmente la suma de todas las respuestas, el éxito dará una puntuación total de 36 puntos.
Escala de valoración: una vez aplicado el instrumento sobre comprensión lectora, elabora el baremo por medio de la escala de rango. Que a continuación se muestra en la tabla, en el que se observa en cada una de las dimensiones aplicadas y los resultados finales con sus intervalos de puntuación y su respectiva interpretación (Tabla 1).
Tabla 1 - Rangos de los niveles de comprensión lectora.
| Rangos | Comprensión literal | Comprensión reorganización | Comprensión inferencial | Comprensión crítica | Comprensión lectora |
| 1 | 0 - 4 | 0 - 3 | 0 - 3 | 0 - 1 | 0 - 11 |
| 2 | 5 - 6 | 4 - 5 | 4 - 6 | 1 - 2 | 12 - 17 |
| 3 | 7 - 9 | 6 - 7 | 7 - 9 | 2 - 3 | 18 - 28 |
| Rangos | - | Interpretación | - | - | - |
| 1 | - | Nivel bajo | - | - | - |
| 2 | - | Nivel medio | - | - | - |
| 3 | - | Nivel alto | - | - | - |
Fuente: Catalá, et al. (2001).
Clasificación textual, preguntas y alternativas correctas.
En la siguiente tabla se presenta los textos que comprenden el instrumento sobre comprensión de lectura, con su tipología textual, el número de preguntas y sus alternativas de respuesta (Tabla 2).
Tabla 2 - Tipología textual, preguntas y alternativas.
| Tipología textual | Texto | Preguntas | Alternativa correcta |
| Narrativo | 1. Un pobre | 1, 2, 3, 4 | E, B, A, D |
| Expositivo | 2. Cuando llega el invierno | 5, 6 | B, D |
| Poético | 3. Pierrot | 7, 8, 9, 10 | C, D, D, C |
| Interpretación de gráficos | 4. Mensajes | 11, 12, 13, 14 | E, C, E, C |
| Narrativo | 5. Discurso del jefe indio | 15, 16, 17, 18 | E, A, E, D |
| Narrativo | 6. La dama | 19, 20, 21, 22 | A, C, B, D |
| Interpretación de gráficos | 7. Mar | 23, 24, 25, 26, 27 | E, D, C, A, C |
| Expositivo | 8. Empresas | 28, 29, 30 | B, D, D |
| Interpretación de gráficos | 9. Restaurantes | 31, 32, 33 | D, B,D |
| Expositivo | 10. Cuando llega el invierno | 34, 35, 36 | B, E, A |
En cuanto al instrumento aplicado para evaluar el conocimiento matemático se diseñó con 5 preguntas donde se plantearon problemas para su resolución y adicionalmente responder a ciertas preguntas que permiten evidenciar el nivel resolutivo acerca del planteamiento, ejecución y resultado que se le debe dar al problema planteado. Adicionalmente responder a:
¿Cuál es la incógnita del problema?
¿Qué datos tiene para resolver el problema?
¿Qué operaciones se deben realizar para resolver del problema?
¿Cuál es el orden de las operaciones para resolver el problema?
¿Cuál es la respuesta del problema?
¿Cómo compruebo que mi respuesta es correcta?
La población estuvo conformada por 542 estudiantes de la Unidad Educativa San Alfonso. Para la selección de la muestra se aplicó la siguiente formula:
Donde:
N = |
Total de la población 542 |
Za 2= |
1.962(si la seguridad es del 95%) |
p = |
proporción esperada (en este caso 5% = 0.5) |
q = |
1 - p (en este caso 1-0.5 = 0.5) |
d = |
precisión (en este caso deseamos un 5%) |
Se procedió a trabajar con una muestra de tipo probabilística constituida por 144 estudiantes del quinto, sexto y séptimo de primaria, seleccionados de forma probabilística al azar, a quienes se les aplicó el instrumento, fueron elegidos estos cursos por las características de que podían responder la prueba y arrojar resultados objetivos y confiables, con lo cual fue posible evaluar el nivel de respuesta de los estudiantes y su comprensión del problema matemático. Adicionalmente se utilizó una escala de estimación, en el cual el docente registró las observaciones y respuestas dadas por los estudiantes. Dichos datos fueron procesados mediante el programa SPSS versión 25 representando las frecuencias y porcentajes para su respectivo análisis, estableciendo la relación entre las variables y comprobando la hipótesis propuesta.
Resultados
Descripción de la comprensión lectora y la resolución de problemas matemáticos
Resultados de la aplicación del instrumento para valorar la comprensión lectora
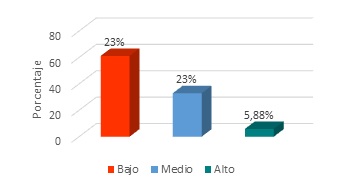
Dimensión: Comprensión lectora Gráfico 1
Según los resultados de la figura 1, respecto a la Dimensión: Comprensión lectora, el 32,94% se encontró en el nivel bajo, el 23 % de la muestra se ubicó en el nivel medio y el 5,88% se encontró en el nivel alto. Se evidenció que un alto porcentaje (55,94%) de los estudiantes presentan problemas en la comprensión lectora, lo que le dificulta entender y discernir los problemas matemáticos y así mismo la aplicación de un plan de resolución del ejercicio.
Estos resultados coinciden con los obtenidos por estudios como el de Pérez & Hernández (2015), quienes sostienen que los estudiantes presentaban dificultad de leer el contenido del texto, ya que no llegan a comprender lo que leen, que en base a una mejora en la comprensión del planteamiento la relación con la resolución de problemas debe afianzarse sustancialmente, demostrando que la variable comprensión del problema matemático es básico, para que los alumnos entiendan el enunciado del problema matemático y puedan proceder a su ejecución.
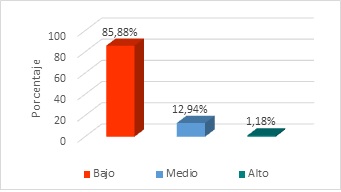
Dimensión: Literal (Figura 2).
En la Figura 2, se tiene que el 85,88% de los alumnos se encuentran dentro de la dimensión literal en un nivel bajo, el 12,94% en el nivel medio y solo el 1,18% se ubicó en el nivel alto. De lo que se deriva que un alto porcentaje (98,82%) de los estudiantes se encuentran entre el nivel bajo y medio en el proceso de realizar inferencias en la resolución de los problemas matemáticos. Esto demuestra que los estudiantes en relación a la lectura presentaron grandes dificultades para interactuar con el texto, con poca capacidad para decodificar la información e interpretar los componentes de un texto, y la memoria no está activada a corto y largo plazo para el almacenamiento de información.
Dimensión: Reorganizacional (Figura 3)
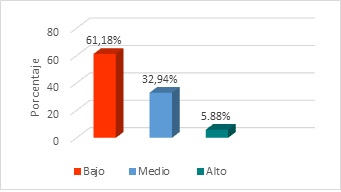
En la figura 3 se muestra que el 61,18% de los estudiantes se encuentra en un nivel bajo en el rendimiento lector según la dimensión reorganizacional, el 32,94% se ubicó en el nivel medio y el 5,88% en el nivel alto. Este resultado muestra que más de la mitad de los estudiantes en relación a la función lectora exponen una comprensión limitada del texto, es decir, no hacen un resumen, un acercamiento a la información textual, una síntesis u organizar la información a través de organizadores gráficos.
Estos resultados permiten afirmar que los estudiantes en un porcentaje representativo (94,12%) presentan dificultades al momento de reorganizar la información extraída del texto, al proponérsele actividades que implican desarrollo cognitivo complejo, como: analizar, organizar, comprender entender y evaluar la información suministrada.
Dimensión: Inferencial (Figura 4)
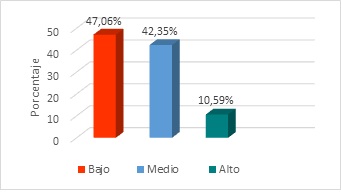
Los resultados expuestos en la Figura 4 muestran que el 47,06% de los estudiantes se encuentra en un nivel bajo en el rendimiento lector según la dimensión inferencial, el 42,35% se ubicó en el nivel medio y solo el 10,59% se encontró en el nivel alto. Sobre lo cual se puede manifestar que el lector no aplica estrategias para el funcionamiento de la intuición y deducción de secuencias, relaciones de causa-efecto con su aprendizaje previo para desarrollar nuevas ideas y lograr construir conjeturas, pronunciar anticipos y elaborar posibles respuestas.
Dimensión: Criterial (Figura 5).
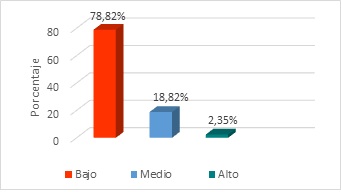
Los resultados que se muestran en el grafico 5, evidencian que el 78,82% de los estudiantes se encuentran en un nivel bajo en el rendimiento lector según la dimensión criterial, el 18,82% se ubicó en el nivel medio y solo el 2,35% se encontró en el nivel alto. De lo cual se obtiene que, si los lectores están a este nivel, es porque presentan grandes dificultades para una evaluación exhaustiva del texto como: juicio evaluativo de hechos u opiniones, diferencia lo ficticio con la realidad, el lector no logra hacer una inferencia que trascienda el contexto donde se desarrolla sin poder cuestionar la nueva información para construir su propio concepto personal (Catalá, 2007).
Resultados de la ejecución del plan de resolución de problemas
Dimensión: Planteamiento (Figura 6).
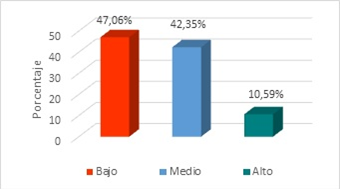
Según los resultados que muestra la Figura 4 el 47,06% de los alumnos se encuentran en el nivel bajo en la comprensión para realizar el planteamiento del problema matemático; mientras que el 42,35% se ubicó en el nivel medio y el 10,59% se encontró en logrado y consolidado. Este resultado evidencia el gran inconveniente que presentan los estudiantes para comprender el planteamiento del problema.
Estos resultados guardan similitud con el estudio de Nieto (2015), cuando afirma que el manejo de números resulta ser históricamente más difícil, lógico y específico que el texto literal, por lo cual estos resultados comparativamente resultan ser congruentes, en el que persiste el bajo rendimiento escolar por lo que continúa siendo un problema a resolver, siendo entre otras causas la forma deficiente que los estudiantes muestran en el dominio de los diferentes niveles de comprensión de contenidos matemático (literal, inferencial, criterial) motivo por el cual no comprenden el planteamiento de un problema matemático y le impide su resolución.
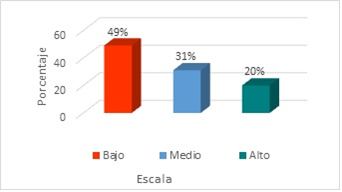
Dimensión: Ejecución (Figura 7).
De la Figura 7 se obtuvo que el 49% de los estudiantes se encuentra en el nivel bajo para la dimensión ejecución del problema, el 31% en el nivel medio y el 20% se ubicó en el nivel alto. De lo que se tiene que los estudiantes en un alto porcentaje presentan dificultades para ejecutar el problema matemático, pues la organización y secuencia del problema para su resolución, no se adecua a un plan que permita una buena ejecución, de forma que puedan lograrse los resultados esperados al llevar a cabo su resolución, detectándose que el plan propuesto no es el más adecuado, implicándose deficiencias en la comprensión del contenido y los datos suministrados en su ejecución.
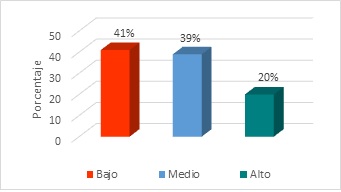
Dimensión: Resultado (Figura 8).
La Figura 8 muestra que el 41% de los estudiantes se ubicó en el nivel bajo, al obtener los resultados al problema matemático planteado; el 39% se encontró en el nivel medio, el restante 20% se ubicó en el nivel alto. Es evidente, según estos resultados que un alto porcentaje de los estudiantes presentaron deficiencias en cuanto a la obtención de los resultados de la ejecución del plan de resolución de problemas.
Tabla 3 Correlación entre la Comprensión del Problema Matemático y la Ejecución del Plan de Resolución. Correlaciones
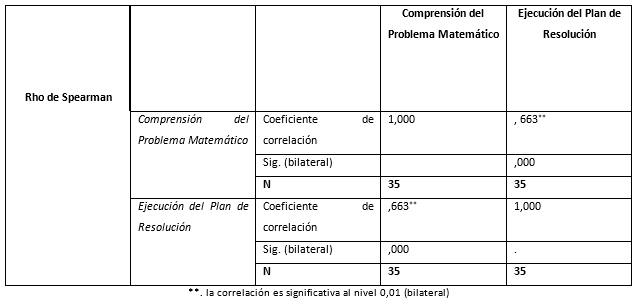
En la Tabla 3 se muestra que la comprensión de los contenidos matemáticos se relaciona significativamente con la ejecución del plan de resolución de problemas, con lo que se acepta la hipótesis, quedando confirmada la correlación, en base a que el valor de Rho de Spearman se encontró en el rango de 0.60-0.80, con lo que se puede afirmar que existe una relación significativa de tipo positivo entre la comprensión de los contenidos matemáticos y la ejecución del plan de resolución del problema.
Estos resultados son corroborados por el estudio realizado por Barrientos (2017), evidencia situaciones interesantes, observadas también en esta investigación, que las hacen comparables en el mismo sentido u orientación y que contribuyen adicionalmente a la falta de comprensión del problema, es que la falta de distinción por algunos docentes entre lo que representa un ejercicio y lo que demuestra un problema les impide encontrar alternativas para resolver los problemas. Ya que, normalmente, un estudiante se siente frustrado y con falta de iniciativa para resolver un problema matemático al no poder encontrar la forma de aplicar un plan de ejecución en su resolución que le facilite proporcionar un resultado objetivo y científico del mismo.
Conclusiones
Los resultados del presente estudio indican, que la comprensión del problema es importante para la ejecución del plan de resolución, puesto que según la teoría de Polya (1989), para llevar a cabo este proceso, en la primera fase se requiere comprender el problema, de la cual se derivan los siguientes procedimientos. El estudio empírico realizado en estudiantes del EGB nivel medio de la Unidad Educativa San Alfonso en Ecuador reveló que, un alto porcentaje (55,94%) presentan problemas en la comprensión lectora, y por consiguiente en la aplicación de un plan de resolución del ejercicio.
Se encontró, que los estudiantes, presentaron dificultades para comprender el contenido del problema matemático, la discriminación de los datos suministrados para su ejecución, establecer relaciones con los datos literales y numéricos. Todo ello evidencia falta de dominio de los procedimientos para conformar un plan de resolución organizado, su ejecución, desarrollo y los resultados obtenidos.
Reportar los resultados del problema matemático, pues también se encontraron dificultades para establecer alternativas para resolverlo, esto repercute en que el estudiante se sienta frustrado y con falta de iniciativa para resolver un problema matemático, lo que les impide ejecutar operaciones matemáticas y obtener el correcto resultado luego de relacionar datos literales y numéricos en la resolución de un problema matemático.
Por tanto, se verificó que la comprensión incide en la ejecución del plan de resolución de problemas matemáticos en los estudiantes de EGB nivel medio de la Unidad Educativa San Alfonso, a partir de una correlación significativamente positiva entre las variables Comprensión del Problema Matemático y la Ejecución del Plan de Resolución de un 0.663.