Introducción
El dominio de los conceptos matemáticos es una parte esencial de la formación matemática de un estudiante. Tales conceptos, según González (2005), constituyen una clase especial y como tales deben ser tratados.
Los conceptos matemáticos son abstractos, por tanto, solo tienen existencia en la mente humana; se forman a partir de objetos o grupos de objetos, reales o pensados, a los cuales se considera desprovistos de contenidos; son siempre genéricos porque se refieren a grupos de objetos que tienen características comunes, de ahí que se puede afirmar que los conceptos matemáticos están estrechamente relacionados con la experiencia y la percepción de las cosas y a veces resulta en algunas aparentes contradicciones.
Para comprender con claridad cómo se puede estructurar, desde el punto de vista didáctico, el proceso de formación de conceptos matemáticos, es necesario tener en cuenta, tres aspectos esenciales: en primer lugar, las etapas de este proceso y los niveles que transita la formación de conceptos en la medida en que se van descubriendo nuevas instancias de él en el transcurso de la enseñanza, en segundo lugar, las vías y los procedimientos que pueden ser utilizados para formar (construir o elaborar) un nuevo concepto y, en tercer lugar, los principios en los cuales se sustenta este proceso.
En este trabajo se exponen los principales resultados de una investigación teórica realizada por los autores sobre estos tres aspectos, donde se sistematizan e integran resultados de investigaciones precedentes sobre la problemática.
Desarrollo
Al referirse a cómo se forman los conceptos González (2005), afirma que un concepto no se forma repentinamente; al contrario, se forma progresivamente y es ampliado y profundizado a medida que son encontradas nuevas instancias de él y son establecidas sus relaciones con otros conceptos del mismo sistema conceptual al cual pertenece.
Esa formación paulatina de los conceptos, según explica este autor, involucra cierta cantidad de ensayo y error mediante la cual se trata de determinar si algún objeto puede ser considerado o no como ejemplo de algunos de los conceptos que ya han sido o están siendo formados. Esta actividad conduce a diversos grados de dominio de los conceptos, desde un nivel prácticamente de no existencia del concepto hasta un nivel elevadamente abstracto, pasando por algunos niveles intermedios.
La afirmación de González, deja entrever que en el proceso de formación de conceptos hay etapas y niveles. Un concepto matemático se puede formar en una determinada etapa, a un cierto nivel y después puede ser ampliado y profundizado en etapas y niveles superiores.
Autores como Ballester, et al. (2002); Curbeira, Bravo & Bravo (2013), refiriéndose al tratamiento metodológico de los conceptos a largo plazo, reconocen que se pueden identificar tres fases, que son:
La primera fase está caracterizada por consideraciones y ejercicios preparatorios.
La segunda fase consiste en la formación del concepto (esta fase está estrechamente relacionada con el objetivo de capacitar al estudiante para definir).
La tercera fase consiste en la asimilación y fijación del concepto.
Los autores de esta investigación reconocen que la fase que estos autores reconocen como formación del concepto es en sí misma un proceso y cómo todo proceso pueden reconocerse en él determinadas etapas o fases, que estos autores no reconocen. Solo se limitan a ofrecer determinados pasos metodológicos para definir formalmente un concepto, utilizando diferentes vías.
Un concepto puede ser adquirido por lo estudiantes en la primera infancia y después seguir perfeccionándose en grados posteriores en la medida en que va avanzando en los estudios.
Si se toma en consideración los tipos de pensamiento que predominan en cada etapa escolar (Majmutov, 1983), así como, el nivel de desarrollo del lenguaje del estudiante (Vigotsky, 1962) y los planteamientos de González (2005), entonces se pueden identificar las fases o etapas de este proceso.
Los autores de esta investigación, sobre la base de lo planteado por Majmutov, reconocen tres etapas fundamentales en el proceso de formación de conceptos matemáticos, que son:
Etapa conceptual - informal: donde predomina el pensamiento en imágenes, es decir, lo que se forma es una imagen del concepto, que es el conjunto de todas las imágenes mentales asociadas en la mente del estudiante con el nombre del concepto, pudiendo tratarse de una representación visual o bien de una serie de impresiones o experiencias Tall & Vinner (1981), la imagen del concepto se forma con ayuda de los adultos, como resultado de las actividades cotidianas que realiza el niño, sin que medie razonamiento alguno. Las imágenes y representaciones mentales del concepto que poseen los niños tienen un papel primario y ellas son evocadas en el momento en que las necesiten.
Esta etapa transcurre en el preescolar y como resultado se forman los llamados conceptos cotidianos o espontáneos como los calificó Vygotsky (1962).
Esta etapa es la base para la formación o construcción de los conceptos en la educación primaria.
Etapa concreto - conceptual: en esta etapa, tal y como lo señala Majmutov (1983), el proceso de formación de los conceptos se realiza a través del paso del pensamiento de imágenes al conceptual, en ella se forman los denominados conceptos empíricos, sobre la base de generalizaciones empíricas, es decir, sobre la base de las características externas, observables de los “objetos matemáticos”, donde los conceptos no se definen, se forman con ayuda de los métodos sustitutos para la definición de conceptos, tales como: comparación, distinción, ejemplificaciones, descripciones y caracterizaciones o la combinación de estas dos últimas.
En esta etapa predomina el razonamiento empírico - inductivo y tiene lugar básicamente en la educación básica primaria, aunque no se excluye la posibilidad y la conveniencia de utilizarlos en menor grado en la educación básica secundaria.
Esta etapa es de suma importancia para la posterior formación de los conceptos abstractos. Al respecto Puig Adam (1960), citado por Rico & Sierra (1994), acota: “así, antes de iniciar el método lógico ha de haberse acumulado en la mente del alumno un rico caudal de observaciones, de experiencias y de intuiciones efectuados desde los primeros años de la escuela y que, sedimentadas en lo inconsciente del niño, sean el germen de los conceptos abstractos”.
Etapa abstracto - conceptual: en esta etapa el proceso de formación de conceptos se efectúa a través del paso del pensamiento concreto - conceptual al abstracto - conceptual (Majmutov, 1983). En ella se definen formalmente los conceptos matemáticos a partir de la identificación de sus atributos relevantes (rasgos esenciales). Se comprende la estructura lógica de una definición y se logran formular definiciones de conceptos, incluyendo la elaboración de otras definiciones para conceptos ya definidos. Predomina el razonamiento lógico - abstracto; se realizan generalizaciones de contenido, es decir, sobre la base de las características o atributos relevantes de los objetos matemáticos, lo que permite formar los conceptos científicos.
Algunos autores como Freyer, Gahtala & Klausmeier (1972), citados por D`Amore (2001); y González (2005), hablan de la existencia de niveles en el dominio de conceptos en la escuela primaria. Otros como Ballester, et al. (2002); y Curbeira, et al. (2013), se refieren a la existencia de determinados niveles en el desarrollo de la capacidad para definir conceptos, pero lo cierto es que de lo que se trata es de niveles en el proceso de formación de conceptos, pues unas veces se habla de conceptos espontáneos o cotidianos, otras veces de conceptos empíricos y otras veces de conceptos científicos, que es el objetivo fundamental de la enseñanza de la Matemática en la escuela básica.
Es por la razón anterior que los autores de esta investigación, consideran más adecuado hablar de niveles en el proceso de formación de conceptos y son del criterio que para identificar esos niveles en el proceso de formación de conceptos es necesario considerar, en primer lugar, el Modelo de Van Hiele (1957), citado por Ricaldi (2014), que establecen determinados niveles en el desarrollo de la capacidad de razonamiento geométrico de los estudiantes y, por otro lado, el modelo de Pirie & Kieren (1991, 1992), citado por Mel (2003), que establecen determinados niveles en el desarrollo de la comprensión Matemática y que ejemplifican con la comprensión de conceptos.
Según el modelo de los Van Hiele, existen cinco niveles en el desarrollo de la capacidad de razonamiento geométrico de los estudiantes: nivel de reconocimiento o visual, nivel de análisis, nivel de clasificación, nivel de deducción, y el nivel de rigor, mientras en los tres primeros niveles se requiere de un soporte concreto, es decir, de objetos que sean representantes del concepto para desarrollar su actividad, en los dos últimos niveles, se puede prescindir de ese soporte visual y se opera con sistemas axiomáticos diferentes y se puede analizarlos y compararlos, se encuentra en el máximo nivel de rigor matemático.
El modelo de comprensión Matemática de Pirie & Kieren (1991, 1992), citados por Mel (2003), establece siete niveles o estratos en el desarrollo de la comprensión Matemática, estos niveles son: nivel del conocimiento primitivo, nivel de creación de imágenes, nivel de comprensión de la imagen, nivel de observación de la propiedad, nivel de formalización, nivel de observación, nivel de estructuración y, nivel de invención (inventizing).
Al hacer un análisis de estos dos modelos, sobre la base de sus similitudes y diferencias, se pueden determinar cincos niveles en el proceso de formación de conceptos matemáticos en la escuela, que son:
Nivel visual: los estudiantes forman conceptos de manera espontánea, sobre la base de la experiencia y de las actividades que desarrolla el estudiante en el contexto en que viven: la comunidad, la familia. En este nivel el estudiante utiliza los conceptos, se forma una imagen del mismo, pero no tiene conciencia de sus atributos irrelevantes ni irrelevantes. En este nivel el concepto se asocia a su imagen y a un nombre, que predomina en la solución de cualquier tarea en la que haga referencia al concepto.
En este nivel, propio de la educación preescolar, abarca aspectos del nivel I del modelo de los Van Hiele (1957), citado por Ricaldi y de los niveles o estratos I, II y III, del modelo de Pirie & Kieren (1991, 1992), citados por Meel.
Nivel de Distinción: Se reconocen los atributos del concepto; pero no diferencian los relevantes o irrelevantes. Se establecen relaciones entre los conceptos y sus atributos, y entre los conceptos; pero siempre tomando como referencia el concepto imagen. En este nivel se realizan descripciones, caracterizaciones y ejemplificaciones del concepto.
Este nivel contiene elementos del nivel II del modelo de los Van Hiele (1957), citado por Ricaldi (2014); y de los niveles IV y V del modelo de Pirie & Kieren (1991, 1992), citados por Mel (2003).
Nivel formal: en este nivel el estudiante logra determinar los atributos relevantes del concepto a partir de sus atributos comunes. Se define formalmente el concepto con ayuda de conceptos genéricos (concepto superior) y los atributos que lo diferencian del concepto genérico. Se comprende la estructura lógica de una definición Matemática.
Este nivel incluye elementos de los niveles III y IV del modelo de los Van Hiele (1957), citado por Ricaldi (2014); y del nivel VI del modelo de Pirie & Kieren (1991, 1992), citados por Mel (2003).
Nivel de Innovación: En este nivel tiene lugar la formación inventiva de conceptos, donde los conceptos científicos no se extraen de la experiencia, sino que se crean, se construyen para lograr la máxima organización de la información existente. En este nivel los conocimientos que ya se tienen se utilizan desde un nuevo punto de vista para elaborar nuevas definiciones, lo que se conoce como definición innovadora de conceptos o para crear nuevos conceptos como resultado de la unión de hechos y conceptos que se formaron durante la enseñanza y que aparentemente resultan dispersos e independientes, por ejemplo, el concepto de cuadrilátero.
Los estudiantes de la Educación Básica Secundaria, con la guía del profesor, pueden llegar a definir innovadoramente un concepto ya definido, mientras que en el nivel preuniversitario pueden crear nuevos conceptos, como, por ejemplo, el concepto poliedro, que unifica los conceptos cubo, ortoedro, prisma, pirámide.
En el nivel innovador la creatividad del estudiante alcanza su máximo nivel de expresión, pero ello requiere de la enseñanza de determinadas acciones, tanto desde el punto de vista lógico, como psicológico, tales como, pasar a otro nivel de organización, cambiar el principio de organización, cambiar el centro- poniendo como esenciales los rasgos que eran secundarios, entre ellas generalización, división o concretización, centración o descentración. Acciones que al decir de la Talízina (1989), no siempre se enseñan en la escuela.
A juicio de los autores de esta investigación, el nivel de innovación, se considera cono el máximo nivel de desarrollo de la capacidad para definir conceptos de los estudiantes, por lo que no concuerdan con Ballester (2002), cuando afirman que el último nivel es la elaboración de la definición, ni con Curbeira, et al. (2013), cuando plantean que el último nivel es el de generalización, debido a que ella está presente en todas las etapas y niveles del proceso de formación de conceptos.
En este último nivel que se propone, se manifiestan los dos niveles máximos del desarrollo de la capacidad de generalización de conceptos identificados por Harel & Tall (1991), citados por Mel (2003).
Es importante señalar algunas características importantes de los niveles:
2. La jerarquización y secuencialidad de los niveles (Jaime & Gutiérrez, 1990). Es evidente que los cuatro niveles planteados representan distintos grados de complejidad en el proceso de formación de conceptos por parte del estudiante. Además, cada nivel se apoya en el anterior. Por ejemplo, no es posible pasar al nivel identificado como distinción, sin recurrir al nivel I, es decir, al concepto imagen y los objetos mentales asociados a él.
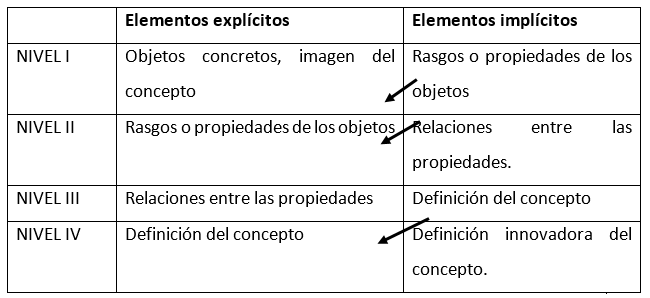
De esta manera, en el nivel I, hay determinados elementos explícitos, como son los objetos concretos, y determinados elementos implícitos como son, las partes y propiedades de los objetos, que se hacen explícitos en el nivel II y así ocurre en todos los niveles. La tabla 1, ilustra la estructura recursiva de los niveles:
Hay una estrecha relación entre las acciones y operaciones (psíquicas y prácticas) y los niveles. A cada nivel en el proceso de formación de conceptos le corresponden determinadas acciones psíquicas y prácticas, por ejemplo, en el nivel I, predominan acciones como la manipulación de objetos y figuras, la observación y la percepción, que son acciones necesarias para la formación del concepto imagen.
Pero no se debe olvidar, hay acciones que se realizan en todos los niveles, pero con diferentes grados de complejidad, por ejemplo, en todos los niveles se realizan clasificaciones (divisiones de conceptos), pero un grado de complejidad creciente, así en el nivel I, los conceptos se clasifican por su semejanza, en el nivel II, atendiendo a las propiedades, en el Nivel III, atendiendo a las propiedades comunes y en el nivel IV, atendiendo a las propiedades esenciales y relaciones lógicas entre los conceptos.
El paso de un nivel a otro se produce de forma gradual, progresiva. En el proceso de formación de conceptos las acciones psíquicas y prácticas que realizan los estudiantes, están estrechamente relacionadas con su nivel de preparación y desarrollo, fundamentalmente con el desarrollo del lenguaje y del pensamiento.
No se puede pretender que los estudiantes de la básica primaria definan formalmente un concepto, pues el pensamiento lógico - deductivo comienza desarrollarse en la básica secundaria, lo cual no quita que en este nivel educativo se pueda recurrir a los niveles I y II, en el trabajo en el nivel III.
De la misma manera en que se establecen relaciones entre los niveles, también se pueden establecer relacione entre las etapas y niveles del proceso de formación de conceptos. Estas relaciones se ilustran en la Figura 1.
Los autores consideran que tanto las etapas como los niveles determinados en el proceso de formación de conceptos deben considerarse en cualquier propuesta didáctica dirigida a la formación de conceptos en el proceso de enseñanza - aprendizaje de la Matemática en la Educación Básica Secundaria, donde debe prestarse especial atención, además, al rol de la actividad de los estudiantes en este proceso.
Es en el proceso de la actividad y sobre la base de esta, que se revelan las propiedades y nexos de los elementos de la realidad. A su vez el papel de los diversos tipos de actividad en la formación de los conceptos es diferente. Por ejemplo: la actividad objetal (manipulación y traslado) es necesaria para que las cosas y fenómenos demuestren sus propiedades; la perceptiva (percepción y observación), para que estas propiedades se reflejen en las percepciones y representaciones; la mental (análisis y síntesis) para comparar estas propiedades y destacar las que son comunes; la verbal (designar y nombrar) para fijar estas propiedades comunes haciendo abstracción de los objetos y generalizándolas como rasgos de las clases.
Vías, procedimientos y principios a tener en cuenta en la formación de conceptos matemáticos
Varios investigadores en el área de la Educación Matemática (Didáctica de la Matemática) han contribuido con estudios teóricos y prácticos a esclarecer las particularidades del proceso de formación de conceptos matemáticos, con el propósito de buscar las vías y los procedimientos más idóneos para formarlos, entre ellos se encuentran: Lovell (1969); Skatkin (1973); Skemp (1980), citados por González (2005). También, Charles (1980); Zilmer (1981) y Jungk (1989), citados por Ballester et al. (2002); y Turégano (2006).
Estudios realizados por Lovell (1969), citado por González (2005), con profesores de Matemática le permitieron reconocer que no hay consenso entre los docentes acerca de qué hacer para formar los conceptos matemáticos incluidos en el currículo, identificando dos tendencias.
Un primer grupo opinan que debe hacerse uso de materiales tomados de la experiencia cotidiana, en lugar de utilizar objetos y aparatos especiales. Los partidarios de este punto de vista afirman que, a través de un amplio conjunto de actividades y experiencias, el estudiante abstrae, asimila e intelectualiza el problema, se da cuenta del significado de sus propias acciones y, en consecuencia, no hay necesidad de una enseñanza directa.
Un segundo grupo opina que se deben utilizar procedimientos específicos y especialmente dirigidos y diseñados para completar las otras experiencias; en este caso el alumno manipula el material; contesta preguntas y hace selecciones que le permiten formular, conscientemente las relaciones y propiedades del material que maneja.
Los autores de esta investigación reconocen que ambas opiniones son válidas y que la segunda debe complementar la primera, pero no están de acuerdo con el hecho de que no es necesaria una enseñanza directa como lo plantea el primer grupo, de modo que ambas opiniones es necesario tenerla en cuenta en cualquier propuesta dirigida a la formación de conceptos matemáticos.
Por su parte, Skatkin (1973), citado por González (2005), explica el proceso de formación de un concepto del modo siguiente: cuando un objeto es percibido, no es aislado totalmente de la realidad que lo rodea, sino que es comparado y confrontado con los demás para, de ese modo, determinar semejanzas y diferencias entre ellos y poder agruparlos; al compararlo con los demás es posible notar qué es lo que cada objeto percibido tiene en común con otro objeto.
En el transcurso de esta actividad se hace abstracción de las propiedades circunstanciales y no sustanciales de los objetos y se forman los conceptos. Así que, para formar un concepto, el alumno debe observar objetos y fenómenos concretos, comparándolos entre sí para determinar semejanzas y diferencias entre ellos y distinguir lo sustancial de lo secundario.
Según Skemp (1980), citado por González (2005), un concepto requiere para su formación de un cierto número de experiencias que posean algo en común y capacidad, por parte de quien aprende, para aislar mentalmente y considerar por separado, la característica o características comunes que tengan dichas experiencias; es esta actividad abstractiva la que permite la formación del concepto. Éste, puede ser definido como generalización hecha a partir de datos relacionados que permitan responder o pensar en estímulos de un modo determinado.
Por su parte, Ballester, et al. (2002), describe la formación de conceptos como el proceso que va desde la creación del nivel de partida, la motivación, pasando por la identificación de las características comunes y no comunes, la determinación de las características esenciales, hasta llegar a la definición del concepto.
Una propuesta similar la realiza Turégano (2006), quien ofrece una explicación del proceso de formación de conceptos basada en la teoría de Vinner y sus colaboradores. Según esta autora, adquirir un concepto significa, adquirir un mecanismo de construcción e identificación mediante el cual será posible identificar y construir todos los ejemplos del concepto tal y como este está concebido por la comunidad matemática y prosigue señalando que en todo ejemplo del concepto se encuentran atributos relevantes y atributos irrelevantes.
En relación con las vías para la formación de conceptos, Ballester, et al. (2002), coincidiendo con González (2005), reconoce que se utilizan dos vías o estrategias que son la vía inductiva y la vía inductiva, aunque Ballester, et al., añaden otra vía, que es la vía constructiva.
Utilizando la vía inductiva se parte de ejemplos. El concepto se desarrolla partiendo de explicaciones y descripciones hasta llegar a la explicación o definición. Esta vía parte por lo tanto de lo particular (contenido) a lo general (extensión) y cuenta con los siguientes pasos: asegurar el nivel de partida; motivar y orientar hacia el objetivo; poner a disposición de los alumnos objetos de análisis (representantes o representaciones del concepto); analizar los objetos respecto a las características comunes y no comunes, establecer un sistema de características necesarias y suficientes (rasgos esenciales del concepto) y la definición o explicación del concepto.
Por su parte en la vía deductiva se parte de la definición del concepto y mediante el análisis de ejemplos se descubre el contenido. Esta vía conduce, por tanto, de lo general a lo particular. De ello resultan los siguientes pasos: asegurar el nivel de partida; motivar y orientar hacia el objetivo; presentar la definición y analizar cada una de las partes (definiendum - definiens); poner a disposición de los alumnos ejemplos y contraejemplos que deben ser examinados uno a uno según las características del concepto expresados en el definiens; analizar con los alumnos cual sería si se omitiese una característica; ordenamiento del concepto en el sistema de conocimiento.
La vía constructiva, considerada por Ballester, et al. (2002), como una modificación de la vía inductiva, se utiliza cuando no es posible poner a disposición de los estudiantes objetos que sean representantes del concepto que se desea formar ya que estos no son conocidos por ellos y se requiere entonces construir esos objetos. Utilizando esta vía se siguen los siguientes pasos: motivación y orientación hacia el objetivo, averiguar un principio para la construcción de estos objetos y construir los objetos.
Como se puede apreciar las tres vías son de gran utilidad para la formación de conceptos, pero lo que describen los autores es el proceder metodológico cuando se utilizan una u otra vía y lo importante es esclarece cuáles son las acciones y operaciones que deben ejecutar los estudiantes cuando forman (construyen) un concepto, aspecto este.
Al respecto, Talízina (1988), refiere que: “Basándonos en la comprensión de la psiquis como actividad, se llega a la conclusión de que cualquier imagen sea percepción, representación o concepto debe estar relacionada con un determinado sistema de acciones. De esta manera, la formación de los conceptos es un proceso de formación no solo de una imagen especial como cuadro del mundo, sino igualmente de un determinado sistema operacional que tienen su estructura interna”. (p.153)
Las acciones intervienen como medio de formación de los conceptos y como medio de su existencia: al margen de las acciones el concepto no puede ser asimilado ni aplicado posteriormente a la solución de problemas. Por ello, las particularidades de los conceptos formados no pueden ser comprendidas sin la orientación a la actividad cuyo producto representan (Talízina, 1988).
Los autores coinciden con la afirmación anterior, pues el proceso de formación de conceptos no incluye solo el concepto, la representación o la imagen, sino, también, las acciones y operaciones que permiten construirlo, identificarlo.
Con respecto a los principios, Dutton (1969), citado por González (2005), propuso una serie de principios generales que sirven para orientar el proceso de enseñanza-aprendizaje de los conceptos matemáticos. Según este autor para poder extender y generalizar la comprensión de un aspecto de la matemática se debe hacer énfasis en la comprensión de los conceptos involucrados en dicho aspecto y que, el lenguaje y los símbolos matemáticos se deben enseñar en forma gradual de tal modo que los estudiantes puedan comunicarse satisfactoriamente, tanto en forma verbal como escrita.
Para este autor, el docente, mediante una actitud estimuladora, debe incrementar el pensamiento y las experiencias matemáticas de los estudiantes de modo que éstos puedan alcanzar niveles más altos de abstracción matemática. Esta idea refuerza la necesidad de observar determinados niveles en el proceso de formación ce conceptos, de lo cual se habló anteriormente.
Las experiencias matemáticas, deben adecuarse al grado de madurez intelectual alcanzado por los estudiantes y se debe tener en cuenta que los conceptos matemáticos se derivan a partir de una significativa comprensión de las operaciones y/o manipulaciones ejecutadas sobre materiales concretos y no de los materiales mismos.
Por su parte, Skemp (1980), citado por González (2005), formuló dos principios para estructurar el proceso de aprendizaje y enseñanza de conceptos matemáticos, tomando como base la estructura de la Matemática, que son: (1) los conceptos matemáticos de un orden superior al de aquellos que poseen los estudiantes no pueden ser comunicados sólo mediante la definición verbal sino a través de una adecuada colección de ejemplos; (2) como en la Matemática esos ejemplos involucran otros conceptos, es preciso asegurarse que éstos ya han sido adquiridos por los estudiantes.
Dienes (1970), citado por González (2005), diseñó una serie de secuencias didácticas para la formación de conceptos por parte de los estudiantes, regidas por los siguientes principios:
Principio dinámico: Deben incluirse actividades prácticas o mentales que provean de la necesaria experiencia fundamental.
Principio de constructividad: Esencialmente implica la inducción desde lo particular a lo general (en contraste con el análisis que va de lo general a lo particular).
Principio de variabilidad matemática. Debe variarse la estructura matemática a partir de la cual el nuevo concepto o proceso se desarrolla para permitir que se distingan claramente todas las características matemáticas implicadas.
Principio de variabilidad perceptiva: Debe variarse suficientemente el marco de experiencia a partir del cual se desarrollan ideas y procesos al objeto de prevenir su fijación en un conjunto o conjuntos particulares de experiencias.
El principio de variabilidad perceptiva, afirma Dienes, es importante porque si no se ponen ejemplos concretos variados de un concepto puede suceder que los alumnos tomen como atributos relevantes del concepto aquellos que no lo son. Las variaciones matemáticas clarifican hasta qué punto se puede generalizar un concepto extendiéndolo a otros contextos.
Los autores de esta investigación reconocen el valor, desde el punto de vista didáctico de los principios identificados por Dutton, Dienes y Skemp, para la formación de conceptos matemáticos, pero a la vez considera que no son suficientes y que se requiere de un nuevo sistema de principios para sustentar una propuesta didáctica para la formación (construcción) de conceptos en la Educación Básica. Donde algunos de ellos pueden aparecer de manera implícita o explícita.
De modo que es necesario incluir otros principios que tengan en cuenta el rol de las representaciones mentales y la relación de estas con los conceptos, así como, el contexto, tanto cotidiano como matemático en la formación de conceptos, lo cual será objeto de estudio en otros trabajos.
Conclusiones
El proceso de formación (construcción) de los conceptos matemáticos en la escuela básica no transcurre de la misma forma en los diferentes niveles del sistema educativo, pues ello está en correspondencia con la edad y el nivel de desarrollo alcanzado por el alumno. Ello hace posible la identificación y determinación de diferentes etapas en este proceso.
Los conceptos matemáticos que se estudian en la escuela, se forman progresivamente y son ampliados y profundizados en cada nivel educativo en la medida que son encontradas nuevas instancias de él y son establecidas sus relaciones con otros conceptos del mismo sistema conceptual al cual pertenece, lo que permite identificar determinados niveles en el proceso de su formación.
Para estructurar, desde el punto de vista didáctico, el proceso de formación de conceptos matemáticos en la escuela, no basta con conocer las particularidades de este proceso, es decir, sus etapas y los niveles, sino que es necesario elaborar un sistema de principios que sirvan de base para una correcta concepción de este proceso.