Introducción
En la actualidad, la estadística se ha convertido en un área de conocimiento de gran reconocimiento y relevancia, debido a su vinculación con otras materias (sociales, científicas o humanísticas) (Engel, 2019). Debido a la abundancia de datos estadísticos en los medios de comunicación, se requiere un conocimiento estadístico mínimo en diferentes situaciones de la vida cotidiana para poder informarse sobre temas variados, y poder opinar críticamente sobre ellos. En este sentido, surge la idea de la cultura estadística, Gal (2002), que resalta el entender esta disciplina como parte de la herencia cultural que debe recibir todo ciudadano, y resulta de la unión de dos capacidades:
Gal (2002), plantea a) Interpretar y evaluar críticamente la información estadística, los argumentos apoyados en datos o los fenómenos estocásticos que las personas pueden encontrar en diversos contextos, y b) discutir o comunicar sus opiniones respecto a tales informaciones estadísticas cuando sea relevante.
En particular, uno de estos elementos son los gráficos estadísticos, usados ampliamente en medios de comunicación, Cavalcanti, et al. (2010), y fundamentales para el análisis estadístico de datos (Arteaga, et al., 2016). Dada su relevancia social, y de la estadística en general, este contenido se ha incorporado a la enseñanza desde los primeros cursos de formación obligatoria. Es así, como en Chile, las directrices curriculares establecidas por el Ministerio de Educación (2012), dentro del eje de matemáticas Datos y probabilidades, presentan la enseñanza de los siguientes gráficos estadísticos: pictograma (1º a 4º), gráfico de barras simples, con escala o barras dobles (2º a 6º), puntos (3º y 6º), línea (5º), tallo y hojas (5º y 6º), y sectores (6).
El diagrama de puntos, en el que centramos esta investigación, se trabaja en forma discontinua, en 3º y 6º curso, según se menciona en los objetivos de aprendizaje de las directrices curriculares (Chile. Ministerio de Educación, 2012):
Tercer curso: “representar datos usando diagramas de puntos”.
Sexto curso: “comparar distribuciones de dos grupos, provenientes de muestras aleatorias, usando diagramas de puntos y de tallo y hojas”.
Además, en un análisis previo de los libros de texto chilenos de Educación Primaria, se ha comprobado que se trabaja este tipo de gráfico especialmente en los cursos recientemente mencionados (Díaz-Levicoy, et al., 2016).
El presente trabajo se apoya, por un lado, en algunas teorías sobre la comprensión y niveles de lectura de los gráficos estadísticos y, por otro lado, en los antecedentes de nuestra investigación.
En primer lugar, en la búsqueda de comprender la forma de leer un gráfico estadístico, se han planteado diferentes taxonomías que describen la mayor o menor competencia para interpretar el contenido de un gráfico. En ellas, utilizaremos los niveles de lectura de (Curcio, 1989; Shaughnessy, et al., 1996; Friel, et al., 2001), donde la complejidad depende de los objetivos matemáticos y estadísticos que se demandan para dar respuesta a la tarea:
N1. Leer los datos. Cuando únicamente se requiere realizar una lectura literal del gráfico estadístico. Requiere la comprensión de aspectos aislados de la representación, por ejemplo, identificar la variable representada en el eje Y, o la frecuencia que corresponde a un valor dado en un diagrama de líneas.
N2. Leer dentro de los datos. Conlleva, además de la lectura literal del gráfico estadístico, realizar comparaciones entre los datos u obtener un valor mediante cálculos aritméticos sencillos con ellos. Por ejemplo, cuando se pide calcular la media aritmética de una distribución de datos representada en un gráfico estadístico.
N3. Leer más allá de los datos. Cuando se deben predecir datos que no están representados en el gráfico estadístico, es decir, es necesario realizar una interpolación o extrapolación con la información. Por ejemplo, predecir la cantidad de agua que caerá en una ciudad de acuerdo con las precipitaciones de los 10 últimos años.
Nivel 4. Leer detrás de los datos. Corresponde a la valoración crítica del gráfico, de la forma en que se ha construido o bien de las afirmaciones que se hacen respecto a su contenido (conclusiones). Por ejemplo, cuando se discute la veracidad o falsedad de una afirmación sobre lo representado en el gráfico estadístico.
En segundo lugar, nos apoyamos en las investigaciones sobre la lectura de gráficos estadísticos, que se han centrado en los gráficos estadísticos con mayor presencia en los medios de comunicación y libros de texto. Las más relacionadas con nuestro trabajo se resumen a continuación.
Curcio (1981), analiza la relación de diferentes variables sobre la comprensión de gráficos estadísticos (barras, líneas, sectores y pictogramas) por 204 estudiantes americanos de 4º, y 185 de 7º curso, con un cuestionario de opción múltiple, donde, para cada tipo de gráfico propone 6 preguntas. Los resultados muestran un efecto estadísticamente significativo de la edad y el conocimiento matemático previo (medido por la calificación media los cursos anteriores) sobre dicha comprensión.
Canché (2009), evalúa, con un cuestionario de opción múltiple, la comprensión de gráficos estadísticos (dos pictogramas, dos gráficos circulares, dos gráficos lineales, uno de barras) en una muestra de 206 estudiantes mexicanos de 6º de Educación Primaria. Los resultados muestran que el 69,1% de los estudiantes, responden correctamente a las actividades de N1 (leer los datos), el 50,6% las de N2 (leer dentro de los datos) y el 47,5% las de N3 (leer más allá de los datos). Por ejemplo, en el gráfico de líneas, el 41% logran el N1, 43% el N2, y 26,7% el N3.
Fernández, & Morais (2011) evalúan la lectura de gráficos por 108 estudiantes de 9º grado de Portugal mediante una actividad por representación (gráfico de barras, sectores y líneas). Los resultados muestran que el 68% de los estudiantes responden correctamente las actividades de N1, el 33% a las actividades de N3, y 24% a las de N2. Las actividades sobre el diagrama de barras, el 90% alcanzan un N1, y el 23% un N2; el 96% logran un N1, el 31% un N2, y el 23% un N3 en el gráfico circular; el 19% logra un N1, el 14% un N2, y el 43% un N3 en el gráfico de líneas.
Fernández, Santos, & Pereira (2017), describen los resultados de una secuencia de enseñanza centrada en el trabajo con tablas y gráficos estadísticos con 35 estudiantes de 5º curso de Educación Primaria en Brasil. Comparan los resultados de un pre-test y un post-test, donde la lectura literal de un pictograma avanza de 63,3% al 100% de respuestas correctas; la lectura literal de un gráfico de barras de 86,6% a un 100%; y, finalmente, la comparación de valores de un gráfico de barras pasa de 77,1% al 97,2%, y la diferencia de frecuencias de 40% a 82,8%.
García-García, et. al. (2019), analizan la comprensión de un diagrama de sectores y uno de barras dobles por 78 estudiantes de 1º de Educación Secundaria (11-12 años) en México, antes y después de una intervención de aula. Los resultados evidencian un avance en los niveles de comprensión luego de la instrucción, pues la mayoría se encontraba en el N2 en el pre-test y alcanzar niveles superiores en el post-test.
De acuerdo con las consideraciones anteriores, y dado que no hemos encontrado antecedentes sobre la lectura del gráfico de puntos, además de los escasos de estudios en el contexto chileno, nos planteamos el objetivo de evaluar la capacidad de leer un diagrama de puntos por estudiantes chilenos de 6º y 7º de Educación Primaria. De esta forma ampliamos los resultados obtenidos al trabajar con otros gráficos estadísticos (Batanero, et al., 2018; Díaz-Levicoy, et al., 2019a; Díaz-Levicoy, et al., 2019b).
Desarrollo
Este trabajo sigue una metodología de tipo cualitativa y de nivel descriptivo, basada en el análisis de contenido (Neuendorf, 2016) de las respuestas escritas entregadas de los estudiantes a la tarea planteada.
La muestra de estudiantes que han participado en esta investigación estuvo formada por 745 estudiantes de Educación Primaria en Chile, 380 de 6º curso (11-12 años) y 365 de 7º curso (12-13 años), pertenecientes a 13 centros educativos de siete ciudades diferentes. Estos estudiantes tenían una edad media de 12, 13 años, siendo el 50,9% mujeres y el 49,1% hombres en el momento de aplicar el instrumento. Para dicha aplicación, se tuvo que negociar el acceso a las aulas con los encargados de los centros (directores) y los profesores que estarían en las salas de clases. Uno de los autores asistió personalmente a la cumplimentación del cuestionario, para la cual se dispuso de tiempo suficiente dentro de la clase de matemáticas. Para facilitar el análisis y la presentación de ejemplos en el artículo, asignamos a cada estudiante un código (Ex), donde x corresponde a un número del 1 al 745 de acuerdo al orden en que se han analizado las respuestas.
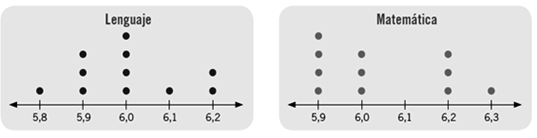
La tarea planteada se adaptó de un libro de texto de 6º curso de Educación Primaria (Fig 1) (Ávila, et al., 2013) y pretende evaluar la competencia de lectura crítica, en un gráfico de puntos, es decir, un nivel de lectura 4 (leer detrás de los datos) en la taxonomía de Curcio (1989); Shaughnessy, et al. (1996); Friel, et al., (2001).
Los siguientes diagramas corresponden a las calificaciones (entre 1,0 y 7,0) obtenidas por los niños de 6º curso en Lenguaje y Matemática.
María dice que las Matemáticas son más difíciles porque hay pocos niños con nota de 6 o más. ¿Estás de acuerdo? Explica por qué
En esta tarea se pide a los estudiantes en primer lugar indicar si están de acuerdo con la afirmación de María y se espera que digan que no están de acuerdo. A continuación, se les pide justificar la respuesta. Para ello los estudiantes han de leer la frecuencia con que cada valor de las puntuaciones aparece en cada uno de los dos gráficos, lo que requiere un nivel de lectura N1; a continuación, deben calcular la frecuencia que corresponde al valor 6 o mayor, que es 7 en los dos casos (Nivel de lectura N2). Al comparar con la afirmación de María, se ve que esta es falsa, pues, además, hay un niño con 5,8 en lengua y ninguno en matemáticas, donde hay un alumno más con 5,9 que en lengua. A continuación, analizamos los resultados.
En primer lugar, se consideran los resultados respecto a la veracidad o falsedad de la afirmación realizada por María, respecto a que la matemática es más difícil que el lenguaje, teniendo en cuenta la frecuencia de calificaciones iguales o superiores a 6,0 que muestran los diagramas de puntos. Se espera que los estudiantes muestren su desacuerdo con dicha información por las razones señaladas o bien porque la media es más alta en matemáticas.
En la Tabla 1 resumimos los porcentajes de estudiantes que muestran su acuerdo o desacuerdo con la afirmación realizada por María. En general, los estudiantes no están de acuerdo con esta afirmación (59,5%), es decir, según la información representada en los gráficos, la matemática no sería más difícil que el lenguaje. Los resultados por curso son similares, con una leve ventaja de los estudiantes de 6º (59,7%) sobre los de 7º (59,2%).
Tabla 1 - Porcentaje de estudiantes según valoración de la afirmación de María.
| Afirmación | 6º curso (n=380) | 7º curso (n=365) | Total (n=745) |
| Verdadero (Incorrecto) | 20,8 | 17,3 | 19,1 |
| Falso (Correcto) | 59,7 | 59,2 | 59,5 |
| No responde | 19,5 | 23,6 | 21,5 |
Le siguen los estudiantes que no indican si estaban o no de acuerdo con la afirmación realizada por María, que alcanzan un 21,5%; al comparar por curso, vemos que los de 7º son los que presentan mayor porcentaje de respuestas sin indicar si están o no de acuerdo con María (23,6%), frente a los de 6º (19,5%). Estos estudiantes no han sabido leer los datos o bien no saben cómo usarlos para responder. En tercer lugar (19,1%), están las respuestas de los estudiantes que mencionan estar de acuerdo con María, donde el 20,8% corresponde a los de 6º y el 17,3% a los de 7º curso. Estos estudiantes han realizado una lectura incorrecta de los gráficos pues llegan a una conclusión equivocada.
Seguidamente, se analizan los argumentos entregados por los estudiantes para justificar su respuesta, como una forma de aproximarnos al nivel de lectura que alcanza. Para dicho análisis utilizamos los niveles de lectura de Curcio (1989); Shaughnessy, et al. (1996); Friel, et al. (2001), según los siguientes criterios:
N0. No leer. Cuando el estudiante no responde a la tarea planteada o su lectura es incorrecta, es decir, no es ni capaz de realizar una lectura literal de la información. También se consideran en este nivel las respuestas basadas en apreciaciones personales sobre las matemáticas y su estudio (facilidad o dificultad), es decir, estudiantes que no tienen en cuenta los datos. Por ejemplo, la respuesta de E4, se basa en una percepción personal sobre el esfuerzo en el aprendizaje de las matemáticas; además, no es capaz de leer correctamente los datos representados (decimales).
Yo no estoy de acuerdo con María porque como niñas y niños sabemos y nos debemos esforzar para los estudios y hacer todo lo posible o todo el empeño para que les de 60, 61, 62, 63, etc. (E4).
N1. Leer los datos. Cuando el estudiante proporciona una respuesta basada en una lectura literal de alguno de los datos en los diagramas de punto, lo que implica leer bien algún elemento. Por ejemplo, E303 realiza una lectura de un elemento con frecuencia cero (lectura inversa):
Sí, porque nadie sacó un 6,1 (E303).
N2. Leer dentro de los datos. Cuando el estudiante, además de realizar una lectura literal de algún dato o información, realiza cálculos aritméticos sencillos o comparaciones con ellos. Pero, sus conclusiones no consideran todos los datos de las distribuciones o sus argumentos son imprecisos. Por ejemplo, E692 solo compara la cantidad de estudiantes con puntuación superior a seis en ambos diagramas y olvida el valor 5,8.
No, no estoy de acuerdo con María porque hay más alumnos con 6 (6,0, 6,2, 6,3) que con 5,9 (E692).
N3. Leer más allá de los datos. Cuando el estudiante realiza predicciones o inferencias sobre valores que no están representados en los diagramas. En esta tarea, no se aplica este nivel.
N4. Leer detrás de los datos. Cuando el estudiante realiza una valoración crítica de diferentes aspectos relacionadas con los diagramas de puntos: de la información mostrada, de la forma de organizarla o de las conclusiones obtenidas. En este caso, además de leer los datos y realizar comparaciones o cálculos, se debe indicar si comparte (o no) lo que dice María, y argumentar su opinión usando todos los datos mostrados en los diagramas. También, se aceptan aquellos argumentos que presenten leves imprecisiones. Por ejemplo, E42, además de identificar las calificaciones máxima y mínima de matemáticas y lenguaje, hace una comparación de la frecuencia de puntuaciones iguales o superior a 6.
No estoy de acuerdo ya que la misma cantidad de notas 6,0 y sobre 6: aparte la peor nota de matemáticas es 5,9 mientras que en lenguaje la peor es 5,8; también matemática tiene más notas sobre 6 que lenguaje y por otra parte la mejor nota es 6,3 y la de lenguaje es un 6,2 (E42).
La distribución porcentual de los niveles de lectura alcanzada por las respuestas de los estudiantes se muestra en la Tabla 2, de la cual vemos que el nivel de lectura más frecuente es N0 (no leer) (47,1%), es decir, las respuestas en blanco o que no son capaces de leer ni literalmente la información o bien que no han utilizado los datos, sino sus creencias personales para dar la respuesta.
Le sigue, con una pequeña diferencia, en segundo lugar, el N2 (leer dentro de los datos) (46,7%), donde los estudiantes comparan o aplican procesos matemáticos sencillos con los datos representados en el gráfico, pero o bien no llegan a justificar correctamente la respuesta o no tienen en cuenta todos los datos de la distribución. Son escasas las respuestas de los estudiantes que alcanzan el N4 (leer detrás de los datos) (1,2%), máximo exigido, y el N1 (leer los datos) (5%). Al comparar los resultados por curso, vemos que los de 7º obtienen peores resultados que los de 6º, porque casi la mitad de sus respuestas son categorizadas como de N0 (no leer) (49,3%). Respecto del N4, los resultados son mínimos en ambos cursos (1,1% en 6º y 1,4% en 7º).
Tabla 2 - Porcentaje de estudiantes según nivel de lectura alcanzado en la tarea.
| Nivel de lectura | 6º curso (n=380) | 7º curso (n=365) | Total (n=745) |
|---|---|---|---|
| 0 | 45 | 49,3 | 47,1 |
| 1 | 6,6 | 3,3 | 5 |
| 2 | 47,4 | 46 | 46,7 |
| 4 | 1,1 | 1,4 | 1,2 |
Finalmente, en tercer lugar, realizamos una valoración global del conocimiento mostrado por el estudiante en la actividad, dando a cada uno una puntuación, de acuerdo con los siguientes criterios (Fig 2):
Hasta 2 puntos (0: no selecciona; 1: incorrecto; y 2: correcto), al indicar que están o no de acuerdo con la afirmación realizada por María.
Hasta 4 puntos por el nivel de lectura (de 0 a 4 puntos, sin considerar el 3 que no se pide en la actividad) que alcanza la justificación realizada por el estudiante para avalar su postura.
De acuerdo con este criterio, un estudiante puede obtener una puntuación máxima de 6. Con dicha información se han construido los gráficos de la Figura 2, donde el diagrama de barras adosadas nos permite observar que la puntuación de mayor frecuencia es 4 puntos, sobre la mediana teórica (que serían 3 puntos), seguido de los 0 y 2 puntos. Además, de la comparación de los diagramas de cajas vemos que la mediana es igual en ambos cursos (2 puntos), bajo el valor teórico, y que los cuartiles uno y tres coinciden (1 y 4, respectivamente).
Respecto al nivel de lectura, observamos que un 52,1% de las respuestas de los estudiantes de encuadran en un N0 y N1 de lectura, mientras que tan solo un 1,2% está en el nivel más alto exigido (N4). Si comparamos los resultados por cursos, estos suelen ser similares.
Al comparar estos resultados con los trabajos descritos en los antecedentes, pese a abordar gráficos diferentes, vemos que estos resultados son deficientes. En particular el 50,6% de los niños de 6º curso de la investigación de Canché (2008), alcanzan el nivel N2 y el 77,1% de niños de 5º en el pretest de la investigación de Fernandes, et al. (2017), en Brasil, así como la mayoría de estudiantes de 1º de Educación Secundaria (equivalente a 7º en nuestro estudio) en el trabajo de García-García, et al. (2019).
En Díaz-Levicoy, et al. (2019a), fue también muy baja la proporción de niños que alcanza la lectura crítica de datos (N4), aunque algo mayor (6,6% en el pictograma, 11,6% en el gráfico de líneas, 7,9% en el gráfico de sectores en 6º curso, y algo mayor en todos los gráficos en 7º curso: 6,3% en el pictograma, 15,9% en el gráfico de líneas, 11,2% en el gráfico de sectores) y muy numerosos los que quedan en N0, especialmente en el gráfico de sectores y líneas (29,2% en 6º y 31,8% en 7º en el gráfico de líneas; 17,6% en 6º y 21,4% en 7º en el gráfico de sectores).
Conclusiones
Los resultados de nuestro trabajo evidencian las dificultades que tienen los estudiantes chilenos de 6º y 7º de Educación Primaria para realizar la valoración crítica de una afirmación basada en la información presente en un diagrama de puntos. Esto se refleja en que en torno a un 40% de los estudiantes no responden a la actividad o valoran incorrectamente la veracidad de la afirmación.
No obstante, en todas estas investigaciones se han utilizado gráficos de barras o líneas, por lo que la lectura del gráfico de puntos, no investigada hasta el momento puede ser de mayor dificultad para los estudiantes, lo que haría cuestionable el hecho de que en el currículo chileno aparezcan ya desde el 3º curso. Por otro lado, en nuestro trabajo se ha planteado una pregunta de nivel N4, de lectura crítica, mientras que este tipo de pregunta no se plantea en los trabajos citados.
Estos resultados nos invitan a reflexionar sobre la pertenencia de la enseñanza de los diagramas de puntos en 3º y 6º de Educación Primaria, ya que puede existir un efecto olvido al no trabajarse en los cursos intermedios. Además, se trata de un gráfico presente en los libros de texto para los niveles en que las directrices curriculares explicitan su enseñanza.
La lectura crítica de datos a N4, donde los estudiantes han de usar el gráfico para obtener alguna conclusión o discutir una afirmación es una tarea difícil para estos niños. Sin embargo, el objetivo de la educación estadística no debe ser sólo que los estudiantes lean los gráficos, sino que los puedan utilizar para obtener conclusiones o tomar decisiones. En este sentido sugerimos la necesidad de reforzar este tipo de actividad en el aula y completar la investigación relacionada con la competencia de los niños para la lectura crítica de gráficos.