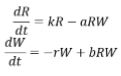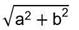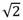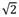Introducción
La educación es un fenómeno social, resultado del desarrollo histórico alcanzado, ejerciendo una influencia decisiva en la formación del hombre preparándolo para el disfrute y plenitud de todo aquello que se derive de ella, acorde en la sociedad en que vive. Ha de lograr el difícil equilibrio de ofrecer una respuesta educativa y comprensiva, proporcionando una cultura común a todos los individuos de la sociedad. Es por ello que se debe proporcionar a cada uno lo que necesita para potenciar al máximo sus posibilidades y su identidad. Luego, se hace necesario preparar a los estudiantes en la concepción científica del mundo, es decir, desarrollar en toda la plenitud humana las capacidades intelectuales, físicas y espirituales.
Al decir de (Monzón, 2016), en este sentido la Matemática desempeña un papel importante, su influencia se hace sentir no solo en las ciencias sino también en la enseñanza, la cual tiene entre sus objetivos centrales el ofrecer a todo ciudadano una preparación matemática sólida.
En el contexto de la enseñanza de la Matemática uno de los aspectos que atrae más la atención es la resolución de problemas como tareas docentes, esto constituye uno de los objetivos rectores en todas las enseñanzas. Con el trabajo con dichas tareas se debe lograr no solo la consolidación de los conocimientos matemáticos sino también la formación de la personalidad del alumno, es decir el desarrollo de su concepción científica del mundo y de la posición activa y crítica con respecto a los fenómenos, hechos naturales y sociales. Para esto es necesario seleccionar adecuadamente los ejercicios a través de los cuales es posible actuar sobre determinada esfera de la personalidad del alumno y explotar al máximo su contenido a partir del desarrollo de la función educativa. Una de estas atenciones es la Educación Ambiental desde la Matemática Superior en la Universidad.
La labor coherente de la escuela con las demás fuerzas educativas es condición indispensable para el desarrollo de una educación ambiental como alternativa de solución a los problemas ambientales, en función de instruir y educar a los estudiantes hacia el uso racional de los recursos naturales y socioeconómicos del medio ambiente.
De este encargo no están exentas las universidades, todo lo contrario, en ellas se deben planificar acciones para ofrecer tratamiento a la problemática ambiental desde la formación inicial de los futuros profesionales.
En la Estrategia Nacional de Educación Ambiental de Cuba (Cuba. Ministerio de Ciencia, Tecnología y Medio Ambiente, 1997), se plantea que se debe “introducir la dimensión ambiental con un carácter interdisciplinario, en los modelos del profesional, planes de estudio en sus componentes académico, laboral e investigativo, así como en los planes de ciencia y técnica del Sistema Nacional de Educación Superior”. (p.10)
Como se aprecia, la educación ambiental es una necesidad para enfrentar los problemas actuales del medio ambiente y para lograrlo es preciso contar con profesores preparados para su tratamiento. Es por ello que en la formación inicial del profesional de la universidad se debe prestar atención a su preparación respecto a la educación ambiental y no esperar a que esté graduado para ejecutar acciones en esa dirección.
Desarrollo
Dadas las estrechas relaciones entre educación científica y educación ambiental, Sauvé (2010), reconoce, no solo, que ambas pueden entrecruzarse de diversas maneras complementarias, sino también, la necesidad de su integración.
Sobre la base de estas relaciones algunos investigadores como Negev, et al. (2008), citados por Navarro (2017), hablan alfabetización científica ambiental. En este sentido establecen la existencia de tres categorías o componentes dentro del concepto de alfabetización científica ambiental: (a) conocimientos, que com prende temas de interés mundial y nacional y los principios ecológicos generales; (b) actitudes, que se refiere a la voluntad de actuar, el sentido de la responsabilidad, la sensibilidad sobre el medio ambiente y el aprecio por la naturaleza, y (c) comportamientos, que incluye patrones de consumo, conservación, activismo ambiental y contacto con la naturaleza.
Si se tiene en cuenta que el enfoque integral para la labor educativa en las universidades cubanas, tiene como principal objetivo transformar la personalidad del estudiantes, para alcanzar con ello niveles cualitativamente superiores en su desempeño profesional integral y que ello implica dotarlos de una sólida formación científica, sin la cual no puede haber, desempeño profesional integral (Horruitiner, 2006), así como la relación entre educación científica y educación ambiental, entonces se puede entender la tarea que le corresponde a las universidades en función de concretar acciones en el orden académico, laboral e investigativo formar un profesional a la altura de estos tiempo con una adecuada formación científico - ambientalista.
Para ello es necesario tener en cuenta, en primer lugar, la Agenda 2030 y los Objetivos de Desarrollo Sostenible (Bárcena, et al., 2018), de los cuales se seleccionan aquellos relacionados con este trabajo, como por ejemplo: “Adoptar medidas urgentes y significativas para reducir la degradación de los hábitats naturales, detener la pérdida de biodiversidad y, de aquí a 2020, proteger las especies amenazadas y evitar su extinción; 15.7 Adoptar medidas urgentes para poner fin a la caza furtiva y el tráfico de especies protegidas de flora y fauna y abordar tanto la demanda como la oferta de productos ilegales de flora y fauna silvestres; 15.c Aumentar el apoyo mundial a la lucha contra la caza furtiva y el tráfico de especies protegidas, incluso aumentando la capacidad de las comunidades locales para perseguir oportunidades de subsistencia sostenibles”
Todo lo anterior debe ser considerado a la hora de elaborar las situaciones docentes a proponer a los estudiantes en el desarrollo de la docencia, en correspondencia con el contenido de cada objetivo y su propósito a lograr.
Otro elemento a considerar para lograr el vínculo entre la Matemática Superior y la Educación Ambiental es lo relativo a la interdisciplinariedad. Para ello se asumió la definición de interdisciplinariedad expresada por Horruitiner (2008), en la que aborda esta como un proceso, una forma de pensar y proceder, que permite, al hombre conocer la realidad objetiva, poder resolver cualquiera de los complejos problemas que esta plantea.
Otro de los aspectos tratados gira alrededor de las condiciones para hacer posible la interdisciplinariedad, asumidos también del mismo autor, el cual plantea, que estas condiciones se basan en la competencia que debe poseer cada docente y el interés y motivación por llevar a cabo la interdisciplinariedad, el eficiente trabajo metodológico que debe desarrollar la institución, donde desempeñan un papel predominante los órganos de dirección y técnicos, a los cuales les corresponde la dirección del trabajo metodológico bajo la influencia de los factores comunitarios, aunado a la preparación metodológica que le corresponde atender a las universidades tanto en los estudios de pregrado como en los de postgrado con el objetivo de desarrollar en los profesores el enfoque interdisciplinar como una filosofía de trabajo.
Sobre las ventajas que ofrece el desarrollo de la interdisciplinariedad, que también son asumidos por este autor, se analizó la importancia de este proceso ya que elimina las fronteras entre las disciplinas, posibilita el aumento de la motivación en los estudiantes, así como una interrelación entre los conceptos que se desarrollan, y las definiciones con que opera el estudiante, permitiendo, además la sistematización de las habilidades y educando un pensamiento lógico, reflexivo e integrador a la vez que despierta el interés de los docentes y propicia entre ellos mejores relaciones de trabajo.
En los problemas del medio ambiente la humanidad tiene que trabajar sostenidamente por resolver los diversos problemas de carácter global, de cuya solución depende la existencia de la especie humana; y así la necesidad de la Educación Ambiental que se entiende como “un proceso continuo y permanente, que constituye una dimensión de la educación integral de todos los ciudadanos, orientada a la adquisición de conocimientos, desarrollo de hábitos, habilidades, capacidades y actitudes y en la formación de valores, que armonicen las relaciones entre los seres humanos y de ellos con el resto de la sociedad y la naturaleza, para propiciar la orientación de los procesos económicos, sociales y culturales hacia el desarrollo sostenible". (Valdés, 2007)
“Las Estrategias Curriculares aseguran el logro de objetivos que, por su alcance, rebasan las posibilidades de una disciplina, y por tanto, deben ser asumidos por todas o por una parte de éstas. Se concretan en cada uno de los años de la carrera, como parte de sus objetivos”. (Horruitiner, 2008)
La Estrategia de Educación Ambiental se propone como objetivos:
Fortalecer la incorporación de la educación ambiental para el desarrollo sostenible (EApDS), integrando la educación para la salud, energética y para el ahorro, en el proceso de formación inicial de los profesionales.
Educar a los profesionales en formación para la disminución del impacto de los desastres sobre el medio ambiente.
Fortalecer la EApDS, atendiendo los diferentes componentes del proceso de formación, de manera coherente, sistemática e integrada, incorporando a las organizaciones estudiantiles de la universidad.
Promover la participación de los medios masivos de comunicación en el desarrollo de la educación ambiental de los profesionales en formación.
Orientar, asesorar y controlar la actividad científica estudiantil en relación con la educación ambiental.
Evaluar sistemáticamente los niveles de participación de los estudiantes en formación en la EApDS, sobre la base de indicadores definidos.
Dentro de sus Lineamientos Teóricos se encuentran los Conceptos Básicos, los cuales se mencionan a continuación: medio ambiente, desarrollo sostenible, problema ambiental, educación ambiental, educación ambiental para el desarrollo sostenible (EApDS), desempeño profesional ambiental (DPPA) y formación ambiental inicial de los profesionales.
En el cuerpo de Estrategia Nacional de Educación Ambiental (2010-2015), Ministerio de Ciencia, Tecnología y Medio Ambiente (2010), se encuentran detallados como Temas Priorizados los siguientes: cambio climático, peligro, vulnerabilidad y riesgo, uso sostenible de Recursos Hídricos, conservación y uso sostenible de la diversidad biológica, manejo sostenible de tierra, lucha contra la contaminación del medio ambiente, manejo seguro de los productos químicos y desechos peligrosos, consumo y producción sostenible, manejo de la zona costera, derecho ambiental y participación ciudadana, protección del patrimonio natural y cultural.
Dentro de los Lineamientos Metodológicos se pueden nombrar las Exigencias Pedagógicas:
La unidad del medio ambiente natural y el social.
La unidad de lo afectivo, lo cognitivo y lo actitudinal.
El desarrollo y transformación de actitudes.
La unidad entre lo local, nacional, regional y global.
El mejoramiento de la calidad de vida.
La unidad entre el medio ambiente y el desarrollo.
En los contenidos se tiene en cuenta las siguientes ideas rectoras: a) los seres humanos como parte integrante del medio ambiente, se desarrollan en interrelación constante con la naturaleza, b) el mejoramiento de la calidad de vida de los seres humanos, constituyen las vías fundamentales que aseguran la supervivencia de las presentes y futuras generaciones, c) los seres humanos aseguran el mantenimiento de las condiciones del planeta con una actitud responsable en el medio ambiente.
En los objetivos por años del Modelo del Profesional se declara en común para el primer año de las carreras universitarias: describir las relaciones del hombre como ser biopsicosocial, en la problemática ambiental contemporánea a diferentes escalas, de manera que puedan estimular modos de pensar, sentir y actuar responsables con el medio ambiente en sus educandos.
Es por eso que los docentes universitarios deben tener en cuenta este propósito para la elaboración, diseño e implementación de las tareas docentes encaminadas a este fin.
Sobre las formas para lograr la Educación Ambiental desde las asignaturas del currículo, se requiere además del diseño y aplicación de las tareas docentes como complemento y base en la que se ha de buscar la vinculación de los conocimientos, y ello constituye un reto y a la vez una de las direcciones principales del trabajo metodológico en las asignaturas.
Varios autores han admitido que la tarea docente es la célula del proceso enseñanza-aprendizaje (Lompscher, et al., 1987). Para estos autores la tarea docente comienza a desarrollarse con el planteamiento del problema y es considerada como la célula, núcleo genético de los trabajos independientes, de modo que a su formulación hay que prestarle gran atención. Con la tarea orientada por el docente, cada estudiante ha de reflejar sus necesidades, motivaciones e intereses lo que permite evidenciar un conocimiento asimilado, una habilidad desarrollada, valores en formación. Se hace más individualizado y personificado el proceso de enseñanza-aprendizaje.
Por consiguiente, se puede expresar que la tarea docente tiene como fin desarrollar habilidades, concebidas estas, como un proceso dinámico e integrado de conocimientos, habilidades, actitudes y valores, que pueden ser inducidos y desarrollados durante el proceso docente, debiendo evaluarse su grado de apropiación.
“La tarea docente es la tarea que incluye los contenidos de las diferentes disciplinas y una vez que sean asimilados dialécticamente en su estructura cognitiva, posibilita que el estudiante pueda aplicarlos en su actividad práctica”. (Daudinot & Robert, 2014)
Son exigencias del diseño y aplicación de la tarea docente con fines formativos, las siguientes:
Incluir contenidos de varias asignaturas o disciplinas.
Potenciar la formación de destrezas, habilidades.
Los contenidos deben tener vínculos con los problemas profesionales.
El estudiante debe percibir su utilidad (para qué se realizará, con qué fin, qué aporta).
Debe contener las orientaciones precisas para resolverlas y tiempo de desarrollo.
Debe tener variantes para ampliar la participación individual y en equipo de los estudiantes.
En la enseñanza de la Matemática se utilizan las llamadas tareas matemáticas como un caso particular de tareas docentes, es decir, los ejercicios, problemas o actividades de contenido matemático que se realizan en la clase (Cázares, et al., 2020). Corresponde a los profesores crea las condiciones propicias en el proceso de enseñanza - aprendizaje de la Matemática para desarrollar en los estudiantes su independencia y creatividad, de modo que reflexionen y regulen sus acciones al solucionar dichas tareas, lo que contribuye a su vez a la formación de cualidades para la solución de problemas de su profesión.
Para ello, es pertinente la planificación, organización, dirección y control del trabajo, con una buena orientación y estructurada en etapas y fases de desarrollo de las diferentes tareas a ejecutar en la solución del problema, para alcanzar los objetivos y formar las habilidades.
Los autores de este trabajo definen las siguientes acciones: 1) Lo primero que se debe lograr es el diagnóstico ambiental y de las necesidades para el desempeño profesional ambiental de los estudiantes, como punto de partida; 2) La comprensión, por parte de los docentes y de los directivos de cada facultad, en particular, de la necesidad de incorporar la EApDS al proceso de enseñanza aprendizaje de las matemáticas en la universidad; 3) La preparación de los docentes y de los directivos de cada facultad, para la incorporación de la EApDS a este proceso, desde el sistema de trabajo metodológico, en cada nivel; y 4) La motivación de los estudiantes en formación y de los dirigentes de las organizaciones estudiantiles, para incorporar la EApDS a su quehacer diario.
Para el diseño de las tareas docentes debe considerarse que: la motivación puede aumentar si las situaciones de aprendizaje se derivan de la observación de los diferentes aspectos o temáticas que pueden ilustrarse mediante la proyección de videos, u otros recursos que devengan en medios atractivos para los alumnos; los partidarios de este punto de vista creen que el conocimiento medioambiental de los diferentes fenómenos que se presentan despertaría el interés y el cambio de actitudes de los alumnos por los contenidos matemáticos objeto de enseñanza.
Para diseñar tareas docentes con el propósito de utilizar la Educación Ambiental en la enseñanza de Matemática, se debe tener en cuenta, no solo el contenido, sino también, la concepción psicopedagógica en la que se sustenta el proceso de enseñanza - aprendizaje, en el caso particular de la universidad cubana, este proceso se fundamenta en el enfoque desarrollador.
De acuerdo a lo analizado en este trabajo, los autores consideran necesario destacar un grupo de aspectos que es necesario tener en cuenta en el diseño de las tareas. Estos aspectos son:
Los objetivos generales de la carrera, los objetivos del año específico y los objetivos de cada una de las disciplinas.
Las invariantes de cada una de las disciplinas incluyendo la Estrategia de Educación Ambiental.
El enfoque sistémico de las tareas como caso particular de las tareas docentes.
La secuencialidad de las tareas. Este aspecto se refiere al orden en que se irán presentando las tareas. Aquí debe tenerse presente su grado de complejidad y de dificultad.
La cantidad o volumen de tareas que se orientarán considerando la salida de la Estrategia de Educación Ambiental.
El momento en que se orientarán. En este aspecto debe considerarse la lógica del desarrollo de los contenidos, por lo que es necesario determinar los contenidos asimilados por el alumno hasta el momento en que estas se van a orientar, de manera que puedan hacer uso de ellos en su solución.
Indicadores a tener en cuenta para la evaluación de las tareas.
Muchos son los medios de enseñanza con que hoy un profesor dispone en las universidades cubanas, desde la tradicional pizarra, los libros, la prensa, láminas, fotos, esquemas, gráficas, tablas, dibujos, pinturas, maquetas, mapas, esferas, muestras de objetos naturales, computadoras, dispositivos móviles, videos, televisión, la radio, grabaciones, etc. Todos son oportunos y necesarios siempre que el pedagogo los emplee certeramente, oportunamente y logre en sus alumnos un aprendizaje significativo y desarrollador.
Ninguno de los aspectos del epígrafe anterior se puede obviar en el momento de concebir las tareas docentes que se les plantearán a los alumnos. Es importante que en cada una de las tareas se tenga en cuenta por los profesores los objetivos de la Estrategia del 2030, los objetivos del documento de la Estrategia Nacional de Educación Ambiental y el de cada problema que se trabajará, así como resaltar los aspectos educativos de lo que corresponde a la parte medioambiental, tanto por parte de los estudiantes como de los docentes y explotar al máximo las potencialidades que brinda la tarea en cuestión.
Tributar a que los estudiantes manifiesten sus ideas abiertas acerca del tema que se aborda en la tarea docente sin ser interrumpido por ningún compañero, siempre rectificando su vocabulario técnico y científico, y teniendo en cuenta las deficiencias detectadas en el diagnóstico fino para contribuir de esta forma a la erradicación de sus posibles errores y su superación.
Muchos problemas de crecimiento poblacional pueden ser modelados aplicando herramientas matemáticas. Los problemas de crecimiento poblacional conllevan a ecuaciones que son conocidas como ecuaciones de Lotka-Volterra o Sistema Depredador-Presa, otros problemas pueden ser del tipo recursivo. Estas ecuaciones tienen la forma:
k,r,a,b son constantes positivas que representan las interacciones entre los depredadores y las presas y t es el tiempo. El término aRW determina la velocidad con que disminuye la presa y bRW es la velocidad con que aumenta los depredadores. Vamos a llamar a R por la cantidad de presas en una zona y a W como la cantidad de depredadores en dicha zona (Stewart, 2008).
Referente a la solución de ecuaciones recursivas hay que rescatar una serie de aspectos que se estudiaron en el trabajo de ecuaciones diferenciales y esos son:
Soluciones generales de una ecuación diferencial.
Trabajo de ecuaciones diferenciales con valores iniciales
Una ecuación recurrente tiene la forma cnan+cn-1an-1+…+cn-kan-k=f(n); k∈Z+ y cada ci≠0 (constante) n≥k. La relación se define como homogénea si f(n)=0 en caso contrario se define como no homogénea; se define lineal si no hay términos elevados al cuadrado o no hay productos de aj. Cuando se resuelve una recurrencia pueden presentarse tres casos en dependencia de las soluciones obtenidas; puede que no se repitan, que se repitan o que sean resultados complejos; algo que no se considerará como un caso especial es el cambio de variable que se utiliza para resolver ecuaciones recurrentes un poco más complejas llevando la misma a una forma sencilla, sin embargo, será abordado para tener una idea de cómo usarlo. Los autores proponen al lector revisar el método de resolución de relaciones recurrentes no homogéneas en los libros Discrete and Combinatorial Mathematics And Applied Introduction de Ralph Grimaldi, 2004. Los métodos para la resolución de ecuaciones recursivas son equivalentes a los métodos utilizados para resolver ecuaciones diferenciales, la mayoría de los métodos que se abordaran aquí se derivan del trabajo con coeficientes indeterminados en una ecuación diferencial. Las soluciones ya sea por una ecuación recurrente o diferencial coincidirán si el problema está bien modelado.
Caso 1: an= 2an−1 + 3an−2 con a0= 1, a1= 2 (Lipschutz, 2007).
La solución general se obtiene al encontrar su polinomio característico P(x) y sus raíces r1 y r2. Para llegar al polinomio característico se puede hacer la sustitución an=crn, eso nos llevaría a:
crn=2crn-1+3crn-2
crn-2crn-1-crn-2=0 /:cr n-2
r2-2r-3=0
P(x)=r2-2r-3=(r-3) (r+1); raíces r1=3, r2=-1
an= c13n + c2(−1)n
En este punto hay que señalar que la ecuación anterior es una solución general así que para distintos valores de c1 y c2 se obtienen infinitas soluciones. Para hallar las soluciones específicas se realiza
Para n=0 y a0= 1, se obtiene: c130+ c2(−1)0= 1 o c1+c2=1
Para n=1 y a1= 2, se obtiene: c131+ c2(−1)1= 2 o 3c1-c2=2
Tras resolver el sistema se obtiene los valores de
c1=3/4 y c2=1/4
Por tanto, la solución única de la relación de recurrencia dada con las condiciones iniciales dadas a0= 1, a1= 2 es:
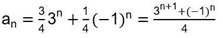
Caso 2: an= 6an−1− 9an−2
P(x)=r2-6r+9=(r-3)2 an= c13n+ c2n3n
La solución única se obtiene al encontrar c1 y c2 mediante las condiciones iniciales:
Para n= 1 y a1= 3, se obtiene: c131+c2(1)(3)1= 3 o 3c1+3c2=3
Para n= 2 y a2= 27, se obtiene: c132+c2(2)(3)2= 27 o 9c1−18c2= 27
Al resolver el sistema de ecuaciones con dos incógnitas c1 y c2 se obtiene:
c1=−1 y c2= 2
Por tanto, la única solución de la relación de recurrencia con las condiciones iniciales dadas es:
an=−3n+ 2n3n= 3n (2n− 1)
De forma más general, si r es una raíz del polinomio característico y tiene multiplicidad m entonces la solución general tendrá la forma: an=c1rn+c2nrn+c3n2rn+…+cm-1nm-1rn=0
Caso 3: an= 2(an-1- an-2). (Grimaldi, 2004)
El polinomio característico de la ecuación recurrente es r2-2r + 2 = 0 las soluciones a este polinomio son r1,2=1±i.
La solución general será: an=c1(1+i)n+c2(1-i)n
Para no dejar la expresión anterior expresada en términos de números complejos, se procede a aplicar el procedimiento para llevar de un número complejo a una expresión que ofrezca números reales. Haciendo referencia a los números complejos y utilizando el teorema de DeMoivre, se puede obtener:
tan Φ=b/a (cos Φ +isenΦ)n=(cosnΦ +isennΦ)
Entonces, aplicando lo anterior se tiene:
an= c1 (
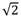 (cos (π/4) +isen (π/4)))n+ c2(
(cos (π/4) +isen (π/4)))n+ c2(
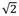 (cos (π/4) -isen (π/4))n
(cos (π/4) -isen (π/4))n
= c1 ((
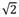 )n(cos (nπ/4) +isen (nπ/4)))+ c2((
)n(cos (nπ/4) +isen (nπ/4)))+ c2((
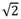 )n(cos (nπ/4) -isen (nπ/4)))
)n(cos (nπ/4) -isen (nπ/4)))
Una vez llegado hasta aquí se procede como en los casos anteriores en caso de estar la ecuación sujeta a condiciones iniciales.
Método Cambio de variable: T(n)=4T(n/2)+n para n>1
Aquí se reemplaza n por 2k (esto es k = lg n) para obtener T(2k) = 4T(2k-1)+2k.
Esta puede ser escrita tk = 4tk-1+2k, si tk=T(2k)=T(n). Conocemos ahora como resolver esta nueva recurrencia, la ecuación característica es (x-4)(x-2) = 0 y por consiguiente tk = c14k+c22 k.
Pasando de nuevo a n en lugar de k encontramos T(n) = c1n2+c2n
Método Iterativo: Aquí utilizamos el método iterativo para resolver la ecuación de recurrencia
tn = tn-1 + 3, n>1 (1)
sujeta a la condición inicial t1=2.
Al reemplazar n con n-1 en (1) obtenemos
tn-1 = tn-2 + 3
si sustituimos esta expresión en (1) obtenemos
tn = tn-2 + 3 + 3
tn = tn-2 + 2(3 (2)
Al reemplazar n con n-2 en (1) obtenemos
tn-2 = tn-3 + 3
si sustituimos esta expresión para tn-2 en (2) obtenemos
tn = tn-3 + 3 + 2(3 = tn-3 + 3(3
En general, tenemos
tn = tn-k + k(3
Si hacemos k=n-1 en esta última expresión tenemos
tn = t1 + (n-1)(3
como t1=2, obtenemos la fórmula explícita
tn = 2 + 3((n-1)
Es importante que se haya notado que las soluciones generales que se proponen para una ecuación recurrente coinciden con las soluciones generales que hay que establecer para dar solución a una ecuación diferencial, hay que agregar incluso que si no hay condiciones iniciales entonces es infinito el número de valores a obtener por la sucesión.
Tarea docente 1: Población de venados
Vincular la aplicación de relaciones recursivas al crecimiento de una especie de animales que pueden estar en peligro de extinción.
En este problema se hace un uso de los contenidos abordados anteriormente. En este ejemplo el método iterativo es una opción viable para resolver la problemática, pero hay que tener algo en cuenta cuando se vaya a utilizar: el método iterativo se utiliza cuando el crecimiento de la función es fijo no que dependa de otro factor, es decir la función que estamos midiendo crece en un tamaño t (fijo) en el instante de tiempo t0, t1, tk
Suponga que la población de venados en una reserva es 1000 en el tiempo n=0 y que el aumento entre el tiempo n-1 y el tiempo n es un 10% del tamaño en el tiempo n-1. Escriba una relación de recurrencia y una condición inicial que defina la población de venados en el tiempo n y después resuelva la relación de recurrencia (Johnsonbaugh, 2018).
Sea dn la población de venados en el tiempo n. Se tiene la condición inicial d0=1000. El incremento del tiempo n-1 al tiempo n es dn-dn-1. Como este incremento es el 10% del tamaño en el tiempo n-1, se obtiene la relación de recurrencia
dn-dn-1= 0.1dn-1
Resolviendo la ecuación anterior mediante iteraciones se obtiene
dn= 1.1dn-1= 1.1(1.1dn-2) = (1.1)2(dn-2)= ··· = (1.1)nd0= (1.1)n1000.
Tarea docente 2: Otro problema de población de venados
Suponga que la población de venados del condado Rustic es 200 en el tiempo n=0 y 220 en el tiempo n=1, y que el incremento del tiempo n-1 al tiempo n es dos veces el incremento del tiempo n-2 al tiempo n-1. Escriba la relación de recurrencia y una condición inicial que define la población de venados en el tiempo n y después resuelva la relación de recurrencia (Johnsonbaugh, 2018).
d1= 200 d2= 220
El incremento del tiempo n-1 al tiempo n es dn-dn-1, y el incremento del tiempo n-2 al tiempo n-1 es dn-1-dn-2. Entonces se obtiene la relación de recurrencia dn-dn−1 = 2(dn-1-dn-2), que se escribe como dn= 3dn−1-2dn−2.La solución de la recurrencia anterior es dn= 180 + 20 · 2n
Tarea docente 3: Plantación de árboles
Vincular la aplicación de relaciones recursivas a la flora.
En una plantación hay 51 filas de árboles. Cada fila tiene dos árboles más que la anterior. La fila 26 tiene 57 árboles. ¿Cuántos árboles hay en la primera y en la última fila?
fn=fn-1+2 f26=57
Se sustituye n por n-1 y se obtiene
fn-1=fn-2 + 2 (**)
Se sustituye ** en la original y se obtiene
fn= fn-2 + 2 +2
Se sustituye n por n-2
fn-2= fn-3+2 (***)
Se sustituye la ecuación anterior y se obtiene
fn= fn-3+2+2+2= fn-3+6
Utilizando el método iterativo se obtiene de forma general
fn=fn-k+2k se sabe que n-k=26 → -k=26-n
Sustituyendo el valor de -k en la ecuación general se obtiene
fn=57+2(26-n)=109-2n → f0=109, f1=107, f2=105 y f49 =11 f50=9
→ f1=107, f2=105 y f50 =9 f51=7
Las soluciones obtenidas son correctas, algunos autores definen que el primer término de una sucesión es el elemento s0 en cambio otros plantean que es s1 por eso en el ejemplo anterior se propusieron las dos posibles formas en las que se pueden expresar los términos de una sucesión.
Otras tareas docentes
Estas pueden realizarse durante una clase o como actividades para el estudio independiente.
En marzo de 1976, la población mundial llegó a 4000 millones. Una revista predijo que con una tasa de crecimiento anual promedio de 1.8%, la población mundial sería de 8000 millones al cabo de 45 años. ¿Cómo se compara este valor con el que predice el modelo según el cual la tasa de crecimiento es proporcional a la población en cualquier momento?
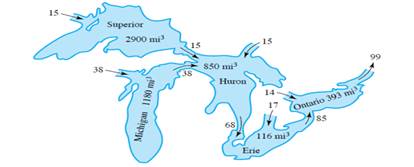
Establezca un modelo matemático para saber cuánto tiempo toma la limpieza de los grandes lagos. Apóyese en la Figura 1
Gracias a ciertos estudios realizados se sabe que la mosca del Mediterráneo crece en proporción al número presente en cada momento. Después de 2 horas de observación se forman 800 familias de la mosca y después de 5 horas se forman 2 000 familias. Encontrar: a. La ecuación que representa el número de familias en función del tiempo, y b. el número de familia que había al inicio.
La población de cierta ciudad aumenta proporcionalmente al número de habitantes que hay en un momento dado en ella. Si después de 5 años, la población se ha triplicado y después de 8 años es de 45 000 habitantes, hallar el número de ciudadanos que había inicialmente.
En el proceso de respiración absorbemos aire que contiene principalmente nitrógeno y oxígeno, y al exhalar despedimos bióxido de carbono. Se quiere purificar el ambiente de un salón donde se encuentran bailando un gran número de personas; para ello, se hace pasar una corriente de aire puro de 3 500 m3/h de aire al que llamaremos Qa1, y se hace salir 3 000 m3/h de aire contaminado (Qa2), con bióxido de carbono. A la concentración de bióxido de carbono por C f CO 2. Se sabe que el volumen del salón es de 10 000 m3 y que la concentración inicial de bióxido de carbono en el cuarto es de 0.1% del volumen de éste. Suponiendo que la densidad permanece constante, ¿cuál es la concentración de bióxido de carbono, ¿C f CO2, luego de 4 horas de haberse iniciado el baile? La concentración se expresa en g/m3.
La tasa de crecimiento de una población es proporcional al número de sus habitantes. Si después de 18 años la población se ha duplicado y después de 25 años la población es de 200000 habitantes, hallar:
En cierto zoológico se ha observado que la cantidad de animales aumenta proporcionalmente al número actual de dichos animales. Si después de 5 años su número se ha duplicado y después de 7 años el número de animales es 576, hallar el número de animales con que se contaba el día de la inauguración del zoológico.
Cierto hombre tiene una pareja de conejos en un lugar cerrado y desea saber cuántos se podrán reproducir en un año a partir de la pareja inicial, teniendo en cuenta que de forma natural tienen una pareja en un mes, y que a partir del segundo se empiezan a reproducir. Establezca una relación recurrente para el problema anterior y resuélvala. Intente definir una ecuación diferencial que solucione el mismo problema y compare los resultados.
Conclusiones
Las tareas docentes, en particular las tareas matemáticas, permiten el planteamiento y solución de problemas matemáticos-medioambientales, que contribuyen a la formación de una concepción científico - ambientalista en los estudiantes, principalmente los problemas prácticos, que requieren de la aplicación de conocimientos de ambas disciplinas, a la vez que desarrolla en ellos otras cualidades profesionales, necesarias para su desempeño laboral exitoso.
Una tarea matemática por sí sola no le permite al alumno comprender la esencia del proceso de solución de los problemas de la vida cotidiana, ni mucho menos llegar a conformar una visión más global del objeto de estudio, para ello se requiere de verdaderos sistemas de tareas docentes, que el profesor está en el deber de diseñar.