ARTÍCULO ORIGINAL

 

 

Modelos matemáticos para pronosticar parámetros reológicos de hidromezclas lateríticas

 

 

Mathematical models to predict rheological parameters of lateritic hydromixtures

 

 

 

Gabriel Hernández Ramírez¹, Arístides A. Legrá Lobaina¹, Beatriz Ramírez Serrano¹, Liudmila Pérez García²

 

¹Instituto Superior Minero Metalúrgico. Moa, Cuba [e-mail]
²Ing. Química. Doctora en Ciencias Técnicas. Profesora Auxiliar. Pedro Sotto Alba Moa Níquel SA. Moa, Cuba [e-mail]

 

 

---

RESUMEN

El presente trabajo tuvo como objetivo establecer modelos matemáticos que permitan el pronóstico de los parámetros reológicos de la pulpa laterítica a concentraciones de sólidos desde 35 % hasta 48 %, temperatura de la hidromezcla precalentada superior a los 82 °C y número de mineral entre 3 y 16. En el estudio se utilizaron cuatro muestras de pulpa laterítica en diferentes ubicaciones del proceso. Los resultados permitieron definir que las propiedades plásticas de la pulpa laterítica en las condiciones de este estudio se ajustan al modelo de Herschel-Bulkley para plásticos reales. Además, evidencian que para las condiciones de operación actuales, incluso para situaciones nuevas, los modelos matemáticos UPD tienen una mayor capacidad de predicción de los parámetros reológicos que los modelos matemáticos de mínimos cuadrados.

Palabras clave: hidromezclas lateríticas; parámetros reológicos; modelos matemáticos.

 

---

ABSTRACT

The present work had as objective to establish mathematical models that allow the prognosis of the rheological parameters of the lateritic pulp at concentrations of solids from 35% to 48%, temperature of the preheated hydromixture superior to 82 ° C and number of mineral between 3 and 16. Four samples of lateritic pulp were used in the study at different process locations. The results allowed defining that the plastic properties of the lateritic pulp in the conditions of this study conform to the Herschel-Bulkley model for real plastics. In addition, they show that for current operating conditions, even for new situations, UPD mathematical models have a greater ability to predict rheological parameters than least squares mathematical models.

Keywords: lateritic hydromixtures; rheological parameters; mathematical models.

---

 

 

 

1. INTRODUCCIÓN

En la industria del níquel de la región oriental de Cuba conocer el comportamiento reológico de las suspensiones de minerales lateríticos y su influencia en el proceso de lixiviación ácida es de vital importancia para lograr una explotación óptima de dicha tecnología. Cuando estas relaciones de influencia solo se conocen de manera general es necesario realizar nuevas caracterizaciones experimentales para determinar los vínculos específicos entre las propiedades de las hidromezclas lateríticas crudas.

Varios investigadores en el mundo han dedicado sus estudios al campo de la reología de polímeros (Mewis et al. 1989; Caram et al. 2006; McGuire, Addai y Bremmell 2006; Gomes y Marchese 2013; Li et al. 2016) y de emulsiones de petróleo (Ohtake, Hano y Takagi 1987; Pal y Masliyah 1990; Briceño et al. 1997; Briceño, Salager y Bertrand 2001; Rodríguez, Angulo y Falcón 2015; Vernáez et al. 2016). Otros han analizado el comportamiento reológico de suspensiones de minerales como bentonita (Bekkour, Leyama y Benchabane 2005; Işçi, Seniha y Güngör 2005), goethita (Blakey 2003) y lateritas procedentes de distintos yacimientos (Bhattacharya y Panda 1998; Larson 1999; Klein y Hallbom 2002; Blakey 2003; Pérez et al. 2010).

Estudios realizados en pulpas lateríticas cubanas han permitido determinar que para concentraciones inferiores al 18 % en peso de sólidos, las curvas de flujo prácticamente son independientes de su composición mineralógica y exhiben un comportamiento seudoplástico (Garcell, Díaz y Surís 1988; Avramidis y Turian 1991; Cerpa y Garcell 1998; Garcell et al. 1998; Garcell 2001; Izquierdo, Turro y Nikolaev 2001; Pérez 2004; Pérez  et al. 2010; Hernández, Pérez y Rodríguez 2016).

Sin embargo, para concentraciones de alrededor de 22 % hasta 45 % en peso de sólidos, la viscosidad aumenta dependiendo cada vez más de la mineralogía y en este caso el comportamiento reológico adquiere propiedades plásticas, pudiendo ajustarse en algunos casos al modelo de Bingham y en otros al de Bulkley–Herschel. Estas suspensiones lateríticas se comportan como flujos no newtonianos con plasticidad, debido a su carácter de materiales polidispersos, con un predominio de granulometría fina, con partículas menores de 0,045 mm.

Se destacan los resultados obtenidos por Pérez (2010) al obtener los modelos matemáticos que correlacionan los principales factores de influencia sobre el comportamiento reológico de las pulpas lateríticas. Los resultados obtenidos son válidos en el dominio de operación del proceso a temperatura ambiente, a niveles de concentración de sólidos entre 43 %, y 45 %, número de mineral entre 10 y 20, índice de estabilidad entre 0,03 y 0,12 y coeficiente de polidispersión entre 0,74 y 0,79. Estas limitantes no permiten establecer relaciones entre los factores que caracterizan las pulpas cruda y precalentada.

El presente trabajo tiene como objetivo establecer modelos matemáticos que permitan el pronóstico de los parámetros reológicos de la pulpa laterítica, a concentración de sólidos desde 35 % a 48 %, temperatura de la hidromezcla precalentada superior a 82 °C y número de mineral entre 3 y 16.

2. MATERIALES Y MÉTODOS

Para este trabajo se escogieron cuatro muestras de pulpa laterítica del proceso de lixiviación ácida en las siguientes ubicaciones: en la descarga del espesador A y D, en la línea de transferencia, y en la descarga de las bombas volumétricas. También se tomaron muestras de agua de reboso de los tanques de sedimentación para realizar las diluciones necesarias durante la preparación de soluciones, a diferentes concentraciones de sólidos.

2.1. Equipos y utensilios

Equipos: Viscosímetro HAAKE VT 550. Balanza técnica digital. Balanza secadora. Agitador mecánico con impelente mecánico. Plancha térmica. Bomba de agua.

Utensilios: Probetas de 500 ml. Beakers de 500 ml. Recipiente de 20 l. Jeringuillas de 20 ml. Frascos de 250 ml.

2.2. Preparación de las suspensiones minerales

Para la preparación de las suspensiones minerales se definieron las proporciones de sólido a ser evaluados: 37 %, 40 %, 43 %, 46 % y 48 %. Se tomaron muestras compósito (MC) de pulpa en tanquetas de 20 l. La Tabla 1 muestra los valores de porcentaje de sólido reportados por el control de operaciones de la planta.

Teniendo en cuenta que el porcentaje de sólido de pulpa inicial de cada muestra no fue el mismo, una vez tomadas las muestras se dejaron reposar para que sedimentaran, hasta lograr un 48 % de sólidos; el agua exudada se extrajo por decantación. En beakers de 500 ml se prepararon, de cada una de las muestras a partir de su dilución, cinco suspensiones en los cinco porcentajes definidos para este estudio.

2.3. Selección de variables

Las propiedades reológicas o variables dependientes que son de especial interés para obtener los modelos matemático son:

μ_a: viscosidad aparente de la suspensión, identificada como Y₁.

t₀: Esfuerzo cortante inicial, identificada como Y₂.

K: índice de consistencia, identificada como Y₃.

n: índice de flujo, identificada como Y₄.

Y las que constituyen respuestas cuando varían experimentalmente ciertas propiedades de la pulpa:

s: parámetro característico de la granulometría (coeficiente de polidispersión), identificada como X₁.

%S: contenido de sólido (porcentaje másico de sólidos en la pulpa), identificada como X₂.

pH, identificada por X₅.

Nrmin: Número mineral, identificada como X₄.

A partir de los datos obtenidos por Pérez (2010), se determinaron modelos lineales (r es el coeficiente de correlación) y se obtuvo, mediante pruebas de hipótesis, la validez del nivel de influencia de las variables independientes sobre las variables dependientes. Además, se consideró importante incorporar la variable independiente temperatura, denotada como X₃. Se han realizado muy pocos estudios acerca del efecto de la temperatura en las suspensiones de laterita, entre ellos están los realizados por Pérez (2004), Pérez y Garcell (2006) y Hernández, Rosa y Durán (2015). No se conocen referencias de investigaciones previas del comportamiento de los parámetros reológicos de la pulpa precalentada que es procesada en la planta de lixiviación a una temperatura superior a 82 ⁰C.

2.4. Mediciones reológicas

Para las mediciones reológicas se utilizó un viscosímetro rotacional marca HAAKE 550, al cual se le conectó una bomba de flujo para hacer recircular el agua a diferentes temperaturas para precalentar la pulpa.

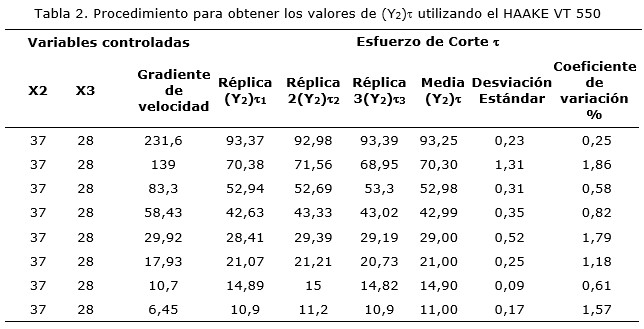
Para obtener los valores de esfuerzo de corte se midieron tres réplicas para cada valor de gradiente de velocidad y se determinaron las correspondientes medias aritméticas, desviación estándar y coeficiente de variación, que no excedió del 5% (Tabla 2).

2.5. Técnica de florescencia de rayos X para determinar la composición química

La composición química del mineral se determinó mediante análisis químicos, con los que se identifican 10 elementos; pero como en el proceso se emplea un parámetro denominado Número de Mineral (Nrmin) para predecir el comportamiento de la pulpa cruda en la sedimentación (que se determina por la ecuación 1), se decidió utilizarlo como variable representativa de la composición química en el diseño de experimentos.

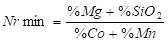 (1)

Se ha comprobado que cuando 7 < Nrmin < 14 la pulpa tiene buena sedimentación.

2.6. Análisis granulométrico de las muestras por analizador de tamaños

La determinación de las distribuciones granulométricas de las muestras se realizó mediante un analizador de tamaño de partículas del tipo Analysette 22 COMPACT, el cual permite obtener fracciones de partículas menores de 0,045 mm (325 mallas), que no pueden ser determinadas mediante el uso de tamices y que ejercen un efecto importante sobre el comportamiento de estas pulpas.

3. RESULTADOS Y DISCUSIÓN

3.1. Composición química de las suspensiones lateríticas

La Tabla 3 muestra la composición química y número de mineral de las muestras seleccionadas para el experimento.

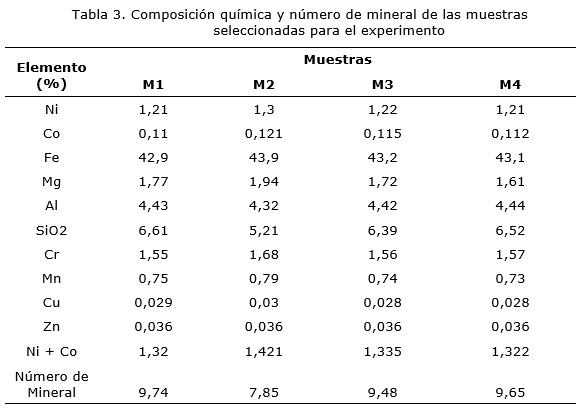
Como puede apreciarse, la pulpa posee un alto contenido de hierro, característica típica de las lateritas cubanas, en las que abundan los óxidos de este metal (Agyei 2006). En cada muestra todos los elementos se encuentran dentro de los dominios del proceso productivo y los parámetros óptimos para la operación de la planta.

3.2. Análisis granulométrico

Los resultados del análisis de distribución de tamaño de partículas minerales se asemejan a lo reportado por Pérez (2010), en cuanto a que: la pulpa cruda de laterita posee un 30 % de partículas mayores de 0,045 mm, existe un predominio de las fracciones finas de forma general y el D₈₀ se corresponde con el diámetro de partícula igual a 0,006872 mm, aproximadamente 7 µm. Todo ello indica que el 80 % de la muestra presenta un diámetro inferior a este valor, por tanto, las partículas más finas son mayoritarias y determinan la velocidad de sedimentación de este mineral, así como su comportamiento reológico; es decir, las partículas de todos estos materiales tienen un comportamiento propio de sistemas polidispersos.

Los resultados (Tabla 4) fueron ajustados al modelo de distribución granulométrica (Pérez 2010) y comprobados por Hernández, Pérez y Rodríguez (2016).

3.3. Resultados experimentales para el comportamiento reológico de la pulpa

Pulpa cruda

Luego de haber realizado las mediciones reológicas a las muestras de pulpa cruda en la línea de transferencia (M3), para los cinco porcentajes de sólidos evaluados y manteniendo constante la temperatura a 28^º C, se obtuvieron los valores de esfuerzos de corte y gradiente de velocidad representados en la Figura 1. La representación gráfica de los datos experimentales de gradiente de velocidad (g) contra esfuerzo de corte (t) permiten realizar el ajuste de los modelos reológicos.

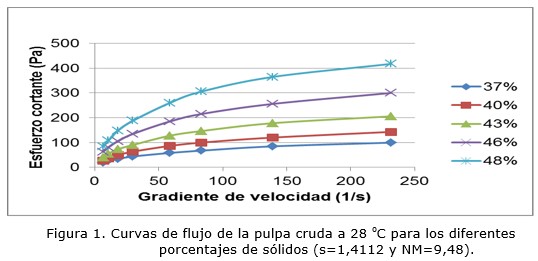
La Figura 1 describe el comportamiento típico de las suspensiones no newtonianas. A medida que aumenta la concentración de sólidos, los esfuerzos de corte (t) se incrementan, al igual que el valor de las viscosidades aparentes, para un valor fijo de gradiente de velocidad (g).

Mediante una aplicación informática se determinó la forma de la curva de flujo que fueron ajustados al modelo Herschel-Bulkley para plásticos reales, indicando la presencia de un esfuerzo de corte inicial (t₀), como se muestra en la Tabla 5.

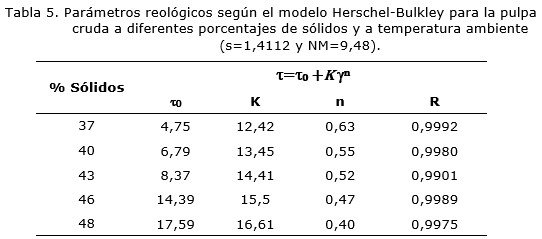
Los cambios en las constantes reológicas se produjeron tal y como se esperaba, pues los valores de esfuerzo de corte inicial y el índice de consistencia másico (K) aumentaron, mientras que los valores de índices de flujo (n) disminuyeron con el incremento de la concentración de fase sólida en la suspensión.

Pulpa precalentada

Se realizaron las mediciones reológicas de la muestra de pulpa precalentada tomadas en la descarga de la bomba de desplazamiento positivo (M4), a un porcentaje fijo; en este caso se escogió 40 % de sólidos por ser este el valor que se obtiene con más frecuencia en la pulpa precalentada bajo condiciones actuales de operación y a diferentes temperaturas (28 ^ºC, 40 ^ºC, 50 ^ºC, 60 ^ºC, 70 ^ºC, 80 ^ºC y 90 ^ºC), para analizar la influencia de la misma sobre los parámetros reológicos.

Al representar gráficamente la relación entre el esfuerzo cortante (t) y el gradiente de velocidad (g) se obtuvieron las curvas de flujo representadas en la Figura 2.

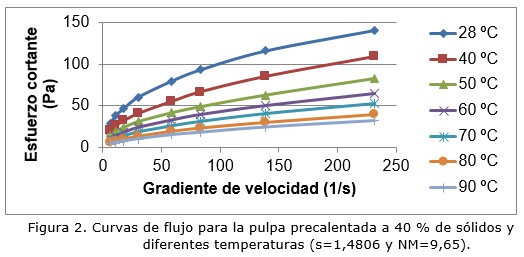
Las curvas obtenidas también describen el comportamiento típico de las suspensiones no newtonianas, ajustándose al modelo de Herschel-Bulkley para plásticos reales. Se observa que a medida que aumenta la temperatura, el esfuerzo cortante disminuye, al igual que la viscosidad del fluido.

Se confirma entonces que a altas temperaturas los valores de las propiedades plásticas de la pulpa laterítica tienden a disminuir, presentando esta un comportamiento menos viscoso, de ahí que los problemas de alta viscosidad que en ocasiones se presentan con las pulpas lateríticas son mayores a temperatura ambiente (Pérez 2004; Pérez et al. 2010). Los valores de los esfuerzos cortantes e índice de consistencia másica K disminuyeron; los valores del índice de flujo aumentaron, evidenciándose que a medida que aumenta la temperatura, la viscosidad aparente de la pulpa disminuye, y este es el comportamiento típico esperado en la mayoría de los líquidos y suspensiones.

3.4. Modelos matemáticos para pronósticos de parámetros reológicos

Teniendo en cuenta las frecuentes dificultades operativas para determinar el valor de coeficiente de polidispersión y considerando la menor influencia que tiene esta variable con respecto a las otras que refieren el comportamiento reológico de la pulpa, se desarrollaron modelos mínimos cuadrados (Tabla 6), que permiten explicar los valores de Y₁, Y₂, Y₃ y Y₄ en función de las variables físicas X₂, X₃ y X₄.

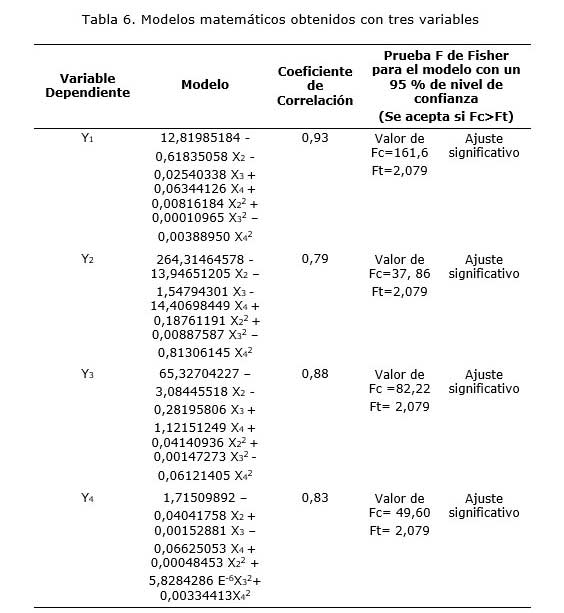
Dada la necesidad de obtener adecuados pronósticos de Y₁ para cualesquiera que sean los valores medidos de X₂, X₃, y X₄ en el proceso real de producción, se propone con estos fines el método denominado UPD (Legrá 2015; Legrá, Lamorú y Cala 2016), análogo al método de Funciones de Base Radial (Baxter 1992) y al de Kriging (Clark 2007).

Para esta modelación se tomaron los parámetros estándar del método: potencia de la distancia p=1, factor de suavización de la distancia δ=0 y deriva ε como la media aritmética de la variable dependiente.

A continuación se muestran los resultados de este modelo; nótese que para estimar la variable dependiente, en cada sumando aparece la distancia euclidiana  entre la coordenada P_i = (X_i2; X_i3; X_i4) de un dato y la coordenada del punto por donde se va a estimar P_e=(X₂; X₃; X₄):

Y₁= 0,02291d_1P + 0,00598d_2P + 0,00156d_3P - 0,01104d_4P - 3,27972E⁵d_5P + 0,003277d_6P + 0,004680d_7P - 0,009942d_8P - 0,010850d_9P - 0,001878d_10P + 0,0157583d_11P - 0,001864745d_12P - 0,00558d_13P - 0,000370d_14P + 0,0146953d_15P + 0,0464904_16P + 0,0427403d_17P + 0,0309242d_18P + 0,0306947d_19P + 0,0433756d_20P + 0,0224190d_21P + 0,1010392d_22P + 0,0408189d_23P + 0,0361621d_24P - 0,0143033d_25P + 0,0113755d_26P - 0,022953d_27P + 0,003928d_28P - 0,109138d_29P - 0,055350d_30P - 0,042753d_31P + 0,0173862d_32P + 0,00036220d_33P + 0,0129535d_34P + 0,0112266d_35P - 0,147509d_36P - 0,013894d_37P + 0,0994314d_38P + 0,1131460d_39P + 0,1377183d_40P + 0,1252790d_41P + 0,1523298d_42P + 0,0529902d_43P + 0,501153d_44P + 0,493034d_45P + 0,421942d_46P + 0,345063d_47P + 0,340137d_48P + 0,277950d_49P - 0,28388d_50P - 0,05902d_51P - 0,06165d_52P - 0,01044d₅₃P + 0,02950d_54P + 0,19371d_55P + 0,13971d_56P + 0,21732d_57P + 0,20404d_58P + 0,32240d_59P + 0,29986d_60P + 0,27537d_61P + 0,31414d_62P + 0,39228d_63P - 0,14098d_64P - 0,16935d_65P - 0,00838d_66P + 0,235621d_67P + 0,270722d_68P + 0,118497d_69P + 0,175142d_70P + 0,134687d_71P + 0,001575d_72P - 0,10611d_73P - 0,11170d_74P - 0,14496d_75P - 0,13518d_76P - 0,15778d_77P - 0,05125d_78P - 0,47841d_79P - 0,47512d_80P - 0,40792d_81P - 0,32918d_82P - 0,31875d_83P - 0,25990d_84P + 0,233632d_85P - 0,01020d_86P - 0,00146d_87P - 0,03745d_88P - 0,06595d_89P - 0,22710d_90P - 0,16415d_91P - 0,15925d_92P - 0,15466d_93P - 0,26406d_94P - 0,24687_95P - 0,24254d_96P - 0,27726d_97P - 0,38331d_98P + 0,054843d_99P + 0,111264d_100P - 0,02427d_101P - 0,29567d_102P - 0,28800d_103P - 0,14374d_104P - 0,19318d_105P + 0,01414d_106P - 0,00508d_107P - 0,01122d_108P - 0,02114d_109P - 0,00813d_110P + 0,003161d_111P - 0,0041646d_112P - 0,03085d_113P - 0,05217d_114P - 0,03271d_115P - 0,02189d_116P - 0,01566d_117P - 0,028932d_118P - 0,01887d_119P + 0,12856d_120P + 0,10959d_121P + 0,07644d_122P + 0,06466d_123P + 0,03138d_124P + 0,03127d_125P + 0,02385735d_126P + 0,02481d_127P + 0,05613d_128P + 0,04440d_129P + 0,00398d_130P + 0,04442d_131P - 0,02815d_132P - 0,00116d_133P - 0,06832d_134P - 0,06992d_135P - 0,09058d_136P - 0,02044d_137P - 0,08222d_138P + 0,001162d_139P - 0,00495d_140P + 0,58325

3.5. Análisis de los resultados

Tiene especial interés demostrar la sensibilidad de todo el procedimiento para la obtención de los modelos y para ello se comprobó, a partir de datos medidos en la etapa experimental, que cambios pequeños en los datos de entrada producen cambios de igual escala en los pronósticos hechos.

La comprobación del modelo mínimo cuadrado y modelo UPD para el pronóstico de la viscosidad aparente (Y₁) se muestran en la Tabla 7.

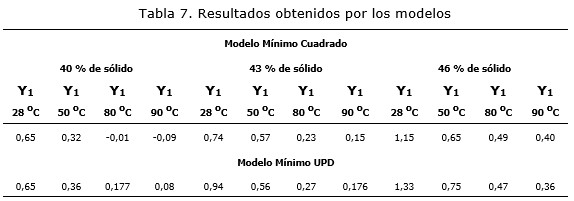
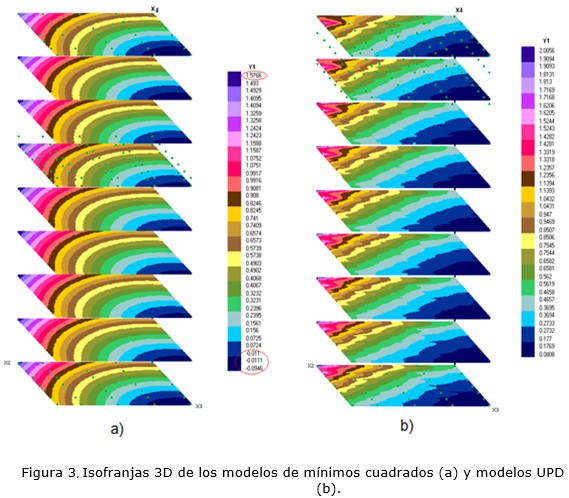
Los modelos de mínimos cuadrados presentan inconsistencias predictivas cuando los valores de las variables independientes se alejan suficientemente de los rangos de los datos y, en algunos casos, se obtienen valores inadecuados; para altas temperaturas los valores de viscosidad aparente son negativos.

En la Figura 3 se muestran isofranjas 3D de los dos modelos que evidencia la capacidad de pronósticos de los modelos UPD.

4. CONCLUSIONES

· De acuerdo con los resultados de los experimentos reológicos la pulpa laterítica cruda y precalentada presenta propiedades plásticas, ajustándose a un modelo de Herschel-Bulkley para plásticos reales.

· Los modelos matemáticos desarrollados permiten modelar y calcular los parámetros reológicos: viscosidad aparente, esfuerzo cortante inicial, índice de consistencia e índice de flujo.

· Se demuestra la capacidad de pronósticos de los modelos UPD para variables reales del proceso productivo.

5. REFERENCIAS

Avramidis, S. y Turian, R. M. 1991: Yield Stress of Laterite Suspensions. Journal of Colloid and Interface Science 143(1): 54.

Baxter, B. 1992: The Interpolation Theory of Radial Basis Functions. Tesis doctoral. University of Cambridge.

Bekkour, K. M.; Leyama, A. y Benchabane, O. 2005: Time-dependent rheological behavior of bentonite suspensions: An experimental study. Journal of Rheology 49(6): 1329-1345.

Bhattacharya, I. N. y Panda, P. 1998: Rheological behaviour of nickel laterite suspensions. International journal of mineral processing 53(4): 251-263.

Blakey, B. C. 2003: Characterizing the rheology of laterite slurries. International journal of mineral processing 70(1): 23-39.

Briceño, M.; Salager, J. y Bertrand, J. 2001: Influence of the dispersed phase viscosity on the mixing of concentrated oil-in-water emulsions in the transition flow regime. In: International Symposium on Mixing in Industrial Processes – ISMIP4. Toulouse, Francia.

Briceño, M. I.; Ramirez, M.; Bullón, J. y Salager, J. 1997: Customizing Drop Size Distribution to Change Emulsion Viscosity. In: 2nd World Congress on Emulsion CME2. Francia.

Caram, Y.; Bautista, F.; Puig, J. E. y Manero, O. 2006: On the rheological modeling of associative polymers. Rheologica acta 46(1): 45-57.

Cerpa, A. y Garcell, L. 1998: Propiedades superficiales y reológicas de suspensiones minerales lateríticas. En: Metalurgia 98. La Habana.

Clark, I. Y. H. W. 2007. Practical geostatistics. Ecosse North America Llc., Kinkos, Westerville, Ohio USA.

Garcell, L. 2001: Flujo por tuberías de suspensiones minerales no newtonianas. Monografía. Universidad de Oriente.

Garcell, L.; Díaz, L. y Surís, G. 1988: Transferencia de cantidad de movimiento, calor y masa. Pueblo y Educación, La Habana.

Garcell, L.; Morales, M. P.; Andres-Verges, M.; Tartaj, P. y Serna, C. J. 1998: Interfacial and Rheological Characteristics of Maghemite Aqueous Suspensions. Journal of Colloid and Interface Science 205(2): 470-475.

Gomes, M. y Marchese, T. 2013: Ajuste de Modelos Reológicos Mecânicos no Creep de Polipropileno, Poliestireno e Policarbonato: Comparação com o MEF. Revista Iberoamericana de Polímero 14(2): 65-82.

Hernández, G.; Pérez, L. y Rodríguez, K. 2016: Influencia de los parámetros reológicos de la pulpa de mineral laterítico en la eficiencia del sistema de bombeo de hidromezclas. In: 3er Congreso Internacional de Minería y Metalurgia. Matanzas, Cuba.

Hernández, G.; Rosa, Y. y Durán, C. 2015: Influencia de la temperatura del fluido en la eficiencia energética de los sistemas de bombeos. En: CINAREM 2015. Instituto Superior Minero Metalúrgico de Moa, Holguin.

Işçi, S. F.; Seniha, Ö. y Güngör, N. 2005: Investigation of rheological and colloidal properties of bentonitic clay dispersion in the presence of a cationic surfactant. Progress in Organic Coatings 54(1): 28-33.

Izquierdo, R.; Turro, A. y Nikolaev, A. 2001: Hidrotransporte del mineral laterítico en régimen estructural. Minería y Geología 18(2): 53-59.

Klein, A. y Hallbom, D. 2002: Modifying the rheology of nickel laterite suspensions. Minerals Engineering 15(10): 745-749.

Larson, R. G. 1999: The Structure and Rheology of Complex Fluids. Vol. 150. Oxford University Press, New York.

Legrá, A. A. 2015: Método UPD-L para estimar valores de una variable geominera medidos en un conjunto de puntos de Rn. Minería y Geología 31(1): 1-12.

Legrá, A. A.; Lamorú, A. y Cala, H. A. 2016: Evaluación de modelos de variables geo-tecnológicas en un bloque de un yacimiento laterítico cubano: Quinta parte: Optimización combinatoria del Método UPD. Minería y Geología 32(4): 33-48.

Li, Z.; Wang, J.; Pérez-Camargo, R.; Müller, A. J.; Zhang, B.; Grayson, S. M. y Hu, W. 2016: Non-monotonic molecular weight dependence of crystallization rates of linear and cyclic poly(epsilon-caprolactone)s in a wide temperature range. Polymer International 65(9): 1074-1079.

Mcguire, M. J.; Addai, J. y Bremmell, K. 2006: The effect of polymer structure type, pH and shear on the interfacial chemistry, rheology and dewaterability of model iron oxide dispersions. Colloids and Surfaces A: Physicochemical and Engineering Aspects 275(1): 153-160.

Mewis, J.; Frith, W.; Strivens, T. y Russel, W. 1989: The Rheology of Suspensions Containing Polymerically Stabilized Particles. AIChE Journal 35(3): 415-422.

Ohtake, T.; Hano, K. y Takagi, F. 1987: Effects of viscosity on drop diameter of w/o emulsion dispersed in a stirred tank. Journal of Chemical Engineering of Japan 20(5): 443-447.

Pal, R. y Masliyah, J. 1990: Rheology of oil in water emulsions with added solids. The Canadian Journal of Chemical Engineering 68(1): 24-28.

Pérez, L. 2004: Efecto de la temperatura y de la distribución de tamaño de las partículas sobre la correlación entre las propiedades reológicas y coloidequímicas de las suspensiones lateríticas. Tesis de maestría. Universidad de Oriente, Santiago de Cuba.

Pérez, L. y Garcell, L. 2006: Influencia de la distribución de tamaño de las partículas y de la temperatura sobre la reología de suspensiones lateríticas. Tecnología Química 26(1).

Pérez, G. L. 2010: Modelo matemático que correlaciona los principales factores de influencia sobre el comportamiento reológico de las pulpas lateríticas. Tesis doctoral. Universidad de Oriente, Santiago de Cuba.

Pérez, L.; Garcell, L.; Rojas, A. y Simoes, R. 2010: Mineralogía y reología de suspensiones minerales del proceso de lixiviación ácida a presión en Moa. Minería y Geología 26(4): 16-35.

Rodríguez, T. H.; Angulo, H. J. y Falcón, J. 2015: Comportamiento reológico de las emulsiones empleando productos de la pirolisis. Tecnología Química 35(3): 412-423.

Vernáez, O.; García, A.; Castillo, F.; Ventresca, M. L. y Müller, A. J. 2016: Oil-based self-degradable gels as diverting agents for oil well operations. Journal of Petroleum Science and Engineering 146: 874-882.

 

 

 

Recibido: 17/02/2017
Aprobado: 13/09/2017

 

 

 

Gabriel Hernández Ramírez, Ing. Eléctrico. Máster en Electromecánica. Profesor Auxiliar, Instituto Superior Minero Metalúrgico. Moa, Cuba [e-mail]