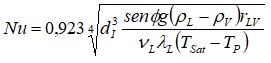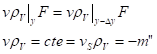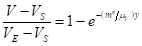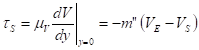INTRODUCCIÓN
En la actualidad, en los aerocondensadores (ACC) la condensación se desarrolla en el interior de tubos, lo cual complica la determinación de los coeficientes de transferencia de calor, debido a que la velocidad del vapor y la rapidez de la acumulación de líquido. En el interior de los tubos el vapor es confinado, y condensa a medida que avanza a lo largo del mismo. El flujo de vapor resulta orientado y su velocidad puede ser muy alta (más de 100 m/s), por lo tanto, la fricción en la interface vapor-líquido es apreciable (Boyko y Kruzhilin 1967; Zhang et al. 2015).
Si las direcciones del flujo de vapor y condensado coinciden en sentido descendente, la fricción produce una aceleración del condensado, adelgazando la película y aumentando el coeficiente de transmisión superficial del calor. En caso contrario, el coeficiente medio de transferencia de calor se verá penalizado por esta razón. Un incremento de la velocidad del vapor puede provocar el arrastre de la película y su separación parcial de la pared, incrementando la transmisión de calor, por lo tanto, en el interior de tubos, esta puede depender del efecto dinámico del vapor sobre la película de condensado (Song; Cui y Liu 2017; Camaraza-Medina et al.2017; Chen et al. 2019).
Este efecto se manifiesta de formas distintas, según sea la dirección de la gravedad y de la fricción, lo cual no sólo está determinada por la posición del tubo en el espacio, sino también por la dirección del flujo de vapor, hacia arriba o hacia abajo, en tubos inclinados o verticales (Mondal y Field 2018; Rabiee et al. 2018).
En la literatura, la evaluación de la condensación en ACC es dividido en cuatro intervalos, lo cual complica el análisis, sobre todo en sistemas múltiples de paneles ACC, debido a la influencia ejercida por la longitud de los tubos, generando dos o más intervalos de condensación en un mismo tubo (Camaraza-Medina et al. 2018).
Este inconveniente es una limitante actual en las plantas de potencia que utilizan ACC, pues para garantizar altas potencias de salida, es requerido también evacuar elevados flujos de calor en condensadores, siendo requerido el uso de celdas ACC múltiples, haciendo la evaluación termo-hidráulica del ACC una tarea compleja y engorrosa (Medina, Fonticiella y Morales 2017; Camaraza-Medina; Cruz-Fonticiella y Garcia-Morales 2019; Camaraza-Medina et al. 2020).
En la actualidad, no se dispone de un método unitario que permita estimar los coeficientes de transferencia de calor por condensación a lo largo del tubo. La práctica ingenieril utilizada es dividir en zonas, y posteriormente sumar los coeficientes individuales obtenidos, sin embargo, este procedimiento introduce errores de ponderación y sumas, lo cual reduce el nivel de predicción e incrementa la incertidumbre en la evaluación térmica del ACC (Kim y Mudawar 2013; Cttani; Bozzoli y Raineri 2017; Cheng et al. 2019).
En el ACC, como agente refrigerante es utilizado el aire ambiente, lo cual reduce apreciablemente los coeficientes globales de transferencia de calor. La recirculación de aire caliente y el efecto del viento sobre la instalación son elementos desfavorables que influyen de forma negativa en el proceso de condensación, afectando en muchos casos las magnitudes de los coeficientes globales. Los métodos disponibles en la actualidad no contemplan la influencia ejercida sobre el desempeño térmico del ACC por la temperatura ambiente y la velocidad del viento, siendo esto otra limitante para la evaluación térmica de este.
En trabajos anteriores fueron presentados algunos métodos para la estimación de los coeficientes de transferencia de calor durante la condensación pelicular confinada en ACC; sin embargo, al extender su uso a instalaciones ACC que operen en zonas tropicales T_0≥30℃, la correlacion de valores medidos con los computados por estos métodos arrojan desviaciones medias de ±25%, lo cual reduce la confiabilidad de su aplicación para condiciones ambientales más agresivas y con mayor contenido de humedad relativa (Cancan et al. 2017; Medina et al. 2018).
Por tanto, el objetivo principal de este trabajo es obtener una metodología única, que permita solventar estas limitaciones y cuyo error de ajuste sea inferior a los computados con el empleo de los métodos disponibles en la actualidad (25 %), siendo válido, además, en las cuatro regiones conocidas. Para este propósito son utilizados un grupo de datos experimentales disponibles, obtenidos a partir de comunicación directa con especialistas de prestigio en el área de acción a nivel internacional, así como valores reportados en trabajos elaborados con similar propósito.
MATERIALES Y MÉTODOS
Criterios de diferenciación del flujo de condensación dominante
La obtención del coeficiente medio de transferencia de calor, durante la condensación de vapor de agua en el interior del ACC, se efectúa considerando a tal efecto, que el vapor posee una velocidad despreciable. Esta expresión (1) viene dada por Medina y demás investigadores (2018):
Donde: 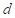 es el diámetro interno de los tubos, en m.
es el diámetro interno de los tubos, en m.  es la aceleración de la gravedad, en m/s2.
es la aceleración de la gravedad, en m/s2.  es el ángulo de inclinación de los tubos con respecto a la horizontal, en grados.
es el ángulo de inclinación de los tubos con respecto a la horizontal, en grados. 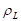 es la densidad del líquido saturado, en
es la densidad del líquido saturado, en 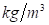 .
.  es la densidad del vapor saturado, en
es la densidad del vapor saturado, en  .
.  es el calor latente, en
es el calor latente, en 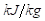 .
. 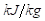 es la viscosidad cinemática del líquido, en
es la viscosidad cinemática del líquido, en 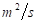 .
.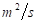 es la conductividad térmica del líquido, en
es la conductividad térmica del líquido, en  .
.  es la temperatura de saturación, en
es la temperatura de saturación, en 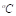 .
. 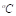 es la temperatura de la pared de los tubos, en
es la temperatura de la pared de los tubos, en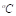 .
.
Sin embargo, las diversas situaciones operativas hacen que el criterio de flujo dominante en el interior de los tubos del ACC sea variable, razón por la cual es necesario determinar cuál es el criterio dominante para posteriormente proceder al análisis de caso. Un criterio muy empleado para solucionar esta problemática es dado por Medina et al. (2018), el cual se basa en la combinación de los dos criterios adimensionales siguientes (2) y (3):
Velocidad adimensional
Criterio adimensional de Crosser
En las ecuaciones (2) y (3), se cumple que x es la calidad del vapor que sale de turbina,  es la viscosidad dinámica del líquido a la presión de saturación, en Pa.s.
es la viscosidad dinámica del líquido a la presión de saturación, en Pa.s.  es la viscosidad dinámica del vapor a la presión de saturación, en Pa.s.
es la viscosidad dinámica del vapor a la presión de saturación, en Pa.s.  es el caudal másico del flujo de vapor, en kg/s.
es el caudal másico del flujo de vapor, en kg/s.  es el diámetro interno equivalente de los tubos en los cuales condensa el vapor, en m.
es el diámetro interno equivalente de los tubos en los cuales condensa el vapor, en m.
Los resultados obtenidos con el uso de las relaciones (2) y (3) permiten identificar el criterio de flujo dominante, empleando para ello los identificativos proporcionados en la Tabla 1. Tal como se puede comprobar en la referida tabla, el proceso de condensación de vapor de agua en el interior de los tubos de un sistema ACC es sumamente complejo, pues se forman varias zonas desde la entrada del vapor hasta la formación del líquido subenfriado.
Sería conveniente disponer inicialmente de las características fundamentales de cada zona de flujo así como de la expresión más aceptada y difundida en la literatura para la determinación del coeficiente medio de transferencia de calor en la misma.
Flujo estratificado-ondulado: Cuando el vapor posee una velocidad media o baja, la transferencia de calor convectiva en el líquido estratificado que se encuentra almacenado en el fondo del tubo puede que no sea despreciable, en segundo lugar el flujo axial de vapor puede interferir en la velocidad y en la transferencia de calor de la película alrededor de la pared del tubo. En el trabajo de Medina et al. (2018) fue estudiada detalladamente esta zona, siendo reportado adicionalmente que el régimen de flujo estratificado- ondulado se hace presente en el interior de un tubo cuando se cumpla que 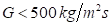 ,
,  y
y  .
.
El término 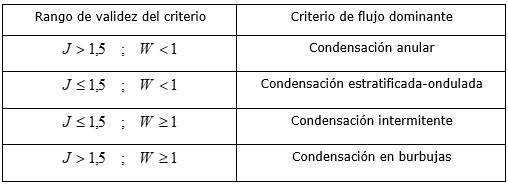 es el número modificado de Froude, el cual viene dado por (4):
es el número modificado de Froude, el cual viene dado por (4):
En la ecuación (4) el número de Reynolds para el estado líquido 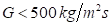 y el número de Galileo
y el número de Galileo 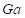 son determinados mediante las siguientes expresiones (5) y (6):
son determinados mediante las siguientes expresiones (5) y (6):
Finalmente, el valor numérico de las constantes A y B presentes en la expresión (4) son dependientes del número de Reynolds para el estado líquido 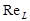 . Esta dependencia es mostrada en la Tabla 2.
. Esta dependencia es mostrada en la Tabla 2.
Mientras que el coeficiente de transferencia de calor medio en esta zona es dependiente de tres factores, los cuales son:
Coeficiente de transferencia de calor para la porción de vapor (7)
En la ecuación (7) se cumple que 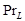 es el número adimensional de Prandtl para el estado líquido.
es el número adimensional de Prandtl para el estado líquido.  es el calor específico del estado líquido, en
es el calor específico del estado líquido, en 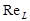
Ángulo de barrido de la porción de vapor (8) (véase la Figura 1)
Coeficiente de transferencia de calor para la porción líquida (9)
Las constantes numéricas C y D usadas en la ecuación (9) son resumidas en la Tabla 3.
Los resultados obtenidos con el empleo de las ecuaciones (7), (8) y (9) son combinados para obtener el coeficiente de transferencia de calor total mediante la siguiente expresión (10):
La expresión (10) es correlacionada con un total de 383 muestras experimentales disponibles, encontrándose que esta se ajusta con un error medio de 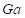 en el 79,4 % de los datos experimentales disponibles.
en el 79,4 % de los datos experimentales disponibles.
Flujo en niebla-anular: Este tipo de flujo se presenta cuando la velocidad del vapor es elevada, por lo que los efectos gravitacionales pueden ser ignorados, mientras que el condensado se deposita en una capa delgada anular alrededor de la pared del tubo, sin presencia de estratificación. Una parte significativa de la mayoría de los condensadores opera bajo las condiciones de este régimen de flujo.
De todos los modelos conocidos, es la ecuación de Chato el de mayor aceptación y uso en los sistemas ACC que operan en la zona anular. Esta queda dada por (11):
En esta zona los modelos de flujo laminar predicen valores bajos del coeficiente de transferencia de calor medio, por lo que deben ser empleados en este caso modelos turbulentos. El modelo de Chato (11) es expresado en función del número local de Nusselt, por lo tanto, deben ser integradas sobre toda la longitud del tubo en función de encontrar el coeficiente medio de transferencia de calor, de forma que (12):
Un inconveniente en la ecuación (12) radica en el hecho que debe ser conocida la dependencia de la calidad del vapor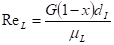 en la posición axial . Esto normalmente se soluciona subdividiendo la longitud total en un número de subelementos de longitud
en la posición axial . Esto normalmente se soluciona subdividiendo la longitud total en un número de subelementos de longitud 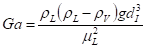 desde el comienzo del proceso de condensado, o sea de entrada a salida del tubo, usando el coeficiente local de transferencia de calor para cada subelemento (normalmente se toman cuatro elementos para alcanzar una precisión media). Si se asume que la calidad del vapor varia linealmente, lo cual desafortunadamente no ocurre en muchos casos) entonces el coeficiente de transferencia de calor puede ser determinado aproximadamente tomando la calidad del vapor como
desde el comienzo del proceso de condensado, o sea de entrada a salida del tubo, usando el coeficiente local de transferencia de calor para cada subelemento (normalmente se toman cuatro elementos para alcanzar una precisión media). Si se asume que la calidad del vapor varia linealmente, lo cual desafortunadamente no ocurre en muchos casos) entonces el coeficiente de transferencia de calor puede ser determinado aproximadamente tomando la calidad del vapor como 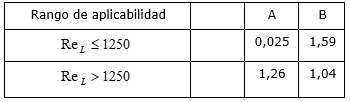 en las expresiones para la determinación del coeficiente de transferencia de calor local.
en las expresiones para la determinación del coeficiente de transferencia de calor local.
Una solución aproximada para este problema fue propuesta por Medina y demás investigadores (2018), quienes reportan a partir de un total de 813 mediciones efectuadas en laboratorio, que el comportamiento de la variación de la calidad del vapor presenta un comportamiento parabólico siempre que se cumpla en la entrada del tubo que 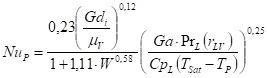 . Esta curva presenta una desviación de aproximadamente un
. Esta curva presenta una desviación de aproximadamente un 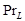 , siendo descrita mediante la siguiente expresión (13):
, siendo descrita mediante la siguiente expresión (13):
En la expresión (13) se cumple que 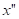 es la calidad del vapor en cualquier porción del tubo.
es la calidad del vapor en cualquier porción del tubo.  es la longitud de la sección analizada del tubo, en m.
es la longitud de la sección analizada del tubo, en m.  es la longitud total del tubo, en m.
es la longitud total del tubo, en m.  es la calidad del vapor a la entrada del tubo. Otra alternativa de solución es el empleo de los métodos numéricos.
es la calidad del vapor a la entrada del tubo. Otra alternativa de solución es el empleo de los métodos numéricos.
Flujo intermitente: Se presenta durante la condensación en tubos cuando la velocidad del vapor es demasiado baja (menor de 0,5 m/s) el flujo puede ser dominado por las fuerzas gravitacionales y puede ocurrir la estratificación del condensado, o sea, el condensado forma una película delgada en las pared de la porción superior del tubo y drena por la periferia de este por el efecto de la fuerzas gravitatorias hacia el fondo del tubo donde se une al condensado que fluye axialmente debido al esfuerzo cortante de la corriente fluida.
En la literatura conocida no se disponen de muchos trabajos sobre este tipo de criterio de condensación, y en todos los casos la más recomendada es la expresión (14). Esta correlaciona con una desviación máxima del 28 % en el 80,1 % de las muestras. En la literatura conocida no se disponen de muchos trabajos sobre este tipo de criterio de condensación, y en todos los casos la más recomendada es la expresión (14). Esta correlaciona con una desviación máxima del 28 % en el 80,1 % de las muestras.
Flujo en burbujas: Este régimen de flujo de condensado aparece cuando en el interior del tubo ya la mayor parte del contenido de este es líquido subenfriado; sin embargo, quedan aún burbujas individuales, las cuales colapsan y son controladas a la vez por la inercia del líquido y por la transferencia de calor, dependiendo en lo fundamental del grado de subenfriamiento del líquido.
Una de las expresiones más conocidas y recomendadas para este tipo de flujo es la ecuación de Jaster-Kosky, la cual viene dada por (15):
La expresión (15) correlaciona medianamente con datos experimentales disponibles, con una desviación máxima del 35 % en el 78,1 % de las muestras disponibles.
RESULTADOS
Validación experimental de un modelo único para la condensación en sistemas ACC
Tal como fue mostrado en el epígrafe anterior el estudio del proceso de transferencia de calor por condensación en sistemas ACC se torna complejo por la cantidad de elementos a considerar, así como el elevado número de expresiones involucradas en el estudio.
Sería razonable disponer de una expresión única que permita evaluar el coeficiente de transferencia de calor en cualquiera de las zonas y cuyos resultados ronden el entorno de precisión obtenido con el empleo de los actuales métodos, los cuales no fueron desarrollados para el uso exclusivo en sistemas ACC, razón principal de la falencia en muchos casos de los métodos disponibles en la actualidad.
La correlación de las cantidades experimentales disponibles permite disponer de una función única para la evaluación de la transferencia de calor por condensación, la cual responde a la siguiente expresión (16):
En la ecuación (16)
 es el número de Nusselt, determinado para la porción correspondiente al flujo de calor en medios de simple fase. El mismo se obtiene a partir de la siguiente expresión (17):
es el número de Nusselt, determinado para la porción correspondiente al flujo de calor en medios de simple fase. El mismo se obtiene a partir de la siguiente expresión (17):
Donde (18):
Los datos experimentales empleados en la generalización y desarrollo de la expresión (16) son resumidos en la Tabla 4, siendo ampliamente discutidos en (Medina et al. 2018). En la Figura 2 se muestra la correlación de datos experimentales con la ecuación (16), en el eje de las y es graficado el logaritmo decimal del cociente de los coeficientes peliculares calculados con el empleo de las ecuaciones (16) y (17) mientras que por el eje de las x se grafica el parámetro de Shah, el cual queda dado por (19):
Análisis del arrastre ocasionado por velocidades elevadas del vapor
Las expresiones brindadas con anterioridad son válidas solo si el arrastre del vapor es despreciable o insignificante. Esta suposición es adecuada en los ACC cuando la velocidad del vapor no sobrepasa los 50 m/s. Para velocidades superiores del flujo de vapor no puede ser ya ignorado el efecto del arrastre sobre la película líquida.
Para tener en cuenta el efecto del arrastre sobre la película líquida, es necesario incluirla influencia de esfuerzo cortante sobre la superficie del líquido, o sea (20):
En la ecuación (20) se cumple que  es el coeficiente de arrastre medio y
es el coeficiente de arrastre medio y  es la velocidad de la corriente libre, en
es la velocidad de la corriente libre, en 
Dos expresiones apropiadas aparentemente para la determinación de 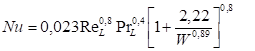 pudiesen ser las soluciones de Blasius para la capa límite laminar y la capa límite turbulenta, sin embargo, existe un problema adicional, y es que estas dos expresiones solo son válidas para una pared impermeable, mientras que la superficie del líquido tiene una componente normal de la velocidad debida a la condensación. En muchos textos de mecánica de fluidos se diría que en este caso hay presencia de succión en la superficie; en problemas típicos de condensación la velocidad de la succión es relativamente grande y hace que el espesor de la capa límite se vuelva casi constante muy cerca del borde inicial, y la velocidad del vapor
pudiesen ser las soluciones de Blasius para la capa límite laminar y la capa límite turbulenta, sin embargo, existe un problema adicional, y es que estas dos expresiones solo son válidas para una pared impermeable, mientras que la superficie del líquido tiene una componente normal de la velocidad debida a la condensación. En muchos textos de mecánica de fluidos se diría que en este caso hay presencia de succión en la superficie; en problemas típicos de condensación la velocidad de la succión es relativamente grande y hace que el espesor de la capa límite se vuelva casi constante muy cerca del borde inicial, y la velocidad del vapor  es, en esencia, solo función de
es, en esencia, solo función de  .
.
Esto puede ser resuelto parcialmente si es empleado el modelo elaborado por Couette para flujo laminar, puede ser aplicado para determinar los esfuerzos cortantes que actúan sobre una capa límite sujeta a un fuerte esfuerzo de succión (Figura 3).
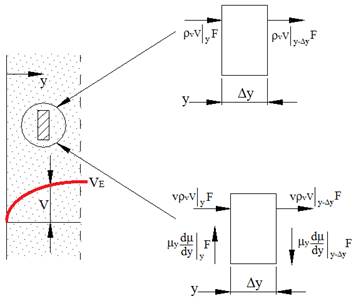
Figura 3 Problema modelo y volúmenes elementales para el análisis del efecto de la velocidad del vapor sobre el intercambio térmico.
La velocidad de la corriente libre 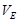 y la velocidad superficial es
y la velocidad superficial es 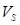 , la cual se supone independiente de la distancia
, la cual se supone independiente de la distancia 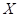 . De hecho
. De hecho 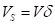 aumenta con
aumenta con 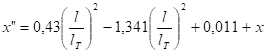 en el problema real de condensación en película, sin embargo, como por el momento solo se han considerado situaciones en las que
en el problema real de condensación en película, sin embargo, como por el momento solo se han considerado situaciones en las que 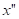 , además el error provocado por esta suposición es pequeño. En la Figura 3 se muestra un volumen de control elemental de espesor
, además el error provocado por esta suposición es pequeño. En la Figura 3 se muestra un volumen de control elemental de espesor  y área
y área 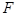 , situado dentro de la capa límite de vapor. La ley de conservación de la masa implica que (21):
, situado dentro de la capa límite de vapor. La ley de conservación de la masa implica que (21):
En la ecuación (21) se toma como positivo el valor de la velocidad de condensación  . La segunda ley de Newton implica que la suma de las fuerzas que actúan sobre el volumen sea igual a la velocidad de cambio de la cantidad de movimiento del fluido que pasa a través de dicho volumen. En dirección
. La segunda ley de Newton implica que la suma de las fuerzas que actúan sobre el volumen sea igual a la velocidad de cambio de la cantidad de movimiento del fluido que pasa a través de dicho volumen. En dirección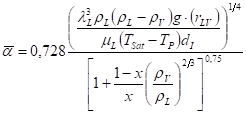 se cumple que (22):
se cumple que (22):
Si en la ecuación (22) se sustituye el término  de la relación (21), se divide entre
de la relación (21), se divide entre 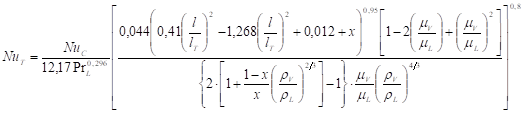 y posteriormente se hace
y posteriormente se hace  , de estas operaciones se obtiene (23):
, de estas operaciones se obtiene (23):
La relación (23) es la ecuación diferencial que rige el comportamiento de la velocidad  del vapor cuando su viscosidad es constante. Las condiciones de contorno apropiadas para este caso son (24):
del vapor cuando su viscosidad es constante. Las condiciones de contorno apropiadas para este caso son (24):
Reordenando la ecuación diferencial (23) e integrando se llega a (25):
Evaluando las constantes de integración en (25) a partir de las condiciones de contorno se obtiene la siguiente expresión para el perfil de velocidad (26):
Por lo tanto, el esfuerzo cortante en la superficie de la película resulta ser (27):
Así, en el límite de las succiones fuertes, el esfuerzo cortante que el vapor ejerce sobre la película de líquido es simplemente la cantidad de movimiento cedido por la condensación de vapor al desacelerar de la velocidad de corriente libre 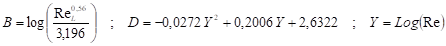 a la velocidad de la superficie de la película
a la velocidad de la superficie de la película 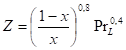 . Este esfuerzo puede ser muchas veces mayor que el esfuerzo cortante cuando no hay succión. Para determinar en qué circunstancias puede ser importante el arrastre debido al vapor sería necesario comparar
. Este esfuerzo puede ser muchas veces mayor que el esfuerzo cortante cuando no hay succión. Para determinar en qué circunstancias puede ser importante el arrastre debido al vapor sería necesario comparar 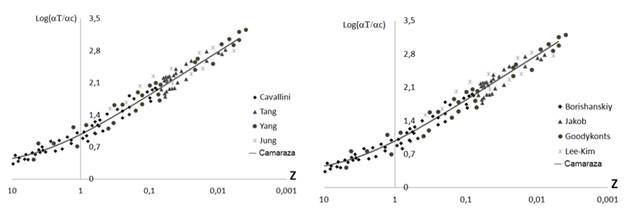 con el esfuerzo cortante en la pared cuando no existe este arrastre. Entonces el balance de fuerzas sobre la película arroja simplemente que (28):
con el esfuerzo cortante en la pared cuando no existe este arrastre. Entonces el balance de fuerzas sobre la película arroja simplemente que (28):
El espesor de la película de condensado es obtenido mediante la ecuación de Nusselt, y queda dado por (29):
Sustituyendo en (28) el valor del espesor de la película obtenido con el uso de (29) y reordenando posteriormente se llega a (30):
Como se predijo, el arrastre debido al vapor se hace más notable al aumentar 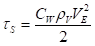 y al aumentar el cociente
y al aumentar el cociente  (ya que
(ya que 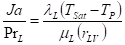 proporciona la escala de la velocidad de condensación). El arrastre se hace menos importante al aumentar la distancia
proporciona la escala de la velocidad de condensación). El arrastre se hace menos importante al aumentar la distancia  , y no hay efectos directos de la densidad del vapor
, y no hay efectos directos de la densidad del vapor 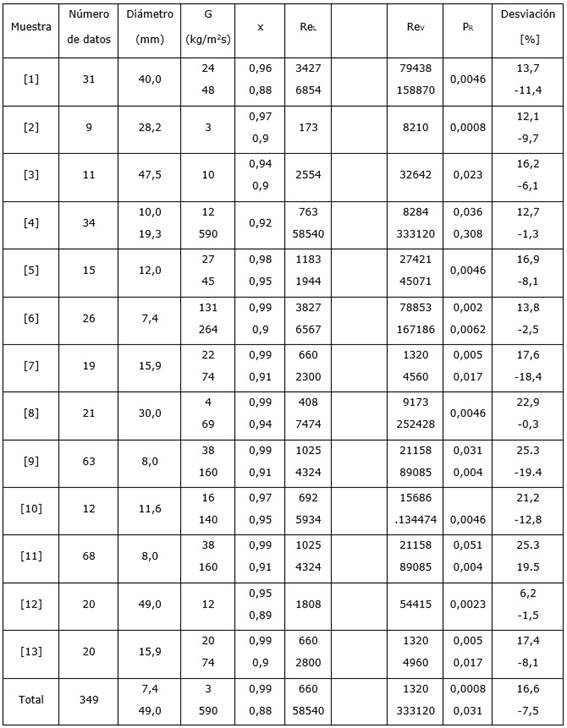 , ya que se cumple que
, ya que se cumple que 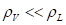
Como el perfil de velocidad es continuo, o sea  y se cumple, además, que (31):
y se cumple, además, que (31):
La expresión algebraica se torna más compleja ahora. Si se considera que  y
y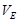 , el coeficiente local de transferencia de calor se convierte en la siguiente expresión (32):
, el coeficiente local de transferencia de calor se convierte en la siguiente expresión (32):
Por lo tanto, cuando la velocidad del vapor en un sistema ACC sea superior a los 40 m/s es necesario establecer un producto entre los resultados obtenidos mediante el empleo de la ecuación (16) y (32) para obtener el coeficiente de transferencia de calor real.
CONCLUSIONES
Se ha desarrollado un nuevo modelo que aglutina en un procedimiento unitario los tediosos procedimientos establecidos para la determinación del coeficiente medio de transferencia de calor mediante las técnicas de criterio de flujo dominante. La nueva propuesta incluye el efecto del arrastre del vapor cuando este supera la velocidad critica en el interior de ACC, y los resultados obtenidos con su empleo computan un error medio del 22 % en el 88,7 % de las muestras disponibles. Los resultados concuerdan con el criterio inicial que fundamentó la investigación, considerándose cumplidos los objetivos de la misma. El nuevo método es válido además para una calidad del vapor ubicada entre 0,9 y la unidad, para flujos de vapor entre 3 y 590 kg/(m2/s), valores para el número de Reynolds para la porción líquida entre 660 y 58 540 y del número de Reynolds para la porción vapor ubicadas entre 1 320 y 333 120, diámetros equivalentes internos de los tubos comprendidos entre los 7,4 a 49 mm.