Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.23 no.1 San José de las Lajas ene.-mar. 2014
ARTÍCULO ORIGINAL
Determinación indirecta de la capacidad de retención de humedad en suelos de la subcuenca del río Torjá, Chiquimula, Guatemala
Indirect determination of the capacity to hold moisture in soils of the sub basin of the Torjá River, Chiquimula, Guatemala
M.Sc. Rodolfo Augusto Chicas SotoI, Dr.C. Eddi Alejandro Vanegas ChacónII, Dr.C. Nancy García ÁlvarezIII
I Universidad de San Carlos (USAC), Centro Universitario de Oriente, Guatemala.
II Universidad de San Carlos (USAC), Facultad de Agronomía, Guatemala.
III Universidad de Ciego de Ávila, Centro de Estudios Hidrotécnicos, Ciego de Ávila, Cuba.
RESUMEN
La investigación tiene como objetivo determinar modelos estadísticos que permitan estimar de forma indirecta la capacidad de campo y el punto de marchitez permanente para conocer la disponibilidad de agua en el suelo con fines agrícolas en una región semiárida ubicada en la subcuenca del río Torja, en el departamento de Chiquimula, Guatemala. Fueron tomadas como base las unidades fisiográficas de la subcuenca identificándose cincuenta y siete sitios, donde se realizaron muestreos de suelos. Se definieron como variables dependientes la capacidad de campo (CC) y el punto de marchitez permanente (PMP) y como variables independientes el porcentaje de arcilla, porcentaje de limo, porcentaje de arena, densidad aparente (Da), conductividad eléctrica (CE) y la materia orgánica (MO). Fueron establecidas relaciones entre estas variables mediante regresión lineal múltiple generándose los modelos: CC = 67,31–(33,77·Da) – (0,23·porcentaje de arena), R2 0,59 y PMP = 55,05 – (28,.97·Da) – (0,23 porcentaje de arena), R2 0,69. Los modelos se validaron tomando diez muestras al azar en el área obteniendo una alta correlación de Pearson entre valores observados y valores estimados a partir de la densidad aparente y porcentaje de arena, siendo de 0,84 para el modelo de capacidad de campo y 0,85 para el de punto de marchitez permanente.
Palabras clave: capacidad de campo, punto de marchitez permanente, agua en el suelo.
ABSTRACT
This research is aimed at determining statistical models to estimate indirectly the field capacity and wilting point, to know the availability of water in the soil for agricultural purposes in a semiarid region located in the department of Chiquimula, Guatemala. Based on the physiographic units of the sub basin Torja fifty-seven sites were identified and their soils were sampled. Field capacity (FC) and permanent wilting point (PMP) were defined as dependent variables and the clay percentage, silt percentage; sand percentage, bulk density, electrical conductivity (EC), and the organic matter (OM) were defined as independent variables. Relationships were established by generating the following multiple linear regression models: FC = 67,31–(33,77Da) – (0,23 sand percentage), R2 0,59 y PMP = 55,05 – (28,97Da) – (0,23 sand percentage), R2 0,69. The models were validated taking ten random samples in the study area, obtaining a high Pearson correlation between observed and estimated values using models from the bulk density and sand percentage, being 0,84 for the model field capacity and 0,85 for the wilting point.
Key words: field capacity, wilting point, soil water.
INTRODUCCIÓN
Mantener niveles adecuados de agua en el suelo es fundamental para garantizar el éxito de las cosechas en el campo, unido a factores de manejo de los suelos, semillas mejoradas y fertilizantes. Sandoval (2007) manifiesta que existen ciertas etapas muy sensibles del ciclo del cultivo en los cuales un déficit de agua puede provocar una disminución significativa en el rendimiento pudiéndose determinar mediante experimentos que el período crítico es el de floración y formación de fruto. Según Taboada y Micucci (2002) una forma práctica de expresar y visualizar la cantidad de agua existente o almacenada en el suelo es en términos de lámina de agua. La unidad de medida más frecuente para expresar la lámina es en milímetros, que equivale al volumen de 1 litro de agua distribuido en una superficie de 1 m2. Relacionado con la temática de la estimación de las constantes de humedad, Domingo et al (2006) manifiestan que la capacidad de retención de agua en el suelo es un parámetro de base física utilizado por técnicos forestales e investigadores en ecología forestal del territorio español, como uno de los factores estimadores de las disponibilidades de agua para las plantas, la bondad de estos parámetros se contrasta mediante el análisis de correlaciones, con resultados satisfactorios. Así mismo, Martínez y Ceballos (2001) expresan que existen tres variables de predicción para estimar la humedad, tales como: las fracciones texturales, la densidad aparente y ocasionalmente la materia orgánica; estos autores afirman que los porcentajes de varianza explicada por las ecuaciones de regresión son siempre altos y que la bondad de las estimaciones, en términos de error medio y de raíz del error cuadrático medio, ha sido muy satisfactoria. La sub cuenca del río Torjá es parte del llamado corredor seco de Guatemala, por lo que el conocimiento práctico de parámetros como la capacidad de campo y el punto de marchitez permanente son claves para realizar programas de producción agrícola. Se recurre a la estimación indirecta, porque los cálculos directos son realizados en laboratorios de suelos distantes y regularmente tienen alto costo. Esta investigación trae soluciones sencillas de gran utilidad a los campesinos locales mediante la determinación de modelos estadísticos que permiten calcular estos parámetros de humedad a través de la obtención de datos de campo representativos.
MÉTODOS
Localidad
Esta investigación se realizó en la sub cuenca del río Torjá, la cual pertenece a la cuenca del Rio Grande, de la vertiente del Atlántico, con una superficie de 135,8 kilómetros cuadrados en la jurisdicción de los municipios de Jocotán, Camotán, San Juan Ermita, Olopa y Quezaltepeque, en el departamento de Chiquimula, Guatemala (AECI-SEGEPLAN, 2003). Es parte del corredor seco de Guatemala, susceptible a la sequía y alto riesgo para la agricultura de subsistencia. Su importancia radica en que comprende el 80% de la región Chortí existente en el departamento de Chiquimula, con pobladores pobres y extremadamente pobres, suelos diversos, principalmente de origen volcánico, clima cálido seco, y precipitaciones fluctuantes entre 600 y 1050 mm anuales distribuidos en los meses de mayo a octubre, donde predominan cultivos como el maíz, frijol y sorgo, así como hortalizas (Fernández y Álvaro, 2007).
Análisis de laboratorio
Durante el período experimental se definió el área de estudio y se determinaron las unidades fisiográficas presentes en la sub cuenca, lo que permitió definir unidades de mapeo e igual número de muestras. Se tomaron 57 muestras de suelos a las que se realizó los siguientes análisis: la Capacidad de Campo y el Punto de Marchitez Permanente, que fueron consideradas como variables dependientes, se determinaron mediante la metodología de la olla de presión, Richards, (1972); la textura mediante el uso de hidrómetro; la densidad aparente del suelo por la metodología de la probeta según Cervantes y Mojica, (1981); la materia orgánica por el método de Walkey y Black (1938); y la Conductividad Eléctrica formulando una solución de suelo y agua en una relación 1:2.5, para lo cual se utilizó un conductímetro digital (Calderón y Pavlova, 1999), todas estas mediciones fueron consideradas como variables independientes.
Análisis estadístico
Primeramente se analizaron los datos obtenidos de los análisis de suelos, discriminando los datos extremos. Para el tratamiento de datos se utilizo el programa de cómputo INFOSTAT propuesto por Di Rienzo et al (2001), para la regresión lineal múltiple. Se identificaron las variables independientes que de mejor forma explican asociaciones respecto a la capacidad de campo y al punto de marchitez permanente, determinándose modelos estadísticos. Se determina un primer modelo estadístico que incluye todas las variables identificando aquellas que expliquen de manera significativa los cambios en las variables dependientes y se compara con el análisis previo de correlación. Posteriormente se establece un segundo modelo que incluye sólo las variables con alta significación, determinando su porcentaje de explicación, sobre la variabilidad de las variables dependientes, a través del estadístico Eta Cuadrado. Así mismo se verifica el fundamento estadístico de los modelos mediante la determinación de intervalos de confianza al 5%, análisis de residuos y la Prueba de Shapiro & Wilks para verificar la normalidad de los residuales. Una vez determinados los modelos, éstos son validados mediante correlaciones de Pearson entre los resultados de Capacidad de Campo y Punto de Marchitez, procedentes del análisis de diez muestras aleatorias en el área de estudio, y los valores estimados a través de los modelos generados.
RESULTADOS
Los resultados del análisis de laboratorio de las muestras de suelos del área de estudio se relacionan a continuación, mostrándose en la Tabla 1.
Mediante el análisis de los resultados del laboratorio de las muestras de suelos, se realizaron varios escenarios de modelaje determinando la eliminación de seis puntos de muestreo (21, 24, 36, 39, 44 y 51), por ser extremos. Posteriormente con cincuenta y un set de datos se procedió a la realización de un análisis de correlación, para determinar que variables independientes están asociadas a la capacidad de campo y al punto de marchitez permanente. Se determinó que las variables de mayor asociación en ambos casos son la densidad aparente (Da) y el % de Arena que se muestran a continuación (Figura 1).
Posteriormente se realizó un primer modelo con todas las variables independientes (porcentaje de arcilla, (porcentaje de limo, (porcentaje de arena, densidad aparente, conductividad eléctrica y materia orgánica). Se determinó que las únicas variables que explican la variación de la CC y PMP con significación del 5% son la densidad aparente y el (porcentaje de arena, lo que coincide con el análisis previo de correlación. Esto se explica debido a que el área de estudio es una zona semiárida (de poca precipitación y alta evapotranspiración), con periodo seco prolongado, donde predominan suelos con granulometría de media a gruesa con una cobertura vegetal no frondosa y una dinámica de reciclaje de materia orgánica muy baja. Los modelos determinados se relacionan seguidamente:
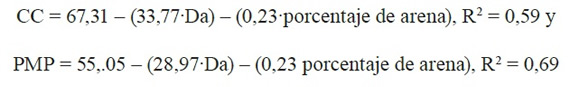
donde:
CC= Capacidad de campo. Da= Densidad aparente, PMP= Punto de marchitez permanente, R2= Coeficiente de determinación ajustado.
De conformidad con el análisis del estadístico Eta Cuadrado, para el caso de CC, la Da explica 41,32% y el porcentaje de arena 17,69% de la variabilidad, mientras que para la PMP, la Da explica el 42,86% y el porcentaje de arena 26,27% de la variabilidad.
Los modelos expresan un 59,01% para CC y un 69,13% para PMP de la variabilidad total.
La Figura 2 muestra los fundamentos estadísticos del modelo de CC; Tendencias adecuadas de los intervalos de confianza y residuos estandarizados, tendencia lineal de la prueba de Shapiro & Wilks que verifica la normalidad de los residuos.
Los modelos se validaron mediante la correlación del resultado de CC y PMP de diez muestras aleatorias de suelos en el área de estudio y los valores estimados de CC y PMP a través de los modelos. La Tabla 2 muestra los resultados de la validación.
Se observa alta correlación de Pearson entre los valores observados a nivel de campo de CC y PMP, y los estimados mediante los modelos tomando como insumos la densidad aparente y el porcentaje de arena, obteniéndose un valor de = 0.,84 para el modelo de CC y de =0,85 para el de PMP tal como aparece en Figura 3.
Se considera, por tanto, que los modelos generados para determinar las constantes de humedad pueden utilizarse adecuadamente para estudios a nivel local, ya que presentan alta probabilidad de exactitud. Es importante señalar que, utilizados adecuadamente, constituyen herramientas de apoyo a la gestión del manejo del agua en la región.
Los estudios relativos a la estimación indirecta de la capacidad de campo y el punto de marchitez, son escasos, existiendo algunas investigaciones relativas al tema de la humedad como la realizada por Castellaro y Squella (2006), quienes elaboraron un modelo simple de crecimiento, fenología y balance hídrico de praderas anuales en clima mediterráneo. Damiano y Taboada (2000) expresan que la producción de cultivos agrícolas depende, además de los aportes externos de agua, de la capacidad de agua disponible de los suelos (CAD) y su cálculo surge usualmente de conocer previamente la retención de humedad entre dos valores discretos de potencial mátrico (i.e. -33 kPa y - 1500 kPa) y la determinación de estos valores, tanto en campo como en laboratorio, es costosa en tiempo y recursos, además de demandar un gran número de muestras debido a la variabilidad espacial del suelo.
La determinación de la capacidad de retención de agua de los suelos de la cuenca del Rio Torja, mediante la utilización de los modelos determinados, es congruente con el análisis de la clase textural (Tabla 3).
Puede aseverarse entonces que la capacidad de retención de humedad muestra una estrecha relación con la textura de los suelos, puesto que los valores más altos nos indican la presencia de suelos arcillosos, mientras que la disminución del valor de la capacidad de retención nos indica la tendencia hacia suelos con granulometría media o gruesa (Sandoval, 2007).
CONCLUSIONES
• Las variables densidad aparente (Da) y % de arena, explican mayormente la variabilidad respecto a la capacidad de campo y punto de marchitez permanente.
• Ambos modelos, tienen una probabilidad mayor del 80% de estimar adecuadamente las constantes de humedad del suelo.
• La diferencia entre la capacidad de campo y el punto de marchitez permanente, determina la capacidad de retención de humedad en los suelos, parámetro con múltiples fines para la planificación agrícola.
REFERENCIAS BIBLIOGRÁFICAS
1. AECI-SEGEPLAN: Estrategia de reducción de la pobreza municipio de Jocotán, Agencia Española de Cooperación Internacional, Secretaria de Planificación y Programación, Chiquimula, España, 2003.
2. CALDERÓN, F.; M. PAVLOVA: Metodologías para análisis químico de suelos. [en línea] 1999., Disponible en: http://www.drcalderonlabs.com [Consulta: mayo 18 2003].
3. CASTELLARO, G; F. SQUELLA: Modelo simple de simulación para la estimación del crecimiento, fenología y balance hídrico de praderas anuales de clima mediterráneo. [en línea] Chile. Disponible en: http://www.castella@puc.cl [Consulta: enero 25 2006].
4. CERVANTES, C; F. MOJICA: Manual de Laboratorio de Edafología, EUNA, San José, Costa Rica, 1981.
5. DAMIANO, F; M. TABOADA: "Capacidad de agua disponible en suelos agrícolas de la pampa ondulada usando funciones de pedo-transferencia". En: Actas XVII Congreso Argentino de la Ciencia del Suelo, Comisión I- Nº 29, Mar del Plata, Argentina, 2000.
6. DI RIENZO, J.; F. CASANOVES; M. BALZARINI; L. GONZÁLEZ; M. TABLADA; W. ROBLEDO: InfoStat [en línea] versión 2011. Grupo InfoStat, FCA, Universidad Nacional de Córdoba, Argentina. , Disponible en: http://www.infostat.com.ar [Consulta: agosto 20 2012]
7. DOMINGO, J.; E. FERNÁNDEZ: Estimación de la capacidad de retención de agua en el suelo, Ed. Departamento de Ciencias Agroforestales. Universidad de Huelva, España, 2006.
8. FERNÁNDEZ, L.; G. ÁLVARO: Evaluación de cinco tratamientos de blanqueado de la hoja de palma (Sabal guatemalensis Beccari) en el municipio de Jocotán, Chiquimula. [en línea]. Tesis. Guatemala: USAC. Disponible en: http://biblioteca.usac.edu.gt/tesis/01/01_2364.pdf [Consulta: mayo 18 2007].
9. MARTÍNEZ, J.; A. CEBALLOS: Estimación de Propiedades Hídricas de los Suelos Mediante el uso de Funciones de Edafo-Transferencia. Universidad de Navarra, España, 2001.
10. RICHARDS, L.: Suelos Salinos y Sódicos. Editorial Limusa S.A., México, 1972.
11. SANDOVAL, J.: Principios de Riego y Drenaje. Editorial Universitaria, Universidad de San Carlos de Guatemala, Guatemala, 2007.
12. TABOADA, M.; F. MICUCCI: Fertilidad física de los suelos, Editorial Facultad Agronomía, Universidad de Buenos Aires, Argentina, 2002.
13. WALKLEY, A. & I. BLACK: An examination of the Degtjareff method and a proposed modification of the chromic matter and a proposed modification of the chromic acid titration method, Soil Sci., (37): 29-38, 1934.
Recibido: 19 de julio de 2012.
Aprobado: 5 de septiembre de 2013.
Rodolfo Augusto Chicas Soto. Universidad de San Carlos (USAC), Centro Universitario de Oriente, Guatemala. Correo electrónico: ingchicas@yahoo.com














