Artículo original

Predicción de la afinidad de ligandos antagonistas por receptores de adenosina A_2A usando árboles de decisión

Predicting the affinity of A_2A adenosine receptor antagonists using decision trees

Adonis Huici Corrales¹  , Aliuska Morales Helguera^{1  *}  , Evys Ancede Gallardo^{1  2}  , Reinaldo Molina Ruiz¹  , Marta Teijeira Bautista³  , Guillermo Abreu Stincer⁴  , Eugenio Martínez Albelo⁴ 

¹Centro de Bioactivos Químicos, Universidad Central Marta Abreu de Las Villas. Santa Clara. Villa Clara. Cuba. CP 54830

²Centro de Nanociencias Aplicadas (CENAP), Universidad Andrés Bello. Ave República 275. Santiago. Santiago. Chile.

³Departamento de Química Orgánica, Facultad de Farmacia, Universidad de Santiago de Compostela.. Santiago de Compostela. La Coruña. España. 15782

⁴Departamento de Química, Universidad Central Marta Abreu de Las Villas. Santa Clara. Villa Clara. Cuba. CP 54830.

RESUMEN

Las enfermedades neurodegenerativas están siendo tratadas mediante la modulación de los receptores de adenosina con antagonistas más eficaces, seguros y selectivos. El objetivo del estudio consistió en desarrollar una metodología para obtener modelos de clasificación sobre la base de algoritmos de árboles de decisión y descriptores de 0D a 2D de familias no congenéricas de compuestos orgánicos para predecir cualitativamente la afinidad ligando-RAA_2A. Para ello se construyó y curó una base de datos no congenérica de 315 antagonistas con su constante de inhibición en nano molar, etiquetados como potentes y débiles. Se utilizaron los programas Dragon e ISIDA/QSPR para calcular descriptores moleculares y se obtuvieron cinco grupos de descriptores. En cada grupo se seleccionaron 50 descriptores usando el criterio mRMR. La base de datos se dividió en series de Entrenamiento, Prueba y Externa mediante una selección aleatoria y un análisis de clúster k-means generalizado. Se desarrollaron y validaron clasificadores utilizando el programa WEKA. Los resultados fueron analizados mediante las pruebas estadísticas de Friedman y Wilcoxon. Se comprobó la influencia significativa del parámetro m del algoritmo J48 en la predictividad, para los modelos que usaron los descriptores de los grupos aug.a-b e hyb.aug.a del ISIDA/QSPR. El modelo de mejor desempeño se obtuvo de los descriptores seleccionados del grupo ISIDA-todos con un valor de m=6 y alcanzó 90.6% de predicción sobre la serie Externa. La metodología desarrollada para obtener modelos de clasificación sobre la base de algoritmos de árboles de decisión y descriptores de 0D a 2D de familias no congenéricas de compuestos orgánicos es efectiva para predecir cualitativamente la afinidad ligando-RAA_2Acon una exactitud, especificidad y selectividad superiores al 90%.

Palabras-clave: aprendizaje automatizado; clasificación; modelación; QSAR

ABSTRACT

Neurodegenerative diseases are being treated by modulating adenosine receptors with more effective, safe and selective antagonists. The objective of the study was to develop a methodology to obtain classification models based on decision tree algorithms and descriptors from 0D to 2D of non-congenital families of organic compounds to qualitatively predict ligand-RAA_2A affinity. For this purpose, a non-congeneric database of 315 antagonists was constructed and cured with its inhibition constant in nano molar, labeled as potent and weak. The Dragon and ISIDA / QSPR programs were used to calculate molecular descriptors and five groups of descriptors were obtained. In each group 50 descriptors were selected using the mRMR criterion. The database was divided into Training, Test and External series through a random selection and a generalized k-means cluster analysis. Classifiers were developed and validated using the WEKA program. The results were analyzed using the statistical tests of Friedman and Wilcoxon. The significant influence of parameter m of algorithm J48 on the predictivity was verified for the models that used the descriptors of the aug.a-b and hyb.aug.a groups of ISIDA / QSPR. The best performance model was obtained from the selected descriptors of the ISIDA-all group with a value of m = 6 and reached 90.6% prediction on the External series. The methodology developed to obtain classification models based on decision tree algorithms and descriptors from 0D to 2D of non-congenital families of organic compounds is effective in qualitatively predicting ligand-RAA_2A affinity with accuracy, specificity and selectivity greater than 90 %.

Key words: classification; machine learning; modeling; QSAR

INTRODUCCIÓN

El avance de las tecnologías informáticas y la disponibilidad creciente de fuentes de información han propiciado el surgimiento y desarrollo de nuevos campos de estudio. Tal es el caso de la Quimioinformática y la Bioinformática cuyo objetivo es modelar in silico fenómenos reales de la naturaleza. Dentro de estas ramas los análisis cuantitativos de estructura-actividad (QSAR, por sus siglas del inglés: Quantitative Structure-Activity Relationship) gozan de gran aceptación en la comunidad científica por su relativa sencillez e interpretación. Mediante su aplicación se pueden desarrollar modelos matemáticos para predecir la actividad biológica o la potencia de nuevos compuestos. QSAR se basan en el precepto de que moléculas con estructuras semejantes deben presentar propiedades semejantes. Mediante algoritmos lógico matemáticos se calculan descriptores moleculares, que son variables que codifican la información estructural de las moléculas. Luego utilizando técnicas de aprendizaje automatizado y minería de datos, se pueden obtener y validar modelos de regresión y clasificación que permiten, dentro de ciertos límites, predecir la propiedad que se desea modelar (^{Taylor y Triggle, 2007}; ^{Roy et al., 2015}).

Los estudios QSAR se han aplicado en varias áreas del conocimiento para resolver problemas tanto académicos y regulatorios, como industriales. Entre estos se pueden mencionar la identificación y optimización de sustancias con uso farmacológico, biocidas o plaguicidas, evaluación de la toxicidad de sustancias tanto para el hombre como para otras especies, predicción del destino de sustancias liberadas al medio ambiente, racionalización y predicción del efecto combinado de sustancias en mezclas y formulaciones y la selección de compuestos con óptimas propiedades farmacocinéticas como la bioestabilidad y la biodisponibilidad, entre otras (^{Cronin, 2010}; ^{Roy et al., 2015}).

Un campo donde se utilizan ampliamente estas técnicas es en el diseño racional de fármacos. Esta forma de diseño, demuestra teóricamente la potencialidad que tiene una sustancia para ser utilizada como ingrediente farmacológico activo, antes de ser probada en modelos biológicos reales o incluso antes de ser obtenida. De esta forma se pretende disminuir recursos y el tiempo que demora en salir al mercado un nuevo fármaco (^{Braga et al., 2014}; ^{Gomes et al., 2017}).

La adenosina es un nucleósido endógeno que regula varias funciones vitales en el organismo como la frecuencia cardíaca, la memoria, los procesos inflamatorios y el balance energético a través de la interacción de varias sustancias con sus receptores (RA): A₁, A_2A, A_2B, A₃ (^{Gao y Jacobson, 2007}). La activación o desactivación de estos RA ha sido ampliamente estudiada y se ha de mostrado que juegan un papel fundamental en la génesis y evolución de varias enfermedades (^{Wilson y Mustafa, 2009}). Específicamente los receptores A_2A (RAA_2A) están vinculados a trastornos neurodegenerativos como Parkinson (^{Kase, 2000}) y Alzheimer (^{Rahman, 2009}). El uso de sustancias antagonistas a este receptor pueden prevenir la aparición o desarrollo de dichas enfermedades. En el mercado mundial se comercializan fármacos con acción sobre estos receptores para el tratamiento de algunas de estas enfermedades (^{Müller y Jacobson, 2011}) pero la investigación de antagonistas más efectivos y específicos aún sigue en estudio (^{Diniz et al., 2008}; ^{González et al., 2008}; ^{Bacilieri et al., 2013}; ^{Sousa y Diniz, 2017}).

La aplicación de técnicas para el cribado de bases de datos de posibles sustancias antagonistas de RAA_2A han resultado avances científicos presentados por varios autores (^{Drabczyńska et al., 2007}; ^{Mustyala et al., 2012}; ^{Bacilieri et al., 2013}; ^{Zhang et al., 2014}; ^{Pourbasheer et al., 2015}; ^{Khanfar et al., 2016}; ^{Kalash et al., 2017}; ^{Fan et al., 2019}). La metodología general consiste en optimizar estructuras 3D de las sustancias a ensayar con docking molecular y luego mediante técnicas de aprendizaje automatizado crear un modelo de regresión lineal con descriptores moleculares 3D, que permite predecir la actividad de sustancias dentro de un determinado dominio de aplicación. Sin embargo, el costo computacional de estas técnicas es alto y requieren algoritmos de difícil interpretación.

Técnicas más sencillas han sido poco estudiadas, tal es el caso de la clasificación usando descriptores de conteo de fragmentos y de propiedades físicas para construir modelos de QSAR a través de algoritmos no lineales como los árboles de decisión (^{Quinlan, 1986}), que permiten una mejor interpretación. Por otra parte, la modelación de propiedades está limitada a un dominio de aplicación determinado por las estructuras utilizadas para su desarrollo. De manera general los modelos que utilizan series de estructuras comunes (series congenéricas), tienden a ser más precisos, pero tienen menor dominio de aplicación comparados con aquellos que se desarrollan a partir de series no congenéricas (^{Pérez, 2010}, ^{Morales et al., 2013}). Atendiendo a lo anterior, el objetivo del estudio consistió en desarrollar una metodología para obtener y evaluar modelos de clasificación sobre la base de algoritmos de árboles de decisión y descriptores de 0D a 2D de familias no congenéricas de compuestos orgánicos para predecir cualitativamente la afinidad ligando-RAA_2A.

MATERIALES Y MÉTODOS

Base de datos

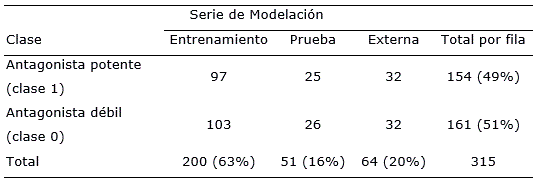
La base de datos de antagonistas sobre RAA_2A fue recopilada de la literatura científica (^{Cristalli et al., 1998}; ^{Klotz et al., 2003}; ^{Novellino et al., 2005}; ^{Lenzi et al., 2006}; ^{Moro et al., 2006}; ^{Colotta et al., 2007}; ^{Colotta et al., 2008}; ^{Colotta et al., 2009}; ^{Da Settimo et al., 2007}; ^{Michielan et al., 2008}; ^{Cosimelli et al., 2008}; ^{Michielan et al., 2009a}; ^{Michielan et al., 2009b}; ^{Lambertucci et al., 2009}; ^{Cheong et al., 2010}; ^{Taliani et al., 2010}; ^{Taliani et al., 2013}; ^{Gaspar et al., 2012}). Esta contiene 327 sustancias químicas con sus valores de constantes de inhibición (Ki) de RAA_2A. Los datos fueron tomados de varios estudios, pero el protocolo de ensayo fue el mismo (^{Klotz et al., 1997}). Todos los antagonistas fueron evaluados empleando técnicas de marcado radioactivo usando el (3H)NECA como radioligando y una matriz biológica de RAA_2A, expresados en células CHO (Chinese hamster ovary). Después de un proceso de curación de la base de datos, fueron retenidos 315 compuestos para este estudio, Tabla S1 en materiales suplementarios). Sus estructuras químicas fueron codificadas en formato sdf y sus constantes de inhibición (Ki) fueron expresadas en nM. En el conjunto de datos, el rango de la Ki varió desde 4 nM hasta > 10 000 nM. De acuerdo con estos valores los compuestos fueron distribuidos en dos clases: 1) antagonistas potentes, con valores de Ki ≤ 1000 nM y 2) antagonistas débiles, con valores de Ki > 1 000 nM. Como resultado de esta partición, 154 compuestos fueron considerados como antagonistas potentes y 161 como débiles (Tabla 1).

Tabla 1 Distribución de los casos por clases (antagonistas potentes/antagonistas débiles) y por series (entrenamiento y prueba) para su utilización en el proceso de modelación QSAR. 

Curación de la Base de datos

La base de datos fue curada siguiendo el protocolo propuesto por ^{Fourches et al. (2010)}. Este procedimiento incluyó remoción de mezclas y sales, normalización de quimiotipos, como grupos nitro, inclusión de hidrógeno explícito, análisis y remoción de duplicados. Para la normalización estructural y eliminación de sales se utilizó el programa Standardizer de ChemAxon (^{ChemAxon, 2015}), mientras que los duplicados fueron identificados, analizados y removidos usando la herramienta EdiSDF del programa ISIDA/QSPR (^{Varnek y Solov’ev, 2010}). Finalmente se realizó un chequeo manual de cada estructura para verificar que las estructuras eran correctas.

Descriptores: un total de 3 407 descriptores moleculares fueron usados en el estudio. Estos fueron calculados con los programas Dragon (^{Talete, 2010}) e ISIDA/QSPR (^{Varnek y Solov’ev, 2010}).

Descriptores Dragon: incluyeron descriptores constitucionales, grupos funcionales y fragmentos centrados en átomos. Los descriptores constitucionales son los más simples y solo reflejan la composición de una molécula sin ninguna información geométrica. Ejemplo de estos descriptores son: números de átomos, enlaces, anillos, tipos de átomos específicos, enlaces rotables, etc. Por su parte los grupos funcionales y fragmentos centrados en átomos son descriptores de conteo con valores enteros (^{Todeschini y Consonni, 2009}).

Descriptores ISIDA: estos son descriptores de conteo de fragmentos 2D, los cuales se basan en la división de un grafo molecular en subgrafos. Tres tipos de fragmentos fueron usados: secuencias (a-b), átomos aumentados (aug.a-b) y átomos aumentados hibridizados (hyb.aug.a). El primer tipo representa secuencias lineales de átomos (A, atoms) y enlaces (B, bonds). Solo los caminos más cortos de un átomo a otro fueron usados y solo las secuencias entre dos y ocho átomos de longitud fueron calculadas. El segundo tipo de fragmento (átomos aumentados) representa un átomo y su ambiente inmediato, incluyendo átomos y enlaces. La hibridación atómica (hyb.aug.a) fue también considerada para los átomos aumentados con lo que se obtuvo un tercer tipo de fragmento, los átomos aumentados hibridizados.

Con los descriptores calculados se construyeron cinco bases de datos diferentes y fueron nombradas según la información estructural que contenían: 1) a-b (ISIDA-secuencias), 2) aug.a-b (ISIDA-átomos aumentados), 3) hyb.aug.a (ISIDA- átomos aumentados hibridados), 4) ISIDA-todos (contiene todos los descriptores anteriores), 5) Dragon 0D-1D. Estas bases de datos contienen los mismos compuestos de la serie de entrenamiento y solo varían los descriptores asociados a los casos.

Estudios anteriores (^{Hawkins, 2004}), demostraron que una reducción de descriptores redundantes y poco significativos mejora la calidad de los modelos. Teniendo en cuenta este criterio, se adoptó la siguiente estrategia. Los descriptores con poca varianza y altamente correlacionados (r > 0.95) se removieron, y se obtuvieron: 151 descriptores Dragon y 3256 descriptores ISIDA. Adicionalmente, se utilizó el algoritmo Mínima Redundancia Máxima Relevancia (mRMR), implementado en el programa mrmr_win32 (^{Hanchuan et al., 2005}), para seleccionar los 50 descriptores más relevantes para la variable respuesta y menos redundantes entre sí, en cada una base de datos.

Selección de las series de entrenamiento, prueba y externa

La serie externa se extrajo por muestreo aleatorio de la base de datos curada (alrededor del 20%) usando para ello el programa STATISTICA. El resto de los compuestos se usaron en la serie de modelación, la cual se dividió en serie de entrenamiento y serie de prueba, mediante un análisis de clúster (k-means) generalizado en el programa STATISTICA. Este análisis tiene como ventaja principal que al usar un algoritmo de validación cruzada v-veces es posible determinar automáticamente el número de clúster. El método fue aplicado por separado a cada clase de la serie de modelación (clase 1: 122 compuestos y clase 0: 129 compuestos) y consideró los parámetros que se describen a continuación. Valor de v: 10, semilla: 1402939, número mínimo de clúster: 2, número máximo de clúster: 25, menor porcentaje de decrecimiento: 5, función de distancia: distancia euclidiana. Los descriptores que se utilizaron fueron 59 componentes principales derivados de los descriptores 0D-2D calculados con el programa Dragon. Estos componentes principales son correlaciones lineales de los descriptores Dragon originales que condensan la información de estos y brinda mayor información estructural que los de fragmentos del ISIDA al tener en cuenta información referente a la matriz de distancia y a índices topológicos de la molécula.

Después de creados los clústeres, los casos fueron ordenados por distancia euclidiana a su respectivo centroide y se extrajo de cada uno el 20% de los compuestos para conformar la serie de prueba. Con esto se garantiza que las estructuras de la serie prueba sean representativas del conjunto de modelado y propicia que estén dentro del dominio de aplicación del modelo generado usando la serie de entrenamiento. El 80% restante de los casos conformó la serie de entrenamiento de los modelos de clasificación.

Modelación QSAR

La modelación QSAR incluyó tres pasos: i) curación, preparación y análisis de los datos (selección de compuestos y descriptores), ii) construcción de modelos y iii) validación y selección del mejor modelo. Los modelos o clasificadores fueron construidos y validados usando la serie de modelación, mientras que la serie externa fue reservada solo para evaluar el poder predictivo real del modelo seleccionado.

Para cumplir el objetivo trazado se construyeron y evaluaron clasificadores basados en el algoritmo de árboles de decisión J48. Los clasificadores fueron generados variando 1) el conjunto de descriptores y generando diferentes bases y 2) variando el parámetro m en el algoritmo J48. Como algoritmo de aprendizaje para la generación de los clasificadores se usó el árbol de decisión J48, una implementación del algoritmo C4.5 (^{Quinlan, 1993}), disponible en el programa WEKA (^{Witten et al., 2011}). Este algoritmo construye árboles de decisión usando una serie de entrenamiento y se basa en el criterio de ganancia de información normalizada para medir cuán bien un descriptor separa los casos del entrenamiento (^{Witten et al., 2011}).

En la construcción de un árbol J48, el número de casos mínimo en nodos terminales (m) es un parámetro importante que elimina descriptores que ocasionan ruido y sobreajuste (^{Witten et al., 2011}). En este trabajo se estudió la influencia de ese parámetro en el desempeño de los clasificadores obtenidos. Para ello, se varió m desde 2 hasta 20. El resto de los parámetros establecidos para este clasificador tomaron los valores por defecto del programa WEKA.

Según las normas de ^{OECD (2004)}, un modelo QSAR debe tener bondad de ajuste, robustez y capacidad de generalización. La bondad de ajuste fue evaluada teniendo en cuenta el desempeño de los modelos al predecir el conjunto de entrenamiento, mientras que la robustez fue medida empleando una técnica de validación cruzada 5-veces y 10-veces. El conjunto de prueba fue usado para la validación interna y para la selección del mejor modelo comprobando su capacidad generalizadora. Finalmente, el desempeño real de los clasificadores fue evaluado con una predicción sobre la serie externa que no fue usada en la construcción, validación y selección de los modelos. Las medidas utilizadas para estas evaluaciones fueron: área bajo la curva (AUC, area under the curve), estadígrafo Kappa, exactitud, selectividad y especificidad. Estos parámetros oscilan entre 0 y 1, valores más cercanos a 1 corresponden a clasificadores con mejor desempeño

Análisis estadístico de los clasificadores

Con el objetivo de evaluar que descriptores ofrecían modelos con mejor desempeño, así como determinar la influencia del parámetro m sobre la calidad de los árboles de decisión se utilizaron las pruebas no paramétricas de Friedman y Wilcoxon para pares coincidentes (^{Sheskin, 2000}). Estas se realizaron mediante el programa SPSS y se consideró un nivel de significación de 0.05 en cada una.

RESULTADOS Y DISCUSIÓN

Como resultado del estudio se obtuvieron 50 árboles de decisión (valores de sus estadígrafos en la Tabla S1 en materiales suplementarios). En la (figura 1, se presenta el comportamiento de la exactitud media de los clasificadores por base y para cada valor del parámetro m. Este valor de exactitud media es el resultado de promediar la exactitud de los conjuntos de entrenamiento, validación (v=5 y v=10) y prueba.

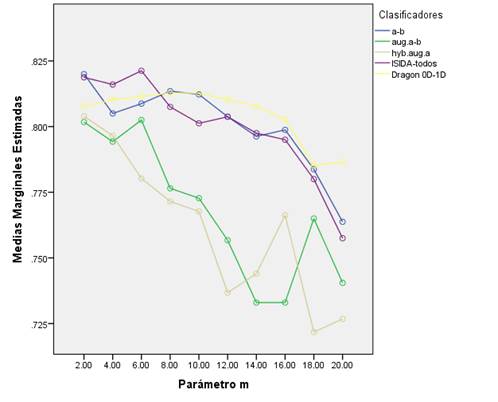
Figura 1 Exactitud media calculada para los clasificadores generados de cada base de datos al variar el parámetro m en el algoritmo J48. 

De manera general se apreció que los árboles de decisión con mejor desempeño fueron los que utilizaron los descriptores de secuencia de átomos (a-b), la combinación de todos los descriptores del ISIDA (ISIDA-todos) y la combinación de todos los descriptores 0D-1D del Dragon. En contraste, los peores resultados se observaron en los modelos que usaron los descriptores de átomos aumentados (aug.a-b) y átomos hibridizados aumentados (hyb.aug.a) implementados ambos en el programa ISIDA. Los árboles de decisión son grafos acíclicos donde cada nodo especifica una prueba de algún rasgo, y cada arco que sale del nodo corresponde a alguno de los valores posibles del rasgo que representa ese nodo. Al enfrentarse a un caso desconocido, se le aplica la prueba correspondiente del nodo raíz y en dependencia del resultado logrado se evalúa el nodo siguiente. Este proceso continúa hasta alcanzar un nodo hoja o terminal que define la clasificación (^{Mitchell, 1997}). Los algoritmos base para construir árboles de decisión se conocen como ID3 (^{Quinlan, 1986}), pero estos presentan limitaciones como el alto riesgo de sobreentrenamiento y el hecho de que trabajan con atributos de dominio discreto. El sobreentrenamiento de un modelo es un fenómeno que ocurre cuando se entrena con una serie de datos pequeña; el clasificador obtenido tiene una alta capacidad predictiva sobre ellos, pero al introducir nuevos casos tiende a confundir la asignación de sus clases. El algoritmo C4.5 (^{Quinlan, 1993}), es una variante de los ID3 que se usa para solucionar estas limitantes. Se basa en la utilización del criterio razón de ganancia (gain ratio), con lo que consigue evitar que las variables con mayor número de posibles valores salgan beneficiadas en la selección. Para evitar el sobreentrenamiento, utiliza puntos de corte e introduce varias medidas, en particular los criterios de parada de la división y de poda del árbol (^{Franco, 2011}).

Por otra parte, se observó que el aumento del parámetro m logró, como tendencia general, un decrecimiento de los valores medios de la exactitud de los modelos. Este resultado es lógico si se tiene en cuenta que el aumento de este parámetro decrece la profundidad del árbol, evita el sobreajuste y la introducción de descriptores no significativos (^{Witten et al., 2011}). A pesar de esta tendencia, se apreció que los árboles que emplearon los descriptores del Dragon mantuvieron una estabilidad en sus valores de exactitud con el aumento de m. El resto de los clasificadores J48 alcanzaron sus mejores desempeños cuando m ≤ 10.

El mayor valor de exactitud media alcanzado, sugiere que el árbol de mejor desempeño fue aquel que utilizó los descriptores más relevantes y menos redundantes del conjunto de todos los descriptores del ISIDA con un valor de m = 6 (Figura 1, Tabla S1 del material suplementario). Este clasificador presentó una exactitud de 89.0%, 83.0%, 79.5% y 76.5% para la serie de entrenamiento, validación cruzada v= 5, validación cruzada v= 10 y prueba, respectivamente. Otros estadígrafos que avalan la calidad de este clasificador son Kappa y AUC, cuyos valores fueron: 0.780 y 0.958 respectivamente. Valores próximos a 1 de ambos estadígrafos indican que el clasificador está más cercano a un clasificador perfecto, donde la razón de falsos positivos sería de 0%.

El árbol de decisión J48 referido anteriormente contenía 11 nodos terminales (hojas) y un mínimo de seis casos por nodo terminal (Figura 2). Los descriptores eran del tipo secuencia de átomos y enlaces, con excepción de las variables C(H)(H)(H)(C) y H(N) que pertenece a los descriptores átomos hibridizados aumentados. El primer nodo contiene la serie de entrenamiento con un total de 200 antagonistas (97 potentes y 103 débiles). Este nodo se dividió en dos nuevos nodos por el descriptor N*N*C-C*O y si este aparece en la estructura molecular (denotado en la rama del árbol con >0) el caso es clasificado como antagonista potente (clase 1), de lo contrario su clasificación depende del descriptor N*C-N. En cuyo caso si el fragmento N*C-N no aparece (valor en la rama del árbol <=0) se clasifica como antagonista débil, y se obtiene un nodo terminal con 41 casos bien clasificados y uno mal clasificado. En caso de que el fragmento N*C-N aparezca (valor en la rama del árbol > 0) su clasificación depende del fragmento H-C*N*C*N*C-H. Si este fragmento aparece, el árbol lo clasifica como antagonista débil y se observa que en la serie de entrenamiento 18 casos cumplen esta condición y están bien clasificados por el modelo. Si el fragmento anterior no aparece (<=0), entonces la clasificación del caso depende del C-O-C*C*C*C-C=O. Este proceso de interpretación del árbol se continúa desarrollando hasta que todos los casos estén clasificados en nodos terminales.

Muchos estudios QSAR carecen de análisis estadísticos para establecer comparaciones modelos y se quedan en el marco de lo gráfico, lo visual y lo analítico. Sin embargo, el análisis estadístico realizado, específicamente la prueba de Friedman, para comparar los resultados de los clasificadores generados con las cinco bases diferentes: a-b, aug.a-b, hyb.aug.a, ISIDA-todos, Dragon 0D-1D, demostró que se encontraron diferencias significativas en los resultados de las exactitudes de los árboles generados con las diferentes bases de datos (p < 0.05). Este resultado tiene gran importancia ya que permite hacer una mejor selección de los clasificadores. Los modelos QSAR relacionan descriptores moleculares con propiedades biológicas y tienen gran utilidad en el desarrollo de nuevos medicamentos (^{Roy et al., 2015}).

Figura 2 Árbol de decisión J48 de mejor desempeño que utilizó los descriptores Isida-todos y un valor de m = 6. 

De los rangos promedios obtenidos en la prueba de Friedman y los valores del estadígrafo de Wilcoxon se pudo observar que los rangos medios de Friedman de los modelos ISIDA(a-b), ISIDA-todos y Dragon eran superiores al resto, lo que quedó confirmado con la prueba de Wilcoxon (Tabla 2). Por tanto, no existieron diferencias significativas entre las exactitudes medias de los modelos ISIDA(a-b), ISIDA-todos y Dragon y sus valores fueron superiores a las del resto de las bases de datos. Se distinguieron claramente dos grupos de clasificadores atendiendo a los descriptores que usaron en cada caso (Figura 1).

Tabla 2 Rangos promedios de la exactitud media de los clasificadores obtenidos de la prueba de Friedman y significación de la prueba de Wilcoxon en el desempeño de los modelos ISIDA(a-b)(aug.a-b),(hyb.aug.a.), ISIDA-todos y Dragon. 

La prueba de Friedman mostró que el parámetro m tuvo una influencia significativa en el desempeño de los clasificadores modelo aug.a-b y hyb.aug.a (p<0.05). Ello significó que el ajuste del parámetro m consiguió mejora significativa de la exactitud en esos clasificadores. En el resto de los árboles solo se lograron ligeras diferencias en la exactitud al variar este parámetro.

Teniendo en cuenta estos resultados estadísticos, así como su comportamiento general, se decidió elegir el modelo que utiliza los descriptores ISIDA-todos y el parámetro m = 6, como mejor modelo de clasificación. La Figura 3 muestra los valores de exactitud, especificidad, selectividad para la serie externa y confirma la elección anterior. El modelo ISIDA-todos logra mejor capacidad generalizadora de la serie externa (exactitud = 0.906, especificidad = 0.875 y selectividad = 0.938) cuando el valor de m = 6.

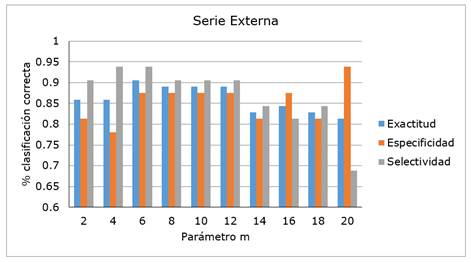
Figura 3 Valores de exactitud, especificidad y selectividad de la serie Externa de los modelos J48 para los descriptores del conjunto ISIDA-todos variando el parámetro m. 

La metodología empleada condujo a que se desarrollaron y validaron 50 modelos teóricos de clasificación. El árbol de decisión de mejor desempeño utilizó los descriptores de fragmentos del programa ISIDA\QSPR, y un número mínimo de seis casos en nodos terminales. Su validación con una serie externa demostró la mejor capacidad predictiva, específicamente valores de 90.6%, 87.5% y 93.8% para la exactitud, especificidad y selectividad, respectivamente.

La metodología consistió en:

• -​ conformar una base de datos de antagonistas de receptores de adenosina A_2A,

• -​ curación de la Base de datos,

• -​ cálculo de descriptores moleculares,

• -​ construcción de cinco bases de datos con los descriptores moleculares con una reducción de descriptores redundantes y poco significativos para mejorar la calidad de los modelos,

• -​ utilización del algoritmo Mínima Redundancia Máxima Relevancia (mRMR) para seleccionar los 50 descriptores más relevantes para la variable respuesta y menos redundantes entre sí en cada una de las base de datos,

• -​ división de la base de datos en las series de entrenamiento, prueba y externa mediante una selección aleatoria y un análisis de clúster k-means generalizado,

• -​ modelación QSAR donde se construyeron y evaluaron clasificadores basados en el algoritmo de árboles de decisión J48 y,

• -​ análisis de los resultados mediante las pruebas estadísticas de Friedman y Wilcoxon,

Este trabajo constituye un estudio exploratorio de la capacidad de modelos de clasificación basados en árboles de decisión y descriptores moleculares 0D-2D para predecir la afinidad de antagonistas por receptores de adenosina A_2A. La metodología empleada pudiera aplicarse a otros estudios similares.

CONCLUSIONES

La metodología desarrollada para obtener y evaluar modelos de clasificación sobre la base de algoritmos de árboles de decisión y descriptores de 0D a 2D de familias no congenéricas de compuestos orgánicos es efectiva para predecir cualitativamente la afinidad ligando-RAA_2A con una exactitud, especificidad y selectividad superiores al 90%.

REFERENCIAS

Bacilieri M, Ciancetta A, Paoletta S, Federico S, Cosconati S, Cacciari B, Taliani S, Da Settimo F, Novellino E, Klotz KN, Spalluto G, Moro S (2013) Revisiting a Receptor-Based Pharmacophore Hypothesis for Human A 2A Adenosine Receptor Antagonists. Journal of Chemical Information and Modeling 53(7): 1620-1637; doi:10.1021/ci300615u

Braga R, Alves V, Silva M, Muratov E, Fourches D, Tropsha A (2014) Tuning hERG Out: antitarget QSAR models for drug development. Curr Top Med Chem14: 1399-1415; doi:10.2174/1568026614666140506124442

ChemAxon (2015) ChemSuit. Disponible en: http://www.chemaxon.com. Consultado 23/04/2017

Cheong SL, Dolzhenko A, Kachler S, Paoletta S, Federico S, Cacciari B, Dolzhenko A, Klotz KN, Moro S, Spalluto G, Pastorin G (2010) The Significance of 2-Furyl Ring Substitution with a 2-( para -substituted) Aryl Group in a New Series of Pyrazolo-triazolo-pyrimidines as Potent and Highly Selective hA 3 Adenosine Receptors Antagonists: New Insights into Structure Affinity Relationship. Journal of Medicinal Chemistry 53(8): 3361-3375; doi:10.1021/jm100049f

Colotta V, Catarzi D, Varano F, Capelli F, Lenzi O, Filacchioni G, Martini C, Trincavelli L, Ciampi O, Pugliese AM, Pedata F, Schiesaro A, Morizzo E, Moro S (2007) New 2-Arylpyrazolo (3,4-c) quinoline Derivatives as Potent and Selective Human A 3 Adenosine Receptor Antagonists. Synthesis, Pharmacological Evaluation, and Ligand Receptor Modeling Studies. Journal of Medicinal Chemistry 50(17): 4061-4074; doi:10.1021/jm070123v

Colotta V, Catarzi D, Varano F, Lenzi O, Filacchioni G, Martini C, Trincavelli L, Ciampi O, Traini C, Pugliese AM, Pedata F, Morizzo E, Moro S (2008) Synthesis, ligand receptor modeling studies and pharmacological evaluation of novel 4-modified-2-aryl-1,2,4-triazolo(4,3-a)quinoxalin-1-one derivatives as potent and selective human A3 adenosine receptor antagonists. Bioorganic & Medicinal Chemistry 16(11): 6086-6102; doi:10.1016/j.bmc.2008.04.039

Colotta V, Lenzi O, Catarzi D, Varano F, Filacchioni G, Martini C, Trincavelli L, Ciampi O, Pugliese AM, Traini C, Pedata F, Morizzo E, Moro S (2009) Pyrido (2,3-e)-1,2,4-triazolo (4,3- a )pyrazin-1-one as a New Scaffold To Develop Potent and Selective Human A 3 Adenosine Receptor Antagonists. Synthesis, Pharmacological Evaluation, and Ligand Receptor Modeling Studies. Journal of Medicinal Chemistry 52(8): 2407-2419; doi:10.1021/jm8014876

Cosimelli B, Greco G, Ehlardo M, Novellino E, Da Settimo F, Taliani S, La Motta C, Bellandi M, Tuccinardi T, Martinelli A, Ciampi O, Trincavelli ML, Martini C (2008) Derivatives of 4-Amino-6-hydroxy-2-mercaptopyrimidine as Novel, Potent, and Selective A 3 Adenosine Receptor Antagonists. Journal of Medicinal Chemistry 51(6): 1764-1770; doi:10.1021/jm701159t

Cristalli G, Camaioni E, Costanzi S, Vittori S, Volpini R, Klotz KN (1998) Characterization of potent ligands at human recombinant adenosine receptors. Drug Development Research 45(3-4): 176-181; doi:10.1002/(SICI)1098-2299(199811/12)45:3/4176::AID-DDR143.0.CO;2-G

Cronin MT (2010) Quantitative Structure Activity Relationships (QSARs) Applications and Methodology. En: Puzyn T, Leszczynski J, Cronin MT (Eds). Recent Advances in QSAR Studies, pp. 3-11. Springer Netherlands, Dordrecht; doi: 10.1007/978-1-4020-9783-6_1

Da Settimo F, Primofiore G, Taliani S, Marini AM, La Motta C, Simorini F, Salerno S, Sergianni V, Tuccinardi T, Martinelli A, Cosimelli B, Greco G, Novellino E, Ciampi O, Trincavelli ML, Martini C (2007) 5-Amino-2-phenyl(1,2,3)triazolo(1,2-a)(1,2,4)benzotriazin-1-one: A versatile scaffold to obtain potent and selective A3 adenosine receptor antagonists. Journal of Medicinal Chemistry 50(23): 5676-5684; doi:10.1021/jm0708376

Diniz C, Borges F, Santana L, Uriarte E, Oliveira JMA, Gonçalves J, Fresco P (2008) Ligands and therapeutic perspectives of adenosine A(2A) receptors. Current pharmaceutical design 14(17): 1698-1722; doi:10.2174/138161208784746842

Drabczyńska A, Müller CE, Schiedel A, Schumacher B, Karolak-Wojciechowska J, Fruziński A, Zobnina W, Yuzlenko O, Kieć-Kononowicz K (2007) Phenylethyl-substituted pyrimido (2,1-f)purinediones and related compounds: Structure activity relationships as adenosine A1 and A2A receptor ligands. Bioorganic & Medicinal Chemistry 15(22): 6956-6974; doi:10.1016/j.bmc.2007.07.051

Fan F, Toledo WD, Hamadeh HK, Dunn RT (2019) The integration of pharmacophore-based 3D QSAR modeling and virtual screening in safety profiling: A case study to identify antagonistic activities against adenosine receptor, A2A, using 1,897 known drugs. PLOS ONE 14(1): e0204378; doi:10.1371/journal.pone.0204378

Fourches D, Muratov E, Tropsha A (2010) Trust, But Verify: On the Importance of Chemical Structure Curation in Cheminformatics and QSAR Modeling Research. Journal of Chemical Information and Modeling 50(7): 1189-1204; doi:10.1021/ci100176x

Franco PE (2011) Modelo de multiclasificador basado en selección de rasgos para predecir la afinidad de antagonistas por receptores de adenosina A2B. Tesis de Diploma, Universidad Central Marta Abreu de Las Villas, Santa Clara, Cuba

Gao ZG, Jacobson KA (2007) Emerging adenosine receptor agonists. Expert Opinion on Emerging Drugs 12(3): 479-492; doi:10.1517/14728214.12.3.479

Gaspar A, Reis J, Kachler S, Paoletta S, Uriarte E, Klotz KN, Moro S, Borges F (2012) Discovery of novel A3 adenosine receptor ligands based on chromone scaffold. Biochemical Pharmacology 84(1): 21-29; doi:10.1016/j.bcp.2012.03.007

Gomes MN, Braga RC, Grzelak EM, Neves BJ, Muratov E, Ma R (2017) QSAR-driven design, synthesis and discovery of potent chalcone derivatives with antitubercular activity. Eur J Med Chem 137: 126-138; doi:10.1016/j.ejmech.2017.05.026

González MP, Terán C, Teijeira M (2008) Search for new antagonist ligands for adenosine receptors from QSAR point of view. How close are we? Medicinal Research Reviews 28(3): 329-371; doi:10.1002/med.20108

Hanchuan P, Fuhui L, Ding C (2005) Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence 27(8): 1226-1238; doi:10.1109/TPAMI.2005.159

Hawkins DM (2004) The Problem of Overfitting. Journal of Chemical Information and Computer Sciences 44(1): 1-12; doi:10.1021/ci0342472

Kalash L, Val C, Azuaje J, Loza MI, Svensson F, Zoufir A, Mervin L, Ladds G, Brea J, Glen R, Sotelo E, Bender A (2017) Computer-aided design of multi-target ligands at A1R, A2AR and PDE10A, key proteins in neurodegenerative diseases. Journal of Cheminformatics 9(1): 67; doi:10.1186/s13321-017-0249-4

Kase H (2000) Introductory Remarks: Adenosine A2A Receptor Antagonists. En: Kase H, Richardson PJ, Jenner P (Eds). Adenosine Receptors and Parkinson’s Disease, pp. 1-15. Elsevier, London; doi: 10.1016/B978-012400405-4/50002-2

Khanfar MA, Al-Qtaishat S, Habash M, Taha MO (2016) Discovery of potent adenosine A2a antagonists as potential anti-Parkinson disease agents. Non-linear QSAR analyses integrated with pharmacophore modeling. Chemico-Biological Interactions 254: 93-101; doi:10.1016/j.cbi.2016.05.023

Klotz KN, Hessling J, Hegler J, Owman C, Kull B, Fredholm BB, Lohse MJ (1997) Comparative pharmacology of human adenosine receptor subtypes characterization of stably transfected receptors in CHO cells. Naunyn-Schmiedebergs Archives of Pharmacology 357(1): 1-9; doi:10.1007/PL00005131

Klotz KN, Kachler S, Lambertucci C, Vittori S, Volpini R, Cristalli G (2003) 9-Ethyladenine derivatives as adenosine receptor antagonists: 2- and 8-substitution results in distinct selectivities. Naunyn-Schmiedebergs Archives of Pharmacology 367(6): 629-634; doi:10.1007/s00210-003-0749-9

Lambertucci C, Antonini I, Buccioni M, Ben DD, Kachare DD, Volpini R, Klotz KN, Cristalli G (2009) 8-Bromo-9-alkyl adenine derivatives as tools for developing new adenosine A2A and A2B receptors ligands. Bioorganic & Medicinal Chemistry 17(7): 2812-2822; doi:10.1016/j.bmc.2009.02.030

Lenzi O, Colotta V, Catarzi D, Varano F, Filacchioni G, Martini C, Trincavelli L, Ciampi O, Varani K, Marighetti F, Morizzo E, Moro S (2006) 4-Amido-2-aryl-1,2,4-triazolo(4,3- a )quinoxalin-1-ones as New Potent and Selective Human A3 Adenosine Receptor Antagonists. Synthesis, Pharmacological Evaluation, and Ligand Receptor Modeling Studies. Journal of Medicinal Chemistry 49(13): 3916-3925; doi:10.1021/jm060373w

Michielan L, Bacilieri M, Schiesaro A, Bolcato C, Pastorin G, Spalluto G, Cacciari B, Klotz KN, Kaseda C, Moro S (2008) Linear and Nonlinear 3D-QSAR Approaches in Tandem with Ligand-Based Homology Modeling as a Computational Strategy To Depict the Pyrazolo-Triazolo-Pyrimidine Antagonists Binding Site of the Human Adenosine A 2A Receptor. Journal of Chemical Information and Modeling 48(2): 350-363; doi:10.1021/ci700300w

Michielan L, Bolcato C, Federico S, Cacciari B, Bacilieri M, Klotz KN, Kachler S, Pastorin G, Cardin R, Sperduti A, Spalluto G, Moro S (2009a) Combining selectivity and affinity predictions using an integrated Support Vector Machine (SVM) approach: An alternative tool to discriminate between the human adenosine A2A and A3 receptor pyrazolo-triazolo-pyrimidine antagonists binding sites. Bioorganic & Medicinal Chemistry 17(14): 5259-5274; doi:10.1016/j.bmc.2009.05.038

Michielan L, Stephanie F, Terfloth L, Hristozov D, Cacciari B, Klotz KN, Spalluto G, Gasteiger J, Moro S (2009b) Exploring Potency and Selectivity Receptor Antagonist Profiles Using a Multilabel Classification Approach: The Human Adenosine Receptors as a Key Study. Journal of Chemical Information and Modeling 49(12): 2820-2836; doi:10.1021/ci900311j

Mitchell TM (1997) Machine Learning. WCB/McGraw-Hill Science, London; ISBN: 0070428077

Morales A, Pérez A, Gaspar A, Reis J, Cagide F, Vina D, Cordeiro N, Borges F (2013) Combining QSAR classification models for predictive modeling of human monoamine oxidase inhibitors. European Journal of Medicinal Chemistry 59: 75-90

Moro S, Bacilieri M, Cacciari B, Bolcato C, Cusan C, Pastorin G, Klotz KN, Spalluto G (2006) The application of a 3D-QSAR (autoMEP/PLS) approach as an efficient pharmacodynamic-driven filtering method for small-sized virtual library: Application to a lead optimization of a human A3 adenosine receptor antagonist. Bioorganic & Medicinal Chemistry 14(14): 4923-4932; doi:10.1016/j.bmc.2006.03.010

Müller CE, Jacobson KA (2011) Recent developments in adenosine receptor ligands and their potential as novel drugs. Biochimica et Biophysica Acta (BBA) - Biomembranes 1808(5): 1290-1308; doi:10.1016/j.bbamem.2010.12.017

Mustyala KK, Chitturi AR, Naikal James PS, Vuruputuri U (2012) Pharmacophore mapping and in silico screening to identify new potent leads for A 2A adenosine receptor as antagonists. Journal of Receptors and Signal Transduction 32(2): 102-113; doi:10.3109/10799893.2012.660532

Novellino E, Cosimelli B, Ehlardo M, Greco G, Iadanza M, Lavecchia A, Rimoli MG, Sala A, Da Settimo A, Primofiore G, Da Settimo F, Taliani S, La Motta C, Klotz KN, Tuscano D, Trincavelli ML, Martini C (2005) 2-(Benzimidazol-2-yl)quinoxalines: A Novel Class of Selective Antagonists at Human A 1 and A 3 Adenosine Receptors Designed by 3D Database Searching. Journal of Medicinal Chemistry 48(26): 8253-8260; doi:10.1021/jm050792d

OECD (2004) OECD principles for the validation, for regulatory purposes, of (Quantitative) Structure-Activity Relatinship models. Disponible en: https://www.oecd.org/chemicalsafety/risk-assessment/37849783.pdf. Consultado 28/05/2018

Pérez A (2010) Nuevas aportaciones al desarrollo de modelos QSAR/QSPR para la predicción de la mutagenicidad de contaminantes ambientales y su interacción con sustancias activas presentes en el medio. Tesis de doctorado, Universidad Católica San Antonio, Murcia, España

Pourbasheer E, Shokouhi Tabar S, Masand VH, Aalizadeh R, Ganjali MR (2015) 3D-QSAR and docking studies on adenosine A 2A receptor antagonists by the CoMFA method. SAR and QSAR in Environmental Research 26(6): 461-477; doi:10.1080/1062936X.2015.1049666

Quinlan JR (1993) C4.5 Programs for Machine Learning. Morgan Kaufmann Publishers Inc, San Francisco; ISBN: 1558602402

Quinlan JR (1986) Induction of decision trees. Machine Learning 1(1): 81-106; doi:10.1007/BF00116251

Rahman A (2009) The Role of Adenosine in Alzheimers Disease. Current Neuropharmacology 7(3): 207-216; doi:10.2174/157015909789152119

Roy K, Kar S, Das RN (2015) Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment. Elsevier, London; doi: 10.1016/C2014-0-00286-9

Sheskin DJ (2000) Handbook of parametric and nonparametric statistical procedures. Chapman & Hall/CRC, Boca Raton; ISBN: 158488133X

Sousa JB, Diniz C (2017) The Adenosinergic System as a Therapeutic Target in the Vasculature: New Ligands and Challenges. Molecules 22: 752

Taylor JB, Triggle DJ (2007) Comprehensive Medicinal Chemistry II. Elsevier, London; ISBN: 978-0-08-045044-5

Talete SRL (2010) DRAGON Professional. Disponible en: http://www.talete.mi.it/. Consultado 18/06/2017

Taliani S, La Motta C, Mugnaini L, Simorini F, Salerno S, Marini AM, Da Settimo F, Cosconati S, Cosimelli B, Greco G, Limongelli V, Marinelli L, Novellino E, Ciampi O, Daniele S, Trincavelli ML, Martini C (2010) Novel N 2 -Substituted Pyrazolo (3,4-d) pyrimidine Adenosine A3 Receptor Antagonists: Inhibition of A 3 -Mediated Human Glioblastoma Cell Proliferation. Journal of Medicinal Chemistry 53(10): 3954-3963; doi:10.1021/jm901785w

Taliani S, Trincavelli ML, Cosimelli B, Laneri S, Severi E, Barresi E, Pugliesi I, Daniele S, Giacomelli C, Greco G, Novellino E, Martini C, Da Settimo F (2013) Modulation of A2Badenosine receptor by 1-Benzyl-3-ketoindole derivatives. European Journal of Medicinal Chemistry 69: 331-337; doi:10.1016/j.ejmech.2013.09.001

Todeschini R, Consonni V (2009) Molecular Descriptors for Chemoinformatics. Wiley VCH Verlag GmbH & Co. KGaA, London; doi: 10.1002/9783527628766

Varnek A, Solovev VP (2010) Programa ISIDA (In Silico Design and Data Analysis). Disponible en: http://infochim.u-strasbg.fr/spip.php?rubrique41. Consultado 16/07/2018

Wilson CN, Mustafa SJ (2009) Adenosine Receptors in Health and Disease. Springer, Berlin; doi: 10.1007/978-3-540-89615-9

Witten IH, Frank E, Hall MA (2011) Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann, New Zealand; ISBN: 978-0-12-374856-0

Zhang L, Liu T, Wang X, Wang J, Li G, Li Y, Yang L, Wang Y (2014) Insight into the binding mode and the structural features of the pyrimidine derivatives as human A2A adenosine receptor antagonists. Biosystems 115: 13-22; doi:10.1016/j.biosystems.2013.04.003

Material suplementario

Tabla S1. Resultados de los estadígrafos de los clasificadores por base y por valor de m. (TablaS1.pdf)

Recibido: 18 de Diciembre de 2018; Aprobado: 31 de Enero de 2019

^*Autora para correspondencia e-mail: [e-mail]

Los autores no declaran conflicto de intereses.