ARTÍCULO

 

El análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática

 

The didactic-technological analysis of the teaching-learning process of Mathematics

 

 

M. Sc. Carmen Fortuna González Trujillo,^I Dra. C. Nancy Montes de Oca Recio,^II Ing. Sonia Guerrero Lambert,^III

I. Universidad de Camagüey "Ignacio Agramonte y Loynaz", Cuba [e-mail]
II. Universidad de Camagüey "Ignacio Agramonte y Loynaz", Cuba [e-mail]
III. Universidad de Camagüey "Ignacio Agramonte y Loynaz", Cuba [e-mail]

 

 

---

RESUMEN

El proceso de enseñanza-aprendizaje de la Matemática en la actualidad se encuentra en constantes cambios y transformaciones producto del desarrollo alcanzado por las Tecnologías de la Información y la Comunicación, lo cual reconocen organizaciones internacionales como la UNESCO en sus objetivos priorizados de la agenda para la Educación 2030. No obstante, este proceso en las carreras universitarias de la Universidad de Camagüey "Ignacio Agramonte Loynaz", aún no satisface tales exigencias y aspiraciones, dado por algunas deficiencias, alguna de las cuales están dadas, entre otras causas, por la insuficiente formación de los docentes de Matemática en los contenidos didáctico-tecnológicos ante la ausencia de un marco teórico de referencia desde la Didáctica de la Matemática, lo que se constató, a través de la aplicación de entrevistas y encuestas donde las autoras evaluaron la formación didáctico-tecnológica; de igual forma emplearon el análisis-síntesis y la revisión bibliográfica sobre los marcos teóricos que forman el Enfoque Ontosemiótico (EOS) del conocimiento y la instrucción matemática de Godino et al., el Modelo Teórico del Conocimiento del Contenido Pedagógico Tecnológico (TPACK) de Mishra y Koehler, y el Modelo Teórico del Conocimiento Tecnológico Pedagógico-Práctico Disciplinar (TPACK-PRÁCTICO) de Yeh et al., para construir el marco teórico de referencia que ofrecen las autoras y que sirve de fundamento para el análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática en el siglo XXI.

Palabras clave: didáctica, enseñanza asistida por computadora, enseñanza de la matemática, tecnologías de la información y las comunicaciones.

---

ABSTRACT

The teaching-learning process of Mathematics is currently undergoing constant changes resulting from the achievements of Information and Communication Technologies, that UNESCO has recognized a priority of the agenda for the Education 2030. However, majors at the University of Camagüey "Ignacio Agramonte Loynaz" still fails to satisfy such demands and expectations. This fact, among other causes, is due to insufficient Mathematics teachers' training on the didactic-technological contents, and in the absence of a didactics of mathematics theoretical framework Mathematics Didactics. The authors assessed teachers' the didactic-technological training by given interviews and surveys, as well making use of analysis-synthesis and studying current theoretical frameworks from Godino's Onto-semiotic Approach of knowledge and mathematical instruction, the Theoretical Model of Technological Pedagogical Contents Knowledge of Mishra and Koehler and the Theoretical Model of Technological Pedagogical Disciplinary Knowledge-Practical Disciplinary of Yeh. The study of this framework leads the authors to construct the theoretical frame of reference for the didactic-technological analysis of Mathematics teaching-learning process in the 21st century.

Keywords: didactics, computer-assisted instruction, mathematics instruction, information and communication technologies.

---

 

 

INTRODUCCIÓN

El desarrollo de las Tecnologías de la Información y la Comunicaciones (TIC) que existe en la actualidad trae consigo un replanteamiento de la práctica educativa universitaria, la creación de nuevos ambientes de aprendizajes y una transformación en el desempeño de los docentes universitarios. En este sentido, la UNESCO reconoce en su agenda para la Educación 2030 que "es preciso aprovechar las tecnologías de la información y la comunicación para reforzar los sistemas educativos, la difusión de conocimientos, el acceso a la información, el aprendizaje efectivo y de calidad, y una prestación más eficaz de servicios" (UNESCO, 2015, pág. 4).

En correspondencia con lo anterior, para aprovechar las TIC en función de lograr un aprendizaje efectivo y de calidad, es necesario que los docentes de Matemática que laboran en las carreras universitarias las utilicen desde un enfoque didáctico, a partir de sus potencialidades y posibilidades en el proceso de enseñanza-aprendizaje de la Matemática.

A pesar, de constituir una exigencia en la actualidad la utilización de las TIC en el proceso de enseñanza-aprendizaje de la Matemática, la utilización de los recursos o herramientas tecnológicas como mediadores por parte de los docentes universitarios aún resulta insuficiente. Por tal razón, en el presente artículo científico se propone ofrecer un marco de referencia que sirva de fundamento para el análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática desde el Enfoque Ontosemiótico (EOS) del conocimiento y la instrucción matemática (Godino, Batanero,& Font, 2007), desde el Modelo Teórico del Conocimiento del Contenido Pedagógico Tecnológico (TPACK) (Mishra & Koehler, 2006, 2008) y desde el Modelo Teórico del Conocimiento Tecnológico Pedagógico-Práctico Disciplinar (TPACK-PRÁCTICO) (Yeh, Hsu, Wu, Hwang & Lin, 2014).

 

MÉTODOS

Se aplicaron entrevistas y encuestas a 44 docentes de Matemática que laboran en las carreras universitarias de la Universidad de Camagüey "Ignacio Agramonte Loynaz", de los cuales 16 son doctores que representa el 36,4%, 23 son máster, que representa el 52,3%, cuatro son licenciados, que representa el 9,1% y uno es ingeniero que representa el 2,3%, para indagar sobre la formación didáctico-tecnológica. Se utilizaron la revisión bibliográfica y el análisis-síntesis para la determinación del marco de referencia en el que se sustenta el análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática.

 

RESULTADOS Y DISCUSIÓN

De las entrevistas y encuestas aplicadas a los docentes de Matemática que laboran en las carreras universitarias se constató las insuficiencias en la formación didáctico-tecnológica, las que se manifestaron insuficiencias o carencias de conocimientos relacionados con:

• El empleo de software matemático en el diseño de situaciones de aprendizaje.
• La representación visual en la obtención de la definición de un concepto matemático utilizando las TIC.
• El empleo de las TIC para realizar el tratamiento didáctico de los contenidos matemáticos.
• El dominio de los contenidos didáctico-tecnológicos para la utilización adecuada de las TIC en función de las necesidades de aprendizaje de los estudiantes y de las situaciones de aprendizaje.
• En la evaluación, autoevaluación, coevaluación y heteroevaluación del aprendizaje mediante el empleo de las TIC.

Además, en la revisión bibliográfica realizada se reconoce que entre las barreras que presentan los docentes para utilizar las TIC, se encuentran:

…la falta de experiencia en la enseñanza, las percepciones negativas de la tecnología, el insuficiente tiempo, lugar o el financiamiento para soportar el incremento de los requisitos para que los estudiantes operen con la tecnología en el aula (…)" (Yeh et al., 2014, pág.2).

De los resultados obtenidos anteriormente se reconoce que la integración de las TIC en el proceso de enseñanza-aprendizaje de la Matemática, es una de las cuestiones menos atendidas desde la Didáctica de la Matemática, ya que muchos docentes tienen desconocimiento de los fundamentos epistemológicos de la didáctica desde la visión que se aborda, por lo que desarrollan dicho proceso de forma tradicional sin tener en cuenta las potencialidades y posibilidades que ofrecen las TIC; por otro lado son expresiones que muestran la necesidad de realizar propuestas innovadoras encaminadas a mejorar su análisis didáctico-tecnológico.

A continuación, se ofrecen los resultados de la indagación teórica realizada por las autoras, los que se expresan en los presupuestos teóricos que constituyen el marco de referencia para el análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática y la fase genésica de la investigación en la que se inserta el presente artículo científico, los que manifiestan una carencia o necesidad teórica existente.

Las autoras del presente artículo asumen como presupuesto teórico para el marco de referencia, el Enfoque Ontosemiótico (EOS) del conocimiento y la instrucción matemática (Godino, Batanero & Font, 2007), pues proporciona herramientas teóricas para el análisis didáctico del proceso de enseñanza-aprendizaje de la Matemática. Además, es un sistema teórico que integra otros modelos teóricos usados en la didáctica de la matemática para analizar la actividad matemática, tiene en cuenta la naturaleza de los contenidos matemáticos, el desarrollo cultural y personal; parte de la formulación de una ontología de objetos matemáticos que tiene en cuenta el triple aspecto de la matemática como actividad de resolución de problemas socialmente compartida, como lenguaje simbólico y como sistema conceptual lógicamente organizado(Godino, Batanero & Font, 2009, pág. 4); y brinda herramientas teóricas para analizar conjuntamente el pensamiento matemático (ideas matemáticas), el lenguaje matemático (sistemas de signos),las situaciones-problemas y los factores que condicionan su desarrollo.

La actividad matemática en el EOS ocupa el lugar central y se ha modelado en términos de sistema de prácticas de las que emergen e intervienen los distintos tipos de objetos matemáticos primarios: lenguaje, las situaciones-problemas, los procedimientos, los conceptos, las propiedades y las argumentaciones; a través de los procesos matemáticos comunicación, problematización, definición, enunciación, elaboración de procedimientos y argumentación. Estos objetos se relacionan entre sí formando configuraciones y que según el juego de lenguaje en que participan, se consideran desde las facetas o dimensiones duales: personal-institucional, ostensivo-no ostensivo, expresión-contenido, extensivo-intensivo (ejemplar-tipo) y unitario-sistémico; dando lugar a la tipología de objetos secundarios: personal-institucional, unitario-sistémico, intenso-extensivo, expresión-contenido y ostensivo-no ostensivo; y a los procesos cognitivos/epistémicos: institucionalización-personalización, generalización-particularización,análisis/descomposición-síntesis/reificación,materialización/concreción -idealización/abstracción, y expresión/representación-significación.

En este enfoque se definen algunas nociones teóricas, estás son, práctica matemática como "toda actuación o expresión (verbal, gráfica, etc.) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o generalizarla a otros contextos y problemas (Godino & Batanero, 1994, p. 334); objeto matemático, entendida como "cualquier entidad o cosa a la cual nos referimos, o de la cual hablamos, sea real, imaginaria o de cualquier otro tipo, que interviene de algún modo en la actividad matemática" (Godino, Batanero & Font, 2009, pág. 11); significado, conceptualizado como un "sistema de prácticas matemáticas realizadas por una persona (o compartida en el seno de una institución) ante una cierta clase de situaciones-problemas"(Ídem), y que puede llegar a considerarse como el contenido de cualquier función semiótica; conflicto semiótico, comprendido como "cualquier disparidad o discordancia entre los significados atribuidos a una expresión por dos sujetos (personas o instituciones)"(Godino, Batanero & Font, 2009, pág. 15).

Según este enfoque, los significados pueden ser personal (global, declarado y logrado) si el sistema de prácticas es realizado por una persona; o institucional (implementado, evaluado, pretendido y referencial), si el sistema de práctica es compartida en el seno de una institución. Por otra parte, se amplían los objetos matemáticos primarios al considerar a las situaciones-problemas por ser el origen o razón de ser de la actividad matemática, al lenguaje porque representa a los restantes objetos matemáticos y sirve de instrumento para la acción, y a los argumentos porque justifican los procedimientos y proposiciones que relacionan los conceptos entre sí.

También, en este enfoque se considera que los objetos matemáticos son emergentes del sistema de prácticas matemáticas y que están relacionados entre sí formando configuraciones, que se definen como "las redes de objetos intervinientes y emergentes de los sistemas de prácticas y las relaciones que se establecen entre los mismos. Estas configuraciones pueden ser socio-epistémicas (redes de objetos institucionales) o cognitivas (redes de objetos personales)" (Godino, Batanero & Font, 2009, pág. 8).

En el EOS se considera a la comprensión en términos de funciones semióticas, las que se definen como "una relación entre un antecedente (expresión, significante) y un consecuente(contenido, significado) establecida por un sujeto (persona o institución) de acuerdo con un cierto criterio o código de correspondencia"(Godino, Batanero & Font, 2009, pág. 8), y al proceso de enseñanza-aprendizaje de la matemática como un proceso estocástico multidimensional compuesto de seis subprocesos (epistémico, docente, discente, mediacional, cognitivo y emocional)con sus respectivas trayectorias y estados potenciales y en el que se toma como noción teórica primaria a la configuración didáctica.

La configuración didáctica está "constituida por las interacciones profesor-alumno a propósito de un objeto o contenido matemático y usando unos recursos materiales específicos" (Godino, Batanero & Font, 2009, pág. 12) y lleva asociada una configuración epistémica (una situación-problema, los procedimientos requeridos para su solución, lenguajes, conceptos, proposiciones y argumentaciones, las cuales pueden estar a cargo del profesor, de los estudiantes o distribuidas entre ambos).

De igual forma, la configuración epistémica lleva asociada una configuración instruccional que está constituida por la red de objetos docentes, discentes y mediacionales puestos en juego a propósito del problema o tarea matemática abordada (Ídem). Además, interviene una configuración cognitiva, a través de la cual se describen los aprendizajes que van alcanzando los estudiantes; y una configuración afectiva.

En el análisis del proceso de enseñanza-aprendizaje de la Matemática desde el EOS intervienen también otras nociones teóricas, estas son: norma que se define como "el conjunto de reglas del "juego de lenguaje" en el que participan profesores y alumnos cuando intervienen en un proceso de cognición e instrucción" (Godino, Font, Wilhelmi, & De Castro, 2009, p. 64), e idoneidad didáctica que se define como "la articulación coherente y sistémica de las seis componentes siguientes: epistémica, cognitiva, mediacional, interaccional, emocional y ecológica" (Godino, Batanero & Font, 2009, págs. 14-15).

Las nociones teóricas ofrecidas por el EOS se utilizan en el análisis didáctico del proceso de enseñanza-aprendizaje de la Matemática a través de los siguientes niveles:

1. Análisis de los tipos de problemas y sistemas de prácticas (significados sistémicos).
2. Elaboración de las configuraciones de objetos y procesos matemáticos.
3. Análisis de las trayectorias e interacciones didácticas.
4. Identificación del sistema de normas y metanormas que condicionan y hacen posible el proceso de estudio (dimensión normativa).
5. Valoración de la idoneidad didáctica del proceso de estudio.

Además del EOS del conocimiento y la instrucción matemática, las autoras asumen como presupuesto teórico del marco de referencia, el Modelo Teórico del Conocimiento del Contenido Pedagógico Tecnológico (TPACK)(Mishra & Koehler, 2006, 2008),que hace referencia a las complejas interacciones de las categorías (pedagógico, tecnológico y disciplinar) del conocimiento que el docente necesita en la actualidad para desarrollar un proceso de enseñanza-aprendizaje idóneo con tecnología, donde el conocimiento pedagógico tecnológico y el conocimiento del contenido tecnológico son significativos.

El TPACK parte del Modelo Teórico Pedagogical Content Knowledge (PCK) (Shulman, 1986,1987), que traducido al español es Conocimiento Pedagógico del Contenido (CPC); al que se le integra el conocimiento tecnológico, es decir, se integra la tecnología a la pedagogía, por lo que se basa en la relación entre la tecnología y el proceso de enseñanza-aprendizaje. Este modelo en la práctica toma como base las categorías (figura 1): conocimiento pedagógico (Pedagogical Knowledge, PK), conocimiento del contenido (Content Knowledge, CK) y conocimiento tecnológico (Technological Knowledge, TK); y, a partir de la comprensión de las interacciones en parejas que se dan entre ellas se originan otras tres categorías: conocimiento del contenido pedagógico (Pedagogical Content Knowledge, PCK), conocimiento del contenido tecnológico (Technological Content Knowledge, TCK), conocimiento pedagógico tecnológico (Technological Pedagogical Knowledge,TPK); y de la comprensión de las interacciones de estas tres nuevas categorías se origina la categoría, Conocimiento del Contenido Pedagógico Tecnológico (Technological Pedagogical Content Knowledge, TPACK).

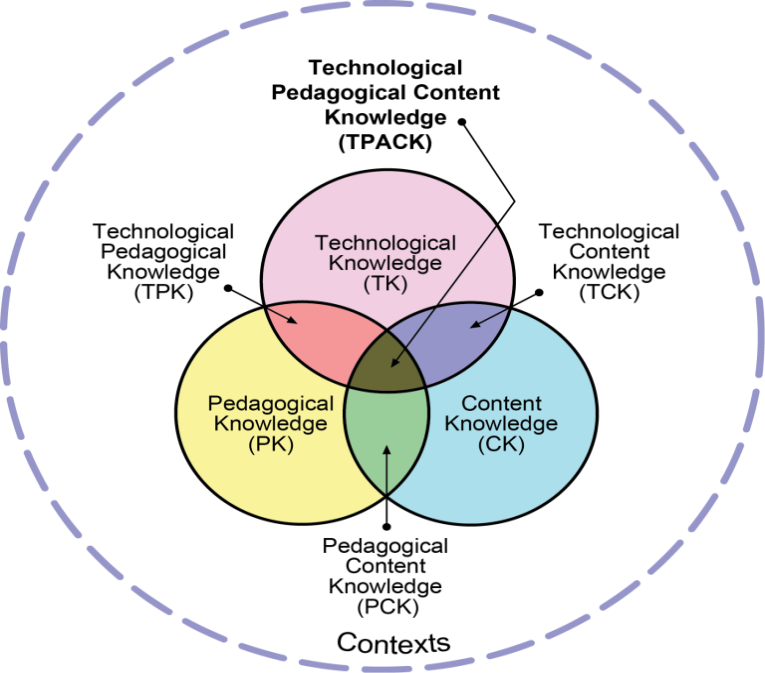
Fig. 1. Modelo TPACK (http://www.tpack.org)

En este modelo se considera al conocimiento pedagógico tecnológico (TPK) como el conocimiento que deben poseer los docentes acerca de "la existencia, los componentes y las capacidades de las diversas tecnologías a medida que se usan en los entornos de enseñanza y aprendizaje y, a la inversa, saber cómo podría cambiar la enseñanza como resultado del uso de tecnologías particulares, que incluye la comprensión de que existe una variedad de herramientas para una tarea en particular, la capacidad de elegir una herramienta basada en su aptitud, las estrategias para usar las herramientas de la herramienta y el conocimiento de estrategias pedagógicas y la capacidad de aplicar esas estrategias para el uso de tecnología (Mishra & Koehler, 2006, p. 1028).

Del mismo modo, se considera al conocimiento del contenido tecnológico (TCK) como el conocimiento que deben poseer los docentes acerca de "la manera en que la tecnología y el contenido están relacionados recíprocamente. Aunque la tecnología restringe los tipos de representaciones posibles, las nuevas tecnologías a menudo ofrecen representaciones nuevas y más variadas y una mayor flexibilidad para navegar a través de estas representaciones. Los maestros necesitan saber no sólo el tema que enseñan, sino también la manera en que el tema puede ser cambiado por la aplicación de la tecnología (Mishra & Koehler, 2006, p. 1028).

Las autoras de este artículo además de asumir el EOS y el TPACK para la elaboración del marco de referencia, también tienen en cuenta el Modelo Teórico del Technological Pedagogical Content Knowledge-Practical (TPACK-Practical), que traducido al español es Conocimiento Tecnológico Pedagógico-Práctico Disciplinar (Yeh, Hsu, Wu, Hwang & Lin, 2014), que parte de asumir los presupuestos teóricos del TPACK y las experiencias prácticas de los docentes desde un enfoque integrativo y transformador, pues consideran que el TPACK que desarrollan los docentes noveles no es el mismo que el desarrollado por los docentes experimentados y la integración de los conocimientos es vista de forma dinámica.

En el TPACK-Practical, sus autores incorporan a las categorías de los conocimientos del docente en el marco teórico TPACK, el conocimiento práctico, pero visto como un conocimiento orientado a la acción, que se basa en la persona y en el contexto. Además, está conformado por ocho dimensiones o categorías (figura 2) agrupadas en cinco áreas pedagógicas en las que los docentes practican la enseñanza con tecnología.

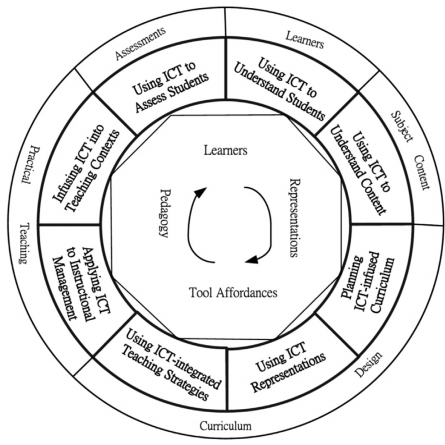
Fig.2. Modelo TPACK-Practical (Yeh, Hsu, Wu, Hwang & Lin, 2014, p. 714)

En la integración de estos marcos teóricos de referencia es donde las autoras connotan el análisis didáctico-tecnológico del proceso de enseñanza-aprendizaje de la Matemática (o también análisis tecnodidáctico-matemático) como se muestra en la figura 3.

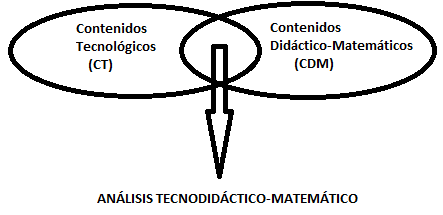
Fig.3. Análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática (elaboración propia, 2017)

Desde esta perspectiva, las autoras aprecian el análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática (o análisis tecnodidáctico-matemático) como el proceso sistémico mediante el cual el docente diseña, implementa y evalúala actividad matemática, basándose en la integración de los contenidos didáctico-matemáticos y los contenidos tecnológicos, a partir de las experiencias prácticas de los docentes y estudiantes.

En este análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática se tendrán en cuenta las variables didáctico-matemáticas, las variables tecnológicas y los niveles de análisis didáctico que ofrece el EOS.

Desde este acercamiento al nuevo marco de referencia sobre el análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática, las autoras consideran que, desde esta nueva perspectiva, consta de los siguientes niveles, pues, en los niveles que ofrece el modelo teórico del EOS sólo se tienen en cuenta las variables didácticas y las variables matemáticas, y en los modelos teóricos TPACK y TPACK-Practical se ofrecen categorías muy generales; sin embargo, en los niveles que ofrecen las autoras, se integran, organizan y extienden las categorías de los contenidos didáctico-matemáticos y de los contenidos tecnológicos que ofrecen los modelos anteriores a los niveles de análisis didáctico que ofrece el EOS y constituyen herramientas teóricas que permiten identificar, clasificar y valorar las tecnologías que facilitan el proceso de enseñanza-aprendizaje de la Matemática.

Identificación de prácticas matemáticas y tecnológicas: En este nivel se exploran: problemas del contexto, situaciones-problemas y los procedimientos requeridos para su solución, lenguajes, conceptos, proposiciones y argumentaciones,y los recursos o herramientas tecnológicas que se van a utilizar en el proceso de enseñanza-aprendizaje de la matemática, los cuales van desde el dominio y comprensión de las TIC en su concepto amplio que abarca tanto las tecnologías tradicionales (libros, pizarra, tiza, etc.), como las tecnologías de avanzada (internet y sus aplicaciones, los dispositivos digitales, la pizarra electrónica, los software educativos, etc.), e incluye las habilidades tecnológicas para navegar por las tecnologías de avanzada y la disposición para realizarlo. Además, este nivel se aplica fundamentalmente al diseño e implementación del proceso de enseñanza-aprendizaje de la Matemática.

Elaboración de las configuraciones de objetos y procesos matemáticos y tecnológicos: En este nivel se tienen en cuenta los objetos matemáticos y tecnológicos, las relaciones que se establecen entre ellos y los procesos matemáticos y tecnológicos, que intervienen en las prácticas matemáticas y tecnológicas, además, de los que emergen de ellas. Su finalidad es describir la complejidad ontosemiótica de las prácticas matemáticas, dada por su significado en el que cada una de las diferentes configuraciones de objetos y procesos posibilita un subconjunto de prácticas. La complejidad ontosemiótica está dada porque el objeto matemático considerado como emergente de un sistema de prácticas, se puede considerar como único y con un significado holístico, pero, en cada subconjunto de prácticas, la configuración de objetos y procesos en las que se presenta el objeto en cuestión es diferente, y por tanto, se posibilitan prácticas diferentes.

Análisis de las trayectorias e interacciones didácticas y tecnológicas: Este nivel se centra en la descripción de los patrones de las interacciones entre los contenidos tecnológicos y los contenidos didáctico-matemáticos y de las relaciones recíprocas entre ellos, y su puesta en relación con los aprendizajes de los estudiantes, en las configuraciones didácticas y su articulación secuencial en trayectorias didácticas. Además, se tiene en cuenta cómo las tecnologías transforman determinada práctica pedagógica y cómo una práctica pedagógica influye sobre determinada tecnología. Aquí se complementan y desarrollan los contenidos tecnológicos y los contenidos didáctico-matemáticos, a partir de sus ventajas y limitaciones.

Identificación del sistema de normas y metanormas: En este nivel se estudian las normas y metanormas que soportan y condicionan las configuraciones y trayectorias didácticas y tecnológicas. Es decir, en este nivel es necesario identificar y describir el conjunto de reglas que regulan las dimensiones (epistémica, cognitiva, mediacional, interaccional, emocional y ecológica) del proceso de enseñanza-aprendizaje de la matemática mediado por las TIC en un contexto institucional determinado, de forma que justifique la adecuada selección de los recursos o herramientas tecnológicas, así como, los fines de su utilización en correspondencia con los contenidos didáctico-matemáticos y los objetivos de aprendizaje pretendidos.

Valoración de la idoneidad didáctica: Este nivel se basa en los cuatro niveles anteriores, los cuales son herramientas para una didáctica descriptiva-explicativa, que integrados con la reflexión de la práctica pedagógica a través de los criterios de idoneidad didáctica propuestos por el EOS: idoneidad epistémica, idoneidad cognitiva, idoneidad interaccional, idoneidad mediacional, idoneidad emocional e idoneidad ecológica, contribuyen a una didáctica descriptiva-explicativa y normativa, yque permiten valorar el proceso de enseñanza-aprendizaje de la Matemática en la actualidad y guiar su mejora. También, se tendrá en cuenta en este nivel el criterio de idoneidad tecnológicapara valorar si las tecnologías que se utilizan contribuyen a mejorar las dificultades de aprendizaje de los estudiantes y si las matemáticas que se enseñan mediadas por las tecnologías son unas "buenas matemáticas".

Además, en este nivel se tiene en cuenta el dominio de los contenidos matemáticos comunes, de los contenidos matemáticos especializados y de los contenidos matemáticos ampliados, así como el dominio de los contenidos didácticos y tecnológicos que se ponen en juego en el proceso de enseñanza-aprendizaje de la Matemática, así como la identificación de los contenidos matemáticos y los contenidos tecnológicos que son necesarios como contenidos previos para su comprensión; la ejecución de las nuevas interrelaciones que se producen entre estudiante-contenido-TIC-docente, estudiante-TIC-contenido, estudiante-TIC-docente y docente-TIC-contenido.

Las autoras consideran que los niveles anteriores permiten realizar el diseño, implementación y evaluación de la actividad matemática desde una perspectiva global en correspondencia con el desarrollo alcanzado por las TIC, forman parte del sistema de categorías de análisis de los contenidos didáctico-matemáticos y tecnológicos que deben poseer los docentes de matemática; para realizar el análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática. También, estos niveles permiten el rediseño de acciones formativas, la formación y desarrollo de competencias profesionales, la evaluación del proceso de enseñanza-aprendizaje de la Matemática y realizar propuestas de mejora. Además, pueden ser empleados como herramientas para el análisis y reflexión de la práctica profesional y para el logro de desempeños idóneos en la actualidad.

 

CONCLUSIONES

A través de la aplicación de los métodos y técnicas científicas que se declararon se pudo constatar la necesidad de un marco teórico de referencia para el análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática.

El análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática consta de los niveles: identificación de prácticas matemáticas y tecnológicas, elaboración de las configuraciones de objetos y procesos matemáticos y tecnológicos, análisis de las trayectorias e interacciones didácticas y tecnológicas, identificación del sistema de normas y metanormas, y valoración de la idoneidad didáctica.

La realización del análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática constituye una necesidad para responder a las exigencias que impone el desarrollo de las TIC en la actualidad.

El análisis tecnodidáctico del proceso de enseñanza-aprendizaje de la Matemática se puede extender a otras ciencias, pues constituye uno de los desempeños de los docentes universitarios en la actualidad.

 

REFERENCIAS BIBLIOGRÁFICAS

Godino, J. D., & Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14(3), 325-355. Recuperado el 10 de mayo de 2017 de http://cimm.ucr.ac.cr/ojs/index.php/eudoxus/article/view/428

Godino, J. D., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. Recuperado el 10 de mayo de 2017 de http://www.ugr.es/~jgodino/funciones-semioticas/ontosemiot

Godino, J. D., Batanero, C., & Font, V. (2009). Un enfoque ontosemiótico del conocimiento y la instrucción matemáticos. Recuperado el 10 de mayo de 2017 de http://enfoqueontosemiotico.ugr.es/documentos/JDGodino_CBatanero_VFont_sintesis_EOS%202009.pdf

Godino, J. D., Batanero, C., Font, V., & Giacomone, B. (2016). Articulando conocimientos y competencias del profesor de matemáticas: el modelo CCDM. En C. Fernández, J. L. González, F. J. Ruiz, T. Fernández, & A. Berciano (Edits.), Investigación en Educación Matemática XX (pp. 288-297). Málaga: SEIEM.

Godino, J. D., Font, V., Wilhelmi, M. R., & De Castro, C. (2009). Aproximación a la dimensión normativa en didáctica de las matemáticas desde un enfoque ontosemiótico. Enseñanza de las Ciencias, 27(1), 59-76. Recuperado el 10 de mayo de 2017 de http://www.raco.cat/index.php/ensenanza/article/viewFile/132207/332991

Mishra, P., & Koehler, M. (2006). Technological pedagogical content knowledge: A Framework for Teacher knowledge. Teachers College Record, 108(6), 1017-1054. Recuperado el 10 de mayo de 2017, de http://punya.educ.msu.edu/publications/journal_articles/mishra-koehler-tcr2006.pdf

Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2). 4-14. Recuperado el 10 de mayo de 2017, de https://www.math.ksu.edu/~bennett/onlinehw/qcenter/shulmanpck86.pdf

Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1). 1-22. Recuperado el 10 de mayo de 2017 de http://hepgjournals.org/doi/pdf/10.17763/haer.57.1.j463w79r56455411

UNESCO. (2015). Declaración de Incheon. Foro Mundial sobre la Educación 2015. Incheon, República de Corea. Recuperado el 10 de mayo de 2017 de http://unesdoc.unesco.org/images/0024/002456/245656s.pdf

Yeh, Y., Hsu, Y., Wu, H., Hwang, F., & Lin, T. (2014). Developing and validating technological pedagogical content knowledge-practical (TPACK-practical) through the Delphi survey technique. British Journal of Educational Technology, 45(4), 707-722. Recuperado el 10 de mayo de 2017 de http://onlinelibrary.wiley.com/doi/10.1111/bjet.12078/pdf

 

 

Recibido: octubre 2017
Aprobado: enero 2018

 

 

González Trujillo es Profesora Auxiliar del Departamento de Educación Ciencias Exactas de la Universidad de Camagüey "Ignacio Agramonte y Loynaz", Máster en la Enseñanza de la Matemática. Es colaboradora del grupo científico para el perfeccionamiento de la Didáctica de la Matemática en las carreras de Ingenierías en la Universidad de Camagüey y pertenece al grupo científico para el perfeccionamiento del modo de actuación profesional de los docentes universitarios desde la formación continua en el contexto de la informatización de la universidad.