INTRODUCCIÓN
La importancia de la función cuadrática en carreras de humanidades se ve reflejada en el desarrollo de modelos matemáticos asociados en esas áreas. Para mostrar esta afirmación Agastya, Bag y Chakraborty, (2014) han realizado investigaciones precedentes como las que corresponden a las funciones de incertidumbre residual cuadráticas en las ciencias de la comunicación y los procedimientos estadísticos utilizados para la predicción de entornos relacionados con la justicia penal (Berk, 2011), entre otros.
En relación a la función cuadrática es necesario tener en cuenta las ideas de pensamiento relacional y covariacional (Ozaltun y Bukova, 2017), además de la coordinación de las distintas representaciones de la función cuadrática (Díaz, Haye, Montenegro y Córdoba, 2015). Sin embargo, en su enseñanza se continúa priorizando la memorización de reglas y propiedades, y el uso de tratamientos algebraicos. En este contexto, diversas investigaciones evidencian la necesidad de incorporar ambientes de representaciones dinámicas en la enseñanza de diferentes dominios matemáticos, como por ejemplo en la enseñanza de las funciones cuadráticas. En ese sentido, Salazar (2015) y Lima (2016) mencionan que la mediación del ambiente de representaciones dinámicas GeoGebra, promueve la construcción función cuadrática y favorece las diferentes representaciones (gráfica, algebraica, etc.) de la función cuadrática de manera dinámica, lo cual facilita que los estudiantes conjeturen sus propiedades inherentes. Además, el GeoGebra también permite analizar y entender la naturaleza variable de la función cuadrática (Ávila, 2011), así como los aspectos: relacional, variacional y de coordinación de representaciones (Minh y Lagrange, 2016).
Desde otra perspectiva, Briceño y Buendía (2015) mencionan que la modelización, en nuestro caso modelización de la función cuadrática, permite vincular la matemática con contextos de otras áreas científicas. Este hecho favorece la enseñanza y el aprendizaje de las matemáticas en carreras de humanidades en las que se presenta mayor dificultad en cuanto a la enseñanza del análisis (Beltrão e Igliori, 2010).
Considerando lo antes mencionado, especificamos que el propósito de la investigación es analizar de manera detallada el trabajo matemático personal de estudiantes de humanidades de un primer curso de matemáticas en una universidad privada de Lima-Perú, cuando movilizan el concepto de función cuadrática al resolver una tarea de modelización con la mediación del GeoGebra. Para ello, nos basamos en los aportes de Almonacid (2018) y de Salazar, Carrillo, Neira-Fernández y Montoya-Delgadillo (2019).
MÉTODOS
Para alcanzar el objetivo planteado nos basamos en la teoría del Espacio de Trabajo Matemático (ETM), desarrollado por Kuzniak (2011) que se estructura en relación a los planos, epistemológico y cognitivo pues esta conexión permite analizar la actividad de un individuo cuando resuelve una tarea matemática.
En el plano epistemológico son tres las componentes que describen el trabajo matemático: un conjunto concreto de objetos tangibles (representamen o signo) que pueden organizarse en sistemas de representación semiótica en el sentido de (citado en Kuzniak, Nechache & Drouhard, 2016), un conjunto de artefactos (artefactos), en el sentido de Rabardel (citado en Kuzniak, Tanguay & Elia, 2016), tales como instrumentos de dibujo, software o algoritmos relacionados a artefactos materiales; y un sistema de referencia (referencial) basado en definiciones, propiedades y teoremas.
En el plano cognitivo se incorpora como componentes la visualización, construcción y prueba o validación. La visualización está relacionada al proceso de descifrar e interpretar señales considerando las interrelaciones, para la construcción de la representación interna (psicológica) de los objetos involucrados y sus relaciones. La construcción está relacionada con acciones provocadas por el uso de artefactos, acciones que pueden no necesariamente resultar en una producción tangible tal como dibujos o escritos, pero bien puede abarcar la observación, exploración o la experimentación. Ello depende de los artefactos utilizados y las técnicas asociadas. La prueba o validación relacionada a los procesos de producción de argumentaciones, basado en un marco teórico de referencia. En relación a las génesis que articulan estos planos se definen: la génesis semiótica, que, definida como un proceso circulatorio entre el representamen y el proceso de visualización, permite, además de exteriorizar las representaciones mentales del individuo mediante la codificación, deducir significados mediante el descifrado e interpretación de signos o representamen. La génesis instrumental definida como el proceso en el cual un individuo transforma un artefacto en instrumento, de acuerdo a sus esquemas de uso. Este proceso es observado en dos sentidos la instrumentación y la instrumentalización que es el proceso inverso, va desde la configuración de la construcción, dirigido por el usuario, hacia la adecuada elección de una herramienta.
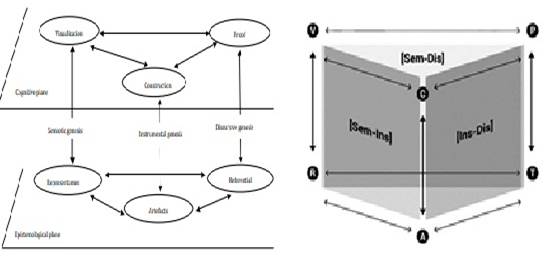
La Figura 1, muestra como la coordinación de las génesis determinan los planos semiótico-instrumental, instrumental-discursivo y semiótico-discursivo, respectivamente. En relación al plano semiótico instrumental [Sem-Ins], en el presente estudio, nos focalizamos en este plano vertical porque le da importancia a la mediación de la tecnología ya que, favorece la exploración de representaciones gráficas de funciones o configuraciones geométricas, con el objetivo de la construcción de conceptos de una noción en particular.
Otro aspecto del ETM es la noción de paradigma. En el dominio del análisis, Montoya-Delgadillo y Vivier (2016) definen los siguientes paradigmas:
Análisis geométrico/aritmético (AG): permite interpretaciones nacidas de la geometría, del cálculo aritmético o del mundo real.
Análisis calculatorio (AC): donde las reglas del cálculo son definidas, más o menos explícitamente, y se aplican independientemente de la reflexión de la existencia y naturaleza de los objetos introducidos.
Análisis Real (AR): es caracterizado por los trabajos que implican aproximación (o una entrada más topológica) (Montoya-Delgadillo y Vivier, 2016, p. 24).
Por otro lado, se distinguen tres ETM: el de referencia, el idóneo y el personal. En el de referencia se guarda relación con el conocimiento, bajo criterios matemáticos; el idóneo depende de la institución involucrada y se define de acuerdo a la forma en que el conocimiento debe ser enseñado, en relación con su lugar y su función específica dentro del currículo nacional; y el ETM personal se relaciona con cada individuo y se define por la forma en que él o ella se ocupa de un problema matemático con sus propios conocimientos y capacidades matemáticas (Kuzniak, Nechache & Drouhard, 2016, p.279). Los autores analizaron el trabajo matemático de los estudiantes en el último.
Además de lo anterior, para alcanzar el objetivo planteado en el presente artículo, fueron tomados en cuenta aspectos de la Ingeniería Didáctica de Artigue (1995), la tarea de modelización fue diseñada sobre función cuadrática, tomando en cuenta el ciclo de modelización de Blum y Borromeo (2009). En relación a los aspectos de la Ingeniería Didáctica, la concepción se da en el diseño de la tarea de modelización sobre función cuadrática que está fundamentada en las investigaciones de referencia (aspectos preliminares) presentadas y en los aspectos del ETM. Luego de tener el diseño de la tarea se procedió con el análisis a priori en el cual se consideraron los posibles procedimientos, respuestas o soluciones que los estudiantes pueden dar en la resolución de la tarea planteada a la luz de los aspectos teóricos y metodológicos empleados. La experimentación se realizó con estudiantes universitarios de primer ciclo (16-18 años) de carreras de humanidades de una universidad privada de Lima, Perú. Se propuso una tarea de modelización organizada en tres fases (tomando en cuenta el ciclo de modelización) que requiere la mediación del GeoGebra. En cuanto a los instrumentos para la recolección de datos, se tienen las fichas de la tarea, los archivos de GeoGebra y fichas de observación. El análisis a posteriori y la validación se inició con la organización y análisis de los datos recolectados. En este proceso se identificaron las estrategias realizadas, los errores evidenciados, las herramientas utilizadas al resolver la tarea en concordancia con la activación de las génesis semiótica e instrumental y el semiótico-instrumental del ETM. Finalmente, se procedió a realizar la validación mediante la confrontación del análisis a priori con el análisis a posteriori del estudio.
RESULTADOS
Se presentan el análisis a priori y a posteriori de la tarea propuesta considerando lo trabajado por un estudiante al que llamaremos Augusto, para mantener su identidad protegida. Cabe señalar que se seleccionó este estudiante porque tiene algunos conocimientos previos sobre función cuadrática, pues este tema es presentado de manera básica en el nivel educativo anterior (nivel secundario en el Perú). A continuación, se presenta la siguiente tarea que llamamos Escenario y que consta de tres fases.
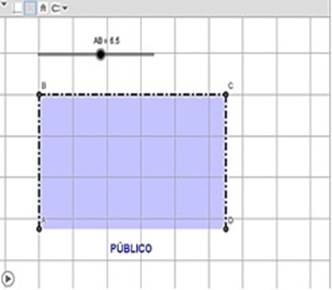
Los estudiantes de un Centro de Música de una universidad peruana, con motivo de la semana de aniversario institucional. Están organizando un concierto, de acceso libre al público. En él, participarán solistas y grupos de hasta ocho integrantes, entre cantantes y músicos. Para para la presentación del concierto se cercará un escenario de forma rectangular (ver Figura 2); pero, no será necesario cercar la parte en frente del público. Además, se sabe que el Centro dispone de tarimas, escaleras y cercas para 24 m de perímetro.
Primera fase: está orientada a la identificación de los valores que intervienen en la tarea, la relación entre ellos y la naturaleza del comportamiento del modelo implícito; además las herramientas y preguntas que se proporcionan restringen el tipo de respuesta que se espera de los estudiantes. A continuación, se presenta lo solicitado: Abra el archivo Escenario_dinámico1.ggb y en la vista gráfica observará la representación del escenario rectangular cercado (verFigura 3).
Se pide que el estudiante responda cada uno de los siguientes ítems:
Arrastre el deslizador “AB” para hacer variar la medida del segmento AB, mencione ¿qué valores cambian y qué valores permanecen contantes? Explique detalladamente.
De los valores mencionados en el ítem i, ¿cuáles son necesarios conocer, para establecer el área del escenario? y ¿por qué no los otros?, justifique.
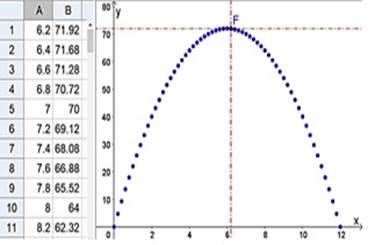
Desde el menú vista abra la hoja de cálculo y utilice el deslizador “AB”, de la vista gráfica, ¿Qué representan los valores de la tabla, en relación con la representación de la vista gráfica? Cuantifica, cómo cambian los valores de la segunda columna cuando la longitud de AB aumenta a razón de 1 ¿Qué relación existe entre estos valores? Explique detalladamente.
Desde el menú vista abra la vista gráfica 2, active la animación con el ícono
 y para detener la animación utilice el ícono
y para detener la animación utilice el ícono , entonces, ¿cómo se relaciona la representación de la Hoja de Cálculo con la representación de la vista gráfica 2? ¿Qué representa el eje X e Y? Explique detalladamente.
, entonces, ¿cómo se relaciona la representación de la Hoja de Cálculo con la representación de la vista gráfica 2? ¿Qué representa el eje X e Y? Explique detalladamente.
Segunda fase: se pregunta lo siguiente: Teniendo en cuenta los datos y las representaciones de la fase 1 determine la expresión matemática que modela el área del escenario, en función de la longitud del segmento AB. Explique detalladamente el procedimiento realizado para hallar dicho modelo.
Tercera fase: se indica lo siguiente: En la barra de entrada de la vista gráfica del GeoGebra ingrese la función algebraica hallada en el ítem anterior y configure ambos ejes, X e Y, en escala de 1:10. Resuelva y justifique. Después de hacer un análisis sobre la cantidad máxima de integrantes e instrumentos que se presentarán en el concierto han concluido que el área del escenario debe medir 70 m2. Este año los encargados de armar el escenario renovarán las cercas de los lados AB y CD, comprarán nuevas cercas, se pregunta: ¿cuáles deben ser las dimensiones del escenario? Si se busca ahorrar en los costos del concierto.
DISCUSIÓN
Los cuatro ítems de la primera fase guían las acciones del estudiante. Es así, que a partir de la manipulación de los artefactos deslizador y cuadricula logra realizar exploraciones y observaciones que le permite conjeturar y validar que el valor que está variando es el área y esta lo hace en función de la medida de la longitud del segmento AB. Estas acciones son evidencia de la activación de la génesis semiótica e instrumental.
Se evidencian dificultades para realizar tratamientos en el registro tabular. Debido a que los procedimientos, en esta fase, se basan en el registro figural y tratamientos aritméticos elementales se evidencia, en el trabajo de Augusto, que prioriza el paradigma del análisis geométrico/aritmético (AG) ya que establece la medida del segmento BC en función del segmento AB, considera las restricciones del valor del segmento AB que le permiten establecer la medida del área de la región rectangular.
La construcción que logra hacer el estudiante (ver Figura 4) le permite descifrar el modelo matemático del área del escenario rectangular en función de la longitud de uno de sus lados. Ejemplo de ello es el resultado expresado en el registro algebraico. En la segunda fase se presenta dos posibles procedimientos, primero toma en cuenta el registro figural y tabular (ver Figura 5).
Y después, como se muestra en la figura 6, utiliza el registro tabular y gráfico para hallar el modelo matemático.
El estudiante Augusto en la primera fase, reconoció que se trata de una función cuadrática, por lo tanto, toma valores de la hoja de cálculo para reemplazarlo en la formula general de una función cuadrática y hallar los parámetros de la misma. La construcción que logra hacer le permite determinar el modelo matemático de la medida del área del escenario rectangular en función de la longitud de uno de sus lados. Ejemplo de ello, es el resultado expresado en el registro algebraico (ver Figura 7).
Las acciones del estudiante evidenciaron la coordinación de la génesis instrumental y semiótica. Los procedimientos basados en la definición general de la función cuadrática y los tratamientos algebraicos muestran que el estudiante prioriza el paradigma del Análisis Calculatorio (AC).
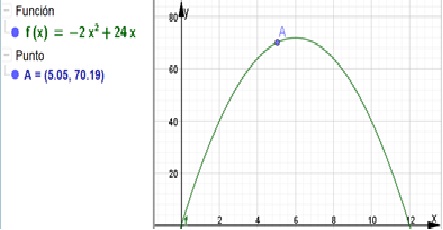
La tarea en la tercera fase está centrada en la validación del modelo matemático y se observa dos tipos de procedimientos, uno basado en la representación gráfica (ver Figura 8) y otro en la representación algebraica de la función cuadrática.
En base a la manipulación del artefacto GeoGebra, el estudiante realiza exploraciones y observaciones, que le permiten conjeturar y validar que la medida del segmento que hace que el área de la región rectangular es 70 m2 es 5m. Sin embargo, el estudiante Augusto no verifica si este es el único caso, tampoco considera la pregunta sobre los costos, realizada en esta fase (ver Figura 9).
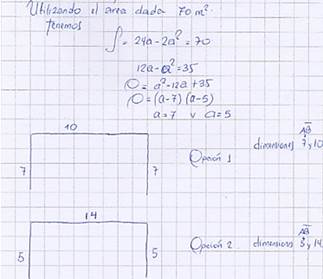
Las acciones de Augusto evidencian que la coordinación de la génesis instrumental y semiótica es parcial al no considerar el análisis de un caso alterno. Los procedimientos basados en el registro gráfico y operaciones aritméticas evidencia que el estudiante prioriza el paradigma del análisis geométrico/aritmético (AG). En el procedimiento basado en la representación algebraica de la función cuadrática. Se observa que el estudiante iguala la expresión algebraica de la función hallada en la segunda fase con la medida del área mencionada y efectúa tratamientos algebraicos que le permiten hallar la medida de la longitud del segmento AB. Sin embargo, similar al caso anterior, no considera la pregunta sobre los costos planteada sobre la situación (ver Figura 10).
Las acciones del estudiante evidencian la coordinación de la génesis instrumental y semiótica, sin embargo, el estudiante no evidencia considerar todas las interrelaciones presentes en la tarea. Los procedimientos basados en el registro gráfico evidencian que el estudiante prioriza el paradigma del Análisis Geométrico/Aritmético (AG).
CONCLUSIONES
Los paradigmas del análisis que en esta investigación el estudiante, al que llamamos Augusto, prioriza cuando realiza la tarea de modelización relacionada a funciones cuadráticas son el Geométrico/Aritmético y el del Análisis Calculatorio (AC).
Respecto a la activación de la génesis semiótica e instrumental y en consecuencia el plano semiótico-instrumental, se evidencia que Augusto logró activarlas al desarrollar la tarea de modelización sobre funciones cuadráticas.
En cuanto al GeoGebra, se observa que este promueve el trabajo matemático personal del estudiante, sobre todo en la segunda y tercera fase de la tarea de modelización