Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
Uno de los objetivos fundamentales de la enseñanza de la Matemática es la resolución de problemas, un tema sobre el que se ha trabajado ampliamente y por consiguiente es abundante la bibliografía especializada sobre el tema, desde los trabajos de Polya (1986) hasta la actualidad se han propuesto innumerables esquemas para dirigir la actividad de los estudiantes con el objetivo de lograr mejorar la eficiencia de los estudiantes en la resolución de problemas. Indudablemente la habilidad de resolver problemas es una necesidad potencial en el campo de la ingeniería y en consecuencia en la formación de las carreras de ciencias técnicas (Darma, 2017).
Hablar de la resolución de problemas en general es un trabajo tan amplio, como la variedad de retos que presenta el aprendizaje de esta disciplina. Por lo que, en aras de concretar un análisis, el presente trabajo se enfoca específicamente a los problemas de optimización en el Cálculo Diferencial de una variable, lo cual viabiliza el análisis de los factores que intervienen en la resolución de este tipo de problemas.
Como se refleja también en la literatura especializada el Cálculo Diferencial presenta dificultades para los estudiantes, las cuales generalmente causan pobres resultados en esa disciplina, motivados, entre otras causas, por el cambio del trabajo con variables estáticas a variables en movimiento que conducen a nuevos tipos de problemas, como los de variación instantánea y los problemas de optimización. De allí que el objetivo del presente trabajo consiste en arribar a la concreción de orientaciones didácticas para el trabajo de los estudiantes con los problemas de optimización, con el fin de influir en su destreza para lograr la mejor opción de resolución; para lo cual se realiza un análisis de las posibles causas que limitan a los estudiantes en este trabajo, entre ellas el uso del lenguaje matemático, el trabajo con las funciones y la transferencia de registros semióticos.
MÉTODOS
Fueron empleados métodos tanto del nivel teórico como del práctico. Los métodos del nivel teórico condujeron a la caracterización del estado del arte y la construcción del marco teórico de la investigación. Del nivel práctico, se empleó el análisis documental, en especial la revisión de los instrumentos de evaluación contestados por los estudiantes para conocer las causas de los errores, así como su correspondencia con lo descrito en la bibliografía especializada.
RESULTADOS
Bases teóricas
Del análisis del trabajo de los estudiantes y la revisión bibliográfica, se pudo precisar causas que limitan el trabajo de los estudiantes con los problemas de optimización, entre ellas el uso del lenguaje matemático, el trabajo con las funciones y la transferencia de registros semióticos. Entre estas causas está presente el carácter sistémico de la Matemática, lo que propicia que sea medio y objeto en sí misma, a su vez implica que la formación precedente de los estudiantes tenga un peso notable en la resolución de los problemas de optimización, ya que se puede decir que toda la formación precedente del estudiante influye en la eficiencia que el estudiante pueda alcanzar en el trabajo con este tipo de problemas. Otro aspecto importante en el tema es la transferencia de registros semióticos (Duval, 2006a), lo que también está en relación con la formación precedente de los estudiantes.
El primer aspecto a analizar aquí es el referido al uso del lenguaje matemático por los estudiantes, dado que el lenguaje matemático se caracteriza por condensar información técnicamente confiable con cierto nivel de abstracción (De Olivera & Cheng, 2011), las palabras del lenguaje coloquial adquieren un significado más preciso, como: límite, monotonía, convergencia, etc. Se trata de un lenguaje en el que no hay sobreentendidos ni ambigüedades, el cual, por ser altamente especializado, está sujeto a una sintaxis muy rigurosa. En general la eficiencia matemática incluye la habilidad de comunicarse y razonar a través del lenguaje escrito y hablado (Riccomini, Smith, Hughes & Fries), 2015).
Los estudiantes en general no interiorizan el lenguaje matemático como una herramienta necesaria para su trabajo en esta disciplina, lo cual evidentemente tiene sus causas en una insuficiente preparación precedente. La necesidad del buen uso del lenguaje se manifiesta desde el mismo inicio de la resolución del problema, pues debe hacerse un cambio del registro literal en el que es presentado el problema, a un registro analítico que en la mayoría de los casos pasa por el registro gráfico. Como se puede apreciar los cambios de representación semiótica también están presentes desde el inicio del proceso de resolución del problema; por lo que es necesario considerar el lenguaje matemático como un sistema de relaciones para establecer significados precisos en la ciencia y también en el contexto didáctico en el salón de clases (Schleppegrell, 2011).
Por ejemplo, en el problema: Encontrar el número positivo x, tal que la suma de x con su recíproco sea la menor posible. El significado de la palabra “recíproco” puede ser entendida como el opuesto aditivo, esto es -x, pero en este caso el alumno debe entender que aquí se refiere al inverso multiplicativo, esto es 1/x.
Otro ejemplo en el que está implícito el buen uso del lenguaje matemático, es el problema conocido como el problema de Tartaglia (1500-1557), cuyo enunciado es el siguiente: “Entre todos los números positivo a y b, cuya suma es 8, encontrar aquellos para los cuales el producto de los dos números y su diferencia sea la mayor posible”. Si el alumno no entiende la “y” como conjuntiva, el cual es su significado en Matemática, puede plantear que lo que se desea optimizar es la expresión: ab + (a - b); pero matemáticamente hablando no hay duda de que se refiere a la expresión: ab(a - b). Pero además el buen uso del lenguaje resulta imprescindible para hacer los necesarios cambios del registro literal al analítico, que por demás en mucho de los casos debe pasar primero a un registro gráfico y después al analítico, como se planteó anteriormente.
Es fundamental destacar la importancia del manejo y buen uso de las relaciones funcionales en el trabajo con los problemas de optimización, dado que las funciones son las herramientas matemáticas para establecer relaciones entre objetos y fenómenos. El concepto de función es, sin lugar a dudas, un elemento fundamental en el trabajo matemático, y ha adoptado a lo largo de su evolución histórica diferentes significados parciales, entre ellos: 1) La función como correspondencia, 2) La función como relación entre magnitudes variables, 3) La función como representación gráfica, 4) La función como expresión analítica, 5) La función como correspondencia arbitraria, y 6) La función a partir de la teoría de conjuntos. Pero es fundamental que los estudiantes comprendan que son diferentes significados de un mismo concepto, expresado en diferentes registros de representación (Amaya, Pino & Medina, 2016). En general, la función es un medio para conectar diferentes representaciones de un objeto matemático.
El trabajo con los problemas de optimización es un momento ideal para entrenar a los estudiantes en la modelación matemática, ya que invariablemente se requiere llegar a un modelo analítico del problema, a través del cual se logra la solución del problema. La modelación matemática está entre los objetivos esenciales de la enseñanza de la Matemática, aunque no siempre se logra desarrollar en los estudiantes las habilidades necesarias para ejecutar esta actividad.
En la bibliografía especializada se encuentran diferentes explicaciones de lo que es un modelo matemático, por ejemplo, se plantea que el proceso de establecer matemáticamente las relaciones y condiciones dadas en un objeto o fenómeno resultan en un modelo matemático y que el proceso que conduce de la situación problema al modelo matemático es lo que puede ser llamado modelación matemática (Jin Hyeong & Kyeong-Hwa, 2016). La modelación puede ser considerada también como una praxeología en el sentido de (García, Gascón, Ruiz & Bosch, 2006), argumentando que el estudio de un proceso, como en este caso la modelación, requiere de un sistema de prácticas.
La vinculación de los contenidos matemáticos con aspectos prácticos objetivos, de la vida real y la necesidad de desarrollar la competencia o habilidad de modelar resulta fundamental en la preparación de los estudiantes (García, et al, 2006). La investigación en relación al universo de modelos tiende a buscar e identificar sistemas apropiados para involucrar a los estudiantes en los procesos de modelación matemática, de modo que les permita alcanzar un nivel adecuado de eficiencia para desarrollar procesos de modelación de modo independiente, aunque hasta el momento no existe una teoría consistente que garantice resultados al respecto.
La resolución de problemas y la modelación matemática, como dos metas importantes en la enseñanza de la Matemática, están en estrecha relación y se complementan mutuamente. Como ya se ha explicado, la resolución del problema generalmente pasa por su modelación, pero la modelación depende en gran medida del uso de las funciones para poder establecer las relaciones matemática implícitas en el fenómeno que se estudia, por ser las funciones las herramientas fundamentales para traducir el lenguaje coloquial al lenguaje analítico. En otras palabras cambiar el registro literal al registro analítico, donde en muchos casos se requiere de una semiótica gráfica para poder llegar a la formulación analítica que permite la resolución del problema.
Lo explicado en el párrafo anterior es inherente a los problemas de optimización, es decir son problemas matemáticos, por lo que en la resolución de problemas de optimización es necesario tener en cuenta los referidos aspectos. Así es que estos problemas, además, tienen características propias que también hay que incluir en el análisis de su proceso de resolución.
Resulta obvio que no se puede aspirar a que el estudiante resuelva estos problemas sin dominar las técnicas del cálculo diferencial, para encontrar los extremos de una función. No obstante, en el presente trabajo se asume que los estudiantes pueden de manera aceptable determinar los extremos de una función, para centrar la atención en los problemas en sí.
La didáctica de la Matemática en los problemas de optimización
Un aspecto que caracteriza los problemas de optimización está dado en que generalmente se debe modelar la función que contiene el valor óptimo solución del problema, la cual usualmente es llamada función objetivo, porque realmente contiene el objetivo a alcanzar para resolver el problema, esta denominación será asumida en el presente trabajo. La función objetivo, en ocasiones, depende de dos o más variables, pero en el problema se pueden encontrar relaciones entre estas variables, las que deben ser expresadas mediante una función que efectivamente enlaza las variables del problema, por lo que es denominada función de enlace. A grandes rasgos, encontrar estas funciones es la vía de solución de los problemas de optimización; pero aquí se presentarán otras precisiones didácticas a tener en cuenta para orientar a los estudiantes.
Es necesario aclarar que, aunque la vía para resolver los problemas de optimización, descrita en el párrafo anterior, es la más usual y caracteriza estos problemas, no es la única, pues en efecto hay casos en que no es la vía idónea, aunque sea aplicable, tal como se ilustra en los ejemplos 1 y 2. La primera precisión didáctica, la cual es aplicable a todo tipo de problema matemático, es el hecho de lograr que los estudiantes interioricen el proceso para resolver un tipo de problema, lo que no quiere decir que hayan adquirido habilidad en la resolución de problemas, cualquiera que sea el tipo de problemas a tratar.
Como es el caso de los problemas donde se plantea que, dada la suma de dos números, encontrar aquellos cuyo producto sea máximo. En los libros de Cálculo Diferencial suelen aparecer variantes de este problema que en esencia se modelan de la misma manera, por lo tanto, que los estudiantes resuelvan varios problemas de este tipo no contribuye a que desarrollen habilidades de modelación. Otro problema que en esencia es del mismo tipo es el referido a encontrar el área máxima de un rectángulo en función de las dimensiones de sus lados, conocido el perímetro. En el primer caso el producto de los números es la función objetivo y la suma la función de enlace; en el segundo caso la función que representa el área es la función objetivo y la expresión del perímetro que relaciona los lados, la función de enlace.
Es oportuno destacar que lo que se critica no es el problema en sí, sino la tipificación del trabajo con los mismos. Este tipo de problema es adecuado como un primer ejemplo, además se puede aprovechar para destacar que no siempre se requiere efectuar la optimización de la función objetivo, ya que en los casos referidos la función que se requiere optimizar es una función cuadrática, el extremo se puede obtener al determinar el vértice de la parábola que dicha función representa. Lo cual es útil desde el punto de vista de la didáctica de la Matemática, al usar contenidos previos, por su contribución a que los estudiantes interioricen la estructura sistémica de la Matemática y propiciar que los estudiantes no mecanicen el proceso.
El que los estudiantes aprecien que en los problemas de optimización no siempre se requieren los procedimientos del cálculo diferencial amplía la visión de los estudiantes sobre las alternativas de resolución de los problemas de optimización, para enfrentar problemas como el siguiente ejemplo:
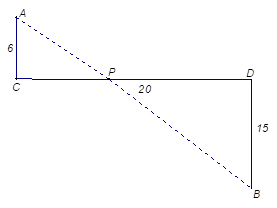
Ejemplo 1: Dos postes uno de 6 metros y otro de 15 metros (figura 1), se encuentran a una distancia de 20 metros, se necesita fijar un tensor en el extremo superior del primer poste y en el extremo superior del segundo poste y fijarlo en el piso, que consideraremos plano, en un punto entre los dos postes, determinar el punto de anclaje de modo que la cantidad de material empleado para el tensor sea la menor posible.
La figura 1 es la materialización en una semiótica gráfica del enunciado literal del problema, es posible naturalmente, determinar la función objetivo a optimizar, pero en este caso resulta más fácil, hacer un cambio de representación semiótica, como se ilustra en la figura 2.
Donde el segmento de recta AB es la menor distancia entre los puntos A y B, luego el punto P es el lugar donde se debe fijar el anclaje en el piso, el cual resulta muy fácil de determinar usando la semejanza entre los triángulos ACP y PDB.
Otro aspecto que también se debe explotar para contribuir a la formación matemática de los estudiantes, es plantear problemas con datos dados en parámetros, en lugar de valores numéricos, de modo que se obtiene un resultado general de la solución del problema. Claro que usando parámetros en lugar de valores numéricos el trabajo algebraico se incrementa, pero los alumnos necesitan ejercitar el tecnicismo algebraico.
El ejemplo 2 ilustra el planteamiento de un problema usando parámetros y además alternativas para resolver el problema sin usar los recursos del cálculo diferencial.
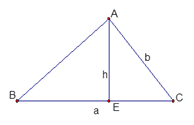
Ejemplo 2: Sea el triángulo ABC con BC = a y CA = b. Si a y b son dados, encuentre un triángulo con área máxima.
En primer lugar, se requiere la materialización semiótica del enunciado literal del problema, como se ilustra en la figura 3.
Conocido que h = b*sen(C) ≤ b; Área(ABC) = a*h/2, como la base a, es un valor dado, el área depende de h, por lo que el área es máxima cuando h es máxima; esto es cuando sen(C) = 1; o sea cuando áng(C) = 90 lo que implica que h = b y por tanto el área del triángulo ABC es máxima cuando es un triángulo rectángulo ya que un cateto coincide con su altura. En este caso, aunque no se usan los recursos del cálculo diferencial para hallar los extremos, sí se requiere de una función de enlace y la función objetivo.
Para una buena formación de los estudiantes es necesario entrenarlos con actividades de demostración y pruebas; se puede decir que muchos estudiantes se asustan cuando el enunciado de la tarea inicia con “demostrar” o “probar que”, por lo que se hace necesario trabajar con este tipo de tareas. Los problemas de optimización también se pueden aprovechar para entrenar a los estudiantes en las demostraciones matemáticas, para lo cual, en muchos casos solo hay que cambiar ligeramente el enunciado del problema, por ejemplo, en lugar de pedir a los estudiantes calcular el rectángulo de mayor área con perímetro igual a 16 cm. Se le puede enunciar el problema como un ejercicio de demostración, esto es: demuestren que de todos los rectángulos de perímetro constante, el de mayor área es el cuadrado.
Otro ejemplo al respecto es: Demostrar que de todos los triángulos isósceles cuyos lados tienen longitud L, el de mayor área es el triángulo rectángulo isósceles. Cuyo proceso de resolución es análogo al ejemplo 2.
Cuando se trabaja el cálculo diferencial en una variable, la generalidad de los problemas de optimización que aparecen en los textos, las condiciones que se plantean relacionan dos variables, pero no necesariamente es así, por lo que para ampliar la visión de los estudiantes sobre estos problemas, se debe plantear algún problema como el siguiente ejemplo.
Ejemplo 3: La suma de tres números positivos es 30. El primero más el doble del segundo, más el triple del tercero suman 60. Elegir los números de modo que el producto de los tres sea el mayor. En el cual, con algo de trabajo algebraico se puede plantear la función objetivo dependiendo de una sola variable.
Otro aspecto importante en el que se debe entrenar a los estudiantes es en el cambio del registro literal al registro gráfico. En los ejemplos anteriores se muestra la ayuda que brinda la representación gráfica para obtener la función objetivo y la función de enlace, pero en muchos casos no es suficiente la simple transferencia del registro literal al registro gráfico, en muchos casos para obtener las ecuaciones necesarias, también se requieren cambios dentro del registro gráfico, dado que cada representación de un fenómeno pone de relieve diferentes aspectos del mismo. En el presente trabajo se asumen, de acuerdo con la teoría al respecto, los cambios dentro de un mismo registro semiótico como tratamiento y de un registro semiótico a otro como conversión (Duval, 2006b).
En el siguiente ejemplo se ilustra lo planteado en el párrafo anterior sobre la necesidad de hacer cambios dentro del registro gráfico (tratamiento):
Ejemplo 4: Hallar las dimensiones del rectángulo de área máxima que se puede inscribir en una circunferencia.
El cambio del registro literal al gráfico, en primera instancia puedes ser como se ilustra en la figura 4 (conversión)
Pero resulta en una considerable simplificación de los cálculos si hace un nuevo cambio de registro semiótico, esta vez dentro del propio registro gráfico (tratamiento), como se ilustra en la figura 5.
Dado que resulta suficiente analizar un cuarto del rectángulo para obtener las dimensiones del rectángulo completo. Resulta necesario que los estudiantes sean capaces de usar la representación semiótica más adecuada, como es el caso cuando se trabaja con un cuerpo volumétrico inscripto en otro.
Otro aspecto importante a considerar en este ejemplo es el uso de asistentes matemático como el GeoGebra, ya que moviendo el punto c se puede inducir cuales deben ser las dimensiones pedidas. Esto permite que los estudiantes puedan apreciar la diferencia entre inducción y prueba, ya que el movimiento del punto puede no permitir la conclusión definitiva, solo el cálculo preciso a través de procedimientos analíticos conduce a la respuesta pedida, pero poder inducir el resultado que se quiere probar es una guía para el trabajo del estudiante y además un paso importante en el desarrollo del conocimiento.
Este ejemplo también es propicio para dar la siguiente orientación de carácter general, en este caso la función objetivo es: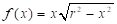 
, pero se puede trabajar con 
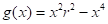, dado que ambas funciones alcanzan el óptimo en el mismo valor de la variable, donde g(x) es el cuadrado de f(x), pero es mucho más cómoda para derivar, situación que se presenta con relativa frecuencia en la resolución de los problemas de optimización.
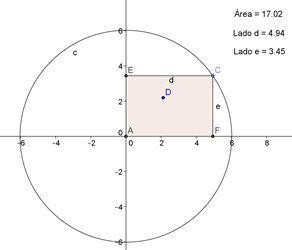
Ejemplo 6: Encontrar el punto de la elipse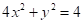 
más alejado del punto (1,0).
A primera vista este problema no aporta nada nuevo respeto a otros ejemplos analizados aquí, pues la función objetivo es 
y usando la ecuación de la elipse como función de enlace se obtiene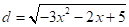 
y tanto esta función como su cuadrado tienen el punto extremo en x = -0.33, pero al evaluar en la ecuación de la elipse para encontrar la ordenada del punto buscado, se obtiene y2 = -3.56 que no tiene solución en los reales, pero usando un asistente matemático se puede inducir la solución, como se ilustra en el siguiente gráfico, figura 6:
Donde se puede apreciar que el punto buscado queda en la rama de la elipse con las ordenadas negativas, por lo que es necesario calcular y2 = 3,56 de donde se obtiene la ordenada de punto buscado y = -1,89.
También es necesario que los estudiantes aprecien las ventajas de usar asistentes matemáticos para ahorrar cálculos algebraicos mecánicos, como en el caso del siguiente ejemplo, que aunque la función objetivo es algo inmediata, implica cierto trabajo algebraico.
Ejemplo 5: determinar el número positivo que sumado con la raíz cuadrada de su recíproco al cubo da una suma mínima.
La función objetivo es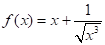 
y su derivada 
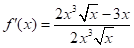; el valor crítico que interesa aquí resulta cuando la derivada se anula, pero en este caso tanto la derivada como los ceros de la misma se pueden obtener usando un asistente matemático, que brindará el resultado x = 1.176; aquí además se debe orientar a los estudiantes que para garantizar que el valor obtenido es un mínimo basta tener en cuenta que la función objetivo tiende a infinito cuando x tiende a cero y cuando x tiende a infinito, por lo que el valor encontrado da un mínimo a la función. Este último procedimiento indicado para determinar el carácter del extremo, no es exclusivo de este problema; esta situación se puede presentar en otros problemas, por lo que es un recurso con el que deben contar los estudiantes.
Resumen de las orientaciones didácticas para el trabajo de los estudiantes con los problemas de optimización
No repetir problemas análogos, plantear problemas con diferentes procedimientos de resolución; los problemas análogos a los resueltos en clase deben ser indicados únicamente como estudio independiente.
Seleccionar los problemas a trabajar en clase para mostrar a los estudiantes diferentes recursos para la resolución de estos problemas.
Plantear problemas donde se pida probar o demostrar, no solo calcular.
Plantear problemas donde no se requieran los procedimientos del cálculo diferencial para su resolución.
Aprovechar cada oportunidad para explicar a los estudiantes la necesidad del buen uso del lenguaje matemático.
Entrenar a los estudiantes en los cambios de registros semióticos (tratamiento y conversión).
Entrenar a los estudiantes en el uso de los asistentes matemáticos: como medio para materializar la representación gráfica de la representación literal del problema, como medio de inducción del resultado, como medio de cálculo para determinar derivadas y ceros de funciones complicadas.
La aplicación por el docente de este conjunto de orientaciones, al tratar los problemas de optimización, propicia que los estudiantes tengan una visión general de una variedad de diferentes situaciones que se pueden presentar en la resolución de este tipo de problemas y además estén al tanto de un conjunto de diferentes alternativas que pueden usar en el trabajo con los mismos, logrando que dispongan de mayores recursos para trabajar con los problemas de optimización.
Ensayo de comprobación
Con el fin de hacer una comprobación de la utilidad de las referidas orientaciones didácticas, se contó con la colaboración de dos docentes con igual experiencia en la impartición del tema y que los resultados de sus estudiantes en los últimos dos cursos no han tenido diferencias significativas en dicho contenido. En el grupo A el docente trabajó según sus criterios personales, tal como lo hizo en cursos anteriores, en el grupo B se le explicó al docente detalladamente las orientaciones a seguir en la explicación del tema, el cual aseguró haber comprendido la idea general y estuvo de acuerdo en su posible utilidad y explicó el contenido según dichas orientaciones.
Por lo tanto, en el grupo B se trabajó iniciando con ejemplos sencillos como es el caso de dada la suma de dos números encontrar los que dan el producto máximo, se continuó con el caso en que se conoce el perímetro de un rectángulo y se desea encontrar el de área máxima. En ambos casos primero con valores numéricos y después con valores paramétricos, sin repetir en clase estos casos, pero dejando ejemplos del mismo tipo para el trabajo independiente de los estudiantes.
Se plantearon problemas sencillos con el enunciado para demostrar como es el caso de demostrar que de todos los rectángulos de perímetro conocido, el de mayor área es el cuadrado, otros problemas de demostrar se reservan para el estudio independiente.
Se plantearon problemas en los que no se requieren las técnicas del cálculo diferencial para encontrar el óptimo, como es el caso del ejemplo 2. Además ejemplos donde es práctico usar los asistentes matemáticos para obtener la derivada y los ceros de la misma, así como las ventajas de usar el cuadrado de la función objetivo como el caso del ejemplo 6.
Siempre se enfatizó el uso de los cambios de representación semiótica, el uso apropiado del lenguaje matemático y de los asistentes matemáticos, tanto para trabajar con funciones objetivo complicadas, como para inducir y comprobar el resultado obtenido analíticamente.
Se pudo comprobar que una vez impartido el contenido en el grupo B según se ha explicado, al comparar las evaluaciones en ambos grupos, las cuales tuvieron el mismo nivel de dificultad, se encontró una diferencia significativa, favorable al grupo B, lo cual permitió apreciar las ventajas de las orientaciones didácticas planteadas para la explicación del tema.
CONCLUSIONES
La resolución de problemas en el presente trabajo ha sido enfocada específicamente a los problemas de optimización. Aunque se tratan aspectos que están presentes de alguna manera en la resolución de problemas en general, como es el caso de los cambios de representación semiótica, la modelación del problema, el buen uso y comprensión del lenguaje matemático como un recurso necesario para el trabajo matemático y la utilización de los asistentes matemáticos, no solo para efectuar cálculos laboriosos, sino también como un medio para inducir y comprobar resultados.
El uso de las relaciones funcionales, aunque es necesario de manera general en el trabajo matemático, en el caso de los problemas de optimización cobra mayor importancia, dada la necesidad de vincular la función objetivo con la función de enlace, para lograr que la función objetivo dependa de una sola variable.
El análisis de los diferentes ejemplos desarrollados permitió arribar al conjunto de orientaciones didácticas, para el trabajo con este tipo de problemas cuya efectividad se pudo comprobar en el ensayo realizado y permite proponer su generalización para el trabajo con este contenido específico. Lo cual permitió el logro del objetivo planteado de influir positivamente en la destreza de los estudiantes para lograr la resolución de los problemas de optimización.
