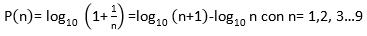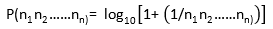Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En el mundo de la investigación científica es necesario la confiabilidad de la investigación y sus resultados, los cuales van a dar cuenta de las aplicaciones en los campos de la vida diaria y sus ciencias aplicadas, esto va a darle transferibilidad a los conocimientos puestos a prueba en las investigaciones, por eso se hace necesario que los mismos sean resultados serios y creíbles, ya que se pondrán en práctica y de allí resultaran exitosos los procesos, erróneos o falsos, trayendo pérdida de tiempo, recursos y hasta posibles pérdidas humanas, lo más grave.
El fraude puede estar presente en cualquier persona que cambie de parecer en cualquier momento de la vida, por cualquier circunstancia que lo motive a hacerlo, esto es completamente impredecible en los seres humanos y cualquier persona puede incurrir en esta falta, aunque nunca se le haya pasado por la mente.
En las investigaciones básicas y aplicadas es necesario el uso del desarrollo científico y tecnológico que generen soluciones a problemas específicos de la sociedad, que al ser investigados y sometidos a pruebas terminan con hallazgos y respuestas a tales planteamientos, dándole rigor científico a dicha experiencia. Por todo lo dicho anteriormente, cabe preguntarse si ¿existirá alguna herramienta científica que permita detectar si existen errores voluntarios o involuntarios en los resultados de una investigación?
Desarrollo
Un fraude es “una acción contraria a la verdad y a la rectitud, que perjudica a la persona contra quien se comete”, según la Real Academia Española (2014). Aunque en la definición el concepto de fraude está asociado con una persona, por extensión esta persona puede ser una compañía o un proceso investigativo, el fraude incluye toda práctica deshonesta llevada a cabo con la intención de causar daño o de privar a otro de sus derechos.
El fraude puede existir en todas las áreas del conocimiento, en empresas, plagios en investigaciones, manipulación de variables y resultados, en la ley, fraude fiscal, electoral, bancario, electrónico, familiar, en la medicina, y en fin donde está involucrado el ser humano como defraudador.
Kroll (2015), presenta un informe a partir de encuestas hechas a altos ejecutivos de diversas compañías sobre el fraude. Se entrevistaron 768 ejecutivos y se concluyó que: el fraude sigue en aumento, el 75% de las compañías informan que han sido víctimas de un incidente de fraude en el último año (2014). Esto significa un incremento del 14% con respecto a la cifra que se informó hace solamente tres años.
Otro estudio sobre fraudes, lo hace Association of Certified Fraud Examiners (2016), donde se analizaron 2410 casos de fraude laboral entre enero de 2014 y octubre de 2015. Los principales hallazgos fueron 6.3 billones de dólares en pérdidas, 23% de los casos ocasionaron más de 1 millón de dólares en pérdidas para la compañía y la pérdida media por caso fue de 150 mil dólares.
Hernández, Llanes & Rodríguez (2007), exponen en su trabajo de investigación que la ocurrencia de algunas manifestaciones impropias en la producción y comunicación de resultados científicos ocurridas en el período 2004-2006, motivó la realización de esta revisión con la intención de profundizar en el conocimiento de las distintas formas en que pueden presentarse estas conductas. Se definen y comentan las formas severas como la fabricación y falsificación de datos, el plagio y otras menores o menos severas que las anteriores, como la publicación duplicada o redundante, autoría injustificada, sesgos de publicación, inexactitud en las citas bibliográficas, entre las más importantes. Se comentan los aspectos éticos de estos problemas y se ofrecen algunos ejemplos de fraudes científicos ocurridos entre 1974 y 2006 que parecieron interesantes exponer.
El matemático y astrónomo Simón Newcomb, en 1881 se percató que las páginas del inicio del libro de logaritmos en su trabajo estaban más viejas y usadas y dedujo que lo dígitos iniciales no tienen la misma probabilidad de ocurrencia, sino que el 1 aparece como dígito más frecuente seguido del 2, hasta el 9 que es el menos frecuente.
Newcomb (1881), enunció verbalmente una relación o ley logarítmica: la ley de probabilidad de ocurrencias de un número es tal que las mantisas de sus logaritmos son equiprobables, Newcom no aportó ninguna explicación matemática para su descubrimiento, lo anotó como una simple curiosidad (Tabla 1).
Tabla 1 Probabilidades para el valor del primer dígito más significativo.
| Dígito d | P(d) | % |
|---|---|---|
| 1 | 0,301 | 30,1 |
| 2 | 0,176 | 17,6 |
| 3 | 0,125 | 12,5 |
| 4 | 0,097 | 9,7 |
| 5 | 0,079 | 7,9 |
| 6 | 0,067 | 6,7 |
| 7 | 0,058 | 5,8 |
| 8 | 0,051 | 5,1 |
| 9 | 0,046 | 4,6 |
Se puede observar que como primer dígito no se toma nunca el 0. Es mucho más probable que el primer dígito sea impar (61%) que par (39%).
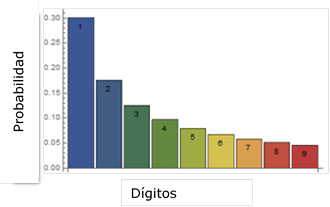
Fue entonces hasta 1938, cuando el físico Frank Benford se dio cuenta del mismo patrón de comportamiento. Estudió 13.779 números de 17 muestras de todo tipo: datos fluviales, constantes, magnitudes físicas y químicas, direcciones de personas, entre otras. Con esos datos determinó la frecuencia de aparición del primer dígito en cada una de las muestras y calculó el promedio de todas juntas. Benford encontró que aun mezclando los datos, que los resultados encajaban en la ley que Newcom que había descubierto años atrás: el 30% empezaban por el número 1, el 18% por 2, el 12% por 3 y así hasta el digito 9. Esto quiere decir, que mientras aumenta el dígito, es menos frecuente que aparezca en el número. Esta ley se puede aplicar a datos relacionados con el mundo natural o con eventos sociales (Fig. 1).
Esta ley está basada en la teoría de las probabilidades y encontró experimentalmente que la probabilidad de que el primer dígito no nulo “n” en una muestra de números extraídos del mundo real aparece con una probabilidad logarítmica.
El primer dígito significativo de un número positivo es el dígito no nulo que aparece más a la izquierda en su expresión decimal. Por ejemplo, el primer dígito significativo de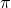
es 3, el de 2371,5 es 2 y el de 0,00563 es 5. Además, concluyó que la probabilidad de los dos primeros dígitos significativos (base 10) satisfacen las siguientes relaciones:
Benford había comprobado las observaciones de Newcom, pero no tenía una explicación sobre estos resultados.
Adicionalmente Pinkham (1961), matemático de New Jersey en 1961, contribuyó a la explicación de los resultados, suponía que debería existir una ley de frecuencias de dígitos y que debería ser universal, indistintamente si miden dólares, colones o yenes, o si se miden longitudes en centímetros, pulgadas, metros o kilómetros (invariabilidad). Todo implica que la distribución de frecuencias de los dígitos debería ser invariable frente al cambio de escala.
Raimi en 1969, fue quien demostró a través de un fundamento matemático la independencia de escala de la Ley de Benford e intenta explicaciones intuitivas de la invariabilidad. En la misma década, fue Theodore Hill quien realizó un trabajo probabilístico para esta ley, extendió la invarianza de escala a invarianza de base e introdujo un nuevo camino para considerar la ley de Benford,
La expresión de la Ley de Benford, establece que la probabilidad de que el primer dígito de una magnitud sea un dígito determinado “n”, es:
Una extensión de la fórmula y generalizada para cualquier conjunto de “n” primeros dígitos es la siguiente:
Se tiene a cada dígito, en función de su posición una probabilidad de ocurrencia. Es decir, la probabilidad del primer dígito 1 es el log [1+ (1/1)] = 0,30 * 100%= 30,1%
La probabilidad de los dos primeros dígitos del par 37, es igual a 
La probabilidad de que los tres primeros dígitos sean la tríada 280 es log [1+ (1/280)] = 0,0015 *100%=0,15%.
Para que sea aplicable la ley de Benford se debe cumplir con ciertas recomendaciones:
Los datos que sigan una secuencia geométrica, que no contenga un máximo, ni un mínimo teórico.
El conjunto de datos debe estar formado por magnitudes medibles de un mismo fenómeno.
La ley de Benford es independiente de la escala de medida en la que se estén trabajando los datos. Los datos no deben ser números determinados y lo ideal es trabajar con datos que registren 4 o más dígitos.
Es recomendable como mínimo 10.000 datos para aplicar la prueba de los 3 primeros dígitos.
La ley de Benford no es aplicable para una serie de números aleatorios porque todos los dígitos tienen la misma probabilidad de ocurrencia.
Por ejemplo, en la ciudad de Quito se crea una nueva calle y esta empieza a llenarse de casas por un extremo, con el tiempo va creciendo en longitud y los primeros portales asignados por el municipio serán 1, 2, 3, etc. se puede observar que la cifra más baja tiene mayor probabilidad de salir que las más altas, cuando se llegue al portal 9 la probabilidad se equilibra, pero al construir el edificio 10, la cifra “1” vuelve a tomar ventaja.
Cuando la calle tenga 19 casas todas las cifras habrán salido 2 veces menos el 1 que habrá salido 12 veces.
Esto ocurre frecuentemente y no se compensa nunca, porque si se escoge una calle al azar, en el número más alto de portal de esa calle es más probable que aparezcan “unos” que “cincos” en una razón que tiende a ley de Benford.
Otro ejemplo, si alguien intenta de falsificar su declaración de impuestos, inventará cualquier dato y al intentarlo, la mayoría de personas tiende a utilizar demasiados números que comienzan por dígitos 5, 6, 7, que pertenecen a la mitad de la escala y pocos que empiezan por 1. Esta violación de la Ley de Benford no implica precisamente fraude, pero sí constituye un buen indicio para justificar una investigación más detallada
La ley se ha propuesto como un posible test de evaluación de resultados obtenidos, ya sea por medios analíticos o de simulación, mediante modelos matemáticos en los que intervienen datos que verifiquen la distribución logarítmica propuesta por la Ley de Benford, como, por ejemplo: en los resultados de elecciones presidenciales y datos fiscales como la declaración de impuesto sobre la renta, detectando posibles situaciones de fallos e irregularidades. La aplicación de ley de Benford ha sido de gran ayuda como herramienta analítica en áreas como las finanzas, auditorías, dimensiones geográficas y sobre todo en la detección de fraudes electorales.
Datos que satisfacen la Ley de Benford
A continuación, se enuncian una serie de variables cuyos datos se han probado y cumplen con la Ley de Benford, entre estos se tienen:
Estadísticas de béisbol.
Constantes y magnitudes físicas y químicas.
Poblaciones.
Pagos de impuesto sobre la renta.
Dimensiones geográficas.
En la desintegración de las partículas radioactivas alfa, se ha encontrado un comportamiento logarítmico que satisface la ley de Benford.
Magnitudes económicas, sociales, entre otras.
Datos que no satisfacen la Ley de Benford.
Los datos que no siguen la Ley de Benford, son los siguientes:
Datos provenientes de distribuciones uniformes (loterías)
Datos sobre edades de las personas (distribuciones normales)
Números telefónicos, datos de identidad
Números procedentes de evaluar funciones cuadráticas, raíces, entre otras.
La ley de Benford se ha aplicado para detectar entrevistadores engañosos. Bredl, Winker, & Kötschau (2008), hicieron cuestionarios en diferentes pueblos de Europa, se definieron variables como número de encuestas por entrevistador, el número de preguntas respondidas y no respondidas. Luego, al aplicar la ley para el primer dígito de estos datos se concluyó que esta es un “buen” punto de partida para detectar posibles fraudes debido a que se encuentran diferencias entre los resultados de un entrevistador honesto y uno que posiblemente está cometiendo fraude; sin embargo, se requieren otras técnicas o análisis adicionales si se desea establecer con certeza si un comportamiento es fraudulento o no
Martínez & Canizalez (2009), en su investigación sobre la Ley de Benford y sus aplicaciones, aplica dicha ley a las a elecciones del Salvador 2004, concluyendo: en general no existe suficientes indicios para dudar de la veracidad de los resultados de las Elecciones Presidenciales de 2004, esto debido a que el análisis del patrón de dígitos solamente es un indicador, el cual permite llevar un estudio más exhaustivo para verificar la presencia o ausencia de fraude; además de existir un buen margen de ganancia por parte del partido ganador.
Hernández (2009), en su trabajo de investigación parte de la pregunta ¿Cómo la Auditoría de Sistemas puede aportar al descubrimiento del fraude en las empresas?, para ello se escogió una empresa en la ciudad de Medellín, que permitió analizar la información de ventas, recaudos, devoluciones entre otros, aplicar la Ley de Benford e identificar irregularidades o fraudes en el proceso de ventas. También se pudo confirmar que la aplicación de esta Ley es efectiva en la identificación de fraude en cualquier empresa. La Ley de Benford, es una herramienta estadística que, a través de la aplicación de las frecuencias, logró demostrar empíricamente que los números tienen un comportamiento regular cuando estos se generan de manera natural. Aplicando esta teoría a varios conjuntos de números, se puede identificar cuáles de éstos cumplen la ley y después de probar en repetidas ocasiones con datos similares el cumplimiento de la ley, se puede inferir que cualquiera de estos conjuntos de datos mantendrá la particularidad del cumplimiento de la ley en los casos normales, cuando no se cumpla, se puede afirmar que hay algo que está alterando los valores, hay un defecto en el proceso o un posible fraude.
Por otra parte, Matute & Zuñiga (2010), desarrollaron un sistema utilizando la Ley de Benford para detectar posibles fraudes electorales en las elecciones convocadas en Ecuador. Concluyen que la ley sirve como referencia para observar manipulaciones o irregularidades en la información y detectar incongruencias en los resultados.
Castañeda (2011), aplicó la Ley de Benford para verificar la viabilidad de aplicar dicha ley al estudio forense en la detección de fraudes electorales, caso particular las elecciones mexicanas del 2006. En éste artículo demuestra que dicha prueba no es una herramienta forense robusta, aplicando a cabo simulaciones de Monte Carlo donde violaciones a la ley de Benford no permite distinguir elecciones limpias y manipuladas.
Breuning & Goerres (2011), en este artículo se dan los resultados de la investigación de las irregularidades electorales en las elecciones del Bundestag de 1990 a 2005 de Alemania unificada sobre la base de la Ley de Benford del segundo dígito (2BL) de Mebane (2008). El análisis consistió en comparar las frecuencias observadas de los numerales de los candidatos y el partido vota a nivel de precinto contra las frecuencias esperadas de acuerdo con Benford. La aplicación de la ley de Benford permitió detectar fraudes sistemáticos en algunos distritos, como en otros no. Esto permitió inferir conclusiones de los diferentes partidos políticos tanto del este de Alemania como del occidente, en cuanto a las votaciones electorales.
Ramírez (2012), en su investigación aplica la Ley de Newcomb - Benford a los resultados de las elecciones presidenciales de Colombia 2010, debido a la inconformidad presentada por un grupo de ciudadanos liderados por Ramírez que identificó fallas e inconsistencias en los procesos de pre-conteo y conteo. Después de aplicar la mencionada ley detectan que la ley tiene ciertas limitaciones matemáticas, por el máximo número de votantes por mesa, en los dígitos 5, 6, 7. 8 y 9 sin embargo, como una medida exploratoria para el análisis y detección de números anómalos fue una primera aproximación a la problemática.
Con Jiménez & Hidalgo (2012), a partir del referendo revocatorio de 2004, un sector importante de la oposición al presidente Chávez ha cuestionado la integridad del sistema electoral venezolano, y pone en duda la legitimidad e imparcialidad de la próxima reunión presidencial del 7 de octubre del 2012.
Negrini (2012), afirmó que esta técnica de la detección de fraudes con la Ley de Benford ha sido aplicada con gran éxito en la oficina fiscal del Distrito de Brooklyn en New York, Estados Unidos
Zamora (2015), aplicó la Ley de Benford para detectar irregularidades o fraudes en el proceso de la declaración del impuesto sobre la renta de la Compañía COINFRA Sociedad Anónima. Zamora pudo confirmar que, al aplicar esta ley a los estados financieros de la empresa en estudio, pudo detectar errores al no cumplir los reportes la tendencia logarítmica de los dígitos de la Ley de Benford, lo que permitió revisar los posibles errores o fraudes, así como hubo estados financieros que sí tuvieron un comportamiento natural o normal y en la revisión de los mismos se detectó el buen procedimiento administrativo que se había aplicado. De la repetida aplicación de la Ley de Benford, pudo inferir que la aplicación de la ley a cualquiera de los estados financieros mantendrá el cumplimiento de la ley en los estados financieros en estudio. Recomienda la aplicación e implementación de la ley en los organismos públicos como privados.
Ballarin (2015), desarrolló un trabajo de investigación donde obtuvo indicios de manipulación contable y posibles prácticas fraudulentas en el gremio del comercio textil de Londres en los siglos XIV y XV mediante técnicas forenses (Ley de Benford) en el periodo 1390-1435. La aplicación de la ley de Benford tanto a la muestra correspondiente a los cobros como pagos, arrojó unos resultados contundentes en cuanto a la existencia de indicios de manipulación contable, así como el rechazo en todos los casos de la hipótesis nula Ho, en el test de las diferencias de chi cuadrado (Ho: La muestra sigue una distribución conforme a la ley de Benford) con un nivel de confianza del 95%.
Cerani & Olivera (2015), realizaron un estudio de la aplicación de la Ley de Benford donde aplicaron un análisis descriptivo e inferencial de la población total en la República Argentina distribuida por departamentos, partidos o comunas, de manera de verificar si el conjunto de 527 datos cumple con la Ley del Primer Dígito. Luego de distintos análisis pudieron llegar a la conclusión de que el conjunto de datos numéricos cumple la Ley de Benford.
Ausloos & Castellano (2016), trabajaron en regularidades y discrepancias de los credit default swaps: una ciencia de datos con enfoque a través de la ley de Benford, en este documento se buscó si la ley de Benford era aplicable para monitorear los cambios diarios en el soberano europeo, las cotizaciones de créditos de incumplimiento crediticio (CDS), que se reconocen como sistemas complejos de contenido económico. El estadístico empleado fue el chi cuadrado, prueba que proporciona una bondad general de medida. Los resultados sugirieron que los contratos más líquidos, parecieron ser la mayoría de los "manipulados". Demostrándose que la Ley de Benford y el chi cuadrado como bondad de ajuste, pudieron detectar la manipulación de datos.
Shi, Ausloos & Zhu (2017), utilizaron la Ley de Benford para hallar las primeras distancias significativas de dígitos y distribución para probar la confiabilidad de los informes financieros en países en desarrollo, encontrando una sospecha común sobre los datos financieros reportados, en 10 sectores industriales de los 6 llamados "principales países en desarrollo" durante el intervalo de tiempo 2000-2014. Estos datos fueron examinados a través de la ley de Benford primer dígito significativo y a través de las pruebas de distancias de distribución.
Los resultados indican que la confiabilidad de los datos es un aspecto obligatorio que debe observarse antes de proceder con análisis y modelado adicionales.
Conclusiones
La Ley de Benford, es una herramienta estadística que, a través de la aplicación de las frecuencias, logró demostrar empíricamente que los números tienen un comportamiento regular cuando estos se generan de manera natural. Aplicando esta teoría a varios conjuntos de números, se puede identificar cuáles de éstos cumplen la ley y después de probar en repetidas ocasiones con datos similares el cumplimiento de la ley, se puede inferir que cualquiera de estos conjuntos de datos mantendrá la particularidad del cumplimiento de la ley en los casos normales o de manera natural, o sea sin alterarlos; cuando no se cumpla, se puede afirmar que hay algo anómalo o posible manipulación de la información recogida en una investigación o fenómeno social.
Lo que se mide es que tanto las frecuencias de los datos se acercan a las frecuencias que están dadas en la Ley de Benford, si están muy desviados, despierta la curiosidad y se pueden acometer para un análisis más profundo en búsqueda de la anomalía presentada que está perturbando los resultados.
Una de las principales aplicaciones de esta Ley está en la detección de fraude, en 1992 se determinó que los datos financieros encajaban perfectamente en la Ley de Benford, lo cual resulta bien importante en la detección de fraude en las finanzas, entre estas, la declaración de impuestos. También es importante su uso en la detección de cambios en las cifras reportadas por Empresas o personas, en años consecutivos, lo cual es útil ya que indicaría que algo puede no andar bien, esta detección temprana ayudaría al ahorro de tiempo y dinero.
En ciertos países latinoamericanos se ha utilizado para detectar fraudes electorales. Como ejemplo, se tiene que en algunos resultados de comicios la distribución de los primeros dígitos, especialmente el segundo, no se ajustaba a la ley de Benford, esto llevó a un reconteo de los votos a fin de verificar los resultados. Por otra parte, científicos belgas han utilizado la ley para la detección de irregularidades en casos clínicos y otros en la verificación de datos demográficos.
Durante muchos años la Ley de Benford fue más que una simple curiosidad estadística sin fundamento matemático alguno ni aplicaciones reales, hoy en día, la ley está firmemente basada en la Teoría de la Probabilidad, goza de un gran interés del público y presenta importantes aplicaciones a la vista de la estadística. Su aplicación se extiende a un gran campo de conjuntos de números, que representan fenómenos de las ciencias aplicadas y naturales.
