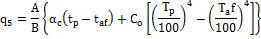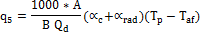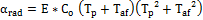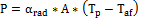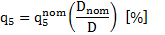Introducción
La eficiencia de un generador de vapor caracteriza la efectividad con que este equipo absorbe la energía liberada por el combustible para la generación de vapor (Horna Paredes, 2019). Durante la producción de vapor existen pérdidas energéticas que ocasionan que este rendimiento disminuya, importante son las pérdidas de calor sensible con los gases de salida (q2) que en calderas del tipo pirotubulares bajo condiciones de cargas parciales oscilan entre un 8 a 30 % y en las del tipo acuatubular son del orden del 8 al 10%, por ello es que resulta importante bajo ciertas condiciones tener la temperatura de los gases lo más baja posible. Otro tanto sucede con la pérdida por radiación (q5), a menudo existen zonas donde se alcanzan temperaturas elevadas debido a la falta de aislamiento térmico o a la insuficiencia de este, llegándose a alcanzar valores de hasta un 5 % o superiores y menores del 2 % en calderas acuotubulares. (Pérez, 2017).
Durante el funcionamiento de los generadores de vapor, las superficies exteriores del horno y los conductos, los colectores, el domo, conductos de gases, tuberías, etc., alcanzan una temperatura superior a la ambiental. Este gradiente de temperatura genera una transferencia de calor al medio exterior que se efectúa por dos mecanismos fundamentales: convección y radiación, lo que representa una pérdida de calor, en ocasiones significativa, que afecta la eficiencia del generador de vapor. A este tipo de pérdidas generalmente se les denomina "pérdidas por radiación", y su magnitud depende fundamentalmente de las dimensiones de la unidad (capacidad nominal), carga y de la temperatura y velocidad del aire exterior (Lapido Rodríguez, et al., 2015).
Las pérdidas por radiación superficial y convección se pueden determinar indirectamente midiendo la temperatura superficial media del generador de vapor y la ambiental próxima a ella (0.5-1.5 m). La temperatura de la superficie, la temperatura ambiente y la velocidad del aire ambiente deben determinarse en un número suficiente de lugares para determinar valores medios representativos; normalmente oscila entre 0-5% de la energía de entrada del sistema. (Mamani, 2018).
La termografía infrarroja como método de mantenimiento predictivo, es un recurso importante en el diagnóstico de problemas y fallas de los equipos muy utilizados en grandes industrias (Xinrui & Memari, 2019; Bolum,et al., 2020). Con la identificación de las fallas previo a las paradas se evitan pérdidas de tiempo en los mantenimientos, ya que con antelación se conoce una serie de información como ubicación y tamaño de deterioros en el material refractario de las paredes de los generadores de vapor o calderas. (Caetano, 2019).
Respecto a los trabajos de supervisión y mantenimiento, la termografía ofrece mayor seguridad ya que permite medir temperaturas a distancia, conservando exactitud y sin tener contacto físico con los objetos a estudiar (Nardi, et al., 2018).
Como parte de las posibilidades que aporta esta técnica se presenta como objetivo principal de este trabajo la integración de ambos aspectos (cualitativos-cuantitativos) para poder determinar las zonas con problemas de aislamiento térmico en un generador de vapor y la cantidad de energía que se pierde en dichas zonas al medio ambiente.
Materiales y métodos
En la literatura Tanquero, et al., (1987); González (2007); y Çengel (2011), presentan diversas expresiones de cálculo para cuantificar la cantidad de calor que pasa al medio según los diferentes procesos de transferencia de calor. En todas existen diferentes variables para caracterizar los procesos de convección y radiación, sin embargo, existe un consenso común en la dependencia directa que existe entre el área, la temperatura superficial, y el valor de estas pérdidas.
Según Tanquero, et al. (1987), las pérdidas por radiación y convección al exterior se determinan mediante la ecuación 1:
Ecuación 1. Pérdidas por radiación y convección al exterior q5. Donde 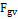 : Área superficial (m2), B: Flujo de combustible (kg/s),
: Área superficial (m2), B: Flujo de combustible (kg/s), 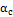 : Coeficiente de transferencia de calor por convección para gases (W/m2.K),
: Coeficiente de transferencia de calor por convección para gases (W/m2.K), 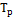 : Temperatura superficial de las paredes (K),
: Temperatura superficial de las paredes (K), 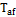 : Temperatura ambiente (K),
: Temperatura ambiente (K),  : Constante de Stefan Boltzmann (W/m2. K4)
: Constante de Stefan Boltzmann (W/m2. K4)
Por otro lado González (2007), presenta para la determinación de la pérdida q5 la ecuación 2:
Ecuación 2. Pérdidas por radiación y convección al exterior q5.
Donde 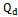 : Calor disponible(kJ/kg),
: Calor disponible(kJ/kg), 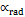 : Coeficiente de transferencia de calor por radiación (W/m2K).
: Coeficiente de transferencia de calor por radiación (W/m2K).
Para el caso de los gases el coeficiente de transferencia de calor por convección 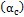 se encuentra en el intervalo de 2-25 W/m2 K (Çengel, 2011). La Constante de Stefan Boltzmann
se encuentra en el intervalo de 2-25 W/m2 K (Çengel, 2011). La Constante de Stefan Boltzmann 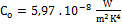 (Çengel, 2011)
(Çengel, 2011)
El coeficiente de transferencia de calor por radiación puede ser determinado mediante la ecuación 3
Ecuación 3. Coeficiente de transferencia de calor por radiación (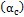 ).
).
Donde E: Emisividad del material del generador de vapor E=0,91
La potencia irradiada en cada una de las zonas críticas se determina mediante la ecuación 4
Ecuación 4. Potencia irradiada en cada una de las zonas críticas.
Existen métodos prácticos para la determinación de la magnitud de estas pérdidas, aunque las mismas podrían determinarse por las ecuaciones convencionales que describen los procesos de transferencia de calor, no obstante, es necesario para ello, la estimación de la temperatura superficial por lo que la medición directa de temperatura permite cuantificar más exacto dicho valor de pérdida. Existe además para la determinación de estas pérdidas fundamentalmente para generadores de mediana y alta capacidad, el método propuesto por la (“American Boiler Manufacturers Association”, ABMA), donde se ha generalizado un nomograma para la estimación de estas pérdidas en función de la capacidad nominal, producción y características de los generadores de vapor. Para cálculos aproximados, González (2007, 2019), presenta para la determinación de la pérdida q5 la ecuación 5, esta se basa en determinar la pérdida de calor por enfriamiento externo para la capacidad nominal de un generador de vapor.
Ecuación 5. Pérdida de calor por enfriamiento exterior (q5).
Donde 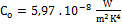 : Pérdida de calor por enfriamiento externo para capacidad nominal (%).
: Pérdida de calor por enfriamiento externo para capacidad nominal (%).
Dnom: capacidad nominal (kg/h), D: Flujo de vapor real (kg/h)
La termografía es un método de medición pasivo que se basa en el estudio de temperaturas de equipos sin necesidad de interrumpir el proceso productivo. Es una técnica relativamente moderna, que se fundamenta en la Ley de Stefan Boltzmann, donde se utiliza la radiación emitida por los cuerpos por estar a temperaturas mayores al cero absoluto, como variable relacionada con la temperatura (Sen & Al-Habaibeh, 2019). Diversas han sido las aplicaciones de esta técnica, la cual por ser no invasiva ha encontrado aplicaciones en los campos de la medicina (Hamlym Jones, et al., 2002), en el análisis de circuitos, como herramienta para el control predictivo (Olarte, et al., 2011) y para diagnosticar temperaturas en paredes de los generadores de vapor (Pérez, et al., 2014).
La tabla 1 presenta las características técnicas de la cámara termográfica modelo testo 875 utilizada para las mediciones de temperatura exterior del generador de vapor.
Tabla 1 - Características técnicas de la cámara termográfica modelo testo 875.
| Medición | Valores |
|---|---|
| Rango | -30 a +100 °C / 0 a +350 °C |
| Exactitud | ±2 °C, ±2 % del valor medido |
| Medición de alta temperatura - opcional | +350 ... +550 °C |
| Exactitud | ±3 % del v.m. a +350 ... +550 °C |
| Emisividad / temperatura reflejada | 0.01 ... 1 / manual |
| Temperatura funcionamiento | -15 ... +40 °C |
| Temperatura almacenamiento | -30 ... +60 °C |
| Humedad del aire | 20 a 80 % HR sin condensación |
| Peso | 900 g |
Para el procesamiento de las imágenes termográficas se utilizó el Software IRISoft. Este permite el manejo de las imágenes a una escala visual con un alto contenido en la calidad de las representaciones, permitiendo también ajustes en la emisividad del material. Con él se pueden ajustar también parámetros en la temperatura reflejada, temperatura ambiente, así como posibilitar perfiles completos de temperatura en una zona a analizar. La temperatura promedio en una zona determinada, el punto más frio o caliente, así como la superposición de la imagen real con la imagen termográfica.
El caso de estudio corresponde a un generador de vapor del tipo pirotubular CMS/C-660 (Figura 1), fabricado en el año 2008. Las características técnicas de este equipo se ofrecen en la tabla 2.
Tabla 2 - Principales características técnicas del generador de vapor pirotubular CMS-660.
| Características | Parámetros |
|---|---|
| Modelo | CMS/C-660 |
| Producción de vapor nominal | 660 kg/h |
| Volumen de agua | 1,90 m3 |
| Superficie de calefacción | 19,6 m2 |
| Presión de diseño | 980,6 kPa |
| Peso de la caldera seca | 3,66 t |
| Peso de la caldera en operación | 5,56 t |
Resultados y discusión
Para el estudio se determinaron a partir de imágenes termográficas, las zonas críticas en la caldera, estas presentaban valores altos de temperaturas donde se evidencia claramente falta de aislamiento térmico.
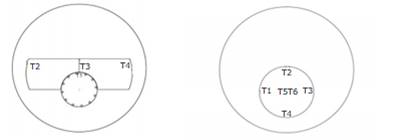
Las mediciones en el lateral de la caldera fueron efectuadas en tres puntos (T1, T2, T3) situados en ambos laterales de la misma (Figura 2). Para el caso de las regiones posterior y frontal de la caldera Figura 3) se consideraron en la primera seis puntos de mediciones (T1...T6), y para el caso de la zona frontal cuatro puntos de mediciones (T1...T4). La tabla 3 ofrece los valores medidos en el generador de vapor, así como la temperatura media en la superficie exterior.
Tabla 3 -Temperaturas medidas en los laterales, zona frontal y posterior del generador de vapor modelo CMS/C-660.
| Puntos | T1 0C | T2 0C | T3 0C | T4 0C | T5 0C | T6 0C |
|---|---|---|---|---|---|---|
| Lateral izquierdo | 57 | 42 | 40 | |||
| Lateral derecho | 40,9 | 46,6 | 38,8 | |||
| Temperatura promedio de la superficie total | 44,21 0C | |||||
| Zona Posterior | 161 | 161 | 138 | 90 | 189 | 171 |
| Temperatura promedio de la superficie total | 151,67 0C | |||||
| Zona Frontal | 186 | 160 | 175 | 160 | ||
| Temperatura promedio de la superficie total | 170,25 0C | |||||
Las temperaturas medidas, ponen de manifiesto que los laterales del generador de vapor presentan de manera general una buena situación en el aislamiento térmico. Las temperaturas medidas en ambos laterales no sobrepasan los 60 0C, donde la temperatura promedio en las superficies laterales fue de 44,21 0C. Las zonas frontal y posterior fueron las zonas con mayores deficiencias detectadas. En la zona frontal se determinó como temperatura promedio 170,25 0C, fundamentalmente en pérdidas que están presente entre las tapas que recubren el haz de tubos de la caldera, mientras que en la zona posterior se alcanzan valores de 150,67 0C detectándose que no existe presencia de aislamiento térmico en la zona central de dicho equipo.
Las áreas críticas se definieron (Tabla 4) a partir del software AutoCAD 2019, el cual permitió la modelación en 2D de cada una de estas zonas y la obtención de las secciones de áreas con el propósito de cuantificar la pérdida de potencia irradiada al medio en ellas, así como las pérdidas por radiación y convección q5.
Tabla 4 - Modelación de las áreas críticas en las zonas frontal y posterior del generador de vapor modelo CMS/C-660.
| Denominaciones | Valores (Zona Frontal) | Valores (Zona Posterior 1) | Valores (Zona Posterior 2) |
|---|---|---|---|
| I1 (mm4) | 283 618x105 | 367 199 x105 | 287 652 x105 |
| I2 (mm4) | 39 197,3x105 | 367 199 x105 | 74 715,4 x105 |
| Sc (mm) | 700 | 465 | 665 |
| St (mm) | 700 | 465 | 665 |
| A (mm2) | 147 234,26 | 679 290,8 | 162 559,93 |
Fig. 4 - Determinación de las áreas de las zonas críticas en mm2 a partir del software AutoCAD 2019.
Donde
I1, I2: |
Momento de inercia centroidal para las zonas críticas. |
Sc, St: |
Posición centroidal para las superficies de las zonas críticas. |
A: |
Área de la sección transversal de las zonas críticas evaluadas. |
El área de la zona crítica frontal estimada mediante AutoCAD fue de 147 234,26 mm2(0,15 m2) (Figura 4) que representa un 8% de la superficie total frontal, y la correspondiente a la zona posterior 841 850,73 mm2 (0,84 m2) (Figura 4).
El análisis termográfico se realizó a la caldera después de esta haber estabilizado su régimen de trabajo en la jornada matutina. En el estudio se realizaron las mediciones termográficas en la parte frontal donde se encuentra el quemador, la zona lateral y la parte posterior (figuras 5, 6 y 7). En cada una de las imágenes se señala una zona crítica. Como criterio para seleccionar cada una de dichas zonas fue considerado que la región tuviera una diferencia superior a los 200C relativo a la zona donde se visualiza una mejor distribución de temperatura. La figura 5 presenta la imagen real y termográfica del frente de la caldera y la zona crítica señalada en color rojo. De manera general la zona frontal presenta buen aislamiento térmico (temperaturas inferiores a los 50 0C), excepto la zona crítica, donde los valores de temperatura exceden los 150 0C. Dicha zona crítica corresponde a los bordes que rodean las tapas del haz de tubos de la caldera, cuya inspección visual coincide con que en dicho lugar no existe aislamiento térmico.
En la figura 6 se presenta la imagen tomada al lateral de la caldera, esta refleja imperfección en las uniones cuando fue colocado el material aislante y que permanecen hasta la fecha. Como se observa en cuatro zonas longitudinales de 0,05 m cada una de espesor alrededor de toda la superficie de la caldera se alcanzan temperaturas en torno a los 60 0C, dichas imperfecciones crean un área total de 1 m2. Una distribución no homogénea de la temperatura en una gran área superficial con diferencias de hasta 250C es la característica fundamental obtenida con la termografía en este plano. Sin embargo, se observan valores superiores a 70 0C en una zona muy pequeña (parte superior derecha figura 5b) que corresponde a la argolla de levantamiento de la caldera que no es de interés para el estudio.
La imagen termográfica de la parte posterior (Figura 6) evidencia donde están las mayores pérdidas de calor por radiación y convección de la caldera en estudio. Con un área crítica que llega a alcanzar el 45% (0,84 m2) de la superficie total de la parte posterior y un valor promedio de temperatura en dicha zona alrededor de los 1750C. Existe un valor tan alto de energía calorífica que hace prácticamente imposible el tacto en la superficie o hasta pasar muy cerca de ella. La figura 7 presenta la imagen real y térmica de la vista posterior del generador de vapor.
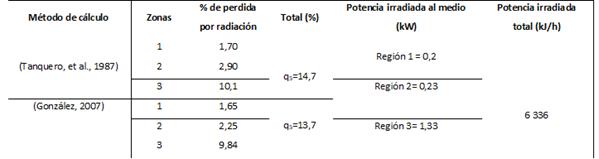
De acuerdo con las ecuaciones 1 y 4 se calcularon las pérdidas de calor por radiación y convección que se producen para cada una de las zonas señaladas como críticas, posteriormente se determinó la cantidad de potencia total irradiada al medio. La pérdida total q5 se estimó como la suma algebraica del % de las pérdidas por radiación en cada una de las zonas. En la tabla 5 se resumen los principales valores obtenidos con el apoyo de la termografía en las zonas con deficiencias en el aislamiento.
El generador de vapor en estudio se encuentra operando de manera general al 50% de su carga nominal. La pérdida total por radiación q5 promedio estimada en las zonas críticas fue de 14,2%, muy superior a la reportado por González (2007), donde reflejan que en zonas donde se alcanzan temperaturas elevadas debido a la falta de aislamiento térmico o a la insuficiencia de este, se llegan a alcanzar valores de q5 hasta un 5 % o superiores. Por otro lado, la tabla 6 refleja la cuantificación por varios autores de la pérdida q5 en generadores de vapor pirotubulares. Para todos los casos dicha pérdida no supera el 4%, siendo notable el desfavorable estado técnico de la caldera en estudio.
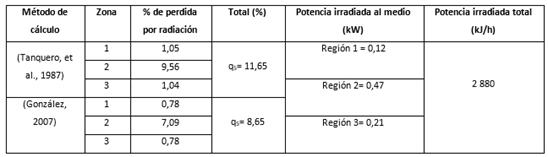
Sin embargo Lapido Rodríguez, et al. (2015), en el estudio Funcionamiento y pérdidas en calderas pirotubulares, para un análisis de 10 calderas de este tipo, refleja que la pérdida por radiación se encuentra entre el 5,32 % y el 14,39%, valores cercanos a lo reportado por Borges, et al., (2016) donde expone un método para la evaluación de la eficiencia energética y el impacto ambiental de un generador pirotubular, estimando la pérdida por radiación en un 13,6% valor similar al obtenido de acuerdo a la ecuación considerada por González (2007). La potencia total irradiada al medio como consecuencia de la ausencia o deterioro en el aislamiento térmico fue de 6 336 kJ/h, esto representa un gasto de energía y combustible diésel. La tabla 7 presenta la cuantificación de las pérdidas de calor por radiación y convección y la potencia irradiada al medio para las zonas no consideradas como críticas de este equipo.
La pérdida por radiación y convección siguiendo la expresión propuesta por Tanquero, et al., (1987) para el caso de las zonas no críticas con relación a las zonas críticas fue de un 20,7% inferior. La diferencia considerando la ecuación de González (2007), fue de 36,9%. Aun con estas diferencias todavía estas pérdidas son muy superiores a lo reportado en la literatura para calderas con un correcto aislamiento térmico. La figura 8 presenta un generador de vapor pirotubular con un aislamiento térmico en su superficie muy eficiente, las temperaturas alcanzadas medidas no superan los 30 0C. La potencia total irradiada al medio obtenida fue de 2 880 kJ/h, un 54,5 % inferior a la irradiada en las zonas críticas. Comparando la zona crítica posterior, la de mayor dificultad en el aislamiento térmico y considerando la superficie de calefacción total en dicha zona (0,84 m2) se obtienen 2 095,2 W/m2 valor crítico muy superior a lo recomendado por Pérez, et al., (2014) de 290 W/m2 y 340 W/m2, a una temperatura ambiente de 25 0C.
Conclusiones
En el estudio se determinaron a partir de imágenes termográficas, los valores de temperatura en las zonas críticas en un generador de vapor del tipo pirotubular modelo CMS/C-660. El valor de temperatura promedio en los laterales, posterior y frontal de dicho equipo fueron de 44,21 0C, 151,67 0C y 170,25 0C respectivamente. Las áreas calculadas con ayuda del software AutoCAD mediante la modelación en 2D fueron de 1m2, 0,84 m2 y 0,15 m2 lo que permitió estimar el por ciento de pérdidas en cada una de estas áreas seleccionadas.
A partir del análisis termográfico con la cámara testo-875 fueron estimadas las temperaturas superficiales que permiten cuantificar las pérdidas por radiación y convección (q5) en las zonas identificadas como críticas y no-críticas mediante dos expresiones de cálculo. Para el caso de las zonas críticas las pérdidas de calor por radiación (q5) fueron de 14,7 % y 13,7 % respectivamente. Sin embargo, estas pérdidas del calor para el caso de las zonas no-críticas fueron un 20,7 % inferiores.
La potencia total irradiada al medio calculada en las zonas críticas considerando la superficie de calefacción fue de 2 095 W/m2 muy superior a lo reportado en la literatura, sin lugar a dudas este valor representa un gasto de energía y combustible, lo que lleva a considerar una correcta insulación térmica que permita disminuir al máximo posible estos gastos y ayude a mejorar el rendimiento del equipo.