Introducción
Una de las mayores dificultades que se presentan en el aprendizaje de las matemáticas en los grados sexto y séptimo, es la construcción del concepto de número negativo, muchas personas pueden considerar que éste, no es un problema tan serio pues se está enseñando uno de los conjuntos numéricos más básicos, sin embargo, no debemos olvidar que, en su momento, una cantidad considerable de matemáticos se resistían a utilizarlos. Fischbein (2002), afirma que los números negativos aparecen en la historia de las matemáticas como una especie de artefacto, como subproductos de problemas matemáticos inadecuados. Además, siempre ha existido una necesidad nunca satisfecha de modelos físicos que logren expresar su naturaleza. En este sentido, los números negativos son quizá el primer ejercicio de abstracción en la vida académica de una persona.
Durante el aprendizaje de los números naturales en la Educación primaria, el estudiante adquiere la concepción de número como cantidad de magnitud con soporte en el mundo físico y concreto. Posteriormente, la generalización de esta concepción a otros campos numéricos supone un obstáculo epistemológico que dificulta su aprendizaje (Herrrera & Zapatera, 2019).
La educación primaria del sistema educativo colombiano no es ajena a esta forma de abordar la enseñanza de los números naturales, desde los primeros años se intenta conceptualizar al número como cantidad, buscando múltiples ejemplificaciones en lo cotidiano, en lo concreto. Sin lugar a duda, esta concepción es tan efectiva y se hace tan profunda en nosotros que es casi inevitable concebir el número fuera del mundo físico. En los estándares básicos de competencias en matemáticas formulados por el ministerio de educación nacional de Colombia se sugiere que un estudiante al terminar el tercer grado de la educación primaria debe saber reconocer “significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización entre otros)”. (Colombia. Ministerio de Educación Nacional, 2003). Y en los derechos básicos de aprendizaje “Identifica los usos de los números (como código, cardinal, medida, ordinal) y las operaciones (suma y resta) en contextos de juego, familiares, económicos, entre otros”. (Colombia. Ministerio de Educación Nacional, 2016) Bajo estas directrices a los maestros del primer ciclo escolar no les queda otro camino sino desarrollar sus prácticas bajo modelos del tipo concreto. Sin embargo, esta práctica que lleva décadas en el sistema educativo colombiano tampoco debe alarmarnos, pues no hace parte del conocimiento público entre los académicos de la enseñanza de la matemática, una investigación que asegure la efectividad de otra concepción netamente formal.
Hasta el momento hemos abordado este problema desde dos enfoques muy relacionados entre sí, pero que sin duda deben tomar caminos diferentes. Referente al proceso histórico del surgimiento de los números negativos y toda la controversia que esto generó dentro de la sociedad matemática, solo hasta mediados del siglo XIX un matemático alemán pudo dar algo de claridad, Hankel (1867), en su afán de una aritmética universal, sustentaba que esto solo iba ser posible en la medida en que se lograra apartarla de percepciones sensoriales, en su libro Hankel refuta los postulados de Peacock (1845), logrando generalizar las propiedades de los naturales también a los números negativos, con lo que finalmente se pudieron formalizar los otros conjuntos numéricos. Por otro lado, desde un enfoque didáctico, el problema sigue vigente, pues el hecho haber logrado una formalización desde la teoría matemática, no significa que también se haya resuelto dicha concepción en la escuela. Esto se puede sustentar con las palabras de uno de los más grandes matemáticos del siglo XX. “Comprendamos, sin embargo, de una vez y categóricamente, lo extremadamente difícil que es, en principio, el paso que se realiza en la escuela cuando se introducen los números negativos”. (Klein, 1925)
Los métodos tradicionales pero efectivos que emplea la escuela primaria para enseñanza de los números naturales, instauran en los estudiantes esquemas mentales profundos que más adelante son una barrera para la concepción y presentación de los números enteros. Parafraseando a González, et al. (1990); Herrera & Zapatero (2019), afirman que “los modelos de tipo concreto no sirven para representar los números enteros, por lo que su enseñanza no es totalmente creíble a través de estos modelos. Sin embargo, también considera que tratarlos desde el aspecto meramente formal tampoco mejora su aprendizaje, ya que son olvidados fácilmente y generan más errores y confusiones a los estudiantes en su actividad matemática. Esta nueva concepción de número genera una ruptura en los procesos de enseñanza y aprendizaje: los estudiantes tienen que cambiar las concepciones que los maestros les inculcaron durante toda la Educación Primaria, y a las que recurrían para lograr comprender las diferentes situaciones que se le planteaban, para ahora buscar la comprensión dentro y desde la matemática”. (p.3)
Al respecto en Brousseau (1983), se concreta que en ocasiones los conocimientos previos se pueden convertir en obstáculos epistemológicos que hacen impiden las construcción de nuevos conocimientos: “Duroux (1983) precisó las condiciones, modificadas después parcialmente por Brousseau (1989), que debe cumplir un obstáculo para ser considerado como epistemológico: un obstáculo epistemológico es un conocimiento que tiene un dominio de validez, que es constitutivo del saber y que persiste y reaparece”. (Herrrera & Zapatera, 2019)
Sin embargo, estos no son los primeros autores en trabajar los obstáculos epistemológicos, Glaeser (1981), ya había planteado algunos obstáculos epistemológicos que se presentan en la enseñanza de los números enteros y los cuales se citan en Herrrera & Zapatera (2019):
Falta de aptitud para manipular cantidades negativas aisladas: aunque se enuncian reglas para efectuar cálculos con números negativos, no se acepta la existencia de números negativos aislados.
Dificultad para dar sentido a las cantidades negativas aisladas: aunque se concibe la existencia de soluciones negativas, no se admiten como cantidades reales.
Dificultad para unificar la recta real: la percepción de negativos y positivos en términos antinómicos impide su unificación en una única recta numérica.
Ambigüedad de los dos ceros: la transición de un cero absoluto, como ausencia de cantidad, a un cero, como origen elegido arbitrariamente, presenta dificultades.
Estancamiento en el estadio de las operaciones concretas: aunque se admite el número negativo como cantidad real y su estructura aditiva, no se justifica la estructura multiplicativa.
Deseo de un modelo unificador: la comunidad matemática está interesada en encontrar un modelo unificador que pueda justificar también la estructura multiplicativa.
Es una dificultad que no se ha podido superar con el paso de los años haciendo que los maestros exploremos diferentes estrategias para abordar estos conceptos de la mejor manera posible. “Las nociones y conceptos que establecen la estructura de los números enteros, en particular la noción de número negativo, presentan dificultades singulares para su aprendizaje y requieren estrategias de instrucción propias durante su enseñanza”. (Bell, 1986)
Por otro lado, la emergencia de salud pública que actualmente enfrenta el mundo, sin lugar a discusión a afectado en gran medida a la educación. Según cifras de Unesco (2020) al menos 190 países se vieron obligados a suspender las clases, se estima que mas de 1.600 millones de estudiantes fracturaron su proceso de aprendizaje por causa de esta emergencia. Los datos de América Latina y el caribe de Comisión Económica para América Latina y el Caribe (2020), reflejan una cantidad considerable de países tomaron medidas de suspensión de clase (Fig. 1).
Algunos de estos países no tuvieron la necesidad de interrumpir su sistema educativo puesto que ya contaban con políticas que aseguraban a sus estudiantes recursos tecnológicos como computadores y tablets, este es el caso de Uruguay. En el caso de Colombia se tomó la medida de adelantar el receso estudiantil para que los maestros tuviéramos tiempo de preparar un plan emergente de una educación virtual y diseñar recursos para aprendizaje a distancia. “Solo 8 de los 33 países contemplan entre las medidas adoptadas para implementar las actividades de aprendizaje a distancia la entrega de dispositivos tecnológicos”. (Comisión Económica para América Latina y el Caribe, 2020)
No es difícil concluir que una de las dificultades más grandes que tuvimos los maestros para lograr dar continuidad al proceso de enseñanza fue las limitaciones de conectividad y dispositivos electrónicos en los hogares de los estudiantes, sobre todo en las zonas rurales del país. Según el estudio hecho en Iberoamérica al preguntarle a los docentes ¿Cuál es el mayor problema ha podido observar en la implementación de modelos de educación virtual en estos momentos de confinamiento? “los el mayor problema encontrado es el desconocimiento de los modelos pedagógicos (27,45%), seguida por la evaluación del alumnado (22,55%), la falta de plataformas tecnológicas (19,60%) sumada a la carencia de recursos tecnológicos (18,63%)” (Fardoun, et al, 2020) pero si se discriminan lo datos por países observamos que las opciones de carencia tecnológica y falta de plataforma en Colombia, tienen números elevados (Fig. 2).
Estas fueron las razones (Fig. 3) que nos llevaron a plantar una estrategia didáctica que pudiera aportar en la deconstrucción del quinto obstáculo epistemológico planteado por Glaeser (1981). En el año 2018 se diseñó y se desarrolló una herramienta móvil para este fin, la herramienta se implementó en la Institución educativa departamental rural Cune en el municipio de Villeta Cundinamarca en el año 2019. Desde la experiencia en el aula se había identificado la dificultad que tienen los estudiantes para la concepción de número negativo, por otro lado, ese estancamiento y la no justificación de la estructura multiplicativa del que habla el quito obstáculo epistemológico de Glaeser se ven reflejados en las habituales confusiones que presentan los estudiantes respecto a la operabilidad de los números enteros, es muy común que los estudiantes opten por la multiplicando signos en el momento de hacer una suma de números enteros. Fue por esta razón que se diseñó y desarrollo la aplicación móvil; los resultados que se obtuvieron en dicha práctica fueron bastantes positivos.
A raíz de la experiencia; teniendo en cuenta los antecedentes, las necesidades de herramientas y plataformas educativas en la actual coyuntura del Covid 19, es bastante coherente preguntarnos: ¿puede un juego móvil diseñado y desarrollado para facilitar el aprendizaje de la adición y sustracción en número enteros, potencializar sus resultados en la modalidad de educación virtual a causa de la actual pandemia?
El uso de la tecnología móvil en entornos de aprendizaje se conoce como mobile learning o más comúnmente como m-learning, desde ya hace varios años se vienen haciendo ejercicios de investigación al respecto, para el caso de Latinoamérica son bastantes las investigaciones que se han realizado en la última décadas, uno de los primeros estudios que podemos encontrar referente al tema en donde se realizan un investigación en un programa de postgrado iniciado en el año 2007, en este estudio se llegaron a resultados importantes que sin duda marcan una linea de investigación importante para la región.
los dispositivos móviles son considerados un recurso adicional de apoyo a los procesos de enseñanza-aprendizaje en el ambiente virtual, donde se busca que el alumno siga siendo el principal constructor de su conocimiento, y los dispositivos móviles un recurso adicional a los que le ofrece su ambiente virtual (Montoya, 2008).
En la ciudad de Monterey, se propone el uso del aprendizaje móvil (m-learning) como herramienta para el desarrollo de habilidades de debate en foros asincrónicos de comunicación (Marcos, et al., 2009; Barros-Bastidas & Gebera, 2020), para la época ya el dispositivo móvil empezaba a considerarse de importancia y necesidad humana, por lo que la educación no pudo ser un escenario ajeno al creciente fenómeno social, desde la innovación académica se empezaba a pensar sobre cómo eran los procesos para la producción de estas herramientas móviles. A partir del año 2010 se empiezan a registrar en Colombia investigaciones sobre herramientas móviles en el entorno educativo, para este año se desarrolla en Medellín un prototipo red social académica que intentaba facilitar la gestión de información entre docentes y estudiantes mediante los dispositivos de tamaño pequeño (smartphone y Tablet) a pesar de las limitaciones tecnológicas (Vázquez & Sevillano, 2015) que tenían en ese momento estos dispositivos, logran un prototipo estable. Herramientas móviles para desarrollar habilidades gramaticales, libros de trabajo digita, entre otros, daban inicio a una nueva linea de investigación en el país.
El constante crecimiento de la tecnología móvil y el acceso a la internet hizo que el desarrollo de las metodologías e-learning (proceso de enseñanza y aprendizaje online) y el m- learning pudieran fusionarse, es así como inicial proyectos que combinan las dos metodologías. Moodle mundialmente conocida como la plataforma por excelencia para la gestión del aprendizaje, para el 2012 ya contaba con un soporte bastante adelantado y una gran acogida por las universidades alrededor del mundo, en la universidad Antonio Nariño de Colombia se trabajaba en la implementación del servicio m-learning combinando tecnologías como Moodle, MySQL, PHP y MLE en una sola plataforma para ofrecerle al usuario la conectividad dentro o fuera del campus desde cualquier dispositivo conectado a la red de internet. Algo muy habitual en la actualidad, pero muy revolucionario en la época. En Wu, et al. (2012), se hace una interesante reseña de estudios realizados entre los años 2003 y 2010, estudiando cerca de 164 investigaciones señalan la importancia del uso de los móviles en la experiencia educativa y recalcan sobre los importantes resultados que estas investigaciones arrojaron. En la Universidad de Oviedo también se realizó un estudio que pretendía elaborar un catálogo de aplicaciones más utilizadas por los universitarios en un rango de edad entre los 18 y los 26 años, entre las conclusiones que arrojó este estudio destaca la importancia de que la comunidad docente acepte una posible incorporación de estos dispositivos móviles en el aula y en el proceso educativo:
Los docentes deben de aprovechar el componente motivacional que actualmente representan estos equipos para los estudiantes, así, el alumnado acepta los dispositivos móviles como un recurso de apoyo tanto para su actividad como para el desarrollo de la docencia por parte del profesorado. Por ello se pueden resumir una serie de beneficios de los dispositivos móviles aplicados a la enseñanza: popularidad, accesibilidad, inmediatez y motivación (Fombona Cadavieco & Pascua Sevillano, 2013).
Importantes universidades ya lograban observar las posibles transformaciones que el desarrollo tecnológico y progresivo del smartphone iba a causar en la educación, un interesante estudio comparativo realizado a estudiantes de universidades españolas e hispanoamericanas reflejaba que “los resultados generales en ambas zonas geográficas muestran que el smartphone se emplea principalmente para el intercambio de información académica, coordinación de trabajos grupales y consulta de servicios universitarios”. (Vasqúez & Sevillano, 2015) la muestra que se utilizó en esta investigación fue de 442 estudiantes españoles y 444 estudiantes hispanoamericanos.
A pesar de las numerosas investigaciones que se pueden encontrar sobre el m-learning alrededor del mundo, Rodríguez Arce & Juárez Pegueros (2017), en su revisión de la literatura concluyen que no existe una clara tendencia acerca de las herramientas móviles como smartphone o tablets dentro y fuera del espacio académico, además aseguran que diversos autores se contradicen en los resultados. Sin embargo, la relevancia del estudio se refleja en la metodología que estos dos autores proponen para el desarrollo y el diseño de aplicaciones móviles, esto a partir de las desventajas que se encontraron en el uso de los m-learning “la falta de desarrollo de habilidades cognitivas necesarias para la tarea de aprendizaje y la incorrecta incorporación de las modalidades de interacción disponibles en los dispositivos de m-learning para favorecer el proceso de enseñanza”. (p.2)
El avance constante que tiene la tecnología móvil es sin lugar a duda, una invitación para que los expertos desarrollo de aplicaciones y docentes hagan equipos de trabajo e investigación que permita también una gama bastante amplia para que los estudiantes puedan mejorar sus procesos de aprendizaje, “la utilidad de tener a disposición amplias colecciones de aplicaciones educativas que permitirán personalizar el aprendizaje de cada estudiante de acuerdo con su interés, mostrando en tiempo real sus avances y dificultades”. (Chiappe & Romero, 2018)
Materiales y métodos
Este proyecto contó con tres etapas comprendidas entre el año 2018 y el al año 2021.Una etapa de diseño y desarrollo de la aplicación móvil (App) otra etapa de implementación que consta de dos fases, la primera fase de implementación con educación en modalidad presencial y otra de implementación en modalidad virtual a causa de la pandemia y una última etapa de evaluación.
Diseño y desarrollo: Anteriormente hemos mencionado las grandes dificultades que se tienen en la concepción de números enteros, adicionalmente a ello existen ciertos obstáculos epistemológicos que dificultan aún más la operabilidad de este conjunto numérico. Herrrera & Zapatera (2019), definen estos obstáculos, en donde se destaca el hecho de que, aun aceptando el número negativo como cantidad real, existe un conflicto entre la estructura aditiva y la estructura multiplicativa, esto es evidente cuando la mayoría de estudiantes al presentarse una adición de números enteros, terminan multiplicando los signos. Bajo esta experiencia surge la necesidad de trabajar estas competencias con una metodología diferente, capaz de abrir una brecha entre estas dos estructuras.
La metodología de diseño que se empleó corresponde a la propuesta que se hace en el artículo de Rodríguez Arce & Juárez Pegueros (2017) en donde se distinguen cinco etapas que inician una vez se define la tarea de aprendizaje, que en nuestro caso es la apropiación de la suma y resta de los números enteros, posteriormente definimos el tipo de habilidades involucradas que a su vez nos llevan a la segunda etapa cuando de cada habilidad identificamos las sub- habilidades primarias y secundarias. El objetivo principal de estas dos primeras etapas es precisamente lograra diagnosticar como podemos incluir en nuestra aplicación los modos de interacción para cada una de las habilidades. Realizada esta tarea podemos diseñar las estrategias para que nuestra herramienta incorpore dichas interacciones y posteriormente poderlas evaluar. En la fig. 4, tomada de Rodríguez Arce & Juárez Pegueros (2017), podemos observar un esquema con la metodología propuesta por los investigadores
Para la fase de evaluación proponen dos etapas compuestas por el análisis de diseño de estrategias y evaluación del caso práctico, los mismos autores Rodríguez Arce & Juárez Pegueros (2017), resumen parte de su propuesta metodológica en la fig. 5.
Es importante destacar que los pasos 5 y 6 de esta etapa nos permiten medir el impacto de la herramienta m-learning: El paso 5 consiste en la evaluación y validación de resultados; en este paso se sugiere contrastar los resultados obtenidos con la estrategia de enseñanza diseñada en los pasos previos en comparación con los resultados obtenidos con un método tradicional (por ejemplo: una presentación por parte del profesor o realizar una lectura). Finalmente, el objetivo de analizar los resultados en la etapa 6 es con la finalidad de establecer la relación entre el tipo de interacciones y el desarrollo de la habilidad en el proceso de aprendizaje (Rodríguez Arce & Juárez Pegueros, 2017).
La herramienta m-learning o aplicación móvil (APP) que recibió el nombre de EnteradoZ y que se puede descargar gratis desde la PlayStore, fue desarrollado mediante el lenguaje de programación HTML 5 y Java Script, la decisión de utilizar dicho lenguaje fue por lo versátil y la función de multiplataforma que nos ofrece esta opción, pues al final vamos a poder tener soporte como aplicación móvil y también como página web. Se elaboraron instrumentos de recolección de datos para que seis docentes del área de matemáticas con experiencia en educación secundaria, identificaran las habilidades y sub-habilidades que se desprenden de la tarea de aprendizaje, en el mismo instrumento se dispuso para propusieran la dinámica del juego, dentro de las características comunes en las respuestas se consideraba que debería ser algo muy sencillo y efectivo, los juegos tipo trivia tienen estas ventajas, son dinámicos y mantienen a los estudiantes activos y concentrados. Con esta idea y siguiendo estrictamente la metodología propuesta para el desarrollo de herramientas m-learning. Se diseño un entorno gráfico sencillo y muy agradable para los estudiantes (Fig. 6).
Fig. 6 - Entorno gráfico de herramienta m-learning diseñada y desarrollada en para esta investigación.
También se elaboraron otros instrumentos de recolección de datos para lograr identificar los errores más frecuentes en dichas operaciones, de esta forma identificábamos también las sub- habilidades de la tarea de aprendizaje que se pretende trabajar (Fig. 7).
Una de las sub-habilidades escogidas por los docentes fue la interpretación gráfica de la operación para trabajar de manera intuitiva esta habilidad se incluyó en el entorno grafico una barra de avance que aumenta o disminuye de acuerdo a los aciertos o desaciertos que tenga el estudiante. Se incluyeron 4 niveles, para pasar al siguiente es necesario que el estudiante tenga 10 aciertos, es decir, que la barra corra 10 veces a la derecha. El primer nivel presenta operaciones entre -20 y 20, el segundo nivel operaciones un poco más grandes entre -50 y 50, el tercer nivel presenta operaciones con tres cantidades y el cuarto nivel ya emplea signos de agrupación.
La implementación del proyecto se llevó en dos etapas, una en el año 2019 de manera presencial y otra en el año 2021 de manera virtual. Implementación presencial: Una vez diseñada y desarrollada la herramienta m-learning se pasó a la etapa de implementación, la población objeto fueron estudiantes de grado séptimo en la institución educativa departamental rural Cune del municipio de Villeta en el año 2019. Los 60 estudiantes estaban divididos en dos grupos de 29 en el gado 701 y 31 en el grado 702.
Con los dos grados se aborda el tema de la misma manera, se les dan las mismas definiciones y los mismos ejemplos, tratando de que esta variable no fuera a incidir en nuestros resultados. Con el fin de hacer un estudio comparativo, a cada uno de los grados se le aplica una metodología diferente en el momento de hacer que los estudiantes practiquen las operaciones de adición. Al grado 702 se les aplica una metodología tradicional, ejemplos y algunos ejercicios para que practiquen.
Con grado 701 se implementa herramienta m-learmimg, a los estudiantes que cuentan con celulares se les instala la aplicación, para hacer que la actividad fuese dinámica, se divide al curso en 6 grupos homogéneos, en cada grupo había al menos un estudiante con celular y la aplicación. Se les presenta el juego mediante la proyección en un televisor, su entorno gráfico, el objetivo, las oportunidades, etc. Luego cada grupo se empieza a preparar para la competencia, que consistía en que cada integrante iba pasando a responder una pregunta y se registraba el tiempo y el nivel al que llegaban. Mientras un grupo participaba los otros estudiantes practicaban en sus celulares o seguían el juego de sus compañeros en el televisor.
Implementación en modalidad virtual: A pesar de las limitaciones, técnicas y tecnológicas que pueden tener los estudiantes de las zonas rurales del país, más del 90 % de los estudiantes de la IEDR Cune cuentan con acceso a WhatsApp en algún momento del día. Naturalmente, no es nada fácil asegurar un proceso cuyo único acompañamiento se puede hacer mediante herramienta de mensajería instantánea.
Al realizar la prueba diagnóstica a los estudiantes del grado octavo de la institución al inicio del año escolar 2021, se puedo evidenciar serios problemas en adición y sustracción de números enteros, se decidió implementar la herramienta con este nuevo grupo a pesar de las dificultades que podían llegar a presentarse. Inevitablemente la población se iba a dividir en dos grupos, los estudiantes que podían descargar el juego de PlayStore y los estudiantes que no iban a tener acceso a internet, nuevamente podíamos hacer un estudio comparativo con estas dos poblaciones (Fig. 8).
A casi 37% de los estudiantes que no lograron el acceso al juego se les implemento otra actividad, por medio de un vídeo corto se les dio la instrucción y se les entrego algunos ejercicios para que practicaran, al otro 63,4 % de la población se les pudo como actividad crear un vídeo en donde se grabaran jugando, llegando mínimo hasta el nivel 2 del juego.
Evaluación: Para esta fase se realizó una evaluación con el fin de contrastar l los resultados entre los estudiantes que utilizaban la herramienta m-learning en la práctica de adición y sustracción de números enteros y los que simplemente recibían un taller de ejercicios para que practicaran, esto siguiendo las recomendaciones que planteaba la metodología propuesta (Fig. 9).
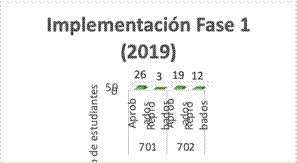
Como podemos observar en el grafico el 89,6% de los estudiantes en el grado 701 en donde se implementó la herramienta m-learning aprobaron la evaluación que se realizó. Solo el 10,4% no lograron el total de las competencias.
Por otro lado, los resultados obtenidos en la fase 2 de implementación nos muestras que el 100% de los estudiantes que lograron obtener acceso al juego aprobaron la evaluación, por otro lado, de los estudiantes que no lograron tener acceso al juego, solo el 71,4% de los estudiantes logra aprobar y por lo tanto el 28,6% reprueban (Fig. 10).
Resultados y discusión
Para lograr dar respuesta a nuestra pregunta de investigación utilizamos el método estadístico de prueba de hipótesis para diferencia entre porciones, ya que las características de nuestra población y los distintos datos que podemos obtener nos brindan la confianza teórica.
Como el objetivo era medir si la implementación de la herramienta m-learning en la modalidad a virtual a causa de la actual pandemia fue más efectiva, observamos que el porcentaje de éxito para la fase 1 fue de p1=26/29=0,896 mientras que para la fase 2, p2=26/26=1, con lo que se plantea las hipótesis (F1).
(F1)
obtenemos ahora porcentaje de fracaso q_1=0,104 y q_2=0 respectivamente. Dada que para este caso las muestras son menores que 30, usamos la distribución de probabilidad t - student con grados de libertad v_1=29-1=28 y v_2=29-1=27 así los grados de libertar generales serán v=28+27-2=53. Con los anteriores datos podemos ahora si aplicar el estadístico de prueba t (F2).
(F2)
Con los grados de libertad y con un nivel de significancia de 5% encontramos un tc=-1,644
Observamos que el estadístico de prueba (Fig. 11) cae en la zona de rechazo (linea roja) por lo que podemos concluir que se rechaza la hipótesis nula y se acepta la hipótesis alterna, esto significa que si podemos afirmar que a un nivel de significancia del 5% el porcentaje de éxito en la segunda fase fue mayor.
Si bien los resultados que obtuvimos en esta investigación y la metodología utilizada para la medición nos podrían responder la pregunta de investigación, es prudente y necesario tener en cuenta algunas variables que en definitiva no pudieron ser controladas debido a las características de nuestra población objeto.
La evaluación empleada en la segunda fase (virtual) no pudieron ser totalmente supervisadas por el profesor, debido a que los estudiantes estaban en sus casas y si bien se pidió la colaboración de los padres y se insistió a los estudiantes para que fueran muy honestos, esta es una variable que no deja de generar incertidumbre.
También es una variable para considerar, el hecho de que los estudiantes de la fase 2 (virtual) eran estudiantes que estaban cursando grado octavo, lo que significa que el año 2020 ya habían trabajado operaciones con números reales. Si bien, se les hizo antes una prueba diagnóstica y los resultados justificaban la aplicación de la herramienta m-learning, puede ser que muchos de ellos solo hayan tenido que recordar, aun así, la aplicación cumplió su objetivo.
Los conflictos epistemológicos que trae consigo el concepto de número negativo, no son un problema de investigación que esté concluido, a pesar de los grandes esfuerzos que se han realizado desde la pedagogía y la didáctica de la matemática, e inclusive los realizados en esta investigación, aun no se tiene la metodología ni las herramientas necesarias para garantizar la efectividad de este aprendizaje. Consideramos que la herramienta diseñada, desarrollada e implementada en esta investigación, es una manera efectiva para que los estudiantes logren superar tan solo uno de los seis obstáculos epistemológicos de los que Herrrera & Zapatera (2019), exponen en su artículo.
Las herramientas m-learning son alternativa que están dando resultados excelentes en el proceso de enseñanza y aprendizaje, sin embargo, en Colombia esta tecnología se ve muy limitada para los estudiantes de zonas rurales que no cuentan con dispositivos móviles ni conectividad, muchos de los esfuerzos realizados por los docentes en el diseño y desarrollo de estas herramientas quedan trucados por estas limitantes.