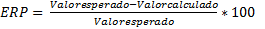Introducción
En los procesos de producción de etanol se hace necesario cuantificar las cualidades del etanol producido. Este análisis demanda procedimientos de laboratorio que imponen un tiempo entre recolecta de la muestra y la obtención de los resultados. Este tiempo afecta la velocidad de reacción del sistema de control de producción y, consecuentemente, influye en la variación de la calidad del etanol (Teixeira, 2014). De aquí la necesidad de determinar las propiedades en el menor tiempo posible, hecho que ha llevado a que en la actualidad se empleen modelos de simulación para predecirlas.
Una de las razones fundamentales por la que los simuladores de procesos son exitosos, es su habilidad para modelar con precisión el comportamiento termodinámico de las mezclas de fluidos con muy poca información de entrada por parte del usuario. La mayoría de los simuladores tienen una gran base de datos de componentes y una amplia variedad de modelos termodinámicos y correlaciones estadísticas que se incluyen en el paquete de propiedades físicas disponibles (Pérez, et al., 2010a).
Dado que la información relacionada con la estimación de propiedades de mezclas etanol-agua se encuentra dispersa en la literatura, que en todos los casos no se brinda la calidad del ajuste ni el error de estimación de las propiedades calculadas (Pérez, et al., 2010b) por medio de los modelos matemáticos convencionales, y que la relación entre las propiedades físicas y termodinámicas es altamente no lineal, es que se inicia en la actualidad el empleo de las redes neuronales artificiales (RNA), pues logran ser una alternativa adecuada para modelar y desarrollar una relación no lineal entre la entrada y los parámetros de salida.
Las RNA han demostrado ser muy exitosas para proporcionar una extracción de datos de manera precisa e interesante. Se ha encontrado una amplia aplicación en el campo de la termodinámica como la estimación de la viscosidad, la densidad, presión de vapor, factor de compresibilidad y equilibrio líquido-vapor, entre otras propiedades (Karunanithi, et al., 2014).
Existen modelos basados en algunos resultados experimentales que están pensados para predecir los datos requeridos y evitar más experimentos. Estos modelos proveen una conexión entre las variables de entrada y de salida con baja complejidad dentro del sistema. La habilidad para aprender el comportamiento de los datos generados por un sistema certifica la versatilidad de las redes neuronales (Moghadassi, et al., 2009).
Las ventajas de las RNA para la estimación de propiedades termodinámicas están dadas por modelar un proceso sin requerir suposiciones acerca de la naturaleza del mecanismo fenomenológico, aprender de las relaciones lineales y no lineales entre las variables de un grupo de ejemplos y tener alta capacidad de modelar simultáneamente múltiples salidas y una aplicación razonable del modelo para un conjunto de datos escasos (Andrade, et al., 2016).
El tipo de RNA más empleado en la predicción de propiedades es el Perceptron multicapas, el método de preferencia en el entrenamiento ha sido el “back propagation” o retroalimentación hacia atrás, usando como funciones de activación las sigmoidea e hiperbólica. El programa utilizado en la mayoría de las predicciones para el diseño, validación y empleo de las RNAs ha sido el MatLab, pues consta con una amplia opción de tipos de RNAs y métodos de entrenamiento.
En el presente trabajo, se estableció como objetivo general estimar datos de propiedades físicas tales como densidad, viscosidad dinámica y cinemática, conductividad térmica, así como datos de equilibrio como presión y fracción másica del etanol en la fase vapor a partir de valores de temperatura y fracción másica del etanol en fase líquida. Las redes se diseñaron en MatLab 2017 empleando como criterios de selección el error cuadrático medio (ECM), el coeficiente de regresión (R), así como el error relativo promedio (ERP). Se determinó la influencia de las variables independientes en la predicción de las propiedades con la RNA y se diseñó una interfaz de usuario personalizada, que unifica las dos redes neuronales antes mencionadas, la cual facilita el trabajo de predicción a partir un mismo valor de temperatura y de fracción másica de etanol en la fase líquida.
Materiales y métodos
La base de datos empleada para la realización de este trabajo se obtuvo de valores reportados en la literatura (Stabnikov, 1976; Zumalacárregu, et al., 2018). Teniendo en cuenta que es una fase crítica dentro de la minería de datos, se realizó una transformación y limpieza de los datos para conformar el conjunto a utilizar para la modelación.
Se preparó la información que será procesada por la RNA y se redujo la cantidad de información redundante. Una buena selección puede mejorar la calidad del modelo obtenido, ya que se centra solamente en las características relevantes. Permite expresar el modelo resultante en función del menor número de variables posibles. Se agruparon los datos en dos libros Excel; el primero contiene los datos de las propiedades físicas y el segundo los datos referentes al equilibrio líquido-vapor.
En el caso del Libro de Excel que contiene los datos referentes a las propiedades físicas se escogió un intervalo de temperatura que abarca valores desde 0 °C a 70 °C, mientras que para la fracción másica del etanol en la fase líquida el intervalo seleccionado abarca valores de 0 % a 100 %. En cambio, para el Libro de Excel que contiene los datos referentes al equilibrio de fases se tomó un intervalo de temperatura que abarca desde 20 °C hasta 197,40 °C y se mantuvo el mismo intervalo de valores de fracción másica del etanol en la fase líquida seleccionado para el primer libro. Esta selección responde a la recopilación de datos realizada durante el estudio de la literatura.
Para trabajar con las redes neuronales fue necesario aplicar a los datos el proceso de normalización dependiendo de la salida de los resultados que se desea obtener. Uno de los métodos más utilizados para normalizar datos es el máximo (MAX) (ecuación 1) y es el que se usó en el presente trabajo. Los datos que se quieren normalizar se encuentran dentro del vector Datos (i), con i = 1…n. El procedimiento a seguir es el siguiente (Quintana, 2015):
Se busca el máximo del vector
Se normalizan los datos según la relación:
(1)
Todos los valores se normalizaron a partir de determinar los máximos de cada variable y empleando la ecuación 1, se obtuvieron dos tablas cuyos valores estaban en un intervalo de 0 a 1.
MatLab - Redes neuronales artificiales
MatLab presenta una caja de herramientas denominada “Neural Network Toolbox”, paquete que contiene una serie de funciones para crear y trabajar con redes neuronales artificiales. Así pues, proporciona las herramientas para el diseño, la puesta en práctica, la visualización, y la simulación de redes neuronales.
Se decidió desarrollar dos redes del tipo “Perceptron multicapas” constituidas por tres capas de neuronas. La primera capa está formada por dos neuronas correspondientes a las variables independientes. La segunda, constituye la capa oculta y contiene inicialmente, para ambas redes diseñadas la misma cantidad de neuronas que de variables a predecir por la red. La última capa está formada, en el caso de la red empleada en la predicción de las propiedades físicas por cuatro neuronas mientras que la red que se diseñó para la predicción de las propiedades de equilibrio contiene dos neuronas en esta capa.
Se evaluó el comportamiento de ambas redes neuronales variando el número de neuronas de la capa oculta hasta 20. Este incremento se realizó hasta obtener parámetros que ratifiquen la calidad de predicción de la red en desarrollo. Como criterio de selección de la mejor red o topología se empleó el error cuadrático medio (ECM) y el coeficiente de correlación (R) y como criterios complementarios se empleó la prueba de Friedman, la prueba de Wilcoxon y el error relativo promedio (ERP) de estimación; se tuvo en cuenta también la información que brinda la gráfica de desempeño de entrenamiento “plotperform” de MatLab, dado que, si la curva de prueba aumenta significativamente antes del aumento de la curva de validación, es posible que haya ocurrido un sobreajuste.
Con la prueba de Friedman se comprobó si existían diferencias estadísticamente significativas entre el comportamiento (error cuadrático medio) de las topologías creadas. Si existían diferencias significativas se aplicó la prueba de Wilcoxon (López, et al., 2018), que permite la comparación entre dos topologías para determinar si existen o no diferencias significativas entre los errores cuadráticos medios.
Contribución de las variables independientes en la predicción
En la literatura existen varios métodos que posibilitan analizar de una forma explicativa los datos internos que se generan durante el desarrollo de una red. Estos métodos posibilitan a su vez determinar la importancia que tiene o no una variable de entrada en la tarea que está realizando la red; es decir la contribución de la variable.
En el caso del presente trabajo se emplea el método de los pesos de conexión para el cálculo de la importancia relativa (IR) (Oña & Garrido, 2014).
Para cada neurona de una capa oculta h, según la ecuación 2 se divide el valor absoluto del peso de la conexión de la neurona de entrada - capa oculta (Wih) por el valor absoluto de la suma de los pesos de conexión de las neuronas de entrada - capa oculta.
Para h = 1 a nh, i = 1 a ni,
(2)
Para cada neurona de la capa de entrada i (ecuación 3), se divide la suma de las Qih para cada neurona de la capa oculta por la suma para cada neurona de la capa oculta por la suma para cada neurona de la capa de entrada de Qih, multiplicado por 100.
Para i = 1 a ni
(3)
Resultados y discusión
Se diseñaron 17 redes neuronales comenzando por cuatro neuronas en la capa oculta hasta alcanzar las 20 neuronas, manteniendo un incremento de una neurona de un diseño a otro. Teniendo en cuenta que las medias de los ECM de todas las topologías tienen el mismo orden, se aplicó la prueba de Friedman para comprobar si estos valores eran significativamente diferentes, para un 95 % de confianza, concluyéndose que no existían diferencias estadísticamente significativas en el comportamiento de las diferentes topologías de acuerdo con el criterio de ECM pues el valor-P es de 0,8127 > α.
Se calculó el ERP para cada topología, tomando como criterio de selección valores de ERP lo más cercano o menores que el 5 %. Se usó la ecuación 4 la cual se programó en un Libro de Excel a partir del empleo de los valores que se obtienen durante la validación de la red (Tabla 1).
(4)
Tabla 1 - Criterios de selección.
| Topología | ECM | R | ERP (%) |
|---|---|---|---|
| 2 - 4 - 4 | 2,2703 x 10-3 | 0,9880 | 8,95 |
| 2 - 5 - 4 | 1,0908 x 10-3 | 0,9956 | 8,45 |
| 2 - 6 - 4 | 6,8966 x 10-3 | 0,9604 | 4,73 |
| 2 - 7 - 4 | 5,7748 x 10-4 | 0,9975 | 9,42 |
| 2 - 8 - 4 | 1,7969 x 10-3 | 0,9927 | 8,69 |
| 2 - 9 - 4 | 1,0607 x 10-3 | 0,9950 | 11,10 |
| 2 - 10 - 4 | 1,7662 x 10-4 | 0,9992 | 5,20 |
| 2 - 11 - 4 | 2,0927 x 10-4 | 0,9991 | 3,61 |
| 2 - 12 - 4 | 1,2080 x 10-4 | 0,9991 | 3,67 |
| 2 - 13 - 4 | 8,6810 x 10-5 | 0,9996 | 2,40 |
| 2 - 14 - 4 | 1,0773 x 10-3 | 0,9937 | 5,01 |
| 2 - 15 - 4 | 1,8308 x 10-3 | 0,9921 | 12,98 |
| 2 - 16 - 4 | 4,3233 x 10-4 | 0,9977 | 3,95 |
| 2 - 17 - 4 | 1,6915 x 10-3 | 0,9910 | 5,76 |
| 2 - 18 - 4 | 3,1555 x 10-3 | 0,9845 | 8,50 |
| 2 - 19 - 4 | 4,5550 x 10-3 | 0,9772 | 13,04 |
| 2 - 20 - 4 | 3,2849 x 10-3 | 0,9845 | 11,27 |
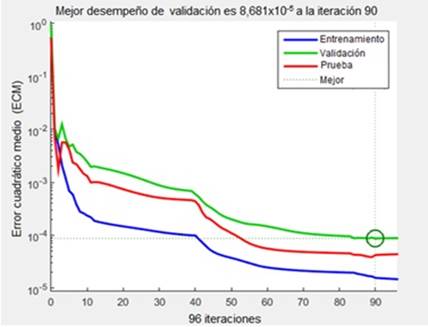
Se seleccionó como mejor red la que presenta una topología 2 - 13 - 4, ya que muestra el menor valor del ECM y de ERP, así como el mayor valor de R con respecto a las otras redes desarrolladas. Además, su gráfico de desempeño, la Fig. 1, muestra que la curva de desempeño de la prueba (roja) se mantiene por debajo de la curva de desempeño de la validación (verde), lo que significa que no ha existido posiblemente un sobre entrenamiento de la red.
Se desarrollaron 19 redes neuronales comenzando por dos neuronas en la capa oculta hasta alcanzar las 20 neuronas, manteniendo un incremento de una neurona de un diseño a otro. Después de aplicar la prueba de Friedman se concluyó que no existían diferencias estadísticamente significativas en el comportamiento de las diferentes topologías de acuerdo con el criterio de ECM, pues el valor-P es de 0,5248 < α y por tanto se acepta la hipótesis nula.
Se calculó el ERP para cada topología, los resultados obtenidos son los que se muestran en la Tabla 2.
Tabla 2 - Criterios de selección.
| Topología | ECM | R | ERP (%) |
|---|---|---|---|
| 2 - 2 - 2 | 7,1881 x 10-3 | 0,9617 | 16,76 |
| 2 - 3 - 2 | 5,9244 x 10-4 | 0,9975 | 19,58 |
| 2 - 4 - 2 | 3,9467 x 10-4 | 0,9981 | 14,09 |
| 2 - 5 - 2 | 3,6855 x 10-4 | 0,9983 | 10,62 |
| 2 - 6 - 2 | 1,4036 x 10-4 | 0,9992 | 11,73 |
| 2 - 7 - 2 | 7,9563 x 10-4 | 0,9963 | 11,78 |
| 2 - 8 - 2 | 4,4680 x 10-4 | 0,9978 | 9,07 |
| 2 - 9 - 2 | 3,5963 x 10-4 | 0,9980 | 14,32 |
| 2 - 10 - 2 | 5,1805 x 10-4 | 0,9980 | 12,78 |
| 2 - 11 - 2 | 1,4902 x 10-4 | 0,9993 | 4,04 |
| 2 - 12 - 2 | 7,0909 x 10-3 | 0,9686 | 8,33 |
| 2 - 13 - 2 | 4,5294 x 10-4 | 0,9978 | 12,76 |
| 2 - 14 - 2 | 4,3211 x 10-3 | 0,9807 | 6,77 |
| 2 - 15 - 2 | 3,9442 x 10-4 | 0,9980 | 8,58 |
| 2 - 16 - 2 | 5,5137 x 10-4 | 0,9971 | 10,56 |
| 2 - 17 - 2 | 1,1907 x 10-3 | 0,9947 | 14,80 |
| 2 - 18 - 2 | 3,1870 x 10-4 | 0,9986 | 8,73 |
| 2 - 19 - 2 | 6,9198 x 10-4 | 0,9677 | 5,13 |
| 2 - 20 - 2 | 6,7558 x 10-4 | 0,9966 | 13,93 |
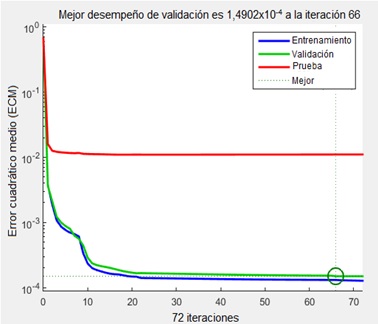
Si se realizara un ordenamiento lógico de las redes para cada uno de los parámetros de acuerdo al criterio de selección se podría decir que la red cuya topología es 2 - 11 - 2 es la de mejor trío de valores; ECM es el segundo mejor valor del grupo de redes, R el mayor valor y ERP el menor valor reportado. Pero si se observa la Fig. 2 se puede apreciar que posiblemente esta red sufrió un sobre entrenamiento, dado que la curva de desempeño de prueba supera a la curva de desempeño de la validación, por tal motivo se descarta la selección de esta red.
FSiguiendo el mismo razonamiento se descartan las redes cuyas curvas de desempeño mantienen un comportamiento similar a la anterior. Luego de depurar el grupo de redes desarrollada a partir del criterio anterior se obtiene la Tabla 3.
Tabla 3 - Redes que no mostraron un posible sobre entrenamiento
| Topología | ECM | R | ERP (%) |
|---|---|---|---|
| 2 - 2 - 2 | 7,1881 x 10-3 | 0,9617 | 16,76 |
| 2 - 3 - 2 | 5,9244 x 10-4 | 0,9975 | 19,58 |
| 2 - 7 - 2 | 7,9563 x 10-4 | 0,9963 | 11,78 |
| 2 - 12 - 2 | 7,0909 x 10-3 | 0,9686 | 8,33 |
| 2 - 14 - 2 | 4,3211 x 10-3 | 0,9807 | 6,77 |
| 2 - 19 - 2 | 6,9198 x 10-4 | 0,9677 | 5,13 |
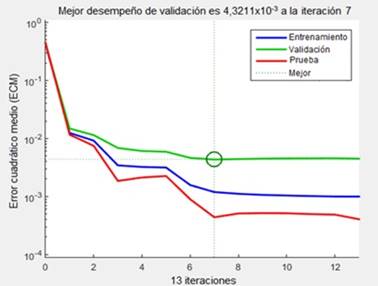
En tal sentido se seleccionó la red cuya topología corresponde a 2 - 14 - 2; presenta el cuarto menor valor de ECM, el tercer mayor valor de R, el segundo menor valor de ERP y contiene cinco neuronas menos que la red de mejor valor de ERP, hecho que asegura que no haya ocurrido el sobre entrenamiento de la red, dado que entre más neuronas tenga la capa oculta las probabilidades de sobre entrenarse son mayores; y en la Fig. 3 se observa que esta red no sufrió un sobre entrenamiento, dado que la curva de desempeño de prueba no supera a la curva de desempeño de la validación.
En la literatura (Pérez, et al., 2010a; Sánchez, 2011; Acosta, et al., 2016; Lauzurique, et al., 2016; Hernández, 2017) se encontraron modelos estadísticos de estimación de propiedades de la mezcla binaria etanol-agua. El uso de los modelos obtenidos está limitado al intervalo de temperatura y presión para el que se desarrolló cada uno.
En comparación con los 240 modelos mostrados en la Tabla 4 se puede apreciar que el modelo propuesto en este trabajo presenta una mejor capacidad de generalización, se logra eliminar las limitaciones de los intervalos de presiones y la diversidad de modelos estadísticos a emplear.
Tabla 4 - Comparación de los modelos obtenidos con los existentes en la literatura.
| Propiedades | Modelo | Cantidad | ERP (%) | R | ECM | Fuente |
|---|---|---|---|---|---|---|
| Físicas | ρ = f(T;x1) | 3 | 0,18 | 0,9998 | - | (Pérez, et al., 2010a) |
| μd = f(T;x1) | 4 | 3,57 | 0,9897 | - | ||
| k = f(T;x1) | 4 | 5,70 | 0,9950 | - | ||
| De equilibrio (6,7 a 98,7 kPa) | y1 = f(x1) | 50 | 0,32 | - | - | (Acosta, et al., 2016) |
| y1 = f(T) | 25 | 0,98 | 0,9902 | - | ||
| De equilibrio (101,3 kPa) | y1 = f(T) | 2 | - | - | - | |
| De equilibrio (203 a 811 kPa) | y1 = f(x1) | 47 | 0,01 | - | - | (Lauzurique, et al., 2016) |
| y1 = f(T) | 25 | 0,55 | 0,9938 | - | ||
| De equilibrio (912 a 1520 kPa) | y1 = f(x1) | 57 | 0,00 | - | - | (Sánchez, 2011) |
| y1 = f(T) | 22 | 0,80 | 0,9792 | - | ||
| De equilibrio (6,67 a 1519,88 kPa) | (y1;x1) = f(T;P) | 1 | - | 0,9729 | 5,40x10-3 | (Hernández, 2017) |
| Físicas | (ρ,μd,μc,k) = f(T;x1) | 1 | 2,40 | 0,9996 | 1,49x10-4 | Este trabajo |
| De equilibrio (6,67 a 1519,88 kPa) | (P;y1) = f(T;x1) | 1 | 6,77 | 0,9807 | 4,32x10-3 |
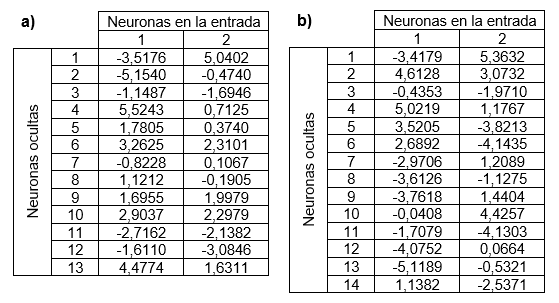
La Tabla 5 muestra los pesos de la conexión (Wih) entre las neuronas de la capa de entrada (i) y las neuronas en la capa oculta (h); se obtuvieron ejecutando el comando net.IW en el espacio de trabajo de MatLab para cada red seleccionada; el término net hace referencia al nombre de la red.
Para ambas redes la columna 1 corresponde a la variable fracción másica del etanol en la fase líquida y la columna 2 a la temperatura.
Empleando las ecuaciones 2 y 3 se obtienen los valores de la importancia relativa de las neuronas de entrada de cada red, las cuales corresponden a las variables independientes. Los valores obtenidos son los que se muestran en la Tabla 6.
Tabla 6 - Valores de IR (%).
| RNA | Neuronas a la entrada | |
|---|---|---|
| 1 | 2 | |
| 2 - 13 - 4 | 64,78 | 35,22 |
| 2 - 14 - 2 | 53,93 | 46,07 |
Como se puede apreciar para ambas redes la fracción másica del etanol en la fase líquida (columna 1) tiene mayor importancia que la temperatura (columna 2). Esto demuestra que x1 hace una mayor contribución a la predicción de las propiedades que la temperatura.
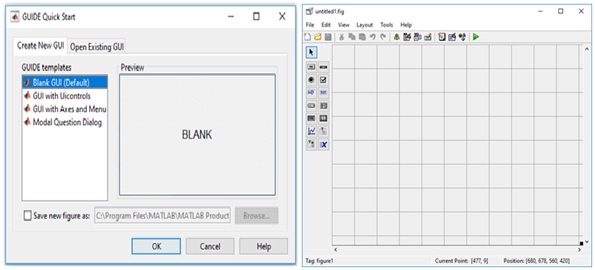
Otra de las bondades de MatLab es su paquete para el diseño, programación y empleo de la interfaz de usuario (Barragán, 2014). Tecleando en el espacio de trabajo de MatLab el comando “guide” se logra acceder a esta ventana (Fig. 4a), la cual permite crear la interfaz de usuario. Seleccionado la primera opción, se accede a otra ventana que permite diseñar el espacio de la interfaz.
Empleando la paleta de opciones que se presenta en el lado izquierdo (Fig. 4b), se puede introducir en el espacio de trabajo botones de comando (“pushbotton”), cuadro de texto (“text”) para la creación de las etiquetas, cuadros de edición (“edit”) con los que se introducen los valores y por los que se visualiza el resultado, y un fondo de interfaz (“background”). Teniendo en cuenta las variables independientes y las predichas seleccionadas se diseñó la interfaz.
Automáticamente al crear la interfaz MatLab realiza una salva identificando dos archivos: “interfa.fig” y el otro es “interfa.m”, de acuerdo a los nombres asignados por el usuario y los almacena en la dirección señalada por este. La diferencia entre estos archivos está dada por la extensión que le asigna el programa.
La extensión .m corresponde a un archivo de tipo función, característica de MatLab. Este archivo se construye automáticamente por MatLab y las líneas de código son las que crean la interfaz que aparece en el archivo interfa.fig. El archivo de inicialización define los parámetros básicos de la interfaz y crea un conjunto de “handles” para cada uno de los objetos que vayan apareciendo sobre la interfaz.
Accionando sobre cualquier objeto dentro del espacio de trabajo de la interfaz, Fig. 5, y seleccionando la opción “View Callbaks” y posteriormente “Callbaks” se accede al espacio de trabajo de MatLab que posibilita la programación de cada uno de los objetos introducidos en el diseño gráfico de la interfaz.
Comando “Predecir”
Como bien indica el nombre del botón, su objetivo es predecir las propiedades de la mezcla etanol-agua mediante el empleo de las dos redes seleccionadas.
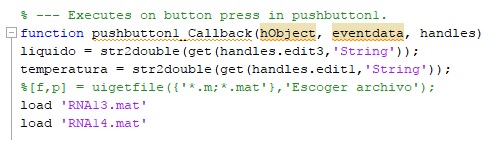
El primer paso es la creación de las variables independientes, Fig. 6. El término get se emplea para captar el texto que se escribe en los cuadros de edición, texto que se define por el uso de la palabra string; debido a que el programa no puede realizar operaciones aritméticas con texto se convierte la información en números dobles mediante la orden str2double.
Seguidamente se programa la orden para que la interfaz cargue las redes seleccionadas, las cuales deben estar ubicadas dentro de la misma carpeta de la interfaz. La orden de cargar de las redes se realiza mediante el empleo del comando load.
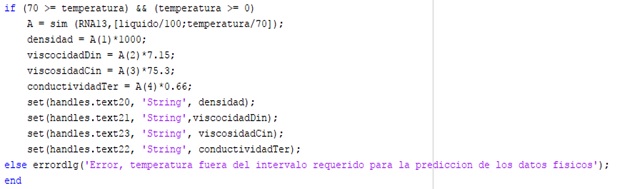
La programación para predecir las propiedades físicas, Fig. 7, se inicia con una condición empleando el comando “if”; se establecieron los límites para los cuales esta condición es efectiva. En este caso corresponden a los valores máximo y mínimos de la temperatura del sistema. Se declara la conformación de una matriz con el comando A = sim, el cual además establece la acción de llamar a la red que se especifica. Debido a que la red trabaja con datos normalizados entre valores de 0 y 1 se programa dentro de este comando la transformación de los datos que se introducen en los cuadros de edición de cada variable independiente hacia valores normalizados, líquido/100 y temperatura/70.
El resultado obtenido es una matriz de una fila y cuatro columnas. A continuación, se declaran las variables predichas y las posiciones que tendrán cada una dentro de la matriz, así como la transformación de los valores obtenidos normalizados hacia valores no normalizados: densidad = A (1) * 100, viscosidadDin = A (2) * 7,15, respectivamente. Los resultados se muestran en los respectivos cuadros de texto mediante el empleo del comando set y especificando la ubicación de cada uno: set (handles.text20, 'String', densidad).
Se programó la acción a seguir por la interfaz en el caso que no se cumpla la condición establecida. Por ejemplo, en el caso que la temperatura no se encuentre entre el intervalo señalado, tanto para las propiedades físicas como para las propiedades de equilibrio, la interfaz muestra un cuadro de error con un aviso; esto se logra mediante el empleo del comando: errordlg. Al no existir otra limitación se cierra la condición mediante el comando end.
Para predecir propiedades de equilibrio, se realizó la misma operación explicada para la predicción de propiedades físicas. Se emplearon los mismos comandos descritos anteriormente, se especificaron los límites de la temperatura para esta red y se especificaron las variables predichas, Fig. 8.
Comando “Borrar”
El objetivo de este comando es el de borrar los textos que se introducen en los cuadros de edición y en los cuadros de texto. Esta operación se logra primeramente declarando la acción de limpieza mediante la variable ini y el comando char (´ ´), seguidamente se especifican los objetos dentro de la interfaz que serán modificados con este comando (Fig. 9).
Tapiz de la interfaz
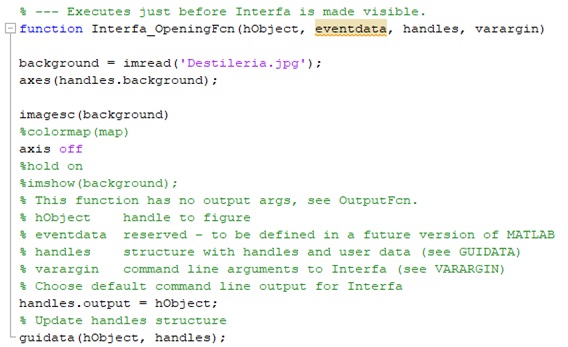
Con vista a personalizar la interfaz se programó un comando que facilita cargar y mostrar una imagen de fondo, un tapiz, en la interfaz. Esto se logra primeramente nombrando el fondo y programando la acción de cargar el fondo que se quiere mostrar. Para esto se ubicó en la carpeta del programa la imagen a mostrar y posteriormente en el archivo tipo .m en la sección correspondiente al fondo de la interfaz se declaró el fondo como background y se estableció mediante el comando imread la orden de cargar la imagen especificando el nombre de la misma.
Para mostrar dicho fondo se introdujo en la interfaz un objeto gráfico; mediante el comando axes se estableció que el fondo se mostrara en este objeto. Con el comando imagesc fue posible el cambio de escala y hacer visible la imagen. Con el empleo de la orden axes se logró que la imagen seleccionada se muestre a todo lo largo y ancho de la interfaz (Fig. 10).
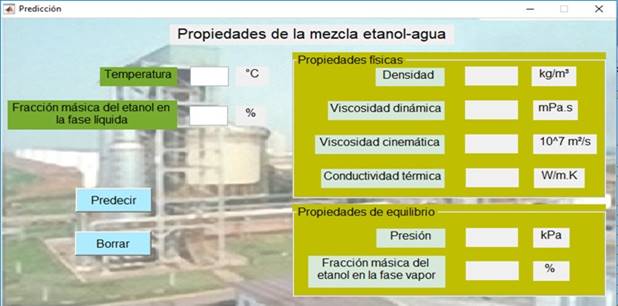
En la Fig. 11 se puede observar cómo quedó diseñada la interfaz, la cual se encuentra lista para su empleo.
Conclusiones
Se desarrollaron 36 redes neuronales; divididas en dos grupos, 17 destinadas a la predicción de las propiedades físicas y 19 a las de equilibrio.
Se seleccionaron las dos mejores redes neuronales para cada caso. La red neuronal para la predicción de las propiedades físicas fue la de topología 2-13-4 con ECM, R y ERP (8,6810 x 10-5; 0,9996 y 2,40 % respectivamente). Para el caso de la red que predice las propiedades de equilibrio se seleccionó la de topología 2-14-2 con ECM, R y ERP (4,3211 x 10-3; 0,9807 y 6,77 % respectivamente).
La fracción másica de etanol en la fase líquida tiene una mayor contribución a la predicción de las propiedades que la temperatura.
Se diseñó una interfaz de usuario personalizada, que unifica las dos redes neuronales antes mencionadas, que facilita el trabajo de predicción para un mismo valor de temperatura y de fracción másica de etanol en la fase líquida.