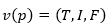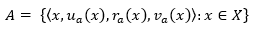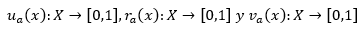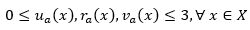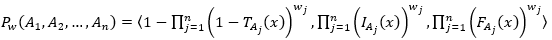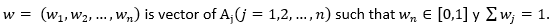Articulo original

Neutrosophical evaluation of the application of the problem-based learning in the field of differential equations

Evaluación neutrosófica de la aplicación del aprendizaje basado en problemas en el campo de las ecuaciones diferenciales

0000-0002-7323-6589Wilber Ortiz Aguilar^{1  *} 

¹ Universidad de Guayaquil. Ecuador

ABSTRACT

The present research had as objective to value the incidence of the methodology Problem Bassed Learning (PBL) as a didactic strategy in the process of teaching learning of the subject Differential Equations. For this purpose, it was based on the evaluation of two groups that received the subject during the first cycle of the 2020-2021 academic year at the University of Guayaquil. In the first group, corresponding to the Networking and Telecommunications Engineering degree, the methodology was applied in the topics of Application of differential equations of first and second order. In the second group, from the Software Engineering career, the PBL methodology was not applied. Six fundamental aspects of professional training were evaluated in engineering students, using linguistic terms associated with Single-Value Neutral Sets. The results were evidenced by the comparative analysis aspect/student, aggregated evaluation/student and in the general comparison aspect/group. In general, better results were obtained in the group in which the PBL methodology was applied with a greater impact on aspects: Communication Skills, Collaborative Work and Enhancement of Creativity.

Key words: PBL methodology; linguistic terms; single-value neutral set; aggregation oper ator; score operator

RESUMEN

La presente investigación tuvo como objetivo valorar la incidencia de la metodología Aprendizaje Basado en Problemas (ABP) como estrategia didáctica en el proceso de enseñanza aprendizaje de la asignatura Ecuaciones Diferenciales. Para ello, se basó en la evaluación de dos grupos que recibieron la asignatura durante el primer ciclo del año académico 2020-2021 en la Universidad de Guayaquil. En el primer grupo, correspondiente a la carrera de Ingeniería en Redes y Telecomunicaciones, se aplicó la metodología en los temas de Aplicación de ecuaciones diferenciales de primer y segundo orden. En el segundo grupo, de la carrera de Ingeniería de Software, no se aplicó la metodología PBL. Se evaluaron seis aspectos fundamentales de la formación profesional en estudiantes de ingeniería, utilizando términos lingüísticos asociados a Conjuntos Neutrales de Valor Único. Los resultados fueron evidenciados por el aspecto de análisis comparativo / estudiante, evaluación agregada / estudiante y en el aspecto de comparación general / grupo. En general, se obtuvieron mejores resultados en el grupo en el que se aplicó la metodología ABP con mayor impacto en los aspectos: Habilidades comunicativas, Trabajo colaborativo y Potenciación de la creatividad.

Palabras-clave: Metodología ABP; términos lingüísticos; conjunto neutro de valor único; operador de agregación; operador de partitura

Introduction

The development of problem-solving skills is one of the most important objectives of education in general, and in the teaching of Mathematics related subjects in particular. Problem solving is, therefore, widely used by science teachers both to instruct and to evaluate learning. The fact that students must be taught to solve the problems specific to each discipline should not imply that the teaching of problem solving is approached in a different or disconnected way from what happens in other disciplines. Although conceptual knowledge is specific to each domain, strategies and mental skills to solve problems do not differ significantly (^{Nurkhin, et al., 2020}; ^{Juandi & Tamur, 2021}).

The methodology of Problem-Based Learning (PBL) constitutes the bridge that joins the theoretical principles of constructivism, instructional design and teaching practice. It is a teaching/learning strategy that has been applied for more than forty years in university teaching. It attempts to shift the concept of teaching based predominantly on the teacher as the only person responsible for transferring knowledge and the students as mere passive recipients of it, towards the identification of the student as the center and responsible for his or her own learning (^{Tong, et al., 2021}).

PBL is an active learning process that works through the solution of problems related to the interaction of man and his environment. Its essence consists of identifying, describing, analyzing and solving such problems, which is achieved through the interaction of the teacher and the students. It can be used in the orientation of all or part of a subject, even in the development of a thematic unit; the application of this strategy is based on the design of an adequate problem in such a way that the student deepens certain topics before trying to solve them (^{Castaño, 2015}).

According to ^{Juandi, et al. (2021}), the use of PBL has a greater positive effect than conventional instruction in terms of developing student's mathematical problem-solving skills. Moreover, mathematics teachers and professors should choose PBL as one of the best approaches in the implementation of mathematics teaching (^{Tong, et al., 2021}).

The goals to be achieved by PBL are: that the student becomes responsible for his self-learning; diagnoses what he needs to know about a certain problem; favors scientific reasoning from the formulation of hypotheses to the systematic search for the solution of specific problems; works harmoniously with his peers through good communication and is capable of self-evaluation (^{Castaño, 2015}; ^{Nurkhin, et al., 2020}).

^{Tong et al. (2021}), points out that "problem-based learning represents an effective and flexible strategy that, based on what students do, can improve the quality of their university learning in very diverse aspects". Thus, the PBL helps the student to develop and work on diverse competences. Among them, the following stand out (^{Alzate, et al., 2013}):

• Problem solving.

• Decision making.

• Teamwork.

• Communication skills (argumentation and presentation of information).

• Development of attitudes and values: accuracy, review, tolerance.

According to ^{Navarro & Suarez (2014}), the PBL method it allows the formation of people capable of facing the continuous change of science and disciplines, allowing them to develop the necessary learning skills to adapt and be competent with the demands of today's society. With the development of this methodology, the students will be able to obtain the suitable aptitudes to carry out any type of logical work (^{Escobar, 2018}).

PBL approaches have a extended history of effectiveness in different disciplines of high education, and has been demonstrated to be one of the best tools in formation of engineers for their professions, among the variety of existing instructive methods (^{Mann, et al., 2021}).

Based on the above and the search for effective methodological strategies, that facilitate student learning and encourage self-learning and independent work in the engineering careers of the Faculty of Mathematical and Physical Sciences of the University of Guayaquil, the teachers opted for the application of the PBL in the area of Mathematics, specifically in a regular course of Differential Equations.

The course of Differential Equations was selected because it is a subject that requires the use of previous knowledge of the courses of Differential and Integral Calculus and Linear Algebra, and at the same time provides knowledge that will be useful in other courses of the engineering area, such as Electrical Circuits, Electricity and Magnetism, among others.

The present work has as objective to value the incidence of the methodology Problem-Based Learning (PBL) as a didactic strategy in the process of teaching and learning of the subject Differential Equations.

Materials and methods

In order to meet the objective, set, the group of the Networking and Telecommunications Engineering degree course that received the subject during the first cycle of the 2020-2021 academic year (total population of 40 students, Group 1) was evaluated, in which the PBL method was applied in the topics of Application of differential equations of first and second order, respectively. As a control group, it was also evaluated the group that received the same subject, in the same period, but of the Software Engineering career, conformed by 36 students (Group 2). In this group, the PBL methodology was not applied, but the subjects of the course were taught in the traditional way.

At the end of the cycle, each student was evaluated qualitatively by the professor, between Excellent and Very Bad, in terms of the following aspects:

1. Communication skills (argumentation and presentation of information).

2. Academic Results.

3. Self-management of knowledge.

4. Collaborative work.

5. Enhancing Creativity.

6. Development of professional skills and competences.

For a more effective management of subjectivity and indetermination in the evaluations, linguistic terms associated with sets of neutral numbers were used. Below, some basic concepts of neurosophy are presented and applied in this research.

Neutrosophy is a mathematical theory developed by Florentin Smarandache to deal with indetermination (Smarandache, 1998, cited by ^{Stanujkic, et al., 2018}). It has been the base for the development of new methods to handle indeterminate and inconsistent information as the neutrosophical sets and the neutrosophical logic and, especially, in the problems of decision making (^{Smarandache, 2005}; ^{Leyva & Smarandache, 2018}; ^{Liu, et al., 2018}). The truth value in the neutrosophical set is the following (^{Gayen, et al., 2020}):

Let be 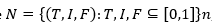, a neutral evaluation of a mapping of a group of formulas propositional to N, and for each sentence p you have:

(1)

In order to facilitate the practical application to decision-making problems, the use of Single-Value Neutral Sets (SVNS) (^{Liu & Tang, 2016}; ^{Liu & Shi, 2017}) was proposed, through which it is possible to use linguistic terms, in order to obtain a greater interpretability of the results.

Let X be a universe of discourse, a SVNS A over X has the following form:

(2)

Where

with

The intervals 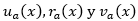denote the memberships to true, indeterminate and false from x in A, respectively. For convenience a Single Value Neutrosophic Number (SVNS) will be expressed as A = (a, b, c), where a, b, c ∈ [0.1] and satisfies 0 ≤ a + b + c ≤ 3.

The single-value weighted neutrosophical mean (SVNWA) is defined as follows (^{Leyva & Smarandache, 2018}; ^{Liu & Teng, 2018}):

Let 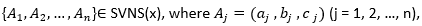then, the Single Valued Neutrosophic Weighted Average Operator is defined by:

(3)

Where:

Let A = (a, b, c) be a single neutrosophic number, a score function S of a single valued neutrosophic value, based on the truth-membership degree, indeterminacy-membership degree and falsity membership degree is defined by ^{Leyva & Smarandache, (2018}):

The evaluations of each aspect for each student were determined by the associated linguistic terms SVN numbers as shown in Table 1.

Table 1 - Linguistic terms used for the evaluation. 

Linguistic term	Evaluation	SVN Numbers
Excellent	E	(1; 0; 0)
Very Good	VG	(0,8; 0,15; 0,20)
Good	G	(0,60; 0,35; 0,40)
Regular	R	(0,50; 0,50; 0,50)
Regular Tending To Bad	RB	(0,40; 0,65; 0,60)
Bad	B	(0,20; 0,85; 0,80)
Very Bad	VB	(0; 1; 1)

To aggregate the evaluations of each student and of each aspect for the evaluation of the group as a whole, the single-value weighted neutral mean (SVNWA) calculated by equation (3) was used. The same weight was assumed for all aspects evaluated (wj equal to 0.1667).

Once the aggregations were obtained, the scoring function (4) was used to obtain a single evaluation value per student and per aspect evaluated. With this value, a qualitative evaluation was obtained by determining the belonging of the score value to one of the intervals shown in table 2. To calculate these intervals, 3 (the maximum score to be obtained) was divided by 7 (number of language terms used).

Table 2 - Intervals for student evaluation according to score function value. 

Scoring Intervals	Evaluation	Linguistic Term
[2,571 - 3]	E	Excellent
[2,143 - 2,571)	VG	Very Good
[1,714 - 2,143)	G	Good
[1,286 - 1,714)	R	Regular
[0,857 - 1,286)	RB	Regular Tending To Bad
[0,429 - 0,857)	B	Bad
[0 - 0,429)	VB	Very Bad

Based on these results, the results of the student evaluations were analyzed by group in each aspect and in general to evaluate the incidence of the application of the PBL methodology in the process of teaching and learning of the subject.

Results and discussion

The overall results of student assessment in each aspect are shown in Figures 1 and 2. The histograms presented shown the absolute frequencies observed at the end of the evaluation process, according to the linguistic terms presented in Table 2.

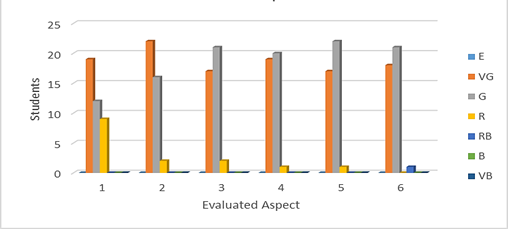Note: Group 1, in which the PBL methodology was applied

Fig. 1 - Evaluation results of students of group 1 in each aspect. 

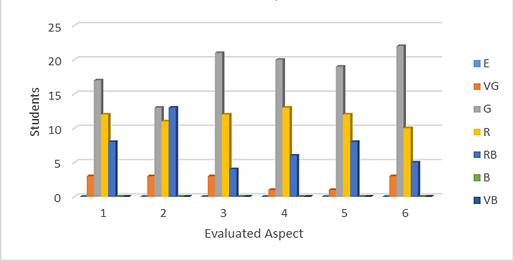Note: Group 2, in which PBL methodology was not applied

Fig. 2 - Evaluation results of students of group 2 in each aspect. 

It could be observed that in Group 1, where the PBL methodology was applied, the evaluations oscillated mostly between Good and Very Good, being greater the dispersion in the aspects of Communication skills (argumentation and presentation of information) (1) and Academic Performance (2) when reaching 19 and 22 students evaluations of Very Good and 9 and 2 evaluations of Regular, respectively. In the remaining four aspects the evaluations were between Good and Very Good, with predominance of the first, with only one student with a lower evaluation. In aspect 6 (Development of professional skills and competences) only one student was evaluated from Regular tending to Bad.

In the control group, Group 2, where the methodology was not applied, the students' evaluations were more dispersed, between Regular tending to Bad and Good, being evaluated from Very Good only between 1 and 3 students in each aspect. Although the most frequent evaluation was of Good, the evaluations of Regular and Regular tending to Bad reach important values being in some cases higher than half of the total group. In the aspect of Academic Performance (2) the worst results were observed.

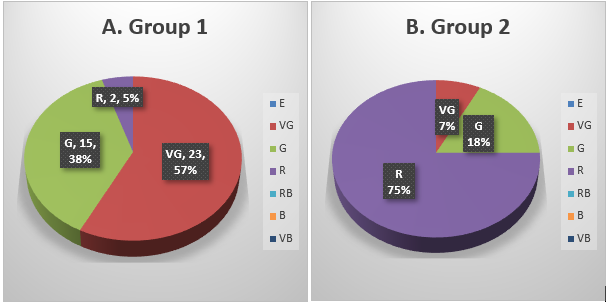
By adding the evaluations per student from the SVNWA operator, to determine their corresponding score and general evaluation, the overall results of the evaluation of the students by each group can be seen in figure 3.

Fig. 3 - Global evaluations of students in each group. 

In the first group, of the 40 students, 23 were evaluated as Very good, 15 as Good and 2 as Regular, thus showing a predominance of students with favorable evaluation. In group 2, the majority of the students were evaluated as Regular.

Adding the students' evaluations for each aspect evaluated in both groups, the results shown in table 3 were obtained.

Table 3 - General evaluation of each group by aspect evaluated. 

Evaluated Aspect	Group 1			Group 2
	Aggregated SVNS	Score	Evaluation	Aggregated SVNS	Score	Evaluation
1. Communication skills (argumentation and presentation of information)	(0,7; 0,25; 0,3)	2,141	G	(0,54; 0,44; 0,43)	1,662	R
2. Academic results	(0,72; 0,22; 0,28)	2,223	VG	(0,56; 0,41; 0,42)	1,721	G
3. Self-management of knowledge	(0,7; 0,25; 0,3)	2,148	VG	(0,58; 0,39; 0,42)	1,773	G
4. Collaborative work	(0,71; 0,24; 0,29)	2,185	VG	(0,55; 0,42; 0,44)	1,691	R
5. Enhancing Creativity	(0,7; 0,25; 0,3)	2,154	VG	(0,54; 0,43; 0,44)	1,672	R
6. Development of professional skills and competences	(0,7; 0,24; 0,29)	2,166	VG	(0,58; 0,39; 0,41)	1,776	G

In all aspects evaluated, group 1 (to which the PBL methodology was applied) obtained higher evaluations than group 2. The most significant differences were found in the aspects of Communication skills, Collaborative work and Empowerment of creativity, being remarkable the incidence of this methodology in these aspects.

The study carried out allowed verifying that the students saw their results favored in each of the aspects evaluated from the application of the PBL method. Communication skills, in terms of argumentation and presentation of information, as well as Collaborative work, were positively affected thanks to the didactic advantages offered by the method through teamwork. These results coincide with those obtained by ^{Sugiharto, et al. (2019}), and were possible due to the correct methodological use of PBL.

In these aspects, the role of the teacher as a facilitator of the debate from the use of key questions and the constant invitation to the exchange of ideas inside and outside the formed teams played a determining role. And it generated a group identification on the part of the students based on the associations among peers for the achievement of common objectives.

Derived from this same process of discussion and questioning in pursuit of debate, it was possible to achieve greater creativity when facing the solution of problems, in combination with self-management of knowledge, stimulated through the oriented extra-class activities. This allowed the development of reflections with different degrees of complexity, contributing to the improvement of learning systems, through the incorporation and critical analysis of new information. Similar results were obtained by ^{Nurdyansyah, et al. (2021}), who worked in a context of greater complexity, due to the handling of scientific and religious components in Islamic elementary schools.

These aspects described lead to the acquisition of conventional skills to face diverse learning circumstances in the future professional performance of the Networking and Telecommunications Engineering student, when faced with collective decision-making scenarios for the solution of problems typical of the work environment.

As a consequence of all the above, a higher academic performance was observed in the students of the first group, since the application of the PBL method contributed significantly to the appropriation and systematization of shared knowledge. Hence, globally, the students in Group 1 achieved a higher score in each of the aspects. By averaging the scores in Table 3, an overall difference of more than 20% can be perceived, with respect to the group in which conventional teaching methods were used.

Conclusions

Through the study of the theory consulted, it was possible to confirm that the methodology of problem-based learning (PBL) is a tool that places the student at the center of the teaching-learning process and contributes to the formation of professionals capable of adapting to the current social challenges and scientific-technical development.

The neutral evaluation of the impact of the implementation of the PBL methodology for the learning of the Differential Equations content, revealed a positive impact of this strategy, according to six fundamental aspects of the formation of the professional in students of engineering careers.

The main results were evidenced by the comparative analysis aspect/student, aggregated evaluation/student and in the general comparison aspect/group. In the latter, a greater impact on the aspects should be highlighted: Communication Skills, Collaborative Work and Empowerment of Creativity.

References

Alzate Rodríguez, E. J., Montes Ocampo, J. W., & Escobar Escobar, R. M. (2013). Diseño de actividades mediante la metodología ABP para la Enseñanza de la Matemática. Scientia et Technica, 18 (3), 542-547.

Castaño, V. (2015). El método del aprendizaje basado en problemas como una herramienta para la enseñanza de las matemáticas. Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 6(11).

Escobar Tellez, O. Y. (2018). Método ABP y su incidencia en el pensamiento analítico en matemáticas. (Tesis de grado). Campus Central Guatemala de la Asunción.

Gayen, S., Smarandache, F., Jha, S., Singh, M. K., Broumi, S., & Kumar, R. (2020). Soft Subring Theory Under Interval-valued Neutrosophic Environment. Neutrosophic Sets and Systems. An International Journal in Information Science and Engineering, 36(2020), 193-219.

Juandi, D., & Tamur, M. (2021). The impact of problem-based learning toward enhancing mathematical thinking: A meta-analysis study. Journal of Engineering Science and Technology, 16(4), 3548-3561.

Juandi, D., Kusumah, Y. S., Tamur, M., Perbowo, K. S., & Wijaya, T. T. (2021). A meta-analysis of Geogebra software decade of assisted mathematics learning: what to learn and where to go?. Heliyon, 7(5).

Leyva, M., & Smarandache, F. (2018). Neutrosofía: Nuevos avances en el tratamiento de la incertidumbre. Pons.

Liu, P. & Teng, F. (2018). Multiple attribute decision making method based on normal neutrosophic generalized weighted power averaging operator. International Journal of Machine Learning and Cybernetics, 9, 281-293.

Liu, P., & Shi, L. (2017). Some neutrosophic uncertain linguistic number Heronian mean operators and their application to multi-attribute group decision making. Neural Computing and Applications, 28, 1079-1093.

Liu, P., & Tang, G. (2016). Multi-criteria group decision-making based on interval neutrosophic uncertain linguistic variables and Choquet integral. Cognitive Computation, 8, 1036-1056.

Liu, P., Liu, J., & Merigó, J. M. (2018). Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Applied Soft Computing, 62, 395-422.

Mann, L., Chang, R., Chandrasekaran, S., Coddington, A., Daniel, S., Cook, E., & Smith, T. D. (2021). From problem-based learning to practice-based education: A framework for shaping future engineers. European Journal of Engineering Education, 46(1), 27-47.

Navarro, M. E., & Suarez, J. A. (2014). El ABP como Propuesta Pedagógica para el Desarrollo del Aprendizaje Autónomo de los Estudiantes de la Fundación Universitaria San Martín - FUSM Modalidad a Distancia. Línea de investigación Pedagogía y Didácticas, 3 (1), 98-111.

Nurdyansyah, K. S. M. T., Fahyuni, E. F., Rudyanto, H. E., & Daud, N. (2021). A new model oriented on the values of science, islamic, and problem-solving in elementary schools. Psychology and Education Journal, 58(2), 2668-2679.

Nurkhin, A., Kardoyo, K., Pramusinto, H., Setiyani, R., & Widhiastuti, R. (2020). Applying Blended Problem-Based Learning to Accounting Studies in Higher Education; Optimizing the Utilization of Social Media for Learning. International Journal of Emerging Technologies in Learning (iJET), 15(8), 22-39.

Smarandache, F. (2005) A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability: Neutrsophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability. Infinite Study, 1-141.

Stanujkic, D., Smarandache, F., Zavadskas, E. K., & Karabasevic, D. (2018). An Approach to Measuring the Website Quality Based on Neutrosophic Sets. Infinite Study .

Sugiharto, B., Corebima, A. D., & Susilo, H. (2019). The Pre-Service Biology Teacher Readiness in Blended Collaborative Problem Based Learning (BCPBL). International Journal of Instruction, 12(4), 113-130.

Tong, D. H., Uyen, B. P., & Le Thi Quynh Nhu, L. K. (2021). Application Of Problem-Based Learning To Teaching The Relationships Within A Triangle And Solution Of Triangles. International Journal of Multicultural Education, 7(7).

Received: October 20, 2021; Accepted: December 12, 2021

^*Autor para correspondencia. E-mail: [e-mail]

Los autores declaran que esta investigación no presenta conflicto de intereses.

Los autores participaron en la redacción del trabajo y análisis de los documentos.