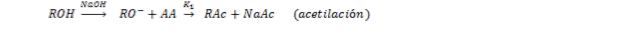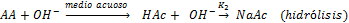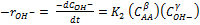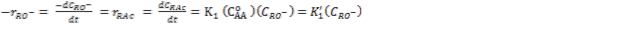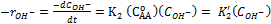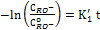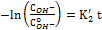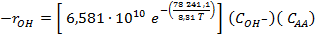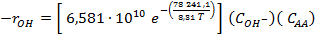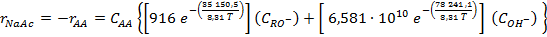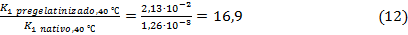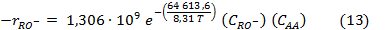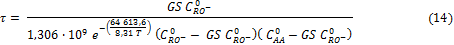Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Desde finales del siglo pasado se ha logrado un avance importante en la modelación matemática y la interpretación fenomenológica asociada a la investigación en el campo de la ingeniería química. Sin embargo, es significativo que todavía muchos de los trabajos reportados, incluso al máximo nivel, tratan a los reactores químicos y biológicos dentro de una etapa, sin considerar sus interioridades como fenómeno. Es evidente que la modelación de reactores, donde se producen simultáneamente fenómenos de transferencia de masa y de calor, junto con reacciones químicas, exige tener presentes muchos factores y decidir cuáles son los de mayor impacto. Algunas decisiones facilitan que se simplifiquen los modelos, pero en muchos casos, no es posible lograr reducciones importantes en su complejidad matemática (González, et al., 2020).
Por otra parte, para el diseño y evaluación de reactores es necesaria la modelación previa de la cinética, sea puramente química o asociada a procesos difusionales y la evolución de la transferencia de calor según la forma de operación (Smith, 1991). De acuerdo a lo anterior y teniendo en cuenta que la industria química cubana actual demanda la reducción de importaciones, el incremento del valor agregado de sus productos y el logro de altas eficiencias materiales y energéticas, es vital la contribución de la ingeniería de las reacciones químicas como disciplina científica al desarrollo de nuevos procesos del sector.
En los últimos años, se han logrado avances importantes en la modelación matemática de varios procesos de la industria química cubana que han contribuido de forma decisiva a la independencia tecnológica y la asimilación efectiva de tecnologías existentes en las condiciones exigidas por los nuevos procesos inversionistas y la reconversión industrial. En ese caso se encuentra un grupo de importantes resultados científicos presentados por González, et al. (2019), entre los cuales destaca el desarrollo de los procesos de producción de almidón nativo y modificado a partir de yuca, la producción de biomasa proteica utilizando sustratos de la industria azucarera, la obtención de etanol mediante sacarificación y fermentación simultánea de bagazo, la hidrólisis enzimática de bagazo pretratrado, el desarrollo de procesos para la producción de acido fosfórico, el uso de micro algas del género chlorella sp. empleado vinazas cubanas como medio de cultivo y la modelación cinética del añejamiento de bebidas espirituosas.
En cada uno de los trabajos anteriores se ha puesto de manifiesto la complejidad que se presenta para obtener modelos fenomenológicos, estadísticos y combinados que describan de forma adecuada el comportamiento del reactor como equipo principal. También en los referidos caso y en otras situaciones típicas de la ingeniería química resulta evidente el nexo entre los procesos cinéticos, difusionales y de transferencia de calor y la forma de contacto entre las fases presentes, situación particularmente compleja en los procesos heterogéneos, bien sea por la presencia de varias fases o por la presencia de diferentes comportamientos reológicos del material en proceso.
Uno de los cultivos de mayor potencialidad de desarrollo en las condiciones climáticas de Cuba es Manihot esculenta Cranz (Yuca). Ello, unido a las múltiples posibilidades de aplicación del almidón acetilado como facilitador de suspensiones acuosas, estabilizante y espesante en la industria alimentaria y química en general, genera una oportunidad para la producción de almidón acetilado a partir de yuca. Esta línea de investigación se ha trabajado por un colectivo de investigadores de la Universidad Central “Marta Abreu” de las Villas en años recientes. Para ello, se ha considerado el desarrollo de los procesos de acetilación combinados con gelatinización previa y secado por aspersión y la asimilación de las tecnologías existentes para el almidón nativo de dicha fuente (Pérez, et al., 2021).
Atendiendo a los aspectos anteriores, el objetivo del trabajo es contribuir metodológicamente a la modelación matemática de reactores químicos y biológicos facilitando el desarrollo de procesos de la industria química y su aplicación como caso de estudio a la modelación del reactor de acetilación para almidón nativo y pregelatinizado de Manihot esculenta Crantz.
Para efectuar la modelación de un reactor es necesario lograr el mayor conocimiento de la siguiente información (Pérez, et al., 2020):
Propiedades termodinámicas, físicas y químicas del sistema reaccionante.
Cinética y distribución de producto de las reacciones participantes.
Características térmicas del sistema.
Características específicas y generales del catalizador para las reacciones catalizadas heterogéneas.
En la medida en que se tenga más dominio de esta información son más precisos los modelos a evaluar. Si se tiene completa información sobre los aspectos anteriores, se pueden obtener modelos muy robustos que permiten analizar la influencia de cada variable en el funcionamiento del reactor. Con dichos modelos, es posible determinar las anomalías originadas por cambios en la alimentación o alteraciones en las condiciones de operación de otros equipos que inciden sobre la operación del reactor y simular, optimizar y controlar los parámetros de operación del equipo sobre la base de un criterio técnico y económico. Si solo se conocen parcialmente los aspectos anteriores, los modelos tendrán limitaciones en su comprobación y uso, de cuya extensión depende la efectividad del análisis del proceso.
Los modelos matemáticos que representan el comportamiento de un reactor químico son agrupados de la forma siguiente (Perry & Green, 1984; Montgomery, 2004):
Modelos fenomenológicos, basados en los fenómenos físicos y químicos, expresados a través de la termodinámica, la cinética y los balances de masa y energía.
Modelos basados en correlaciones experimentales entre las variables, que se deducen y comprueban aplicando procedimientos estadísticos.
En los modelos correspondientes al primer grupo destacan los cinéticos. En ellos, la velocidad depende de múltiples factores. Se consideran de mayor impacto las concentraciones y la temperatura. Sin embargo, dependiendo del proceso, es común que sea necesario considerar la influencia del pH, los procesos difusionales presentes, la transferencia de calor y otros. De especial interés es la distribución de productos en procesos de reacciones múltiples. Por estas razones en muchas ocasiones se prefieren usar modelos asociados al segundo grupo. El estudio de la hidrólisis del bagazo con ácido sulfúrico concentrado para la obtención de etanol, reportado por Boutros Sarrouh, et al. (2005), ilustran con efectividad esta situación, donde los modelos estadísticos son usados para establecer adecuadamente los parámetros de trabajo del reactor, sin llegar a la evaluación fenomenológica.
Sin embargo, es muy común la combinación de ambos métodos pues los efectos micro cinéticos son específicos de la naturaleza del sistema y los modelos combinados pueden adaptarse con precisión al tratamiento de datos prácticos, adquiridos a través de diseños experimentales efectivos.
En sistemas homogéneos la cinética es expresada a través de la etapa química, siendo el volumen del sistema el factor determinante en el diseño y en la evaluación operacional. Sin embargo, en sistemas heterogéneos la etapa química se combina con las difusionales, siendo necesario considerar la influencia relativa de todos los procesos presentes y adquiriendo un significado determinante la búsqueda de la etapa controlante. De dicha etapa depende la definición del modelo de contacto, ponderando un factor de capacidad basado en requerimientos de volumen del equipo o de área de contacto, dependiendo del predominio de las etapas químicas o las difusionales.
Los balances de materiales y energía dependen del modelo de contacto requerido en el equipo. Para reactores continuos con agitación (RCCA) en los que, puede considerarse estado estacionario y mezclado perfecto o con escasas desviaciones del mismo, los balances son ecuaciones ordinarias. Sin embargo, para equipos discontinuos, que por sus características operacionales funcionan en estado no estacionario, los balances son ecuaciones diferenciales totales respecto al tiempo de reacción.
Situación parecida se presenta para reactores tubulares continuos con modelo de flujo en pistón (RCFP) o de escasa dispersión, que operan en estado estacionario, debido al cambio de las propiedades con la posición. En este último caso los modelos de los balances son ecuaciones diferenciales totales respecto a la posición. En ellos la posición puede ser expresada como la concentración o la conversión.
Para la combinación de modelos fenomenológicos y métodos estadísticos es conveniente orientar la modelación hacia uno de los procedimientos siguientes (Smith, 1991; Pérez, et al., 2020):
Modelo homogéneo (ideal) para reactores isotérmicos y adiabáticos:
Modelo pseudo-homogéneo con dispersión en una coordenada para operación adiabática y no isotérmica-no adiabática.
Modelo pseudo-homogéneo con dispersión de dos dimensiones para operación adiabática y no isotérmica-no adiabática (método semi-riguroso)
En este caso no se considera la variación de la difusividad efectiva de masa y la conductividad térmica con la temperatura. Se considera variación del resto de las propiedades en la dirección axial y radial. Es muy importante elegir adecuadamente las condiciones de contorno para la solución del sistema de ecuaciones diferenciales parciales. Generalmente se considera que, en las secciones de entrada y salida del reactor, los gradientes son cero.
Modelo heterogéneo bidimensional (método riguroso)
Este modelo recoge todas las diferencias posibles entre la fase sólida y el fluido reaccionante, sobre todo las diferencias de temperatura. En muchos casos la fase sólida es el catalizador presente en la reacción. Para lograr una solución adecuada del sistema de ecuaciones diferenciales se necesita la más amplia información sobre el sistema reaccionante. Su solución se obtiene aplicando métodos numéricos.
El planteamiento del modelo estadístico depende de las variables a considerar, de sus relaciones e interacciones y de las posibilidades reales de obtener datos experimentales que permitan explorar adecuadamente las variables en los rangos de trabajo. En este tipo de modelación es determinante el conocimiento o experiencia previa que se tenga del caso de estudio.
Los diseños de experimentos factoriales, completos o fraccionados, permiten evaluar modelos estadísticos considerando interacciones de primer y segundo orden. Es muy baja la probabilidad de que las interacciones de tercer orden sean significativamente importantes (Montgomery, 2004). Para la selección y evaluación del modelo se usa la regresión lineal o múltiple, se evalúan los coeficientes con datos operacionales e históricos o datos de experimentos planeados al efecto y se realiza el análisis de varianza para discriminar los términos del modelo que no tienen influencia significativa sobre la respuesta. Los diseños factoriales fraccionados y otros diseños más robustos, como el Plackett-Burman, permiten disminuir el número de corridas experimentales necesarias (González, et al., 2020).
Cuando existen relaciones no lineales entre las variables se pueden proponer modelos que contienen términos no lineales en los que se plantean exponentes que son evaluados junto a los coeficientes. En esos casos, se linealizan los términos de los modelos y se evalúan los mismos por el método de regresión no lineal múltiple (González, et al., 2020).
Para la obtención y verificación de la expresión cinética y dependiendo del modelo de contacto seleccionado para las experiencias cinéticas, es conveniente usar el método de análisis integral o el diferencial. Para las reacciones homogéneas es conveniente efectuar experiencias cinéticas en equipos discontinuos, sin embargo para procesos catalíticos heterogéneos se necesitan reactores integrales o diferenciales (Smith, 1991; Levenspiel, 1999).
El conocimiento de la cinética de las reacciones generalmente presenta un alto grado de complejidad, en lo relativo a recursos materiales y técnicas analíticas, por lo que frecuentemente se plantean simplificaciones que facilitan el análisis cinético. Entre ellas se encuentra la búsqueda del semiperíodo de reacción y el trabajo en exceso de un reactante (Scott Fogler, 2001).
En el caso de las reacciones complejas se requiere un análisis de los posibles mecanismos de reacción y el diseño experimental y analítico detallado que permita alcanzar dicho propósito. Es necesario establecer el análisis de distribución de producto, las condiciones de operación y el modelo de contacto adecuado para lograr dicha distribución (Pérez, et al., 2018b).
La simulación del comportamiento de modelos teóricos previamente desarrollados y la obtención de sus parámetros para describir el comportamiento experimental es una vía interesante de modelación cinética que se ha usado con frecuencia en biorreactores. Para ello se ajusta la diferencia entre los modelos, teórico y experimental, a través del método de los mínimos cuadrados, pruebas de hipótesis de significación del modelo o la mínima integral del error de la sumatoria de las diferencias entre ellos. Esta opción se ha usado con efectividad en la modelación de la cinética de obtención de biomasa proteica (Pérez, et al., 2019) y en la obtención de un modelo cinético pseudo-homogéneo de Michaelis-Menten para la producción de azúcares reductores totales en la hidrólisis enzimática del bagazo pretratado (González, et al., 2019).
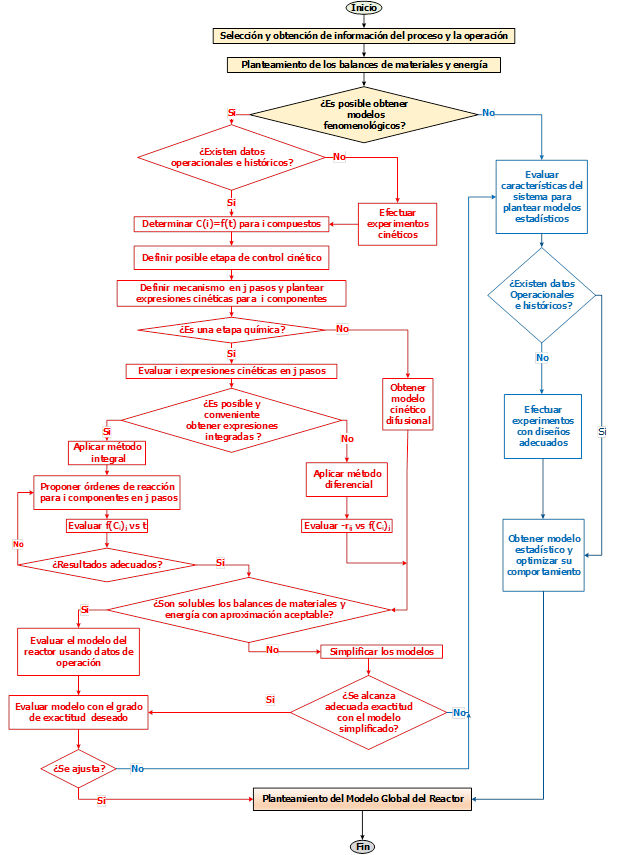
Atendiendo a los aspectos anteriores, se propuso el diagrama metodológico-heurístico para la modelación de un reactor químico o biológico mostrado en la Figura 1. El procedimiento metodológico-heurístico de la Figura 1 modifica y mejora una propuesta anterior (Pérez, et al., 2020), al desarrollar las especificaciones metodológicas necesarias para la modelación cinética y considerar diferentes vías de búsqueda de la información experimental o histórica. Dicho procedimiento, es aplicable a cualquier situación específica considerando un sistema heterogéneo pero puede aplicarse a un sistema homogéneo. En el mismo, se consideran las particularidades del sistema y se evalúa con precisión su modelo siguiendo un enfoque lógico y secuencial. En la Figura 1, las líneas Y letras rojas corresponden a las acciones de modelación fenomenológica y las líneas y letras azules al método estadístico, sin embargo resulta evidente que la opción fenomenológica se combina con procedimientos estadísticos para el diseño de experimentos y tratamiento de los resultados.
Siguiendo el diagrama de la Figura 1, luego de disponer de la información del proceso y la operación, dada por las condiciones del contacto, las posibles expresiones de caracterización y el carácter térmico de los procesos presentes, se plantean los balances de materiales y energía y dentro de ellos, las expresiones cinéticas. Posteriormente se define si es posible su solución a través de modelos fenomenológicos. En caso afirmativo, se efectúa la modelación cinética a partir de modelos de tipo fenomenológico, determinando las relaciones concentración vs tiempo de reacción para los (i) componentes involucrados, directamente desde datos operacionales e históricos, si existe esa posibilidad o efectuando experimentos diseñados con fines cinéticos.
Para la modelación cinética y considerando un sistema heterogéneo (caso más general), con proceso controlante en una etapa química, se define un mecanismo cinético probable con (j) pasos, como etapa controlante. Posteriormente se plantean las expresiones cinéticas para el mecanismo propuesto. Si el mecanismo propuesto corresponde a una etapa química, se evalúan las (i) expresiones cinéticas que responden a dicho mecanismo y sus coeficientes cinéticos. Si es posible y conveniente obtener expresiones integradas de las ecuaciones cinéticas, se aplica el método integral de análisis de datos. Para ello, se proponen los órdenes de reacción para las (i) sustancias involucradas en los (j) pasos del mecanismo, se integra la expresión cinética y se evalúa la función de la concentración para cada componente (i) en cada uno de los (j) pasos del mecanismo propuesto. Los resultados de aplicación del método integral son adecuados si se verifica linealidad en dicha función vs tiempo de reacción para los (i) componentes en los (j) pasos. Si no existe linealidad se proponen nuevos órdenes de reacción para las (i) sustancias involucradas en los (j) pasos del mecanismo.
Si no es posible y conveniente obtener expresiones integradas se aplica el método diferencial de análisis de datos. Para ello, se determinan las velocidades instantáneas de reacción para (i) componentes en (j) pasos como función de la concentración de los (i) componentes en los (j) pasos del mecanismo de reacción. Con dicha relación, a través de análisis de regresión, se determina el modelo cinético, incluidos los órdenes de reacción y coeficientes cinéticos para (i) componentes en (j) pasos.
Posteriormente, si los resultados de la aplicación del método integral son adecuados o si se aplicó el método diferencial, se verifica la exactitud lograda en la solución de los balances de materiales y energía en las condiciones cinéticas, de proceso y de frontera existentes con una aproximación aceptable. Si ello es posible, se evalúa y comprueba el ajuste del modelo a datos históricos de operación o a referencias experimentales. De lograr ajuste se plantea el modelo como expresión global del reactor con lo cual concluye el procedimiento. Cuando el mecanismo cinético propuesto no corresponde a una etapa química, se obtiene el modelo cinético difusional del proceso y también se verifica la exactitud en la evaluación de los modelos de los balances de materiales y energía.
Si la aproximación alcanzada en la solución de los balances de materiales y energía no es aceptable, se efectúan simplificaciones y se evalúa el modelo simplificado. Si el modelo simplificado no es adecuado o si el ajuste del modelo fenomenológico a los datos de operación no alcanza la exactitud necesaria, se abandona la vía fenomenológica y se procede al análisis para evaluar modelos estadísticos. Esta última opción también es considerada cuando no es posible el planteamiento de modelos fenomenológicos.
Al evaluar si las características del sistema permiten aplicar modelos estadísticos puede existir la posibilidad de contar con datos operacionales e históricos. En ese caso se obtiene el modelo estadístico y se aplica el método de optimización más adecuado al caso. En caso de no contar con datos operacionales se históricos se efectúan experimentos con diseños adecuados que permitan evaluar el modelo estadístico del equipo. El modelo estadístico en sus condiciones óptimas constituye el modelo global del reactor y con ello concluye el procedimiento metodológico.
A pesar de la integralidad del análisis anteriormente presentado, la fenomenología de un proceso de esta naturaleza es muy compleja y cada caso presenta especificidades muy marcadas. La metodología mostrada en la Figura 1 no brinda tratamiento explícito a aspectos como la distribución de productos en reacciones múltiples o el tipo de procedimiento de modelación a utilizar. Sin embargo, en ella se recogen acciones o pasos globales que deben considerar esos aspectos. Por ejemplo, la evaluación del modelo usando datos de operación para reacciones múltiples permite establecer la mejor distribución de productos y la aplicación de los métodos de análisis integral o diferencial partiendo de un planteamiento previo de los balances de materiales y energía supone la consideración de un método simplificado, semi riguroso o riguroso.
De acuerdo con lo anterior, la aplicación de la guía metodológica aquí presentada es dinámica y requiere el conocimiento detallado del proceso y la experiencia del investigador para la propuesta de un modelo ajustado a las características del proceso. Para ilustrar esa situación, a continuación se presenta un caso típico donde se obtiene el modelo operacional de un reactor para la acetilación de almidones nativo y pregelatinizado cuya fuente de obtención es yuca de la variedad INIVIT Y-93-4.
Caso: Modelación de reactor de acetilación para almidón nativo y pregelatinizado de Manihot esculenta Crantz (Yuca)
Los almidones acetilados se obtienen por sustitución de grupos hidroxilo por acetilo y tienen un comportamiento hidrofóbico que los hace atractivos como aditivos alimentarios y como facilitadores de suspensiones acuosas de la industria química y farmacéutica. Una fuente natural de almidón muy adaptable a las condiciones climáticas y de cosecha de Cuba es la Yuca (Pérez, et al., 2021). La acetilación de almidón en medio básico acuoso ha sido reportada como un método eficaz, cuando se usa anhídrido acético (AA) como agente esterificante y NaOH como catalizador, con mínimo consumo de agentes. El grado de sustitución (GS) indica el número promedio de sustituciones por UAG. El máximo GS alcanzable es 3, coincidiendo con el número de grupos hidroxilo disponibles de acuerdo a la reactividad de los átomos de carbono C2, C3 y C6, (Spychaj, et al., 2013; Salcedo, et al., 2016; Pérez, et al., 2018).
Siguiendo el procedimiento de la Figura 1, se condujo la modelación de la cinética de acetilación básica acuosa como un caso de modelación fenomenológica. Para ello, las Unidades de Anhidro Glucosa (UAG), constituyentes del almidón, pueden denotarse estructuralmente como (ROH). En medio básico las ROH se activan liberando un hidrógeno (RO-) y permitiendo el ataque sustitutivo de los grupos acetilos provenientes del AA. Como producto principal se obtiene acetato de almidón (RAc) y como producto secundario los restos de AA no sustituidos se hidrolizan a NaAc. Como la formación del éster de almidón tiene tendencia a ser reversible, se obtienen además ácido acético (HAc) y RO-. Adicionalmente el AA tiene tendencia a formar HAc e hidrolizar a NaAc (Olu-Owolabi, et al., 2014).
Se ha demostrado que la velocidad de hidrólisis de los productos polisustituidos es muy baja ante la velocidad de acetilación (De Graaf, et al., 1995). Por esa razón; Pérez, et al. (2018b) propuso, para la evaluación cinética, el mecanismo de dos pasos en paralelo que se muestra en la ecuación (1):
(1)
La velocidad de reacción a volumen constante, resulta para RO- y RAc, según el paso de acetilación en la ecuación (1), como:
(2)
Y para OH- según el paso de hidrólisis en la ecuación (1), como:
(3)
Donde: α, β y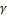 
constituyen el orden de reacción respecto a RO-, AA y OH- respectivamente. En medio acuoso, aunque con diferente fuente y agente, se obtuvo que α=β=γ=1 (De Graaf, et al., 1995). K1 y K2 son las constantes cinéticas de segundo orden para la acetilación y la hidrólisis.
Considerando un análisis parcial de las ecuaciones cinéticas, trabajando en aislamiento, a relación de concentraciones iniciales M=C0 AA/C0 RO - = 10 se obtuvieron expresiones cinéticas que pueden resolverse por el método integral. Expresiones cinéticas simplificadas, para la acetilación y la hidrólisis, se derivan de las ecuaciones (4) y (5) como:
(4)
(5)
Donde: K´1 y K´2 son las constantes cinéticas de pseudo primer orden para la acetilación y la hidrólisis.
Aplicando el método integral de análisis, considerando la ecuación (6), separando variables e integrando, resulta una función de la concentración con el tiempo de reacción en forma lineal como:
(6)
De modo análogo, para la ecuación (7) la solución integrada y lineal de esta expresión cinética es:
(7)
Experimentalmente se procedió a la síntesis de acetato de almidón de bajo GS, determinando el consumo de almidón nativo e iones hidroxilo como función del tiempo de reacción (Pérez, et al., 2018b).
La acetilación se efectuó en condiciones isotérmicas, en un reactor de vidrio, enchaquetado y de 4 L de capacidad efectiva, al que se le acopló un pH metro HANNA. El reactor operó con circulación de agua desde termostato NINGBO SCIENTZ BIOTECHNOLOGY y reflujo de los compuestos volátiles a través de un condensador de vidrio con refrigeración proveniente del propio termostato.
Como reactivos se utilizaron AA Panreac, NaOH Uni-chem y HCl Uni-chem, todos de grado de análisis y 95 % de pureza.
Se prepararon 4 L de solución al 10 % p/v (b. s.) de almidón nativo de yuca, aislado previamente desde la variedad INIVIT Y-93-4. Se mantuvo la agitación y las condiciones isotérmicas a la temperatura de cada experiencia. Se ajustó el pH a 8,0 con solución de NaOH al 3% p/p. Manteniendo el pH entre 8,0 y 8,5 con NaOH al 3% p/p y luego de adicionar lentamente el volumen requerido de AA se dejó reaccionar durante dos horas. Se operó en semicontinuo por adición y medición del flujo volumétrico de disolución de NaOH como determinación indirecta del consumo de iones hidroxilo para mantener el pH constante durante el tiempo de reacción. Transcurrido el tiempo referido, se detuvo la reacción ajustando el pH a 4,5 con disolución de HCl a 0,5 kmol/m3. Se efectuaron extracciones de muestras de 10 mL cada 20 minutos para determinar el avance de la acetilación.
La operación puede ser considerada a volumen constante y se trabajó a concentraciones iniciales C0 AA= 6,38 kmol/m3 y C0 RAc= 0,638 kmol/m3. Cada muestra extraída y el contenido final del reactor fueron lavados tres veces con agua destilada seguido de filtrado a vacío, secado, molinado y tamizado.
La determinación del GS se efectuó por titulación de los residuos acetilos procedentes de un tratamiento alcalino por el contenido de grupos acetilo (% GA) (Guerra, et al., 2008). En la Tabla 1 aparecen los resultados del GS y los consumos de hidroxilos requeridos para mantener el pH constante a ambas temperaturas.
Tabla 1 - GS y consumo de hidroxilos a 25 y 40 °C en la acetilación de almidón nativo de yuca INIVIT Y 93-4.
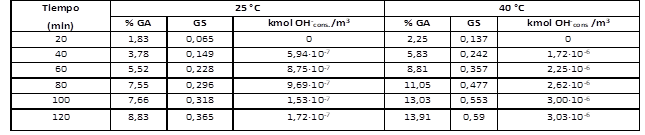
Fuente: Pérez, et al. (2018b).
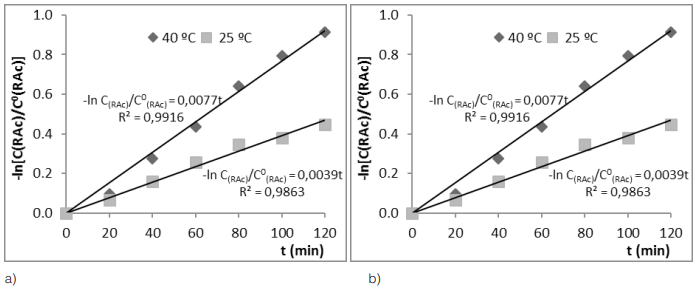
Con los GS se determinaron las CRAC a través de la relación entre ambos deducida y reportada por Pérez, et al. (2018a). A partir de las ecuaciones (6) y (7) se aplicó el método integral de análisis a ambas temperaturas cuyos resultados aparecen en la Figura 2 (a) para la acetilación y en la Figura 2 (b) para la hidrólisis.
Fuente: Pérez, et al. (2018b)
Fig. 2 - Método integral de análisis en la acetilación de almidón nativo de yuca INIVIT Y-93-4 a 25 y 40 °C: a) para la acetilación b) para la hidrólisis.
Se obtuvo un comportamiento lineal con altos coeficientes de regresión de la función de la concentración reflejada en las ecuaciones (6) y (7). Ello demuestra que el mecanismo de reacción presentado en la ecuación (1) es adecuado para describir el transcurso del proceso, donde la acetilación es de primer orden respecto al RO- y al AA y transcurre en paralelo a la hidrólisis del agente, la cual también es de primer orden respecto a los OH- y el AA, siendo dos el orden global de cada paso (Pérez et. al., 2018b).
En la Tabla 2 aparecen las constantes cinéticas de pseudo primer y segundo orden para ambas reacciones a las temperaturas consideradas.
Tabla 2 - Constantes cinéticas del mecanismo de acetilación de almidón nativo de yuca.
| K´ (min-1) | K (m3/kmol min) |
| K´1 a 25 ºC = 0,00390 | K1 a 25 ºC = 6,32∙10-4 |
| K´1 a 40 ºC = 0,00778 | K1 a 40 ºC = 1,26∙10-3 |
| K´2 a 25 ºC = 0,00771 | K2 a 25 ºC = 1,25∙10-3 |
| K´2 a 40 ºC = 0,03500 | K2 a 40 ºC = 5,67∙10-3 |
Fuente: Pérez, et al. (2018b).
Las constantes de pseudo primer y primer orden para la acetilación son de magnitud inferior a las obtenidas acetilando almidón directamente disuelto en AA por Guerra, et al. (2008), pero existen diferencias considerables en el material de partida, las temperaturas de experimentación y la composición del medio.
Considerando los factores de frecuencia y energía de activación anteriormente reportados para este proceso por Pérez (2018), los modelos cinéticos para la acetilación básica acuosa del almidón nativo de yuca, con la temperatura en K, se muestran en las ecuaciones (8), (9) y (10) como:
(8)
(9)
(10)
Las diferencias entre el orden de magnitud de la COH - y la del resto de los componentes y los modelos cinéticos obtenidos, muestran que el efecto determinante en la velocidad de acetilación de almidón de yuca es la COH -. Ese efecto se aprecia claramente, analizando la tendencia de las velocidades de arranque de la reacción, en función del pH inicial del medio, y la selectividad a diferentes valores de pH presentada por Pérez, et al. (2018b).
Atendiendo a los resultados cinéticos, en la acetilación del almidón nativo, estos procesos deben desarrollarse en condiciones básicas moderadas donde se logra la activación efectiva de las UAG, pero no se desarrollan de manera apreciable los procesos de hidrólisis del AA (Pérez, et al., 2018b). Por otra parte, se ha demostrado que en los almidones gelatinizados existe una ruptura parcial de las UAG que facilita la sustitución nucleofílica respecto a los nativos (Lefnaoui & Moulai, 2015).
Por las razones anteriores, se modeló la cinética del material pregelatinizado en medio básico moderado, considerando solamente la reacción de acetilación descrita en la ecuación (1). Integrando en la ecuación (4), sin considerar exceso de AA y transformando resulta la función lineal de la concentración con el tiempo de reacción:
Considerando que K1 es la constante cinética y M es la relación molar de concentraciones en la alimentación como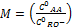 
. Evaluando la ecuación integrada (11) entre los límites M y 
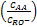y graficando 
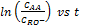resulta una línea recta de pendiente 
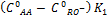e intercepto ln M, si los datos se ajustan al orden de reacción considerado (Levenspiel, 1999).
El procedimiento experimental se efectuó en condiciones y equipos similares al almidón nativo, pero en operación discontinua, partiendo de material pregelatinizado a Co RO -= 0,638 kmol/m3 y Co AA= 1,06 kmol/m3. Los resultados de la determinación del % GA y los GS por el método de Guerra, et al. (2008), así como la CRAc determinada a partir de la relación deducida y reportada previamente (Pérez, et al., 2018a), aparecen reflejados en la Tabla 3.
Tabla 3 - Resultados del estudio cinético a 25 y 40 °C para almidón pregelatinizado de yuca INIVIT Y-93-4.
| 25°C | 40°C | |||||
|---|---|---|---|---|---|---|
| t (min) | % GA | GS | CRAc (kmol/m3) | %GA | GS | CRAc (kmol/m3) |
| 15 | 2,71 | 0,10 | 0,06 | 4,14 | 0,16 | 0,10 |
| 30 | 3,90 | 0,15 | 0,09 | 9,71 | 0,40 | 0,25 |
| 45 | 5,26 | 0,21 | 0,13 | 12,10 | 0,52 | 0,32 |
| 60 | 7,09 | 0,29 | 0,18 | 13,70 | 0,60 | 0,37 |
| 75 | 7,33 | 0,30 | 0,18 | 15,85 | 0,71 | 0,44 |
| 90 | 9,32 | 0,39 | 0,24 | 16,80 | 0,76 | 0,47 |
| 105 | 10,75 | 0,45 | 0,28 | 17,68 | 0,80 | 0,50 |
| 120 | 12,10 | 0,52 | 0,32 | 18,47 | 0,85 | 0,52 |
Fuente: Pérez, et al. (2018a).
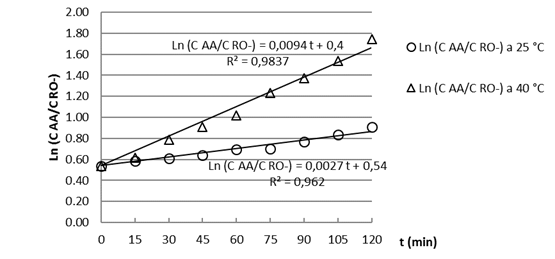
Los resultados de la aplicación del método integral, a ambas temperaturas, son mostrados en la Figura 3. La función de la concentración obtenida en la ecuación (8), se ajustó a una línea recta con adecuados coeficientes de regresión. La reacción es de orden uno respecto a RO- y AA, siendo dos el orden global. Los órdenes de reacción considerados en la definición de la expresión integrada son adecuados. Las pendientes de las rectas obtenidas por aplicación del método integral de análisis permitieron determinar las constantes cinéticas a ambas temperaturas, resultando K1 a 25°C = 6,1 · 10-3 m3/kmol min y K1 a 40°C = 2,13 · 10-2 m3/kmol min.
Fuente: Pérez, et al. (2018a)
Fig. 3 - Método integral de análisis para la acetilación de almidon pregelatinizado de yuca INIVIT Y-93-4 a pH = 8 y temperaturas 25 y 40 °C.
Analizando la relación entre las constantes de velocidad para la acetilación en condiciones acuosas y básicas moderadas evaluadas a 40 °C se obtiene que:
La ecuación 12, demuestra que la velocidad de acetilación es 17 veces superior cuando se parte de material pregelatinizado por lo cual es más ventajoso acetilar a escala industrial material previamente gelatinizado.
Para las constantes cinéticas y temperaturas antes referidas y utilizando la expresión de Arrhenius, se determinó que la energía de activación requerida para la acetilación de almidón pregelatinizado de yuca de la variedad INIVIT Y-93-4 es Epregelatinizado= 64 613,6 J/mol y el factor de frecuencia es K0-pregelatinizado= 1,306 · 109 m3/kmol min (Pérez, 2018).
Con ello, el modelo cinético para la acetilación de almidón pregelatinizado en medio básico acuoso moderado, con la temperatura en K, se expresa a través de la ecuación 13, como:
Sustituyendo en la ecuación de diseño de un reactor de mezcla perfecta (Levenspiel, 1999), se obtiene el modelo global del reactor continuo con agitación, donde se efectúa la acetilación de almidón pregelatinizado de yuca en medio básico acuoso moderado, expresa la relación del tiempo espacial (τ) con el GS, la temperatura (en K) y las concentraciones iniciales de los reactantes como:
El modelo de la ecuación 14 refleja que el tamaño del reactor para efectuar la acetilación de almidón pregelatinizado de yuca en medio básico acuoso es menor cuando se incrementan M y la temperatura. Las condiciones restrictivas de ambos parámetros responden a criterios económicos y medio ambientales por lo que la expresión que relaciona a τ con GS y la temperatura es un punto de partida en la determinación de las condiciones óptimas de este proceso y ha sido utilizada, con muy buenos resultados, para diseñar una instalación industrial para procesar 8 tyuca/d, obteniendo 3,12 talmidón gelatinizado acetilado/d en una secuencia tecnológica que inserta las etapas de gelatinización, acetilación y secado por aspersión en el esquema tecnológico del almidón nativo vía mecanizada (Pérez, 2018).
Conclusiones
Para la modelación matemática de reactores es necesario tener en cuenta la complejidad de los procesos existentes con etapas químicas y difusionales, diferentes tipos y características de contacto entre las fases, catálisis heterogénea y reacciones múltiples. Para obtener modelos efectivos de reactores químicos y biológicos, es preciso considerar factores de proceso como la temperatura, las concentraciones y la naturaleza y propiedades físico químicas de los compuestos presentes. Factores como el pH, la reología, la existencia de catalizadores sólidos o biocatalizadores inmovilizados en diferentes soportes, el equilibrio químico y la distribución de producto también definen las características más importantes del modelo.
La metodología presentada constituye una guía metodológica para la modelación matemática de reactores químicos y biológicos y considera la modelación por vía fenomenológica, por vía estadística y la combinación de ambas opciones. La modelación fenomenológica requiere el auxilio de métodos estadísticos tanto en el tratamiento de datos operacionales e históricos como para el diseño de experimentos cinéticos. Cuando se utiliza la modelación estadística es posible evaluar datos de operación o diseñar experimentos adecuados en condiciones experimentales o de proceso. El uso de métodos matemáticos automatizados facilita la solución, simulación y optimización de los modelos propuestos, sobre todo cuando se consideran patrones pseudo-homogéneos o heterogéneos.
El objetivo principal de la modelación de un reactor químico o biológico, es determinar las condiciones óptimas o la región de operación óptima. La disponibilidad de un modelo operacional efectivo facilita además el diseño, la evaluación y el escalado.
El procedimiento propuesto se ha utilizado con éxito en la obtención del modelo fenomenológico que caracteriza el reactor de acetilación en la producción de almidón acetilado y gelatinizado acetilado a partir de yuca y en el desarrollo de otros procesos de la industria alimentaria y química cubana en años recientes.
El modelo global del reactor de acetilación de almidón pregelatinizado de yuca de la variedad INIVIT Y-93-4, operando en medio básico acuoso y utilizando anhídrido acético como agente esterificante, tiene en cuenta el mecanismo de acetilación, la distribución más favorable del producto y los efectos de pH sobre ella, los efectos térmicos sobre la cinética, las relaciones de alimentación y la conversión deseada, expresada en función del grado de sustitución nucleofílica.
