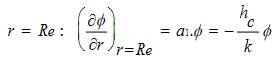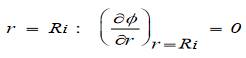Introducción
El crecimiento anual del mercado mundial del plástico hasta 2032 se prevé en el entorno del 7.2 % y su impacto económico se pronostica en los $2 865 billones de dólares con crecimientos similares al igual que en las emisiones de CO2, ya que para esa fecha no está previsto aún que la energía eléctrica sea totalmente de fuentes renovables y aunque así sea siempre será provechoso el ahorro. Esto justifica todos los esfuerzos que se realizan para lograr los mayores rendimientos productivos y energéticos. (Plan de Negocios, 2019). Ver anexos 1,2 y 3.
Este crecimiento de la industria del plástico tiene un impacto negativo en el deterioro ambiental a nivel mundial, tema de constante preocupación y que ha desencadenado múltiples esfuerzos por encontrar sus determinantes. Su difícil reciclaje y su baja capacidad de degradación tienen como consecuencia su acumulación en cantidades que generan además un efecto negativo sobre los seres vivos, ya sea por ingestión o por toxicidad (Bollaín & Vicente, 2020; Vinueza et al., 2021).
En la actualidad, los plásticos se producen de forma masiva para dar cabida a nuevas necesidades, lo que promueve un consumo incesante de los mismos. La mayor parte de los materiales plásticos producidos se emplean en la fabricación de productos de un solo uso como envases o botellas (Jaén et al., 2019).
Cuba no está exenta de este desarrollo y tiene planes ambiciosos de reducción de las cargas contaminantes al medio ambiente, el cual se encuentra en estos momentos en aproximadamente 0.700 gramos de C02 por cada kW/h producido (Velázquez, 2020).
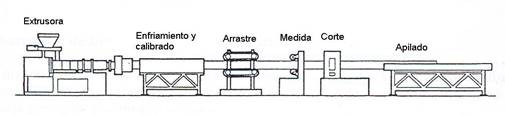
El propio trabajo con los plásticos puede ser también una fuente de contaminación por los procesos que se desarrollan relacionados con el consumo de energía, entre ellos: extrusión, inyección, termo formado, calandrado, espumado y otros. El más utilizado en la producción de tuberías es la extrusión, que se define como un proceso continuo, donde la resina es fundida, por la acción de la temperatura y la fricción, siendo forzada a pasar por un molde, que le proporciona una forma definida, para ser enfriada finalmente y evitar deformaciones permanentes. Se fabrican por este proceso: tubos, perfiles, películas, manguera, láminas, filamentos, pellets y otros. Energéticamente los procesos de transformación de plásticos en general, requieren de un gran aporte de energía, tanto calorífica como mecánica (Jiménez et al., 2015). Por una parte, los plásticos deben calentarse para lograr fundirlos o extruirlos y así poder ser procesados, necesitando para ello aproximadamente el 50% de la energía necesaria para la producción. Posteriormente el producto se enfría, transporta, corta, bobina o peletiza y para ello requiere de aproximadamente del 15 al 25 % de la energía total dedicada a este proceso (Heesen & Wortberg, 2015; Hiesgen et al., 2016).
Los costos operacionales de la energía en estos procesos pueden representar entre el 4 y el 10 % en una planta de transformación de plástico (Novoa, 2009). El tiempo de enfriamiento, toma la mayor parte del total de la producción en cualquier termo proceso plástico y para lograr que los cálculos sean óptimos es necesario el conocimiento de sus propiedades térmicas, como el calor específico, la densidad y la conductividad térmica de los materiales que se procesan (Wesley, 2012). Con el objetivo de controlar los niveles de consumo en los procesos de extrusión, se han realizado diversos estudios, para el mejoramiento de su desempeño energético (Rahman et al., 2018; Krstić & Nikolić, 2018; Quevedo et al., 2021).
El control energético en esta industria, varía en dependencia del tipo de centro de investigación, tecnología utilizada, las empresas y países que producen los bienes materiales y la investigación científica (Jiménez et al., 2019). De ahí que existan índices de consumo de la energía con respecto a la producción en general, por surtidos, ramas, según flujo a la salida de las máquinas, por puestos claves seleccionados en las industrias, entre otros. Estos índices de consumo, han devenido en un indicador de desempeño energético aplicable a sistemas de gestión de la energía basados en la norma internacional que gestiona su implementación en muchas empresas (ISO 50001, 2011, ISO 50002, 2014; Tim et al., 2012; Vargas et al., 2015).
La Fig 1 muestra la línea simplificada de extrusión de tuberías.
Ver extrusora actual (Anexo 4).
Materiales y métodos
Para el trabajo fueron utilizadas líneas de máquinas extrusoras de varios flujos, termómetro industriales SIKA-Matec medición y Ss 304 y medidores de espesores multifuncionales ultrasonidos PCE-TG 100 de 0.8 mm a 225 mm de rangos. Se aplicaron diversos métodos, como son: el método histórico lógico, el método comparativo, el análisis y la síntesis, el tratamiento automatizado de la información, así como, del nivel matemático, el empleo de un método de análisis numérico, en específico el método de solución exacta, condición de contorno isotérmica, para calcular mediante software de avanzada las soluciones exactas y estadísticas, el método de regresión, de varianza y de correlación.
El enfriamiento por extrusión, se produce al salir el sub producto del molde y penetrar en el calibrador que se encuentra en la bañera de enfriamiento. En él debe lograrse a la salida de la misma una determinada temperatura en la superficie interior y exterior de la tubería que evite deformaciones del perfil y afectaciones en la calidad del producto final.
Para alcanzar la temperatura deseada a la salida de la bañera, según el espesor y diámetro de que se trate, se requerirá un determinado tiempo de enfriamiento que dependerá del flujo de material, de sus propiedades termofísicas, nivel de producción dado, de las propiedades del agua de enfriamiento, de la temperatura y régimen de circulación del agua helada, de las dimensiones del producto y de la bañera de enfriamiento (Jiménez et al., 2019). Para este caso fue considerada la temperatura en la superficie de 30⁰C como promedio en general temperatura ambiente y en el interior 60⁰C pues superior a esta se comienzan a perder propiedades mecánicas para su funcionamiento y etapas por las cuales transita el proceso. El trabajo se desarrolla en coordenadas cilíndricas por ser esta la geometría utilizada con las siguientes suposiciones para el modelo: El estado es transitorio, Flujo externo, Transferencia de calor por convección forzada con flujo de calor transversal al tubo. Las mayores temperaturas están en el centro del perfil. El calor transferido para el enfriamiento es considerado por conducción y convección (Jiménez et al., 2017).
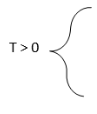
Para conocer el perfil de temperaturas del plástico a lo largo de la bañera de enfriamiento se procede a realizar un balance de calor general en un elemento de volumen diferencial de un tubo infinito con convección en la superficie lateral exterior y aislamiento térmico en la superficie lateral interior, que da como resultado para un tiempo mayor que cero la siguiente encuación para la superficie y para el centro del perfil (ecuaciones 1 y 2).
Y como resultado final después de haber trabajado estas ecuaciones se obtiene la solución general del problema como una combinación lineal de infinitas soluciones de intervalos para los infinitos auto valores λ n como se muestra en la (ecuación 3).
Estas ecuaciones y su desarrollo han sido publicadas por el autor en la Revista Ingeniería Energética del Centro de investigaciones electro energética de la Universidad Tecnológica de Cuba José Antonio Echeverría, CUJAE.
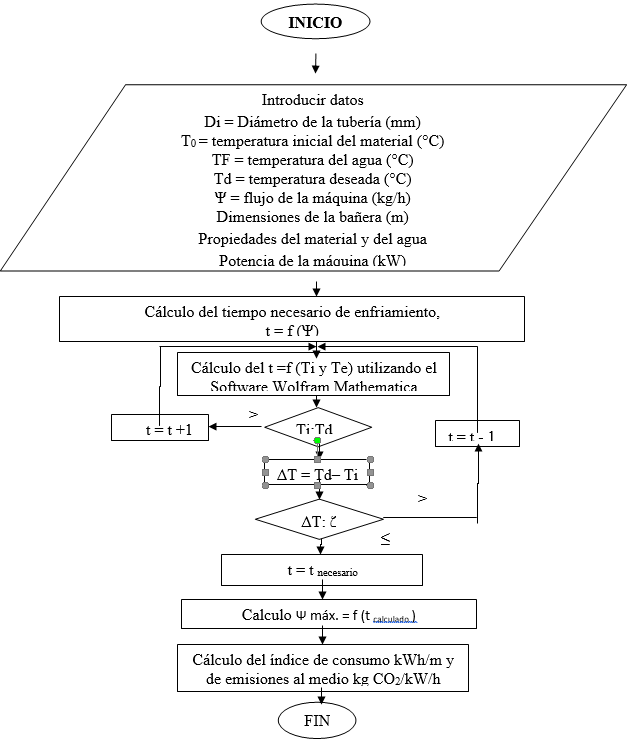
La Fig 2 muestra el algoritmo de cálculo seguido en la investigación.
Realiza el primer cálculo del tiempo necesario según el flujo de la máquina teniendo en cuenta lo establecido por la norma DIN 8062-10 2009, UNE-ISO 2015, en cuanto al peso de la tubería, sus características de diámetro y espesor, seguidamente realiza el cálculo del tiempo que se demora en llegar a la temperatura deseada de la superficie interior o exterior de la tubería, según sea el caso teniendo en cuenta las propiedades termofísicas seleccionadas del material, aumentando o disminuyendo el valor del tiempo hasta alcanzar el parámetro diferencial que se desea de acuerdo a la exactitud planificada mediante la utilización de la herramienta Software Wolfram Matemathica 12.3. Si está dentro del parámetro, será el tiempo necesario para evaluar un nuevo flujo para la máquina y se compara con el anterior, para la toma de decisiones productivas y energéticas.
Por último, realiza el cálculo del índice de consumo y la emisión de CO2 según sea el caso comparándose los resultados con los del flujo según norma.
El procedimiento utilizado para el cálculo de los resultados según el tipo de propiedad termofísicas fue el de mantener una variable y el resto constante, teniendo en cuenta que los resultados anteriores existen para un tipo de materia prima determinada (Jiménez et al., 2018).
Resultados y discusión
El comportamiento de las propiedades térmicas utilizadas según los modelos matemáticos y software aplicados presentan el siguiente comportamiento siento tomado como promedio de emisiones al medio ambiente la cifra de 0.700 kg de C02/ kW consumido (Tabla 1).
Tabla 1 - Propiedades de la materia prima utilizadas comercialmente.
| ρ = Densidad del material (kg/m3) | K= Conductividad térmica W/(m·K) | Cp= calor específico J/(kg·⁰C) |
| 1 420 | 0,25 | 1 500 |
| 1 420 | 0,20 | 1 260 |
| 1 400 | 0,22 | 1 370 |
| 1 300 | 0,20 | 1 300 |
| 1 200 | 0,18 | 1 100 |
Fuente: Elaboración propia, 2022.
Con estas propiedades se realizan las corridas según los espesores y diámetros en estudio para determinar sus relaciones y aportes en los resultados productivos, energéticos y su impacto en las emisiones al medio ambiente Para este caso, tubería de 90 y 110 mm de diámetro y variados espesores. El índice de consumo fue calculado con el valor productivo de las propiedades físicas seleccionadas, para máquinas de 150, 200, 270 y 450 kg/h de flujo escogiéndose los flujos de 200 y 270 kg/h con una potencia de 86 y 121 kW respectivamente por ser estas las más utilizadas (Jiménez et al., 2019).
El primer reporte corresponde al comportamiento de las variaciones del calor específico, mientras se mantienen constantes el resto de las propiedades (k y ρ) y los resultados se muestran en la Tabla 2, donde (1) espesor de la tubería, (2) peso del metro de tubería, (3) temperatura deseada para este caso, (4) temperatura en el radio interior, (5) temperatura en el radio exterior, (6) tiempo en segundos en alcanzar las temperaturas deseadas en radio interior y exterior en segundos, (7) y a partir del (8), (9), (10) y (11) corresponden a los flujos de diseño de las máquinas.
Observar que la temperatura deseada para todos los casos es de 30 grados para la superficie, pero en la medida que aumenta el espesor aumenta la temperatura en la superficie interior. Para espesores gruesos en que la temperatura interior sobre pasa los 600C se invierte el control y se toma como referencia la interior, pues como ya se explicó a partir de esta temperatura este material comienza a perder propiedades mecánicas que afectan el resto del proceso.
Tabla 2 - Comportamiento productivo variando Cp., k y ρ constantes, tubería 90 mm de diámetro.
|
Espesor mm (1) |
Kg/m P:F (2) |
TD ⁰C (3) |
TRi ⁰C (4) |
TRe ⁰C (5) |
t. Seg (6) |
Flujo P:F m/8h (7) |
Flujo150 m/8h (8) |
Flujo200 m/8h (9) |
Flujo270 m/8h (10) |
Flujo450 m/8h (11) |
| Cp. = 1 100 ρ = 1 420 k = 0,22 | ||||||||||
| 1,8 | 0,785 | 30 | 41 | 30 | 70 | 3 295 | 1 528 | 2 037 | 2 751 | 4 585 |
| 2,2 | 0,976 | 30 | 43 | 30 | 89 | 2 580 | 1 230 | 1 640 | 2 213 | 3 689 |
| 2,7 | 1,112 | 30 | 47 | 30 | 109 | 2 111 | 1 031 | 1 374 | 1 855 | 3 092 |
| Cp. = 1 200 ρ = 1 420 k = 0,22 | ||||||||||
| 1,8 | 0,785 | 30 | 41 | 30 | 76 | 3 021 | 1, 528 | 2, 037 | 2 751 | 4 585 |
| 2,2 | 0,976 | 30 | 43 | 30 | 97 | 2 365 | 1, 230 | 1 640 | 2 213 | 3 689 |
| 2,7 | 1,112 | 30 | 47 | 30 | 119 | 1 935 | 1 031 | 1 374 | 1 855 | 3 092 |
| Cp. = 1 370 ρ = 1 420 k = 0,22 | ||||||||||
| 1,8 | 0,785 | 30 | 41 | 30 | 87 | 2 645 | 1 528 | 2 037 | 2 751 | 4 585 |
| 2,2 | 0,976 | 30 | 43 | 30 | 111 | 2 071 | 1 229 | 1 639 | 2 213 | 3 853 |
| 2,7 | 1,112 | 30 | 47 | 30 | 136 | 1 695 | 1 030 | 1 374 | 1 855 | 3 229 |
| Cp. = 1 500 ρ = 1 420 k = 0,22 | ||||||||||
| 1,8 | 0,785 | 30 | 41 | 30 | 95 | 2 416 | 1 528 | 2 037 | 2 751 | 4 585 |
| 2,2 | 0,976 | 30 | 43 | 30 | 122 | 1 892 | 1 230 | 1 640 | 2 213 | 3 689 |
| 2,7 | 1,112 | 30 | 47 | 30 | 149 | 1 547 | 1 031 | 1 374 | 1 855 | 3 092 |
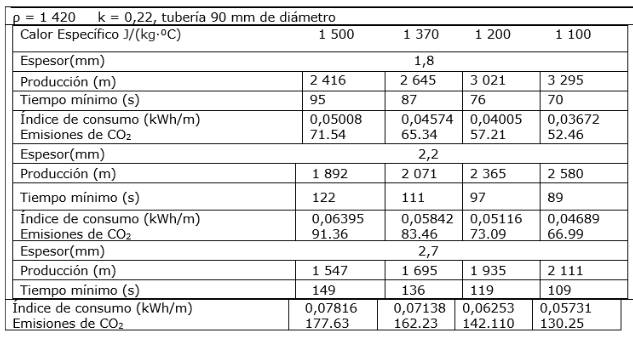
La Tabla 3 muestra el resumen de la Tabla 2 del comportamiento de esta propiedad.
El comportamiento gráfico se muestra en la Fig. 3.
Se aprecia en la figura como en la medida que aumenta el calor especifico, disminuye la producción y aumenta el índice de consumo energético.
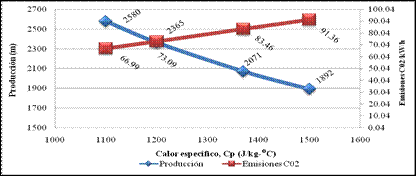
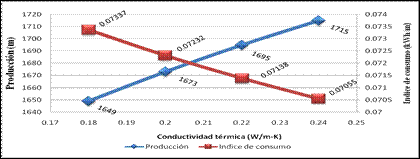
La Fig. 4 muestra la relación entre producción, calor específico y las emisiones de C02 para 2.2 mm de espesor.
Se aprecia en la figura como a medida que aumenta el calor específico disminuye la producción que trae consigo el aumento del índice de consumo y por consiguiente las emisiones de C02 al medio ambiente.
La Fig. 5 muestra la relación entre el tiempo necesario con el calor específico para 2.2 mm de espesor.
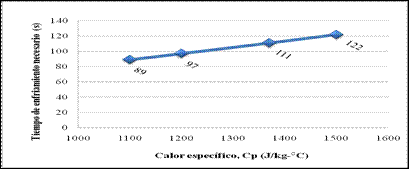
Fig. 5 - Relación entre el tiempo necesario con el calor específico para 2.2 mm de espesor. Fuente: Elaboración propia, 2022.
Se aprecia como en la medida que aumenta el calor específico aumenta también el tiempo de enfriamiento aumentando con esta relación los índices de consumo energético y las emisiones al medio ambiente.
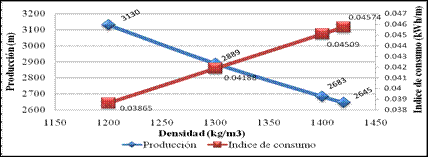
Siguiendo este mismo procedimiento se obtuvieron para la densidad y la conductividad térmica las siguientes gráficas. Para la densidad (Fig 6):
La figura muestra como en la medida que aumenta la densidad disminuye la producción y aumentan los índices de consumo, en un comportamiento que se asemeja al calor específico, pero con menor sensibilidad.
La Fig 7 muestra la relación entre producción, densidad y emisiones al medio ambiente para 1.8 mm de espesor.
La gráfica muestra como en la medida que aumenta la densidad crecen las emisiones de C02 al medio ambiente.
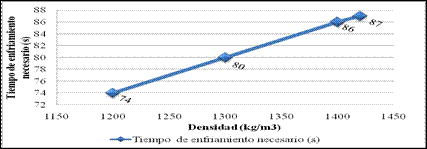
En la Figura 8 se puede observar la relación entre producción y tiempo necesario.
El tiempo necesario para la producción crece en la medida que aumenta la densidad, por lo que aumentan también los índices de consumo, las emisiones al medio ambiente y disminuye la producción. Comportamiento para la conductividad térmica.
En la Fig 9 se puede observar la relación producción y el índice de consumo para 2.7 mm de espesor.
Se aprecia en la figura como la conductividad térmica tiene un comportamiento en la producción e índices de consumo contrario al calor específico y la densidad pues en la medida que aumenta disminuyen los índices de consumo y aumenta la producción.
En la Fig 10 se puede observar la relación entre producción, conductividad térmica con las emisiones de C02 para 2.7 mm de espesor.
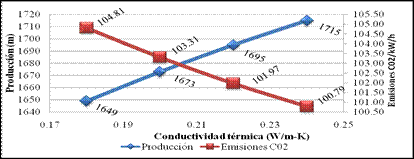
Fig. 10 - Relación entre producción, conductividad térmica con las emisiones de C02 para 2.7 mm de espesor.
Muestra como en la medida que aumenta la conductividad térmica disminuyen las emisiones de C02 al medio ambiente y se alcanza una mayor producción.
En la Fig. 11 se puede observar la relación entre tiempo necesario y la conductividad térmica para 2.7 mm de espesor .
Se aprecia como en la medida que aumenta la conductividad térmica disminuye el tiempo necesario que implica una disminución de los índices de consumo las emisiones al medio y una elevación de la producción.
En el trabajo fueron aplicados métodos estadísticos según el software Startgraphics Centurion XV que proporcionó un modelo matemático para el cálculo del comportamiento de estas propiedades. (ρ, Cp., K), utilizando como valores máximos y mínimos los correspondientes al rango normado para estas propiedades en las materias primas utilizadas comercialmente en la Tabla 1.
Considerando como caso de estudio la tubería de 110 mm con espesor 1,8 mm se determina el tiempo de enfriamiento para una máquina de 270 kg/h, según 27 combinaciones de valores de las variables de entrada.
El modelo estadístico de interés que nos proporciona es un modelo de superficie representado por una función, la cual está compuesta por un término constante, términos lineales, términos de interacción entre variables y términos cuadráticos. La expresión matemática puede escribirse como: (ecuación 4)
Donde: K0…K9 son los coeficientes de la ecuación y ρ, Cp., y k son las propiedades físicas de la materia prima definidas en la Tabla 1.
A partir de este modelo se aplica el método de regresión obteniéndose los resultados siguientes (Tabla 4).
Tabla 4 - Coeficiente de regresión para tiempo de enfriamiento necesario.
|
|
457,968 |
|
|
-0,324363 |
|
|
-0,163624 |
|
|
-1187,47 |
|
|
0,0000671258 |
|
|
0,000112311 |
|
|
0,329798 |
|
|
0,0000203056 |
|
|
0,163611 |
|
|
1 106,17 |
Puede apreciarse existen tres coefientes que aportan elementos negativos a la regresión y por tanto la ecuación del modelo de superficie ajustado es: ecuación 5
El objetivo que se persigue con esta experimentación es descubrir los efectos individuales y conjuntos que varios factores ejercen sobre el tiempo de enfriamiento en el proceso de extrusión de tuberías plásticas bajo estudio. El resultado del análisis de regresión es el siguiente (Tabla 5):
Tabla 5 -Análisis de Varianza para tiempo de enfriamiento necesario.
| Fuente | Suma de Cuadrados | Gl | Cuadrado Medio | Razón-F | Valor-P |
| A:ρ | 970,936 | 1 | 970,936 | 157,26 | 0,0000 |
| B:Cp | 3 594,39 | 1 | 3 594,39 | 582,18 | 0,0000 |
| C:k | 98,9356 | 1 | 98,9356 | 16,02 | 0,0009 |
| AA | 3,95823 | 1 | 3,95823 | 0,64 | 0,4344 |
| AB | 73,2602 | 1 | 73,2602 | 11,87 | 0,0031 |
| AC | 14,2136 | 1 | 14,2136 | 2,30 | 0,1476 |
| BB | 3,95823 | 1 | 3,95823 | 0,64 | 0,4344 |
| BC | 11,564 | 1 | 11,564 | 1,87 | 0,1889 |
| CC | 5,94679 | 1 | 5,94679 | 0,96 | 0,3401 |
| Error total | 104,958 | 17 | 6,17399 | ||
| Total (corr.) | 4 882,12 | 26 |
Para este caso, cuatro efectos tienen un valor-P menor que 0.05 indicando que son significativamente diferentes de cero con un nivel de confianza del 95.0%. Estos son los efectos principales para ρ, Cp., k, y el efecto de interacción de ρ y Cp. El diagrama de Pareto de la figura 12 también muestra estos resultados.
Al aplicar el método de varianza se obtienen los siguientes resultados.
R-cuadrada = 97.8502 porciento
R-cuadrada (ajustada por g.l.) = 96.712 porciento
Error estándar del est. = 2.48475
Error absoluto medio = 1.30731
Estadístico Durbin-Watson = 1.83893 (P=0.2424)
Auto correlación residual de Lag 1 = 0.0237125
En la aplicación de la matriz de correlación para los efectos estimados para el tiempo de enfriamiento necesario muestra el grado de confusión entre los efectos. Para este caso el resultado fue un diseño perfectamente ortogonal pues mostró una matriz diagonal con 1´s en la diagonal y 0´s fuera de ella. Cualquier término distinto de cero implica que los estimados de los efectos correspondientes a esa fila y columna estarán correlacionados. En este caso, no hay correlación entre ninguno de los efectos. Esto significa que se obtuvieron estimados ¨limpios¨ para todos esos efectos (Tabla 6).
Tabla 6 - Matriz de correlación para los efectos estimados para el tiempo de enfriamiento necesario.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | promedio | 1.0000 | 0.0000 | 0.0000 | 0.0000 | -0.5345 | 0.0000 | 0.0000 | -0.5345 | 0.0000 | -0.5345 |
| (2) | A:Rho | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (3) | B:Cp | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (4) | C:k | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (5) | AA | -0.5345 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (6) | AB | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (7) | AC | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 |
| (8) | BB | -0.5345 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| (9) | BC | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| (10) | CC | -0.5345 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
La siguiente Tabla 7 muestra una facción de las 27 combinaciones del experimento para demostrar el resultado, según los valores obtenidos entre ambos softwares comprobándose la cercanía entre los valores observados que son los obtenidos por el modelo matemático del Wolfram Mathematica 12.3 y el obtenido por el estadístico Startgraphics Centurion XV que son los ajustados, inferior al 95% y superior al 95%.
Tabla 7 - Resultados estimados para tiempo de enfriamiento necesario según las 27 combinaciones.
| Observados | Ajustados | Inferior 95.0% | Superior 95.0% | |
|---|---|---|---|---|
| Fila | Valores | Valores | para Media | para Media |
| 1 | 83,54 | 83,5445 | 83,5178 | 83,5713 |
| 2 | 90,55 | 90,577 | 90,5444 | 90,6097 |
| 3 | 97,01 | 97,0059 | 96,9826 | 97,0292 |
| 4 | 76,52 | 76,5131 | 76,4805 | 76,5458 |
| 5 | 104,35 | 104,364 | 104,331 | 104,396 |
| 6 | 102,53 | 102,54 | 102,514 | 102,567 |
| 7 | 88,98 | 88,967 | 88,9403 | 88,9938 |
| 8 | 90,43 | 90,4379 | 90,4111 | 90,4646 |
| 9 | 105,15 | 105,163 | 105,139 | 105,186 |
| 10 | 87,74 | 87,7248 | 87,6922 | 87,7575 |
| 11 | 98,72 | 98,7226 | 98,6993 | 98,7459 |
| 12 | 82,08 | 82,0637 | 82,0404 | 82,087 |
| 13 | 111,93 | 111,949 | 111,926 | 111,973 |
| 14 | 87,63 | 87,6306 | 87,6039 | 87,6574 |
| 15 | 119,64 | 119,645 | 119,613 | 119,678 |
| 16 | 110,37 | 110,365 | 110,338 | 110,391 |
| 17 | 101,11 | 101,085 | 101,052 | 101,117 |
| 18 | 80,94 | 80,9506 | 80,9239 | 80,9774 |
| 19 | 113,91 | 113,902 | 113,875 | 113,929 |
| 20 | 121,33 | 121,359 | 121,332 | 121,386 |
Definición gráfica del comportamiento estadístico del experimento para tiempo de enfriamiento necesario (Fig 12).

Fig. 12 - Carta de Pareto estandarizada para tiempo enfriamiento necesario, muestra como efectivamente el efecto contrario del proceso lo aporta la conductividad térmica.
En resumen se aprecian comportamientos diferentes en cada una de las propieades estudiadas con respecto a la producción, índices de consumo y por consiguientes las emisiones al medio ambiente.
En la Fig 13 se muestra la superficie que ilustra cómo efectivamente, para un valor de k determinado con valores mínimos de Cp. y de ρ se consigue el menor tiempo de enfriamiento necesario de la tubería en la bañera y por lo tanto la menor emisión de de contaminantes al medio.
La figura anterior muestra la relación que existe entre las propiedades en el proceso con respecto a una conductividad térmica seleccionada, para los tiempos de enfriamiento necesarios. Refleja que en la medida que crece la densidad aumenta el tiempo de enfriamiento necesario en la bañera de enfriamiento como fue descrito en el capítulo anterior, donde se realizó el análisis del comportamiento de esta propiedad, de igual forma sucede con el calor específico que presenta una situación similar, pero como se observa con una mayor sensibilidad en el proceso, en ambos casos en la medida que crecen sus magnitudes aumentan los tiempos de enfriamiento necesarios en la bañera, que conllevan a una disminución de los rendimientos productivos y un aumento en los índices de consumo; ratificando también los resultados del capítulo anterior.
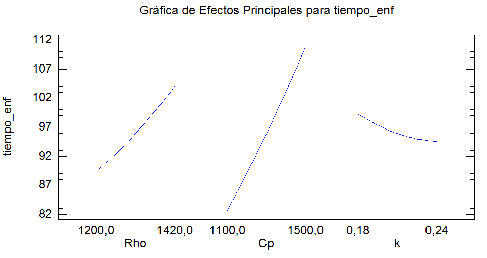
A continuación, se procede a realizar una gráfica de efectos principales como se muestra en la Figura 14, con el fin de interpretar el comportamiento de cada una de las variables en estudio con respecto a la variable independiente y el tiempo enfriamiento necesario, que para este caso define la eficiencia del proceso y ratifica lo planteado; reforzando el concepto de modelo híbrido que contribuye a facilitar los cálculos con el nuevo modelo estadístico.
De la figura anterior se puede interpretar que la variable ρ tiene un comportamiento creciente según su magnitud con relación al aumento en el tiempo de enfriamiento necesario, lo que significa que a medida que aumenta la densidad del material, se necesita mayor tiempo de enfriamiento para alcanzar la temperatura deseada. El calor específico se comporta de manera similar, un incremento de este conlleva necesariamente al aumento del tiempo de enfriamiento necesario. Sin embargo, un incremento en la conductividad produce un decrecimiento en el tiempo de enfriamiento necesario.
Conclusiones
El trabajo demuestra como existe un comportamiento diferente en cuanto al tiempo necesario para el enfriamiento en un proceso de extrusión de tuberías plásticas según las temperaturas deseadas en relación con tres elementos fundamentales: la producción, los índices de consumo y las emisiones al medio ambiente a través de las propiedades termofísicas seleccionadas.
El calor específico y la densidad a medida que aumenta su magnitud aumenta el tiempo necesario en la producción y por consiguiente los índices de consumo, provocando un aumento de las emisiones de CO2 al medio ambiente, el calor específico con una mayor sensibilidad, teniendo la conductividad térmica un comportamiento contrario.
De lo anterior se desprende la importancia de mantener procesos productivos contralados, usando los avances informáticos de la ciencia y la técnica para mejorar la eficiencia de estos procesos y sobre todo los vinculados directamente con la energía, pues a corto plazo no se vislumbra una solución totalmente renovable de estas fuentes y aunque así sea la eficiencia es la mejor forma de ahorro; logrando mejores resultados en la protección al Medio Ambiente.