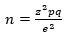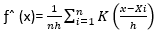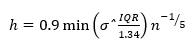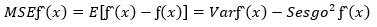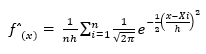Introducción
A partir de la primera revolución industrial, la eficiencia adquirió mayor trascendencia en los procesos económicos. A lo largo de la historia se ha ido remplazando un conjunto de técnicas que permitan optimizar los procesos. En las últimas décadas se ha intensificado la investigación e inversión en el área de la robótica aplicada a la industria en procesos mecánicos y repetitivos.
Cardoso et al. (2017) puntualizan que, debido al incesante desarrollo tecnológico y la automatización de los procesos industriales, la mayoría de las grandes industrias, se han visto obligadas a insertar sistemas robóticos que favorezcan la disminución de los costes de producción y la ampliación de las capacidades físicas. Destacan además que el crecimiento de la robotización industrial ha movido al mundo de la investigación para crear máquinas con más funcionalidades que ayuden a mejorar la eficiencia energética y la capacidad de adaptación a las condiciones del entorno de trabajo, así como incrementar la seguridad en las operaciones y la producción de bienes.
La utilización de sistemas robóticos trae considerables ventajas en entornos industriales relacionadas con el incremento de la eficacia, la rapidez de procesos mecánicos y de la productividad, lo que contribuye a mejorar la competitividad (Damas, 2019). Posibilita que las empresas mejoren su desempeño al reducir los errores y mejorar la calidad y la velocidad (Porcelli, 2020).
La utilización de robots se justifica por una reducción de costes y por su mayor rendimiento en ciertas tareas repetitivas o de alta precisión. Entre las aplicaciones robóticas actuales destacan los procesos de montaje en la industria del automóvil, la selección de productos en la industria alimentaria y el transporte autónomo en logística (Pérez, 2022). Ello redunda en la optimización de tiempo respecto a lo que un operario humano puede lograr.
Considerando que un buen desempeño logístico puede tener un efecto positivo sobre el crecimiento económico es interesante reflexionar sobre las estadísticas al respecto. En el caso de Ecuador el Índice de desempeño logístico calculado para el 2018fue de 2.88, valor bastante alejado de las mejores posiciones: la mejor posición mundial la ocupó Alemania con 4.20; la mejor posición en América Estados Unidos con 3.89; la mejor posición en Centroamérica fue para Panamá con 3.28 (Jean-François et al., 2018 citado en Estévez & Bonilla, 2020). Lo anterior denota la necesidad del empleo de tecnologías que contribuyan a optimizar los procesos donde obviamente la robótica tiene un importante papel.
El empleo de la robótica implica la necesidad de utilizar mecanismos controladores que aseguren la fiabilidad del robot. En este sentido, los controladores permiten el cálculo matemático para el control de diferentes tipos de máquinas y de procesos, de modo que las articulaciones del robot alcancen la posición deseada en el área de trabajo (Craig, 2006). Razón por la cual se le puede dar un sin número de aplicaciones dentro del tratamiento de las mercancías, en dependencia del actuador final implementado en el prototipo, ya sea una cámara para el control de calidad o reconocimiento de objetos para clasificación (Arpenti et al., 2020), una pinza para la manipulación de mercancías nocivas o tóxicas, ventosas para desensamblaje, etc.
Dada la importancia de que el controlador cumpla su función, se hace necesario el empleo de dos controladores para que en caso de que el controlador principal falle, el otro controlador pueda tomar el control del prototipo lo más rápido posible y completar la trayectoria prevista. En este sentido se requiere validar el empleo de dos controladores de un prototipo de robot cartesiano de dos grados de libertad para el proceso de la logística de mercadería, objetivo que se persigue en la presente investigación. La confiabilidad de los controladores se estima a través de una función de densidad que caracteriza el comportamiento de los tiempos requeridos para la reconfiguración.
Desarrollo
En la actualidad, el desarrollo de prototipos robóticos se da a gran escala, aplicados a diversas áreas del conocimiento, ya sea en la medicina para abordajes endoscópicos o en la agricultura para rociar fertilizantes, pesticidas en los campos, en los procesos de montaje en la industria del automóvil, en la selección de productos en la industria alimentaria y el transporte autónomo en logística. En la industria manufacturera los robots realizan actividades de montaje, dispensación, manipulación, transformación y soldadura.
En el campo de la logística el empleo de la robótica está cada vez más enraizado, ya que los robots están siendo utilizados para optimizar el flujo de las cargas. La progresiva complejidad del almacén y la demanda de operativas ágiles y eficientes unido a la necesidad de reducir costos y optimizar los procesos para mejorar la competitividad han propiciado el uso de robots en muchas de las operaciones logísticas más comunes como son: almacenamiento, preparación de envíos o paquetes, embalaje de productos, carga y descarga, distribución autónoma de los despachos.
De esta forma, la robótica en logística emplea diferentes máquinas o robots que agilizan los procesos, rebajan costos logísticos y minimizan el riesgo de accidentes. En función de las operativas, MECALUX (2022) plantea que se pueden utilizar los siguientes robots:
Robots logísticos como los sistemas automáticos de carga y descarga de camiones que permiten introducir y retirar las tarimas de los camiones de forma robotizada y transportadores automáticos para las tareas de recepción y expedición de mercancía.
Robots de almacenamiento que incluye los transelevadores monocolumna, bicolumna, y trilaterales automáticos. Estos robots logísticos se desplazan a lo largo y alto de los pasillos de almacenamiento para ubicar y extraer las tarimas o cajas de los racks de manera automática.
Para la preparación de pedidos se emplean los llamados almacenes automatizados para cajas y los brazos robóticos, encargados de extraer los productos de una ubicación para ordenarlos y colocarlos en otro sitio.
Los transportadores para tarimas, los transportadores para cajas, las electro vías y los vehículos de guiado automático son soluciones para el transporte interno de mercancías.
Se estudia el uso de drones para transportar y entregar por vía aérea los pedidos que los clientes han solicitado.
Los robots como tal solo tienen sentido si el propósito con el que fueron construidos es el de ayudar a mejorar las condiciones de vida del ser humano, ya sea para relevarlo de tareas peligrosas, rutinarias o a su vez en trabajos que requieren de mucha precisión. Existen al menos tres tipos de robots: 1) manipuladores, o brazos robóticos los cuales están físicamente anclados en su lugar de trabajo y se desplazan en cadena para posicionar a los efectores en cualquier lugar del entorno de trabajo; 2) robots móviles son aquellos que se desplazan utilizando ruedas, piernas o mecanismos similares; y 3) El tercer tipo es un híbrido: un robot móvil equipado con manipuladores (Porcelli, 2020).
A su vez los robots industriales se pueden clasificar de acuerdo a diferentes criterios. Según el tipo de movimiento se clasifican por grados de libertad; el número de grados de libertad se refiere al número mínimo de parámetros que necesitamos especificar para determinar completamente la velocidad de un mecanismo o el número de reacciones de una estructura; de acuerdo a la arquitectura se distinguen los seriales si su cadena cinemática es un lazo abierto y los paralelos si contiene una o varias cadenas en lazos cerrados; según la interacción con las personas robots pueden ser colaborativos o no (Eker & Eker, 2018).
De acuerdo con Rodríguez et al. (2009) la programación de las tareas que pueden realizar comprende dos grandes etapas: primero se generan las trayectorias y posteriormente es aplicado el control de trayectorias para cumplir las tareas. De esta manera, el empleo de la robótica implica la necesidad de utilizar mecanismos controladores que aseguren la fiabilidad del robot. En los procesos de transporte y manipulación de mercancías, la fiabilidad del prototipo de robot cartesiano juega un papel importante, por lo que la evaluación de la fiabilidad de los controladores es vital, razón por la cual se hace imperioso tener modelos matemáticos sobre los cuales realizar nuevas propuestas de controladores, que garanticen la solución a las mismas con eficiencia en el menor tiempo posible.
Los controladores del robot son aquellos que hacen posible la interpretación de la matemática y que se genere el movimiento de acuerdo con lo planteado analíticamente. El control en el espacio articular requiere la solución de la cinemática inversa del robot para obtener el vector de posición articular partiendo de conocer la trayectoria deseada en el espacio cartesiano del elemento terminal del robot (Urquijo et al., 2017).
Entre las experiencias estudiadas de la literatura científica se encuentra la investigación de Zachi et al. (2006) quienes emplean una estrategia de control adaptativo para manipuladores robóticos. Usando una cámara fija, el movimiento cartesiano 3D se descompone en un movimiento 2D en un plano ortogonal al eje óptico y un movimiento 1D paralelo a este eje. Debido a la falta de calibración de la cámara, se utiliza un método de control adaptativo para garantizar tanto la profundidad como el seguimiento planar en el fotograma de la imagen. El bucle de realimentación de profundidad se cierra midiendo el área de imagen de un objeto fijado al efector final del robot. El esquema empleado proporciona un seguimiento Cartesiano 3D estable sin necesidad de medir la profundidad.
Por otra parte, Rodríguez et al. (2009) presentaron un trabajo sobre control óptimo en línea para tareas de seguimiento de trayectoria en un robot planar de dos grados de libertad. Los autores proponen la combinación de dos estrategias de control implementadas en espacio articular a través del Jacobiano del manipulador: un control Integral-Proporcional-Derivado (PID) Cartesiano para fines de estabilidad y un control optimizante basado en el flujo gradiente para mejorar el desempeño en seguimiento. Un controlador PID se basa en la combinación de 3 acciones proporcional, integral y derivativa, de tal forma que se logren características dinámicas estables en la variable que se requiera controlar.
Para el diseño de ambos controles no se requirió del modelo cinemático inverso del robot. Los resultados experimentales obtenidos evidenciaron un mejor desempeño del lazo cerrado con el control optimizante que solamente con el control PID Cartesiano, lo que implica que ambos controladores se complementan mutuamente para disminuir los errores de seguimiento cartesiano (Rodríguez et al., 2009).
Destaca también el trabajo de Urquijo et al. (2017) quienes implementaron un esquema de control para un robot paralelo neumático de dos grados de libertad en aplicación industrial de simulador de movimiento con el objetivo de resolver el problema de seguimiento de trayectoria. El sistema de control considera dos lazos en cascada; mediante un lazo interno desacoplado se resuelve el control de posición articular, mientras que un lazo externo implementado en el espacio cartesiano elimina los errores cartesianos en el espacio de tareas. Los resultados experimentales evidencian que el esquema propuesto de control de trayectoria en espacio de tareas logra disminuir el error en seguimiento de trayectoria, para la aplicación de simulador de movimiento industrial.
Otro campo de estudio es la robótica colaborativa. En este se puede encontrar el trabajo de Buitrago y Ramos (2016) quienes incursionaron en el empleo de sistemas teleoperados. En estos sistemas existen dos estaciones de trabajo: la maestra y la esclava. El dispositivo robótico llamado sistema esclavo se controla remotamente por un usuario ubicado en un lugar distinto, a través de un mecanismo denominado sistema maestro, para ello usan mecanismos que captan los movimientos del operario, para posteriormente procesar dicha información y convertirla en una serie de comandos interpretados por el robot.
Los autores presentaron una interfaz para controlar de forma remota, dos manipuladores industriales ubicados en celdas de trabajo contiguas, usando el cuerpo humano como un marcador visual de movimiento. Para ello emplearon un Kinect colocado en la estación maestro, que capta al usuario esqueléticamente, para luego, usando el modelo cinemático de los robots y sistemas de control para amortiguar el desplazamiento de ellos, realizar una trayectoria similar a la descrita con las manos. Plantearon un controlador PI para disminuir los errores presentes entre las matrices de transformación homogénea, amortiguar los sobre impulsos producidos por los movimientos inapropiados de los robots y reducir los retardos originados por la comunicación del sistema maestro-esclavo y el procesamiento de la información del Kinect. La aplicación del controlador PI, sintonizado por el método de Ziegler-Nichols, mostró una mejoría significativa en la suavización de las trayectorias, eliminando la mayoría de los sobre impulsos producidos por el ruido en la extracción de la información del Kinect y la sensibilidad del dispositivo para captar los movimientos (Buitrago y Ramos, 2016).
También en esta área Pérez (2022) concibieron el traspaso de una herramienta entre robots colaborativos con sensores de fuerzas en las articulaciones. Para optimizar la ejecución de la tarea plantean utilizar un controlador de impedancia variable en las articulaciones que permita variar la rigidez del robot con el entorno durante la ejecución de la tarea.
En la presente investigación se analiza la fiabilidad de dos controladores de un prototipo de robot cartesiano de dos grados de libertad para el proceso de la logística de mercadería. El prototipo usado se enmarca en la clasificación de los robots paralelos y su área de trabajo es de dos dimensiones a lo largo de los ejes x, y. Se parte de la necesidad del empleo de dos controladores para que en caso de que el controlador principal falle, el otro controlador pueda tomar el control del prototipo lo más rápido posible y completar la trayectoria prevista.
En diferentes ocasiones, las variables de estudio de estos prototipos tienen comportamientos estocásticos, por lo que no se puede realizar un análisis matemático determinístico para caracterizar el comportamiento y la fiabilidad de dichas variables; en este sentido, se requiere emplear métodos probabilísticos para analizarlas, siendo uno de ellos la implementación de la función de densidad no paramétrica, herramienta muy utilizada en el campo de la estadística, puesto que, además de encontrar la media y o la varianza de un conjunto de datos, permite determinar la probabilidad de la variable aleatoria o estocástica de estudio. Una forma de hallar una estimación no paramétrica es el método de estimación de densidad de kernel (KDE por sus siglas en inglés) y la aplicabilidad es amplia en los casos donde la incertidumbre se encuentra presente.
La confiabilidad de los controladores se analiza a través de una función de densidad que caracteriza el comportamiento de los tiempos requeridos para la reconfiguración. La variable de interés es el tiempo que tardan los controladores en reconfigurarse, razón por la cual la obtención de datos es de vital importancia.
El proceso para determinar la mejor estimación de la función de densidad que caracterizará el comportamiento de los tiempos de reconfiguración, se basa en el análisis de estimaciones no paramétricas, específicamente el método de estimación por kernelo núcleo (KDE).
El análisis de datos se realizó con ayuda del software Matlab (Matrix Laboratory). La ventaja de utilizar software al implementar la solución es la automatización de los algoritmos, lo que facilita el análisis para cualquier muestra escogida y garantiza la fiabilidad de los resultados, puesto que todos los parámetros necesarios para la estimación se recalculan sin la necesidad de realizar cambios por el investigador.
Método
El prototipo utilizado como caso de estudio es un robot cartesiano de dos grados de libertad. Tiene una estructura física de 4 eslabones conectados por tres articulaciones y dos servomotores como elementos de accionamiento. La figura 1 muestra el prototipo construido.
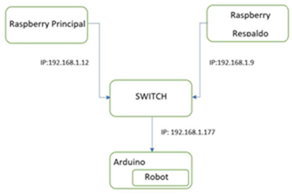
El control cinemático inverso se ha implementado en dos ordenadores de bolsillo, Raspberry Pi3, que vienen equipados con un procesador ARM y están conectados en una red Ethernet con el Arduino Mega 2560, con la ayuda del escudo Ethernet W5100. El Arduino sirve como interfaz entre la Raspberry Piylos servomotores. La figura 2 muestra el esquema de interconexión de los dispositivos.
La información en el agente principal se envía a la red, para detectar si existe un controlador de respaldo, de así ser el controlador de respaldo se provee de toda la información ingresada y a su vez realiza el monitoreo de cada uno de los pasos seguidos por el controlador principal.
El proceso de reconfiguración se lleva a cabo entre las dos Raspberry: el controlador principal y el respaldo. Se implementaron algoritmos capaces de establecer la comunicación y la supervisión del estado en el que se encuentra la resolución de la trayectoria preestablecida, por lo que, si en algún momento llegase a sufrir un desperfecto el controlador principal, el controlador de respaldo habrá recibido la alerta de dicho desperfecto y retomará el control del prototipo con la finalidad de concluir con la trayectoria en curso.
El proceso de adquisición de los datos es de vital importancia en esta investigación y de la calidad de los datos dependerá el análisis de la función de densidad no paramétrica. Los datos que se recolectan para estudiar la función de distribución no paramétrica son los tiempos de reconfiguración que invierten los controladores para resolver la trayectoria planteada en la resolución de la cinemática inversa.
En el controlador secundario se implementó un código de supervisión del proceso de modo que se capaz de determinar el momento exacto en el que el controlador principal ha sufrido un desperfecto, dando inicio al cronometro del reloj interno del controlador, el mismo que se detiene cuando el controlador secundario ha tomado el control del proceso, y de esta forma es como se recolecta los tiempos de reconfiguración.
La población de datos a recolectar es infinita, por lo que se necesita una muestra representativa que brinde la información necesaria para estimar la función de densidad y analizar la confiabilidad. El método utilizado es el muestreo para poblaciones infinitas, según la ecuación 1
(1)
Donde:
z |
es la desviación estándar que para un 95% de confianza, su valor es de 1.96 |
p |
es la probabilidad de acierto, en este caso, es de 0.5 |
q |
es la probabilidad de fracaso y es de 0.5 |
e |
es el error permitido cuyos valores de 5% |
El tamaño de la muestra calculado es de 384datos. El prototipo de robot planar es capaz de resolver trayectorias en dos dimensiones por lo que se planearon trayectorias que se encuentran dentro del área de trabajo permitido. En cada trayectoria planificada se generó el mismo fallo, el cual consistía en desconectar el controlador principal y obtener el tiempo estimado de reconfiguración.
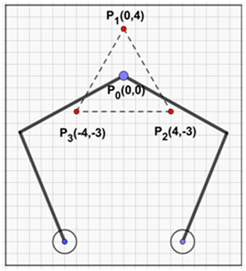
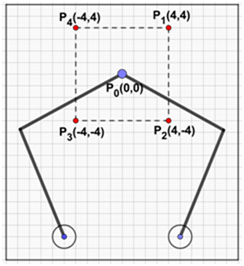
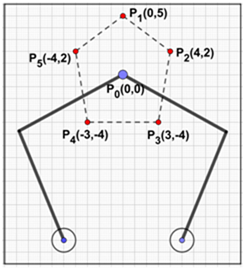
El número de muestras fue obtenido de tres trayectorias fijas (Figuras 3, 4 y 5) y una aleatoria, a las que se les generó el mismo fallo, el cual consistió en terminar la ejecución del algoritmo de resolución de la trayectoria para medir el tiempo de reconfiguración empleado por los controladores. Por cada trayectoria se obtuvieron 100 datos de tiempos de reconfiguración, que en total da 400muestras, pese a que ya se tenía el valor de 384 muestras requeridas.
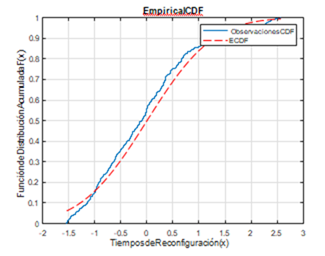
Los datos recopilados se evalúan mediante la prueba de bondad de ajuste de Kolmogorov-Smirnov (Figura 6). Esta prueba supone que está presente una función de distribución específica F0(x), la función de distribución normal. Además, verifica si las muestras obtenidas se distribuyen normalmente.
Seplantealahipótesish 0: F (x) = F 0(x).
El módulo estadístico de Matlab facilita las funciones necesarias para realizar esta prueba con facilidad. Los valores obtenidos fueron: h= 1, p= 0.0249, k=0.0737 y c = 0.0676. Sí k<c se acepta la hipótesis nula, por lo que se concluye que se rechaza la hipótesis nula, de modo que la prueba determina que los datos no se distribuyen normalmente.
La prueba para determinar si los datos de la población provienen de una misma distribución es la de Kruskal-Wallis (Berenson et al., 2006). La prueba se realiza en Matlab. La tabla 1 evidencia los resultados de la prueba. El valor de p es igual a2x10 −10 lo que lleva a concluir que los datos de cada trayectoria provienen de distribuciones diferentes. La prueba implica que se debe estimar la función de densidad para cada uno de los grupos (Figura 7).
Tabla 1 - Prueba de Kruskal-Wallis
| Source | SS | df | MS | Chi-sq | Prob>Chi-sq |
|---|---|---|---|---|---|
| Group | 631402 |
3 | 210467 |
47 |
2 |
| Error | 4661984 |
395 | 11802 |
||
| Total | 5293387 | 398 |
Fuente: Los autores
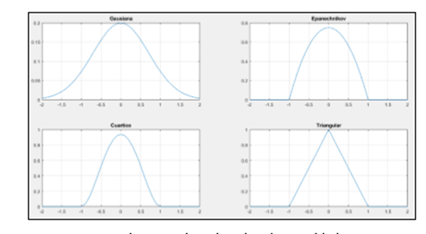
La estimación de la función de densidad es de tipo no paramétrico, como ya se mostró con la prueba de Kolmogorov-Smirnov, puesto que los datos no se distribuyen de forma normal, y es así como se emplea el método en kernel o núcleo, en ese sentido se pretende estudiar los núcleos más importantes con la finalidad de lograr la mejor estimación del comportamiento de los tiempos de reconfiguración de los controladores. La estimación de la función de densidad se desarrolló para cada trayectoria y con cuatro núcleos.
Para estimar la función de densidad no paramétrica existen varios métodos como: el histograma, que necesita un punto inicial x 0, así como el ancho del contenedor h, de tal manera se puede establecer el número de intervalos como:
[x 0+mh,x 0+(m+1)h),con m=± 1, ± 2, ± 3…± ny sean X 1 ,X 2 ,X 3 ,...,X n las muestras independientes.
El estimador de densidad simple puede pensarse como el límite de un histograma de los contenedores cuyo centro se encuentra en x, haciendo que h, el ancho del contenedor tienda a cero, se puede estimar P(x h<X<x+h) por la proporción de la muestra que cae en el intervalo (xh< X < x + h), y el estimador por kernel o núcleo, que emplea una función k llamado núcleo, que encontrará una función fˆ(x) que se aproxime a la función original f(x). Para llevar a cabo este cometido a cada i-ésimo punto de la muestra Xi se asigna una función k, como se muestra en la ecuación 2.
(2)
La función de densidad estimada depende de la cantidad de núcleos escogidos, así como del parámetro de suavizado. La selección del núcleo adecuado juega un papel importante ya que de este depende la mejor estimación de la función de densidad, por lo que se han evaluado los núcleos más importantes (Figura 8). Los núcleos necesitan de un parámetro de suavizado; para ello el método utilizado es el propuesto por Silverman (1998): ecuación 3
(3)
La mejor estimación se evalúa con el criterio del error cuadrático medio (MSE por sus siglas en inglés), porque permite establecer la diferencia entre la función real y la función estimada. El MSE se determina como la suma de la varianza más el cuadrado del sesgo (Durá, 2017) como se muestra a continuación: ecuación 4.
(4)
Resultados
Para llevar a cabo la estimación de la función de densidad no paramétrica de los tiempos de reconfiguración de los controladores del robot planar, se realizó la implementación de un código capaz de detectar y contabilizar la cantidad de tiempo invertido en el proceso de reconfiguración con la finalidad de resolver la trayectoria planificada en la resolución de la cinemática inversa, tiempos que han sido evaluados bajo diferentes kernels o núcleos.
Para poder estimar la mejor función de densidad no paramétrica se evaluaron todas las muestras de los tiempos de reconfiguración recolectados, bajo los criterios de los kernels o núcleos seleccionados.
En la estimación de la función de densidad, el estimador para la selección del mejor modelo es el error cuadrático medio. En la Tabla 2 se evidencia el error cuadrático medio obtenido por trayectoria y por núcleo. El menor MSE hallado se da con la evaluación de núcleo normal o gaussiano.
Tabla 2 - Error Cuadrático Medio (MSE)
| Trayectoria/ECM | Epanechnikov | Cuártico | Triangular | Gaussiano |
|---|---|---|---|---|
| Trayectoria 1 | 4,2507 | 4,3772 | 4,3477 | 2,9085 |
| Trayectoria 2 | 5,0406 | 5,1285 | 4,9682 | 3,4843 |
| Trayectoria 3 | 3,4186 | 3,4295 | 3,4604 | 2,3345 |
| Trayectoria 4 | 6,1574 | 5,7084 | 4,8972 | 2,4749 |
Fuente: Los autores
De acuerdo con los resultados obtenidos el menor MSE hallado se da con la evaluación de núcleo normal o gaussiano, por lo que se concluye que este núcleo es el que determina el mejor comportamiento de los tiempos de reconfiguración del prototipo de un brazo robótico planar.
En los procesos de transporte y manipulación de mercancías, la fiabilidad del prototipo de robot cartesiano juega un papel importante, por lo que la evaluación de la fiabilidad de los controladores es vital. La confiabilidad es la capacidad de un producto o sistema para realizar las funciones requeridas en condiciones establecidas durante un período específico. La confiabilidad es un factor clave en el diseño de sistemas que deben realizar las funciones requeridas en condiciones que con frecuencia no son las ideales, como durante un corte de energía o una caída del sistema.
Gracias a la disponibilidad de la función de densidad se puede obtener la función de distribución y la función de fiabilidad. Para ello basta con obtener la diferencia entre la unidad y la función de distribución. La fiabilidad obtenida al 95% de confianza para cada una de las trayectorias se detalla en la Tabla 3. La confiabilidad de los controladores caracteriza el comportamiento de los tiempos requeridos para la reconfiguración.
Tabla 3 - Fiabilidad al 95% por trayectoria y núcleo
| Trayectoria/ECM | Epanechnikov | Cuártico | Triangular | Gaussiano |
|---|---|---|---|---|
| Trayectoria 1 | 1.005s | 1.056s | 0.9987s | 1.036s |
| Trayectoria 2 | 0.9695s | 0.9645s | 0.9576s | 0.9601s |
| Trayectoria 3 | 0.9776s | 0.9711s | 0.9672s | 0.9729s |
| Trayectoria 4 | 1.009s | 1.002s | 1.003s | 1.002s |
Fuente: Los autores
La función de densidad que representa el comportamiento de los datos está dada por la ecuación 5.
(5)
Dónde 𝑛 es el número de muestras por trayectoria y ℎ el ancho de banda determinado por el método de Silverman.
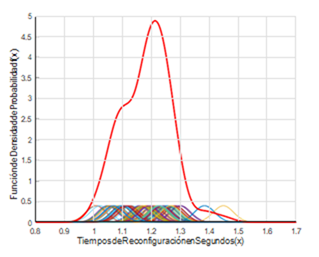
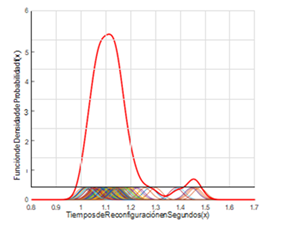
La evaluación de la función genera una curva por cada una de las trayectorias planificadas. Las curvas de las figuras 9, 10 y 11 representan a las trayectorias fijas, mientras que, la trayectoria aleatoria se visualiza en la curva de la figura 12.
La trayectoria 1 está formada por tres puntos y se han tomado cien datos como muestra, donde se obtiene un tiempo medio de reconfiguración de: 1.1814 segundos y se estimó la función de densidad con núcleo normal obteniendo un error cuadrático medio de: 2.9172%.
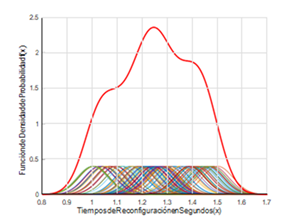
La trayectoria 2 está formada por cuatro puntos que, a su vez, tiene tomado cien datos como muestra, donde se obtiene un tiempo medio de reconfiguración de: 1.1329 segundos y se estimó la función de densidad con núcleo normal obteniendo un error cuadrático medio de: 3.4667%.
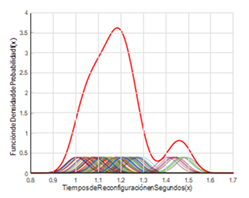
La trayectoria 3 está formada por cinco puntos que, a su vez, tiene tomado cien datos como muestra, donde se obtiene un tiempo medio de reconfiguración de: 1.1805 segundos y se estimó la función de densidad con núcleo normal obteniendo un error cuadrático medio de: 2.3160%.
La trayectoria 4 como tal no es fija, sino que aquí se generaban trayectorias aleatorias tomando así cien datos como muestra, donde el tiempo medio de reconfiguración de: 1.2488 segundos y la función de densidad con núcleo normal obteniendo un error cuadrático medio de: 2.4749%
Conclusiones
En las últimas décadas se ha intensificado la investigación e inversión en el área de la robótica aplicada a la industria. La utilización de robots se justifica por una reducción de costes y por su mayor rendimiento en ciertas tareas repetitivas o de alta precisión. Su propósito es el de ayudar a mejorar las condiciones de vida del ser humano.
El empleo de la robótica implica la necesidad de utilizar mecanismos controladores que aseguren la fiabilidad del robot. En los procesos de transporte y manipulación de mercancías, la fiabilidad del prototipo de robot cartesiano juega un papel importante, por lo que la evaluación de lafiabilidad de los controladores es vital, razón por la cual se hace imperioso tener modelos matemáticos sobre los cuales realizar nuevas propuestas de controladores, que garanticen la solución a las mismas con eficiencia en el menor tiempo posible.
Los tiempos que tardan los controladores en reconfigurarse dependen de la trayectoria diseñada que se está ejecutando. La trayectoria implementada para la resolución de cinemática inversa impacta directamente en la confiabilidad de los controladores. La estimación de densidad no paramétrica con kernel normal determina el mejor comportamiento de los tiempos de reconfiguración del prototipo de un brazo robótico planar.
La principal contribución de este trabajo fue la aplicación del enfoque de función de estimación de densidad del núcleo (KDE) para validar prototipos en desarrollo y análisis de fiabilidad.