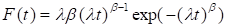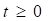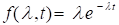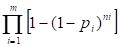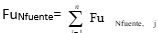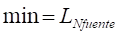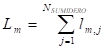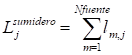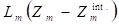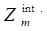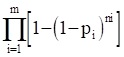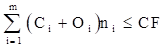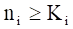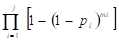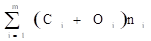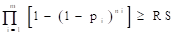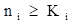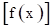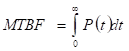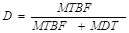Introducción
Los procesos químicos son un campo de la aplicación de la integración material y energética porque un alto número de corrientes materiales y energéticas están involucradas a diferentes niveles de temperatura y concentración de materiales utilizables. Esto permiten al diseñador considerar modificaciones de procesos que propician una buena integración material y de energía, con vista a obtener mayores beneficios técnicos económicos y ambientales con objetivo el objetivo final de mejor compensación entre los costos de operación y complejidad de la planta (Morandin, 2011).
En la literatura se han reflejado los procedimientos para la consideración de la incertidumbre (Concepción et al, 2021) (Valdés et al., 2020) y como se ha dicho, (Bacci & Chiandotto, 2020), un aspecto relevante que el decisor debe considerar es el nivel de conocimiento sobre los procesos reales.
En la literatura científica se reflejan se reflejan varias investigaciones sobre la integración de procesos como el de uso y minimización de residuos acuosos (Dunn, 2003), referido al uso de la energía en los procesos que de etanol en la etapa enzimática (Palacios-Bereche et al., 2011) sobre integración de producciones de etanol de primera y segunda generación de Palacios-Bereche et al.( 2013), sobre integración de diferentes instalaciones de producción de etanol y azúcar (Pina et al., 2014), sobre la integración en columnas de destilación con restricciones técnicas y económicas (Ulyev et al., 2018), e integración de calor en una instalación industria redes de calor de Ulyev & Kanischev (2021), integración de una refinería (Bonachea et al, 2021).
Es por ello que se aborda un conjunto de procedimientos metodológicos que viabilicen el desarrollo del análisis de factibilidad técnica y económica de la integración de procesos en la industria química y fermentativa, considerando la incertidumbre asociada a la fiabilidad de las plantas y a los balances de masa y energía en las mismas.
Materiales y métodos
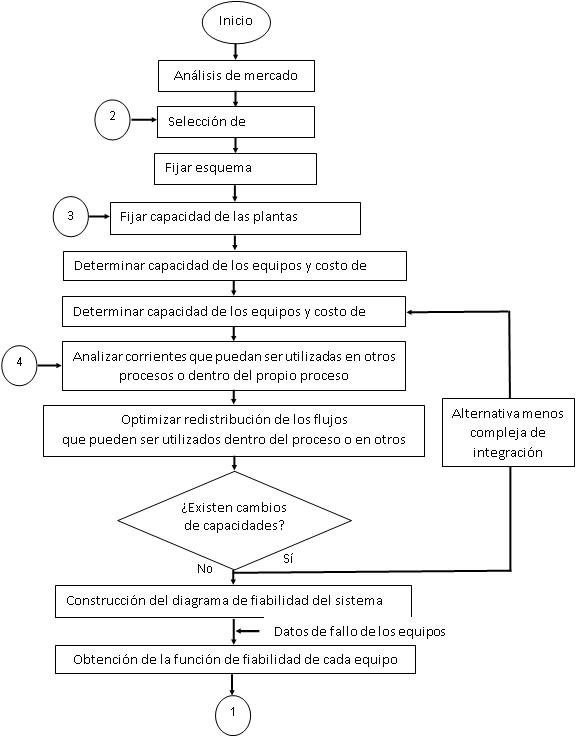
Esta metodología está conformada por un procedimiento heurístico general, esbozado en la figura 1, complementándose con otros que abordan, la integración de procesos y la optimización de las corrientes intercambiadas, el maximizar la fiabilidad del complejo integrado y realizar la evaluación económica, teniendo en cuenta, el impacto de la consideración de la incertidumbre en los balances de masa y energía.
El diagrama heurístico comienza con el análisis de mercado, el cual tiene como objetivo determinar la cantidad de bienes y servicios provenientes de la unidad de producción en estudio. Este en la etapa de preinversión debe considerar aspectos relacionados con la oferta, la demanda, la relación entre oferta y demanda, los precios etc.
Este análisis debe realizarse de forma profunda y con la conjugación de métodos económicos y matemáticos, no se considera dentro de los objetivos del trabajo por lo que en el mismo se parte de que este estudio fue realizado anteriormente.
Después debe seleccionarse la tecnología, con lo que debe lograrse la selección de la mejor opción, técnica, económica y ambiental para la transformación de las materias primas e insumos en los productos. Esto permite fijar el esquema tecnológico, aspecto importante cuando se requiere diseñar de una planta.
El siguiente paso es fijar la capacidad de la planta, apoyándose en la macrolocalización de la misma teniendo en cuenta la incertidumbre en la demanda del producto o en la disponibilidad de la materia prima. Luego a partir de los balances de masa y energía se calcula la capacidad de los equipos y se determina el precio de adquisición de los mismos.
 Fuente: elaboración propia.
Fuente: elaboración propia.Fig. 1 - Diagrama heurístico para la consideración de la incertidumbre en la industria química y fermentativa
Este paso es de gran importancia pues permite obtener las cotas mínimas de cada uno de los equipos, esto significa la cantidad mínima de equipos que deben operar para que se garantice la capacidad de la futura instalación, además de las capacidades de almacenamiento intermedio.
A partir de aquí la metodología transita por tres etapas fundamentales, interrelacionadas de modo tal que facilitan el análisis de múltiples alternativas; que consideren:
Integración material y energética de los procesos involucrados
Análisis de disponibilidad de los equipos en el complejo integrado
Impacto de la incertidumbre en los balances de masa y energía en el análisis inversionista
Dentro de la integración de procesos juega un papel fundamental la búsqueda de oportunidades para la mejor distribución de la energía en el proceso. Entre los métodos de integración de procesos que han sido desarrollados con este fin la tecnología Pinch es el más usado. Son numerosos los ejemplos en los que por el uso de la tecnología Pinch se ha logrado un ahorro del consumo energético en rangos del 10-30% y en la mayoría de los casos ha sido necesario invertir en pequeños capitales para implementar las soluciones propuestas (Catá, 2006)(Fodor et al., 2012), afirman que el análisis mediante el uso tecnología Pinch, debido a su simplicidad se usa ampliamente para determinar el consumo de energía, diseñar la red de intercambio de calor e identificar las oportunidades para la integración de procesos. Cuando la integración de procesos se combina con otras herramientas es un enfoque poderoso que permite a los ingenieros analizar sistemáticamente los procesos industriales y la interacción entre sus partes.
Por otra parte, en el caso de la integración material en las plantas, con vista a minimizar el consumo de agua fresca, se puede emplear la herramienta de bajo costo el diagrama fuente sumidero. Dunn, (2003), tambien Tong et al, (2016) han utilizado herramientas de bajos costo con este fin, logrando reducir el consumo de agua fresca en algunos casos hasta un 85 %. Esta es una herramienta gráfica que permite identificar las posibilidades de mezclado, reciclo directo y las necesidades de intersección de flujos, por lo que se requiere obtener la redistribución óptima de los flujos a partir de un tratamiento matemático.
Para el análisis de fiabilidad de las plantas se necesita realizar un estudio de los fallos de los equipos. Si las plantas se encuentran funcionando, se toma el historial de fallo de sus equipos y en el diseño de nuevas plantas, es factible emplear la información obtenida de los equipos instalados en otras industrias con condiciones similares a las de instalación que se proyecta (Concepción et al, 2021).
Con los datos de fallos de los equipos se realizó el estudio para determinar las funciones de distribución para cada equipo en condiciones determinadas. En Fiabilidad, la distribución de referencia es la Exponencial. Las buenas propiedades de esta distribución, consecuencia de su ausencia de memoria, permiten simplificar los problemas de inferencia; por el mismo motivo su aplicación práctica es limitada, siendo más utilizadas generalizaciones suyas, como las distribuciones Weibull o Gamma), en el caso de las plantas estudiadas las distribuciones más usadas fueron la exponencial y la de Weibull, esto no quita que se obtuvieron otras distribuciones.
La distribución de Weibull se define como (ecuación 1):
donde los parámetros 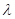 y
y 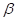 denominados factor de forma y de escala respectivamente toman valores positivos. Esta función es siempre monótona; es creciente si
denominados factor de forma y de escala respectivamente toman valores positivos. Esta función es siempre monótona; es creciente si 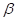 > 1 y decreciente si
> 1 y decreciente si 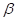 < 1. Si
< 1. Si 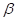 = 1, la función de riesgo es constante y corresponde al modelo Exponencial. Lo anterior demuestra que el modelo exponencial es un caso particular del modelo de Weibull.
= 1, la función de riesgo es constante y corresponde al modelo Exponencial. Lo anterior demuestra que el modelo exponencial es un caso particular del modelo de Weibull.
El tratamiento matemático de la distribución exponencial es sencillo. Matemáticamente se expresa por (ecuación 2):
((0, t(0 (2)
El parámetro ( se le llama comúnmente razón de fallos.
Para la obtención de la función de fiabilidad se debe confeccionar previamente el diagrama correspondiente tanto para cada planta, como para el complejo integrado. El tipo de diagrama más recomendado es el siguiente:
La función de fiabilidad resultante se obtiene mediante la combinación de ecuaciones siendo (ecuacion 3):
(3)
Donde:
ni - |
Número de equipos que deben colocarse en cada módulo o planta |
pi - |
Fiabilidad de cada tipo de equipo o planta. |
Esta ecuación se pudo utilizar tanto para una planta o para un complejo integrado.
La formulación del modelo matemático para la obtención de la fiabilidad del sistema se basa en las combinaciones de costo y fiabilidad de los equipos según lo planteado en el capítulo anterior. Al modelo se le incorporan los resultados de los balances de materiales y energía que aportan la cota mínima de cada uno de los elementos del sistema.
Como resultado de la optimización se obtiene el número óptimo de equipos en cada una de las etapas y la fiabilidad de las plantas, sustituyendo los valores óptimos obtenidos en la ecuación de fiabilidad que está en función de los mismos; posteriormente se calcula el tiempo medio entre fallos y la disponibilidad de las plantas. Al tener la fiabilidad óptima de las plantas se realizó el mismo análisis, pero en este caso, para el complejo integrado, calculando el tiempo medio de trabajo sin fallo y la disponibilidad del sistema, sin la cual no es posible calcular el verdadero valor de los ingresos anuales. Las valoraciones económicas del trabajo de fiabilidad pueden calcularse mediante las categorías económicas de costo de inversión, costo de operación y costo a causa de los fallos.
A este análisis económico se debe añadir los aspectos relacionados con la consideración de la incertidumbre en los balances de masa y energía por estar estrechamente vinculada tanto al dimensionamiento de los equipos en el diseño como a la demanda de los productos, haciéndose necesario tomar información de los procesos, lo que disminuye los riesgos en el análisis inversionista (Nápoles, 2004).
Se analizó la influencia de la incertidumbre de las mediciones en los balances de masa y energía, se requiere evaluar cómo afectan los errores de las mediciones en las diferentes plantas de cualquier industria, y bajo qué condiciones se deben diseñar las nuevas plantas. Considerando los resultados de la integración y la fiabilidad de los equipos se realiza el estudio de la incertidumbre en los balances de masa y energía de forma integrada.
Posteriormente debe realizarse un análisis de sensibilidad univariable y multivariable, para la selección de las variables que más afectan en las salidas o respuestas de los balances de masa y energía, que constituyen en muchos casos, las materias primas de las plantas involucradas en el complejo fabril analizado, y con esto se estima la incertidumbre en las variables de salidas y a los indicadores económicos.
Será seleccionada en el análisis comparativo, aquella alternativa que presente los resultados económicos más atractivos, ya que se considera que todas las alternativas planteadas son optimizadas desde el punto de vista tecnológico. Los métodos dinámicos de análisis de inversiones que deben ser utilizados son: el VAN, la TIR, y el PRD.
Resultados-discusion
Integración material y energética de los procesos involucrados.
Para llevar a cabo la integración de procesos en un complejo integrado, se recomienda tener en cuenta el principal objetivo propuesto y así decidir, que será lo más factible. Sí comenzar con el análisis energético y luego continuar con la minimización de residuales ó viceversa, siempre teniendo en cuenta que se debe realizar en las plantas por separado y luego analizar el impacto de las soluciones en el complejo fabril.
Un ejemplo puede ser determinar el consumo mínimo de utilidades frías y calientes en las plantas, utilizándose el análisis Pinch para obtener la redistribución óptima de los flujos.
Realizándose el siguiente análisis: el proceso tiene Nsumideros, que son los equipos o etapas que tienen requerimientos de utilidades calientes o frías, y tiene Nfuentes, flujos con calidad térmica que pueden ser utilizados para suplir el requerimiento de las utilidades. Entre los flujos fuentes, se encuentra el flujo de vapor que se genera en las fábricas, en este caso es éste el flujo que se quiere minimizar. Por tanto, si se nombra como la Nfuente el flujo de vapor que se genera en las calderas y que se utiliza para el calentamiento de corrientes en cada proceso, la función a minimizar será (ecuación 4):
(4)
donde: FuNfuente: flujo de utilidades de la Nfuente, n: número de fuentes, j: sumideros. Sujeta a las restricciones del balance energético.
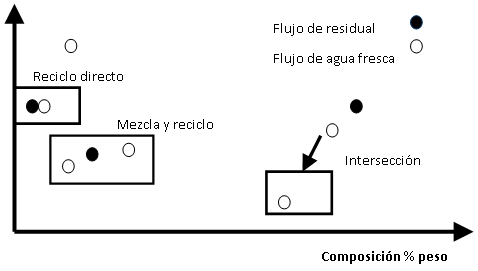
Se puede plantear como uno de los objetivos de esta etapa, disminuir el consumo de agua fresca a través del reciclo de los efluentes generados durante los procesos, utilizando el diagrama fuente-sumidero para identificar las posibles soluciones, en la figura 3 aparece una representación de las herramientas con las posibles soluciones iniciales que se pueden obtener las cuales son explicadas a continuación.
 Fuente: elaboración propia.
Fuente: elaboración propia.Fig. 3 - Representación gráfica del diagrama fuente- sumidero y las posibles soluciones.
Segregación: separación de fuentes en el proceso. En muchos procesos, hay una mezcla innecesaria de flujos que conducen a la dilución. La segregación de estas fuentes resulta en altas concentraciones de la especie de interés y consecuentemente más fácil separación además de potencialmente menores costos de tratamiento.
Mezcla: debe llevarse a cabo cuando, para dar una fuente de cierta composición y relación de flujo, dos o más fuentes con diferentes composiciones y relaciones de flujo son mezcladas en proporciones adecuadas, esto puede determinarse a través de un balance de masa. Si se quieren satisfacer los requerimientos de composición y relación de flujo de cierto sumidero, el mezclado de diferentes fuentes puede ser llevado a cabo en proporciones adecuadas.
Reciclo o reuso: ocurre cuando cierta fuente en el proceso, con composición y relación de flujo que hace juego con el flujo que será usado por cierto sumidero, puede entonces utilizarse el reciclo en lugar de éste. Esto se conoce como reciclo directo.
Intersección: La intersección se refiere a la separación de la especie de interés desde una fuente objetivo. Puede ser usada para disminuir la masa de la especie en una fuente dada. Esto se hace en aquellos casos en los que es necesario disminuir la carga de contaminantes, para poder reciclar la corriente a algún equipo.
Esta herramienta siempre debe acompañarse de una estrategia de optimización, al existir diversas variantes de solución a partir del análisis gráfico. Planteándose la estrategia matemática con vista obtener la redistribución óptima de los flujos dentro de los procesos. Si se tiene en cuenta que el proceso tiene Nsumideros y Nfuentes y los Nsumideros se corresponden con el número de unidades que requieren agua fresca como entrada y en las fuentes (corrientes que llevan la especie de interés) se considerará sólo una fuente de agua fresca, siendo (Nfuente-1) flujos de efluentes acuosos que pueden ser potencialmente reciclados.
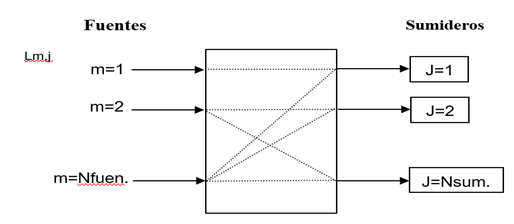
Representando el problema como aparece en la figura 4, puede plantearse la función objetivo y las restricciones. La solución debe converger a lograr el objetivo principal, minimizar el consumo de agua a través del reciclo de los efluentes.
 Fuente: elaboración propia.
Fuente: elaboración propia. Fig. 4 - Representación de la distribución de flujos desde las fuentes a los sumideros para la formulación matemática del problema.
Función objetivo:
donde: 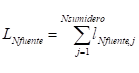 j = 1,2…..Nsumidero (5)
j = 1,2…..Nsumidero (5)
Sujeta a las restricciones de segregación, reciclo e intersección que se muestran a continuación:
m = 1,2..... Nsumidero (6)
donde: Lm = flujo total de la fuente (m)
j = 1,2..... Nsumidero (7)
donde: l m,j = flujo individual que pasa de una fuente (m) a un sumidero (j)
j = 1,2..... Nsumidero (8)
donde: 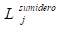 =flujo total que entra al sumidero(j),
=flujo total que entra al sumidero(j),
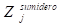 = composición de entrada al sumidero(j)
= composición de entrada al sumidero(j)
=masa removida m = 1,2..... Nfuente (9)
donde:
es la composición de la especie de interés en la fuente (m) después de la intersección |
|
composición de la fuente (m). |
En el modelo, pueden plantearse otras restricciones como son las de no-negatividad, la cual garantiza que no se obtengan valores negativos de flujo y composición, y en este caso además se plantearon restricciones para que no se reciclaran residuales a los sumideros que previamente se decidió utilizarían agua fresca
Las soluciones encontradas a través de la utilización de las herramientas de integración de procesos, por muy pocos cambios que se ejecuten en las plantas para lograr los objetivos planteados, traen consigo un aumento de la complejidad de los sistemas.
Lo anterior ha propiciado la inclusión de los estudios de fiabilidad en el análisis de alternativas de inversión, para dar respuesta a una de las barreras de la integración de procesos: el hecho de que una planta o parte de la misma salga de funcionamiento, lo cual puede estar dado por diversas causas, garantizando que afecte lo menos posible el resto del complejo integrado. De aquí que se trate este aspecto en el próximo epígrafe.
Análisis de disponibilidad de los equipos en el complejo integrado.
Para analizar la disponibilidad a través de los estudios de fiabilidad se comienza por obtener a partir del diagrama de flujo del proceso y del estudio de la interrelación de cada uno de los módulos el diagrama de fiabilidad del sistema, esto es indispensable ya que a partir del mismo se establecerá la función de fiabilidad del sistema necesaria en la formulación del modelo matemático. Con vistas a obtener la probabilidad de trabajo sin fallo de cada uno de los elementos del sistema, se toman los datos de fallos directamente en la industria a partir de datos históricos y se evalúan los mismos según la metodología propuesta. La obtención de los datos de fallos de los equipos se realiza considerando: *I: Artículo considerado, II: Condiciones de trabajo, III: Elemento o pieza que sufre el fallo, IV: Régimen de trabajo diario, V: Fecha de inicio del trabajo, VI: Fecha en que se presenta el fallo, VII: Causa o motivo del fallo, VIII: Tiempo de reparación del fallo, IX: Tiempo de trabajo sin fallo.
Posteriormente se procede al cálculo de la Probabilidad de trabajo sin fallo P(t)i en todas las plantas que integran el complejo. Para el establecimiento del grado de concordancia entre la distribución empírica y teórica se utilizan las pruebas de Kolmogorov- Smirnov según lo planteado en Barlow, (1965).
En la construcción del diagrama de fiabilidad tanto de las plantas como del sistema integrado se deben seguir los siguientes pasos:
Estudiar los diagramas de flujo de los procesos.
Estudiar las interacciones entre los equipos y secciones de cada proceso para determinar si responden a una estructura en serie o en paralelo o una combinación de las mismas. En el caso del complejo integrado se deben analizar las interacciones entre las plantas.
Construir los diagramas de fiabilidad.
Establecer las funciones de fiabilidad.
Como puede verse el objetivo de esta etapa en la metodología es optimizar la fiabilidad del sistema, encontrándose la cantidad de equipos que deben colocarse en cada módulo para que este opere correctamente limitado por el costo de cada equipo (ver figura 5). Por este motivo es importante definir las condiciones límites de redundancias y costos una vez que se ha establecido el objetivo de la optimización. Para lograr el mismo se realiza el siguiente análisis, partiendo de optimizar las plantas por separadas, para luego optimizar el complejo, en el caso de una planta se plantea que está compuesta por m módulos:
Si las variables del sistema son n1, n2, n3,..nm las cuales corresponden a la cantidad de unidades en cada módulo desde i=1 hasta m, y si se conocen las fiabilidades de cada módulo (pi) desde i=1 hasta m, el costo de adquisición (Ci) y operación (Oi) de cada unidad i. Para el cálculo del costo de operación se analiza que en el mismo deben incluirse mantenimiento, depreciación, utilidades y mano de obra, tomándose las consideraciónes planteadas por Peters & Timmerhaus (1981).
Teniendo en cuenta lo anterior se pueden proponer dos problemas, maximizar la fiabilidad del sistema sujeto a restricciones de costo o minimizar el costo sujeto a restricciones de fiabilidad.
Si el objetivo es maximizar la fiabilidad el planteamiento del problema es el siguiente (ecuación 10):
Maximizar
(10)
siendo la función de fiabilidad del sistema.
Sujeto a las restricciones de costo que se expresarán por (ecuación 11):
(11)
Donde Ci es el costo de adquisición, Oi es el costo de Operación y CF es la cantidad de capital disponible para la inversión en cada planta.
Y a las restricciones que provienen del balance de materiales y energía (ecuación 12)
(12)
Siendo Ki es el número de unidades que deben funcionar en cada módulo.
Para el complejo se plantea la misma función objetivo (ecuación 2.10), pero en este caso j será la cantidad de plantas a tener en cuenta y m1, m2, m3,..mj son las variables del sistema que corresponden al número de equipos por plantas, quedando la función objetivo para el complejo integrado de la siguiente forma (ecuación 13):
(13)
Si el objetivo es minimizar el costo entonces el modelo que se obtiene es el siguiente:
Minimizar el costo que viene expresado por (ecuación 14):
(14)
Sujeto a restricciones de Fiabilidad (ecuación 15):
(15)
Y restricciones de número de equipos en cada módulo (ecuación 16):
(16)
La ecuación 13 puede sufrir modificaciones si es necesario considerar los almacenamientos intermedios para aumentar la fiabilidad, sujeta la capacidad de almacenaje, de forma tal que garantice el objetivo propuesto en el problema.
El planteamiento de uno u otro modelo depende de las condiciones específicas del problema a tratar. Para la solución del problema se necesita seleccionar un método de optimización, teniendo en cuenta la forma que tienen la función objetivo y las restricciones del problema, además de la solución que se desea obtener.
En el primer caso se tiene una función objetivo no lineal con restricciones lineales y en el segundo caso se tiene una función objetivo lineal con restricciones lineales y no lineales, la solución en los dos casos tiene que ser entera. Estos problemas con estas características, se pueden solucionar usando la Programación Dinámica y la Programación No Lineal en Enteros
Si nos encontramos en presencia de plantas integradas en un sistema complejo, donde lo que se necesita es obtener la máxima fiabilidad de las mismas y en el complejo fabril, se escoge el primer caso, estando en presencia de un problema de Programación No Lineal en Enteros (PLNE) siendo necesario destacar que la solución de números de equipo debe ser un entero. Pueden surgir dificultades cuando la función objetivo no lineal es compleja o depende de un alto número de variables independientes. Si por otro lado se imponen restricciones en forma de expresiones complejas de varias variables independientes, la solución del problema de optimización se hace más difícil y es necesario utilizar técnicas de cálculo especiales.
Además, si el problema práctico requiere soluciones enteras y no negativas hay que recurrir a algún algoritmo matemático que resuelva esta situación (Rosa, 1996).
El método de PNLE se basa en la optimización de una función objetivo no lineal (ecuación 17):
MAX o MIN
(17)
Sujeto a varias restricciones lineales o no lineales :
A M (m,n) = [aij]i= 1,n
b Em = (b1,b²,...bm)
x En = (x1,x²,...xn).
Por la complejidad que representa el procedimiento matemático para buscar la solución óptima se necesita un software que garantice la obtención de resultados en el más breve plazo.
Los modelos que deben confeccionarse para la utilización del método se corresponden plenamente con los propuestos anteriormente, las funciones y sus restricciones deben ser introducidas en un fichero con extensión gms. Existe una limitante en la versión del GAMS que se posee, ya que el número de variables enteras a dar como repuesta es limitado, por lo que para el análisis del complejo fabril se pueden analizar varias alternativas con vistas a reducir el número de variables para obtener la solución óptima.
Con los resultados obtenidos de la optimización se calcula el valor de la fiabilidad del sistema de acuerdo a la ecuación 2.3, sustituyendo los valores de cada una de las variables por el valor de redundancia óptimo y se procede al cálculo del tiempo medio entre fallos que responde a la siguiente ecuación (ecuación 18):
(18)
Esta integral impropia es convergente, por lo que conociendo el valor de la fiabilidad del sistema y el tiempo para el cual se realiza la evaluación, siendo para este caso de un año, se puede obtener el valor de Tiempo Medio Entre Fallos, conocido también como MTBF. Este valor es el que permite calcular la disponibilidad de la planta utilizando la siguiente expresión (ecuación 19):
(19)
Donde: MDT = Tiempo medio de paradas
Estos pasos anteriores, se recomiendan realizarlos primeramente en cada planta por separado, donde se obtienen los valores de fiabilidad óptima para cada una, y luego se plantear el modelo para el complejo fabril integrado teniendo en cuenta los valores óptimos, obteniéndose el mínimo de variables independientes en la función objetivo del complejo para dar respuesta a la limitante del software.
Impacto de la incertidumbre en los balances de masa y energía en el análisis inversionista.
Para determinar el impacto de la incertidumbre en los balances de masa y energía en el proceso previo inversionista considerando los aspectos antes descritos, se necesita comenzar con un muestreo de la información básica analizando su calidad a través de la estadística descriptiva. Lo anterior se puede realizar mediante mediciones directas, si la instrumentación en general tiene las condiciones adecuadas, o utilizando información histórica reportada de años anteriores.
Se recomienda realizar el muestreo con la combinación de dos métodos: a partir de mediciones directas y en el caso de no ser posible, por las condiciones de instrumentación actual, obtener los datos a partir de la información histórica de las variables. En este último caso se toman las condiciones medias para aquellas variables en las que fue imposible encontrar diferentes valores reportados.
Para descartar las variables de entrada que tienen un efecto superfluo sobre las respuestas seleccionadas en el modelo de medición, es recomendado realizar este análisis en dos etapas: el univariable con la aplicación de la simulación siguiendo un criterio de por ciento de significación en la respuesta y el multivariable, utilizando el diseño factorial completo 2K sin réplicas, con las curvas normales de diagnóstico conjuntamente con un análisis de varianza según (Nápoles, 2004).
Para facilitar el trabajo los balances de masa y energía de las plantas analizadas deben ser montados un software de manera tal que estén vinculadas las variables de salidas de las plantas con el resto de las fábricas en el caso que sean materias primas de estas facilitándose la simulación de los procesos.
A esta programación dinámica, se deben incorporar los procedimientos para la determinación de la incertidumbre en los balances de masa y energía en todas las plantas incluyendo el análisis económico con vistas a determinar la mejor alternativa de diversificación. De esta forma se puede desarrollar un software que permite analizar de forma dinámica diferentes alternativas de inversión, considerando los resultados de la integración de procesos en los balances de masa y energía, la incertidumbre en los propios balances y la fiabilidad de los equipos.
Con las variables involucradas que sean más importantes al tomar los valores históricos se obtienen los resultados de la estadística descriptiva con el Statgraphics. Luego se procede a efectuar cambios de cada una de las variables implicadas en el sistema. Los cambios efectuados a cada variable son de +/- 10 % o menor según las características de esta, pues es necesario respetar los límites muy estrechos que por condiciones tecnológicas, ecológicas o económicas no es posible variar.
Los cambios se realizaron a una variable en cada ocasión, para verificar su influencia aislada en la respuesta. Según los resultados obtenidos se seleccionarán las variables que tengan un efecto en las respuestas, tomándose como criterio que el valor de la salida cambie al menos en un 5 %. Con este conjunto de variables, para las cuales se reportó más de un 5 % de variación en las variables de salida, se tiene un primer tamizado en la selección para estudios de diseño, análisis de influencia de la incertidumbre, de optimización de las condiciones de operación, o de cualquier otro aspecto a valorar. Lo descrito anteriormente se debe hacer en cada planta por separado y luego ir incluyendo las variables de salidas que sean variables de entradas en el resto de las fábricas para determinar la propagación de la incertidumbre a lo largo del complejo y su influencia en el análisis económico.
Luego se procedió a realizar el análisis de sensibilidad multivariable, se calculan los efectos y se construye la curva de diagnóstico de probabilidad normal. Para la construcción de las gráficas de efecto de probabilidad para los experimentos 2K factorial sin réplicas se requiere realizar 4 pasos (Nápoles, 2004):
Calcular los efectos
Construir una gráfica de probabilidad normal de todos los efectos: esta gráfica tiene en el eje de las abscisas una escala según el valor numérico (+) o (-) de los efectos calculados en 1 y en el eje vertical las fracciones fi de los cuartiles;
Los efectos que caen fuera de la línea recta se deben considerar como efectos reales o significativos. Según el tipo de gráfica de probabilidad normal que se construya será la interpretación.
Luego se puede corroborar el resultado realizando un análisis de varianza (ANOVA).
De aquí se extraen los efectos no significativos, así como las interacciones de órdenes superiores (tres en adelante) para llevar a cabo un análisis de varianza. En este caso se analiza la probabilidad asociada a cada uno, las que den mayores que 0,05 serán no significativas. Las variables que cumplan con lo anterior son las que se tendrán en cuenta para determinar la incertidumbre.
Conclusiones
Del análisis de probabilidad del trabajo sin fallo, se pueden sacar conclusiones sobre el sistema de mantenimiento planificado, su efectividad y la posibilidad de recomendar o no un nuevo plan de mantenimiento.
De la estadística descriptiva para las variables respuestas se obtiene la incertidumbre de las mismas, pero al estar presente en este caso varias plantas y con vista a no eliminar escenarios que pudieran resultar interesantes para el análisis económico, se propone determinar además la incertidumbre en los indicadores económicos dinámicos, este último aspecto es tratado posteriormente.
Una vez que se tenga la incertidumbre en cada variable de salida y en los indicadores económicos, es necesario realizar la evaluación económica del proyecto. Si se tiene en cuenta que el futuro u horizonte económico de la inversión difícilmente puede conocerse con precisión, pues una serie de factores o agentes externos incontrolables, ajenos al propio proyecto, condicionan e influyen en los resultados del mismo. El desembolso inicial, los flujos netos de caja e incluso la duración de la inversión, en innumerables casos se comportan de forma aleatoria. En el mundo económico actual, nos movemos casi siempre en el campo de la incertidumbre.
Con los procedimientos descritos anteriormente la aplicación de la metodología para la consideración de la incertidumbre en la integración de procesos en la producción de biocombustibles permite disminuir los riesgos en el proceso inversionista.