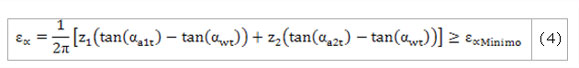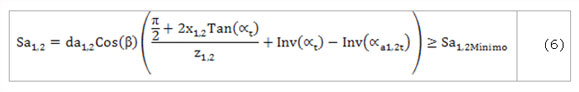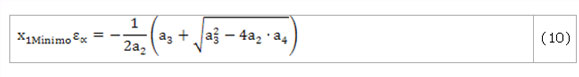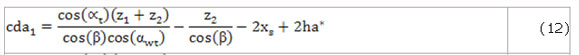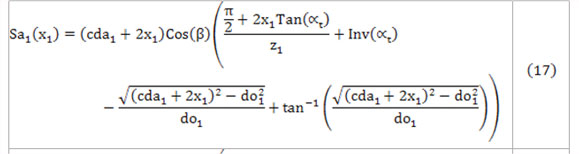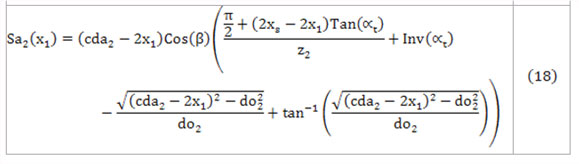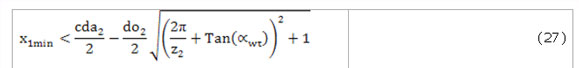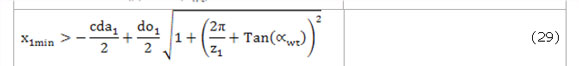ARTICULO

 

Modelo matemático para la utilización analítica del Contorno de Bloqueo en engranajes con dientes asimétricos

 

Mathematical model for The analytical use of Blocking Contour in gears with asymmetric teeth

 

 

Robert Hernández Ortega¹* y Feliberto Fernández Castañeda¹

¹ Departamento de Ingeniería Mecánica. Facultad de Ingeniería Mecánica. Universidad Central "Marta Abreu" de Las Villas. Carretera a Camajuaní Km 5 ½. Santa Clara, Villa Clara, Cuba.

*Autor para la correspondencia: Robert Hernández, Email: [e-mail]

 

 

---

RESUMEN

Los Contornos de Bloqueo son un método gráfico, que muestra al diseñador de engranajes el conjunto de valores de los coeficientes de corrección, que cumple con las limitaciones geométricas de socavado, factor de recubrimiento, interferencia y espesor del diente en el diámetro exterior de las ruedas. En este trabajo se desarrolla un modelo matemático, que permite la construcción no interactiva del Contorno de Bloqueo en transmisiones por engranajes cilíndricos con contacto exterior con dientes asimétricos. Para ello se modifican las ecuaciones que definen las restricciones mencionadas y se establece la secuencia en que deben ser calculadas. De esta manera resulta posible la utilización analítica de los límites del contorno para establecer la dependencia entre los parámetros geométricos de estas transmisiones facilitando así la tarea de síntesis. 

Palabras clave: Contorno de Bloqueo, coeficientes de corrección, engranajes.

 

---

ABSTRACT

Blocking Contours are a graphical method. By means of this technique, the gear designer obtains the values of the correction coefficients, which meets the undercutting geometric constraints, contact ratio, interference and teeth pointing. This paper presents a mathematical model that allows non-interactive construction of blocking contour in the field of cylindrical external gears with asymmetric teeth.For this purpose, the equations defining the mentioned restrictions are modified and it is set the sequence in which they should be calculated. This makes possible the analytical use of the limits of blocking contour for establishing the dependence between the geometric parameters of these transmissions, thereby facilitating synthesis work.

Key words: Blocking Contours, correction coefficients, gear.

 

---

 

 

INTRODUCCIÓN

La utilización de dientes asimétricos es una forma de adecuar una transmisión por engranajes a las características específicas de la máquina, lo que resulta en un diseño más compacto y económico. El diente asimétrico se compone de dos perfiles denominados de ataque y de respaldo, a quienes corresponden respectivamente los ángulos de presión menor y mayor. Ello provoca que la síntesis de la transmisión sea una tarea complicada, particularmente, la selección de los coeficientes de corrección, lo cual fue abordado por (Cárdenas y col., 2011) y (Timofieyev y Samailova, 2012).

Una técnica muy utilizada para la corrección del dentado de las transmisiones por engranajes en general es el método gráfico de los Contornos de Bloqueo planteado por (Bolotovski y col., 1986), que muestra al diseñador de engranajes la zona de existencia de la transmisión, desde el punto de vista de los coeficientes de corrección de las ruedas. Su utilización, en el caso de las transmisiones por engranajes con dientes asimétricos, se reduce a la superposición de los Contornos de Bloqueo, construidos independientemente para cada uno de los ángulos de presión de la herramienta. Como bien reportan (Simeonov y Tsvetanov, 2011), la zona de existencia de la transmisión por engranajes con dientes asimétricos la delimita el área común a ambos perfiles.

El avance acelerado de los medios informáticos ha posibilitado el desarrollo de varias aplicaciones, que permiten la construcción automatizada del Contorno de Bloqueo. De esta manera, es posible la obtención de la zona válida de los coeficientes de corrección, para cualquier combinación de números de dientes y parámetros de la herramienta, de una manera rápida y sencilla. En este sentido se destacan los trabajos de (Mekhalfa et al., 2007), Sholenikov (2008), (Nenov et al., 2011), Němček (2007) y (Goldfarb y Tkachev 2011) en el dominio de las transmisiones por engranajes cilíndricos y de (Kolotov et al., 2013), (Nenov et al., 2013) y (Timofieyev y Samailova, 2012), en la síntesis de engranajes planetarios. Sin embargo, en estas aplicaciones, la obtención del contorno se realiza interactivamente de manera gráfica. Es decir, el diseñador tiene que medir con las herramientas del software la coordenada que desea obtener. El autor desarrolló en su tesis doctoral la automatización no interactiva del método de los Contornos de Bloqueo para engranajes cilíndricos con contacto exterior Hernández-Ortega (2014).

A partir de lo anterior se desarrolló un modelo matemático, que permite la construcción no interactiva del Contorno de Bloqueo en transmisiones por engranajes cilíndricos con contacto exterior con dientes asimétricos, el cual se expone en este trabajo. De esta manera, los valores límites de la zona de existencia de la transmisión pueden ser utilizados de forma analítica para establecer la dependencia entre los parámetros geométricos de las ruedas, lo que facilita la tarea de síntesis.

MATERIALES Y MÉTODOS

2.1. El método de los Contornos de Bloqueo

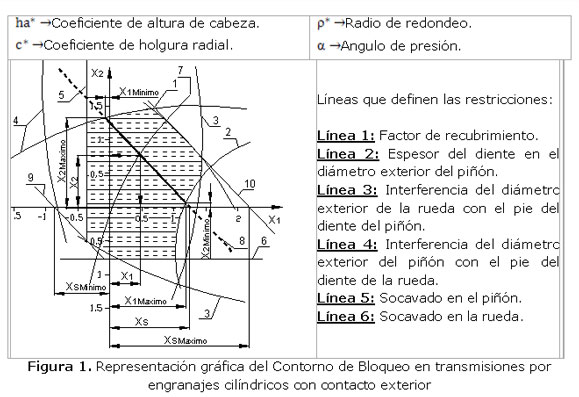
Los Contornos de Bloqueo son un método gráfico, cuyos principios fundamentales para su construcción fueron desarrollados por el ingeniero ruso Israel Bolotovski hace más de 60 años. Esta técnica consiste en la introducción, en un sistema de coordenadas: coeficiente de corrección de la rueda (x₂) versus coeficiente de corrección del piñón (x₁), las curvas que definen las restricciones geométricas de socavado, interferencia, factor de recubrimiento y espesor mínimo del diente en el diámetro exterior de las ruedas (Fig. 1). El conjunto de valores de x₁ y x₂ encerrados por estas curvas delimita la zona de existencia o dominio, de la transmisión definida por los números de dientes del piñón (z₁) y la rueda (z₂), el ángulo de inclinación del diente (β) y los parámetros de la herramienta.

La introducción de las curvas en el área gráfica se realiza a partir de las ecuaciones de cada restricción geométrica expresadas para módulo unitario. La condición de socavado en su forma más general es la siguiente: (Bolotovski y col., 1986):

Ecuación 1

Dónde:

Ángulo de presión de la herramienta en el plano frontal:

Ecuación 2

Ecuación 3

Parámetros de la herramienta:

El factor de recubrimiento se obtiene por la ecuación: (Bolotovski y col., 1986):

Ecuación 4

Dónde:

 Ángulo de presión en el diámetro primitivo medido en el plano frontal.

 Factor de recubrimiento mínimo

 Ángulo de presión en el diámetro exterior medido en el plano frontal, que se obtiene de la ecuación:

Ecuación 5

do_1,2Diámetros de las circunferencias base.

Diámetros exteriores de las ruedas.

El espesor mínimo del diente en el diámetro exterior de las ruedas, medido en el plano normal: (Bolotovski y col., 1986):

Ecuación 6

La condición de no interferencia se expresa por la siguiente inecuación: (Bolotovski y col., 1986):

Ecuación 7

La utilización práctica del Contorno de Bloqueo se sustenta en el hecho de que una transmisión con un valor de corrección sumaria (x_s) dado, se representa en el sistema de coordenadas x₂=f(x₁) como una recta inclinada a 45 grados (ver línea 8 de la figura 1), definida por la ecuación: (Bolotovski y col., 1986):

Ecuación 8

Los puntos limitados por la intersección con los bordes del contorno (x_1Mínimo, x_2Máximo) y (x_1Máximo, x_2Mínimo) definen el intervalo de valores de los coeficientes de corrección que cumplen con todas las limitaciones geométricas. Debido a que el conjunto de combinaciones posibles entre los puntos señalados resulta demasiado amplio, se introducen en el área gráfica curvas que  constituyen indicadores de calidad en el trabajo de las ruedas. Así, por ejemplo, la línea 7 de la figura 1 representa la igualdad del deslizamiento específico entre los dientes.

De igual forma, las líneas 9 y 10 de la figura 1 representan las transmisiones con las distancias entre centros mínima y máxima posibles. Ello implica, que una vez definidos los parámetros geométricos de una transmisión, el Contorno de Bloqueo también está definido y tiene que cumplirse, por tanto, la condición siguiente:

Ecuación 9

 2.2. Contorno de Bloqueo en engranajes con dientes asimétricos

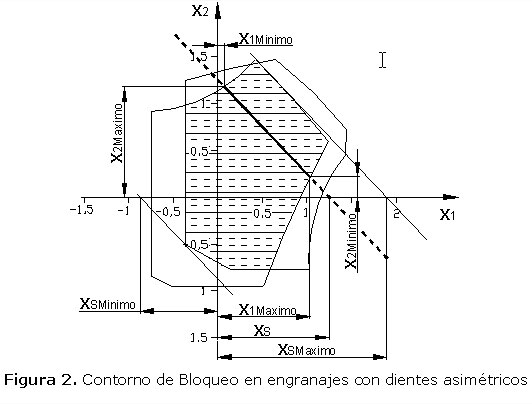
En transmisiones por engranajes con dientes asimétricos la zona de existencia de la transmisión es el área común de los contornos construidos independientemente para cada uno de los perfiles (ver figura 2).

 

Los puntos limitados por la intersección con los bordes del contorno (x_1Mínimo, x_2Máximo) y (x_1Máximo, x_2Mínimo), de la recta que representa las transmisiones con un mismo valor de corrección sumaria x_s, definen el intervalo de valores de los coeficientes de corrección, que cumplen con todas las limitaciones geométricas en ambos perfiles. Se observa, que para la construcción no interactiva del contorno es suficiente obtener el segmento definido por los puntos x_1Mínimo y x_1Máximo para un número suficiente de valores de x_s. Aquí, x_1Mínimo es el mayor valor de los coeficientes de corrección mínimos de cada una de las limitaciones geométricas en ambos perfiles. Asimismo, x_1Máximo es el menor valor de los coeficientes de corrección máximos de cada una de las limitaciones geométricas en ambos perfiles.

Para el cálculo de los valores límites de x₁, para cada una de las limitaciones geométricas en cada uno de los perfiles, se necesita transformar sus respectivas expresiones de manera que sea posible su automatización. En esta investigación se logra transformando las ecuaciones 1, 4, 6 y 7 en función de x₁, mientras que el valor de x₂ se obtiene por la ecuación 8. Así, los valores mínimos  y máximos  del coeficiente de corrección del piñón, que garantizan el factor de recubrimiento mínimo se obtienen por las siguientes ecuaciones:

Ecuación 10

Ecuación 11

Donde:

Ecuación 12

Ecuación 13

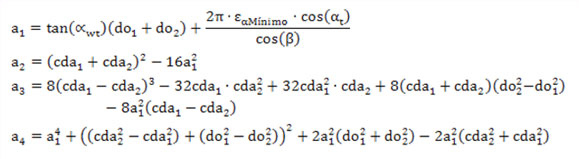
El coeficiente de corrección mínimo, que garantiza la no interferencia entre los perfiles de las ruedas, se determina por la siguiente ecuación:

Ecuación 14

Dónde:

 

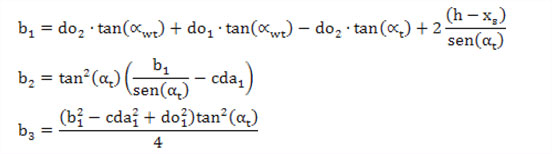
Y el coeficiente de corrección máximo:

Ecuación 15

Dónde:

 

Los coeficientes de corrección mínimo y máximo, que garantizan el espesor mínimo del diente en el diámetro exterior de las ruedas no se pueden obtener por expresiones analíticas, por tanto, es necesario utilizar métodos numéricos. Para ello, la expresión 6 se expresa en función de x₁ por medio de las ecuaciones 5, 8 y 16. De esta manera, se obtienen las expresiones 17 y 18, que representan la variación del espesor del diente en función del coeficiente de corrección del piñón. Se utiliza el método de Newton para calcular x_1máximoS_a1 y x_1mínimoS_a2, mientras que para calcular x_1mínimoS_a1 y x_1máximoS_a2 se aplica  el método de Hamming.

Ecuación 16

Ecuación 17

Ecuación 18

Así, para un valor de corrección sumaria definido, se obtiene el intervalo x_1mínimo…..x_1máximo (ver figura 2), donde la variable x_1mínimo es el mayor de los valores de x₁ calculados por las ecuaciones 1, 10, 14, 17 y 18, para cada uno de los perfiles. Asimismo, el valor de x_1máximo es el menor de los valores máximos de x₁ calculados por las ecuaciones 1, 11, 15, 17 y 18, para cada uno de los perfiles.

El cálculo comienza en el valor máximo de corrección sumaria calculado por la ecuación 19 para cada uno de los perfiles, asignando al ángulo de presión en el plano frontal el valor de tres grados. Asimismo, el cálculo termina en el menor valor de corrección sumaria, calculado para cada uno de los perfiles para un ángulo de presión igual a 45 grados. Ello se debe, a que según (Bolotovski y col., 1986), es improbable la existencia de un Contorno de Bloqueo válido fuera de ese intervalo. Para recorrer todos los valores posibles de corrección sumaria se utiliza un paso de 0,1. Cuando el intervalo x_1mínimo…..x_1máximo aparece por primera vez se utiliza el método de la bisección para obtener x_Smínimo con una precisión de 10 ^-3. De igual manera se calcula x_Smáximo, cuando el intervalo x_1mínimo…..x_1máximo desaparece por primera vez.

Ecuación 19

La metodología expuesta permite establecer la relación geométrica entre las variables que definen una transmisión por engranajes cilíndricos con contacto exterior de dientes asimétricos, mediante la utilización analítica del método de los Contornos de Bloqueo. Así, por las ecuaciones 19 y 20 se obtienen los valores mínimo y máximo de la distancia entre centros para módulo unitario ( utilizando los valores mínimo y máximo de la corrección sumaria. De esta manera, la expresión 9 establece la manera exacta en que se relaciona el módulo y la distancia entre centros para una combinación definida de los parámetros de la herramienta, números de dientes de las ruedas y el ángulo de inclinación del diente.

Ecuación 20

 

2.3. Criterios de calidad en la selección de los coeficientes de corrección

2.3.1. Igualdad del deslizamiento específico

La máxima resistencia al desgaste se obtiene al igualar el deslizamiento específico en cada extremo de la línea práctica de engranaje. Considerando las expresiones 5 y 16, esta condición se expresa matemáticamente, según (Bolotovski y col., 1986), por la ecuación siguiente:

Ecuación 21

Los valores de x₁ que cumplen la condición anterior se obtienen aplicando el método de la bisección en el intervalo x_1mínimo …x_1máximo.

2.3.2. Factor de recubrimiento máximo

El coeficiente de corrección del piñón , donde es máximo el factor de recubrimiento se obtiene de la siguiente manera:

Si  se utiliza la ecuación:

Ecuación 22

Si  se utiliza la ecuación:

Ecuación 23

Las ecuaciones 22 y 23 se obtienen al hallar las raíces de la primera derivada de la ecuación 4 expresada en función de x₁ por medio de las expresiones 5 y 16.

 

2.3.3. Igualdad de resistencia a la flexión

Para obtener la máxima resistencia a la flexión de las ruedas se debe cumplir la condición:

Ecuación 24

 Coeficiente de forma de las ruedas.

 Resistencia permisible a la flexión del material de las ruedas.

Debido a la complejidad matemática para el cálculo del coeficiente de forma que se ofrece en la Norma ISO 6336, el valor de x₁ que cumple la condición anterior se obtiene mediante el método de la bisección aplicado al intervalo x_1mínimo …..x_1máximo.

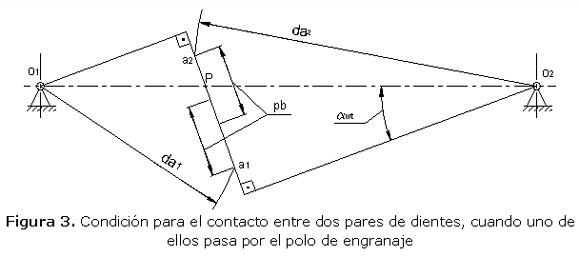
2.3.4. Zonas de dos pares de dientes en contacto, cuando uno de ellos pasa por el polo de engranaje

Algunos autores, entre ellos (Bolotovski y col., 1986) afirman, que la resistencia a la fatiga superficial de las ruedas se puede mejorar si se garantizan dos pares de dientes en contacto, cuando uno de ellos se encuentra en el polo de engranaje. De acuerdo a la figura 3, esto es posible si se cumple una de las siguientes condiciones:

Ecuación 25

Ecuación 26

Dónde: pb→Paso por la circunferencia base.

Al expresar las condiciones 25 y 26 en función de la geometría de las ruedas, y considerando además la ecuación 16, se obtienen las ecuaciones siguientes:

Ecuación 27

Ecuación 28

Ecuación 29

Ecuación 30

De esta manera, se garantizan dos pares de dientes en contacto, cuando uno de ellos se encuentra en el polo de engranaje, si el coeficiente x₁ se encuentra dentro de uno de los intervalos definidos por las ecuaciones 27 y 28 o 29 y 30.

Se debe destacar que en las ecuaciones de la 21 a la 30 se utiliza el ángulo de presión de la herramienta que corresponde al perfil de ataque.

RESULTADOS Y DISCUSIÓN

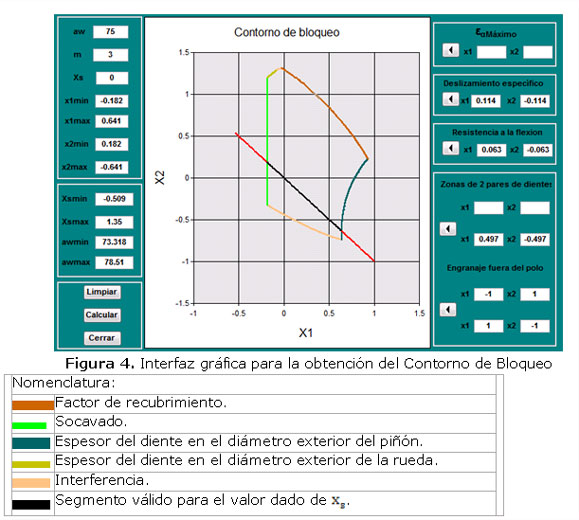
En la Figura 4 se muestra la interfaz gráfica de un software, que utiliza el modelo matemático descrito para la obtención no interactiva del Contorno de Bloqueo en transmisiones por engranajes con dientes asimétricos. Los datos de la transmisión, cuyo contorno se muestra, son los siguientes:

Aquí se destaca, que el gráfico tiene una función solamente ilustrativa, ya que el diseñador no realiza ninguna acción sobre él. Esta es la característica principal de este programa que lo hace diferente a los demás sistemas, que se utilizan para la obtención del Contorno de Bloqueo en engranajes con dientes asimétricos, referenciados en la bibliografía. De esta manera, el método del Contorno de Bloqueo puede ser utilizado por cualquier especialista sin necesidad de tener un conocimiento profundo sobre las particularidades de su construcción.

Asimismo, la obtención no interactiva de los límites del contorno hace posible establecer la dependencia entre los parámetros geométricos de las transmisiones por engranajes con dientes asimétricos de forma analítica, lo que resulta más sencillo en comparación con la forma tradicional. Así, por ejemplo, para los datos mostrados en la figura 4, los límites de existencia de transmisiones, según la condición 9, son los siguientes:

 

Ello implica que al variar un parámetro geométrico, por ejemplo, al asumir un valor de distancia entre centros igual a 80 mm, el módulo tiene que estar en el intervalo:

 

Por lo que se puede afirmar con seguridad absoluta, que para los datos definidos, en el sistema métrico no existe un valor del módulo normalizado que pueda ser utilizado en la síntesis de una transmisión.

De manera análoga sucede en el caso de los límites de los coeficientes de corrección. Así, para la transmisión con , que se muestra en la figura 4, los límites de los coeficientes de corrección son los siguientes:

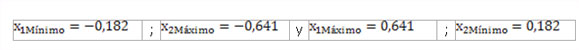
Ello implica, que la selección definitiva de los coeficientes de corrección tiene que estar en el intervalo indicado. Así, por ejemplo, no pueden ser seleccionados los coeficientes de corrección que corresponden a un factor de recubrimiento máximo, como se muestra en la figura 4.

 

CONCLUSIONES

1. En la actualidad el método de los Contornos de Bloqueo se utiliza de manera automatizada en aplicaciones como la síntesis de transmisiones planetarias y     transmisiones por engranajes cilíndricos con contacto exterior e interior. Sin embargo, no se constató en la literatura especializada, la construcción no interactiva     del Contorno de Bloqueo en engranajes cilíndricos con contacto exterior con dientes asimétricos.

2. En engranajes con dientes asimétricos, la construcción no interactiva del Contorno de Bloqueo posibilita la utilización analítica de los límites del contorno para     establecer la dependencia entre los parámetros geométricos de estas transmisiones. Así, a partir de los valores máximos y mínimo de corrección sumaria     (ecuaciones 19 y 20) se obtienen los valores mínimo y máximo de la distancia entre centros para módulo unitario. De esta manera, se establece la condición     matemática (expresión 9) en que se relaciona el módulo y la distancia entre centros para una combinación definida de los parámetros de la herramienta, números de     dientes de las ruedas y el ángulo de inclinación del diente.

3. El modelo matemático desarrollado posibilita la selección definitiva de los coeficientes de corrección de las ruedas a partir de los valores límites obtenidos,     considerando además las condiciones reales de explotación.  De esta manera, se facilita la tarea de síntesis de las transmisiones por engranajes cilíndricos con     contacto exterior con dientes asimétricos.

 

REFERENCIAS

Bolotovski, I.A., Bezrukov, O.F., Vacilieva, B.I., Cálculo Geométrico de Transmisiones de Perfil Evolvente por Engranajes y por Tornillo Sin Fin., Original en Ruso, 2da Edición, Moscú, Construcción de Maquinarias, 1986, pp. 28-138.

Cárdenas, J., Moya, J., Hernández, D., Determinación de los factores geométricos para el cálculo a flexión de los engranajes cilíndricos de dientes rectos asimétricos con perfil de evolvente y trocoide., Revista Ciencia e Ingeniería, Vol. 32, No. 3, 2011, pp. 151-162, [Consultado el 15 de Septiembre del 2015]. Disponible en: http://erevistas. saber.ula.ve/index.php/cienciaeingenieria/article/view/3537

Goldfarb, V. I., Tkachev, A. A., Optimization Approach to Computer-Aided Design of Spur and Helical Gears., Memoirs of 13^th World Congress in Mechanism and Machine Science, Guanajuato, México, 2011, pp. 1-6, [Consultado el 15 de Diciembre 2013], Disponible en: http://somim.org.mx/conference_proceedings/area.html

Hernández-Ortega, R., Construcción analítica del Contorno de Bloqueo aplicada a un Sistema Basado en Casos para el diseño de engranajes cilíndricos con contacto exterior., Tesis e opción al grado Científico de Doctor en Ciencias Técnicas en la Universidad Central Marta Abreu de las Villas, Cuba, 2014.

Kolotov, A.V., Merko, V.A., Mesnyankin, M.V., Resultados de la Solución del Problema de la Determinación de la Zona Común de Selección de los Coeficientes de Desplazamiento de la Transmisión por Engranajes del Tipo 2K-h., (En Ruso). Viestnik de la Universidad Técnica de Tadzhikistan, Vol. 22, No. 2, 2013,  pp. 26-29, [Consultado el 15 de Diciembre 2013], Disponible en: http://www.ttu.tj /userfiles/vestnik/vn22.pdf

Mekhalfa, A., Hadjadj, E., Kallouche, A., Cylindrical Teeth's Gear in Devellopante of Circle., Journal of Engineering and Applied Sciences, Vol. 2, No 1, 2007, pp. 121-124, [Consultado el 15 de Diciembre 2013], Disponible en: http://medwelljournals. com/abstract/?doi=jeasci.2007.121.124

Nenov, P., Ronkova, V., Angelova, E., Almanac of Information Materials, 3d Images, Animations and other Visualizations as an Aid in Studying Machine Elements, Memoirs of 7^th International Conference Research and Development of Mechanical Elements and Systems, Zlatibor, Serbia, 2011, pp.119-126, [Consultado el 15 de Diciembre 2013], Disponible en: http://phdproject.uni-ruse.bg /files/article/paper-IRMES2011-BGRUSE.pdf

Nenov, P., Kaloyanov, B., Angelova, E., Geometrical Blocking Contours as an Instrument for High-Technology Design of Geometry of Involute External and Internal Gear Drives., Mechanisms and Machine Science, Vol. 13, 2013, pp. 379-388, [Consultado el 15 de Diciembre 2013], Disponible en: http://link.springer. com/chapter/10.1007/978-94-007-6558-0_29#page-1

Němček, M., Design of a non Standard Internal Gear Pair.,  Transactions of the VSB-Technical University of Ostrava, Vol LII, No. 1, 2007, pp. 141-145, [Consultado el 15 de Diciembre 2013], Disponible en: http://transactions.fs.vsb.cz/2007-1/1541.pdf

Simeonov, S., Tsvetanov, G., Practical Implementation and Optimization of Evolvent Cylindrical Toothed Gears with Asymmetric Tooth Profile., Machines Technologies Materials, Vol.5, No. 6, 2011, pp. 41-44, [Consultado el 3 de Mayo 2012], Disponible en:http://mech-ing.com/journal/Archive/2011/6/174_Simeonov_Tsvetanov_eng.pdf

Timofieyev, G. A., Samailova, M. V., Zona de existencia de un Mecanismo Planetario de Onda., (En Ruso), Viestnic MGTU Bauman H E Serie: Construcción de Maquinaria, No. 2, 2012, pp. 117-122, [Consultado el 15 de Diciembre 2013], Disponible en: http://vestnikmach.bmstu.ru/articles/98/98.pdf

 

 

Recibido: Octubre 24, 2015;
Revisado: Noviembre 11, 2015;
Aceptado: Noviembre 25, 2015;