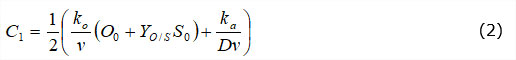ARTICULO

 

Estudio del impacto ambiental del vertimiento de aguas residuales sobre la capacidad de autodepuración del río Portoviejo, Ecuador

 

Study of the environmental impact of wastewater discharges on the self-purification capacity in portoviejo river, ecuador

 

 

Luis Santiago Quiroz Fernández^1*, Elena Izquierdo Kulich² y Carlos Menéndez Gutiérrez³

¹Facultad de Ciencias Matemáticas, Físicas y Químicas. Universidad Técnica de Manabí. Av. Urbina y Che Guevara, Portoviejo, Manabí, Ecuador.
² Facultad de Química. Universidad de La Habana. San Lázaro y L. Vedado. Habana, Cuba.
³ Facultad de Ingeniería Química. Instituto Superior Politécnico José Antonio Echeverría (CUJAE). Av. 114 #11901 e/ Rotonda y Ciclovía, Marianao, Habana, Cuba.

*Autor para la correspondencia: Luis Santiago Quiroz, Email: [e-mail]

 

 

---

RESUMEN

El trabajo propone el estudio del impacto ambiental causado por los vertimientos de aguas residuales en la cuenca del río Portoviejo, mediante la evaluación de su capacidad de autodepuración a través del empleo de un modelo matemático. Se presentan las consideraciones que se deben tomar en cuenta para la aplicación del modelo, la ubicación de los vertimientos y los parámetros del modelo ajustados a partir de los datos experimentales que muestran la variación de la concentración de oxígeno disuelto con respecto a la longitud corregida de la corriente tomando en cuenta la morfología del río. A partir de estos parámetros se calcularon los valores de las constantes de velocidad de reoxigenación y consumo de oxígeno, los cuales se toman como base para la identificación de la sección del río más crítica y de los vertimientos que afectan más significativamente la capacidad de autodepuración.

Palabras clave: contaminación de ríos; impacto ambiental; río Portoviejo; vertimientos; autodepuración.

 

---

ABSTRACT

The paper proposes the study of the environmental impact caused by the wastewater discharges in the Portoviejo River basin, through the evaluation of its self-purification capacity through the use of a mathematical model. It also shows the considerations to be taken into account for the application of the model, the location of the dumps and the model parameters adjusted from the experimental data showing the variation of the dissolved oxygen concentration regarding the corrected length of the stream considering the morphology of the river. From these parameters, the values of the re-oxygenation rate and oxygen consumption constants were calculated, which are used as the basis for the identification of the most critical river section and of the spills that affect the most the self-purification capacity.

Key words: pollution of rivers; environmental impact; Portoviejo River; wastewater discharges; self-purification.

 

---

 

 

INTRODUCCIÓN

Es muy probable que ningún tema haya atraído tanto interés y compromiso mundial como lo ha sido desde hace ya varias décadas, y continúa siendo, el relacionado con la temática del medio ambiente, a partir de la convicción de que el medio ambiente concierne y afecta a todos.

Los ríos históricamente se han considerado como fuente de riqueza, al proporcionar el agua imprescindible para la subsistencia y posterior desarrollo de seres vivos. Propicia la fertilidad de los suelos para la obtención de alimentos, y facilita la comunicación entre los pueblos. Sin embargo, el continuo crecimiento de la población humana y la presencia de modelos de desarrollo no sostenibles, han tenido como consecuencia la contaminación de los ríos y la pérdida de la disponibilidad de estos recursos (Kim y col., 2015), (Singh y col., 2016).

Las soluciones de protección o saneamiento de los ríos dependen, entre otros factores, de la capacidad de autodepuración de un residuo que tenga la corriente superficial (Hernández y Macías, 2003), (Olatunji y Osibanjo, 2013). Para describir esta capacidad, se han desarrollado modelos matemáticos que toman en consideración los principales mecanismos de transporte de contaminantes, la depuración natural a través de la degradación por microorganismos presentes en el río y la reaireación (Streeter y Phelps, 1925), (Wang y col., 2013).

Uno de los elementos que puede incidir en el proceso de autodepuración de los ríos es su longitud. Como es conocido, los ríos presentan una morfología irregular, de tal forma que la longitud total de éste entre dos puntos cualesquiera es en realidad mayor que la longitud de la línea recta que une a ambos puntos. La morfología irregular es demasiado compleja para poder describirse mediante la geometría euclidiana, siendo más apropiado el empleo de la geometría fractal (Mandelbrot, 1982).

El río Portoviejo se encuentra ubicado en la provincia de Manabí, Ecuador, y drena un área de 2108 km², constituyendo la principal fuente de agua para una población aproximada de 700 mil habitantes. La falta de planificación y de orientación del crecimiento urbano en esta región, ha generado que las áreas cercanas al río estén siendo ocupadas por asentamientos humanos sin los adecuados servicios sanitarios básicos. Además, la carencia de un apropiado sistema para el tratamiento de las aguas residuales domésticas y la existencia de conexiones ilícitas en los sistemas de alcantarillados, ha provocado en la actualidad grandes problemas de contaminación (Macías y Díaz, 2010).

El presente estudio tiene como objetivo, cuantificar a través del empleo de un modelo matemático la capacidad de autodepuración del río Portoviejo, tomando como base la variación de la concentración del oxígeno disuelto con respecto a la distancia del punto de vertimiento de cada residual e identificar cuáles de estos vertimientos impacta más significativamente en la calidad del agua.

 

MATERIALES Y MÉTODOS

En un trabajo anterior (Quiroz y col., 2016) se propuso un modelo matemático obtenido a partir de las ecuaciones de transporte de masa, el cual describe la variación de la concentración de oxígeno disuelto en la dirección del recorrido de la corriente superficial. El modelo propuesto está dado por (Ecuación 1):

 

 

En la ecuación (1) los parámetros C₁, C₂ y C₃ se estiman mediante técnicas estadísticas de regresión no lineal a partir de los datos experimentales observados de la concentración de oxígeno disuelto O_z  a la distancia z, la cual toma como valor de referencia (z = 0) el punto de vertimiento de agua residual en el río, donde la concentración de oxigeno es O₀. Estos parámetros se relacionan con las constantes de velocidad asociadas a los procesos de remoción de oxígeno y materia biodegradable de acuerdo con las siguientes expresiones (Ecuación 2, Ecuación 3 y Ecuación 4 ):

 

 

 

Donde:

S₀= Concentración de la demanda bioquímica de oxígeno (DBO) en el punto de vertimiento (kg.m^-3)

O_z= Concentración de oxígeno disuelto (OD) a la distancia z del punto de vertimiento    (kg.m^-3)

O₀= Concentración de oxígeno disuelto en el punto de vertimiento (kg.m^-3)

K₀= Constante de velocidad de consumo de oxígeno (s^-1)

k_a= Coeficiente global de transferencia de masa del oxígeno en la interfase aire-agua (reoxigenación) (m.s^-1)

D= Profundidad promedio del río (m)

v= Velocidad de la corriente (m. s^-1)

Y_0/S= Coeficiente de rendimiento oxígeno/sustrato

 

Nótese que para el cálculo de las constantes de velocidad de reoxigenación (k_a) y consumo de oxígeno (k₀), respectivamente, y del producto (Y_0/SS₀) se requiere conocer la velocidad de la corriente y la profundidad promedio del río, de tal manera que se tenga un sistema no lineal de tres ecuaciones algebraicas y tres incógnitas.

El modelo matemático es aplicado en una longitud aproximada de 12 km en el río Portoviejo. Inicialmente se determinaron los puntos de vertimientos en el área total de estudio, mediante la ubicación de los distintos colectores que descargan aguas residuales utilizando la aplicación del Sistema de Posicionamiento Global (GPS). Una vez identificados estos puntos, se estimó la longitud de la corriente, dividiendo la distancia total en varios tramos, considerando como tramo, el punto de vertimiento de una descarga y un punto anterior del siguiente vertimiento. Para la estimación de la longitud de cada tramo, se emplearon las técnicas basadas en la geometría fractal y el tratamiento de imágenes (Mandelbrot, 1982). En este caso, la dimensión fractal del río se determinó a partir de su morfología en 2D utilizando el método de conteo de cajas y el software ImageJ (Falconer, 2003), para el tratamiento de imágenes.

La toma de datos experimentales se realizó en época de seca, ya que el incremento en el caudal del río en época de lluvia dificulta el registro de estos datos. La estimación del ancho y profundidad promedio de la corriente se obtuvo mediante medición directa en varios puntos del río. Los caudales de vertimiento que se generan en cada colector identificado se estimaron mediante el método volumétrico y el caudal promedio del río mediante el flotador (FAO, 1993).

La concentración de oxígeno disuelto se determinó dentro de cada tramo en que se dividió la corriente, utilizando un medidor Milwaukee MW600 en 10 puntos situados a diferentes distancias entre sí. Estas mediciones fueron realizadas tres veces al día, durante un período de 3 días. La determinación de los parámetros del modelo se realizó a partir del ajuste estadístico de los resultados experimentales obtenidos utilizando el método Marquard de regresión no lineal (STATGRAPHICS Plus 5.1).

 

RESULTADOS Y DISCUSIÓN

3.1. Ubicación de los vertimientos y estimación de la longitud del río

En la longitud del río, objeto de estudio, se identificaron 20 descargas de aguas residuales, las cuales se muestran en la Figura 1. A partir de la imagen obtenida mediante el GPS, se determinó un total de 20 tramos.

 

 

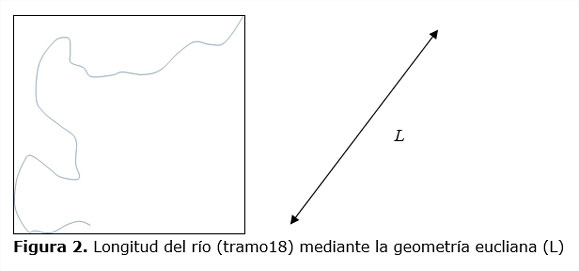
La dimensión fractal calculada se encuentra entre los valores de 1,0182 y 1,2290 para los tramos identificados como 10 y 18, respectivamente. El incremento de la dimensión fractal, corresponde con irregularidades más pronunciadas en la morfología del río, lo que conlleva a un incremento de la longitud real del tramo, en comparación con la que se determina de acuerdo con la línea recta que une el punto inicial y final del tramo considerado, tal como se demuestra en la Figura 2.

 

 

3.2. Concentración de oxígeno disuelto medido a lo largo del río

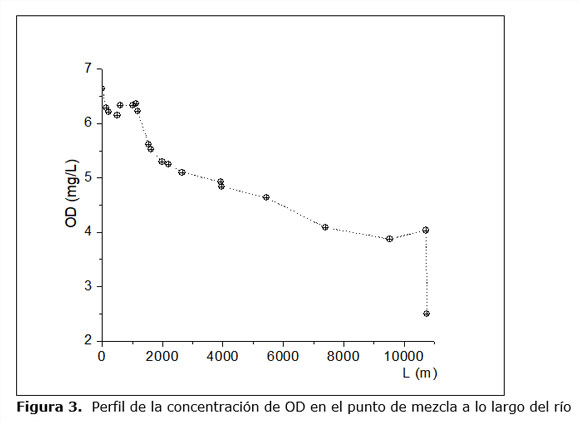
En la Figura 3 se muestra el perfil de los valores de la concentración de oxígeno disuelto a lo largo del río en el punto de mezcla de cada vertimiento. Como se puede apreciar en esta figura los valores correspondientes al oxígeno disuelto desde el vertimiento 1 al 6 se mantienen relativamente constantes, con un valor promedio de 6,30 mg/L (desde el origen hasta 1 125 m), a partir del vertimiento 7 al 12 (desde 1 125 m a 2 649 m)  y del 13 al 20 (desde 2 649 m a 11 600 m), se reducen sus valores significativamente en el orden promedio de 5,30 mg/L y 3,80 mg/L, respectivamente, llegando a un valor extremo al final de la trayectoria igual a 2,50 mg/L.

 

A partir del perfil de los valores de la concentración de oxígeno disuelto, características de cauce y contaminación de cada vertimiento, se decidió dividir la longitud total del cauce del río bajo estudio en tres secciones, donde los criterios tomados en cuenta se muestran en la Tabla 1.

 

 

3.3. Ajuste estadístico del modelo matemático y estimación de parámetros

 

En la Tabla 2 se muestra el modelo ajustado en cada uno de los 20 tramos, los valores de oxígeno disuelto en cada vertimiento (OD_v), el caudal de cada vertimiento (q_v), la longitud estimada para cada tramo (L_TRAMO), así como la posición del punto de vertimiento en el río (L_v) tomando como referencia el punto correspondiente al primer vertimiento o punto cero.

 

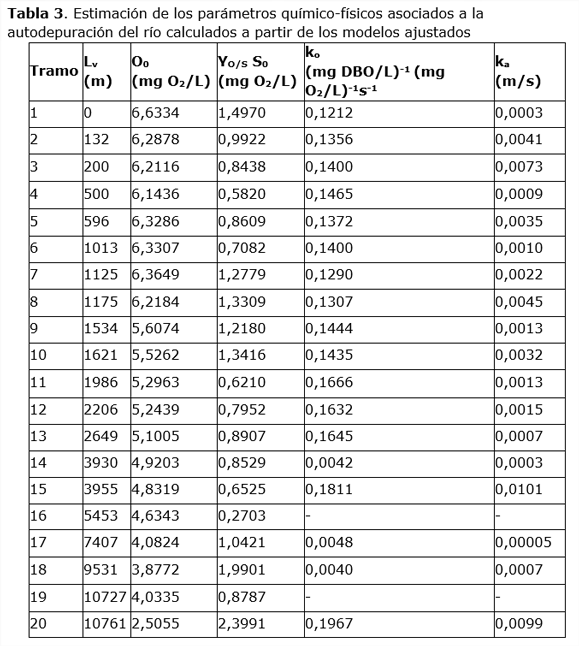
Con los valores C₁, C₂ y C_3, determinados en el ajuste estadístico del modelo en cada uno de los tramos  y a partir de los valores de la velocidad y profundidad promedio de la corriente, el sistema de ecuaciones (2, 3 y 4)  se reduce a un sistema de tres ecuaciones  algebraicas cuya solución permitió la estimación de las constantes de velocidad de consumo de oxígeno ( k₀) y de transferencia de oxígeno a través de la interfase (k_a), así como la resultante del producto del rendimiento oxígeno/sustrato y la concentración de DBO en el punto de mezcla de la corriente del río y el vertimiento (Y_0/SS₀). En la Tabla 3 se muestran los valores estimados de estas constantes para cada uno de los tramos considerados.

 

En la Tabla 3 se muestra que en los tramos 14, 17 y 18 se obtuvieron los valores más bajo de la constante de consumo de oxígeno y de reoxigenación, respectivamente, y que indican los tramos del río en los cuales la capacidad de autodepuración fue menor. En esta Tabla 3 no se reportan valores de k_a y k_a para el caso de los tramos 16 y 19. Esto se debe a que para estos tramos no se detectó un mínimo de concentración de oxígeno disuelto, el cual disminuye con respecto a la distancia a lo largo de toda la longitud del tramo, que implica prácticamente la ausencia de autodepuración. En el ajuste del modelo esto se manifiesta en la estimación de un parámetro de reoxigenación negativo, lo cual carece de sentido físico.

 

3.4. Variaciones de las constantes de velocidad de consumo de oxígeno y de transferencia de oxígeno a través de la interfase

En la Figura 4 se muestra la variación de las constantes de velocidad de consumo de oxígeno (k₀) y de transporte de oxígeno a través de la interfase o reoxigenación (k_a) en cada una de las secciones.

 

Se observa que la constante de reoxigenación no correlaciona con la posición del punto de vertimiento en ninguna de las secciones. En el caso de la sección C se aprecia que en algunos tramos el valor estimado es negativo. Tomando en consideración que estos valores han sido calculados a partir de los parámetros de los modelos ajustados y resultados experimentales observados, no tienen otro significado más allá que el de indicar que en los puntos correspondientes la capacidad de autodepuración del río fue insuficiente para degradar los contaminantes vertidos.

De los análisis realizados se determina que la sección más crítica en la longitud total de estudio es la C (Tabla 1), esto se debe a los valores más bajos de oxígeno disuelto (Figura 3). Tomando en cuenta que los vertimientos de residuales se han hecho sobre una corriente que ya está contaminada debido a los vertimientos previos. En el punto de vertimiento de la ciudadela La Paz, identificado como punto 13, se tiene la menor concentración de oxígeno disuelto, lo que es un indicador de mayor contaminación, y esto se debe a que en esta zona al no existir un sistema de alcantarillado sanitario se producen conexiones ilícitas al sistema pluvial, además, existe un mercado de abastos que, al no contar con un sistema de pretratamiento, las aguas residuales que genera esta actividad (incluyendo limpieza de vísceras) también son descargadas al río. En el sector de la avenida 5 de Junio (punto 16), se constató un vertimiento de aguas residuales producidas por lubricadoras y lavadoras de vehículos, con un contenido significativo de productos químicos que afectan a la población de microorganismos, agravándose el problema porque los hidrocarburos presentes forman una película en la superficie del agua que impide la transferencia de oxígeno y la reoxigenación de la corriente, lo cual causa que la degradación biológica de los contaminantes en esta sección del río sea prácticamente despreciable. El otro punto crítico es el 19, que tiene el mayor caudal de vertimiento, y que corresponde a la salida de la laguna de oxidación donde se tratan las aguas residuales generadas por la mayor parte de la población de la ciudad de Portoviejo, y que presenta una baja eficiencia de operación.

 

CONCLUSIONES

1. La aplicación del modelo matemático propuesto permitió evaluar la capacidad de autodepuración del río Portoviejo a través de la variación de la concentración de oxígeno disuelto con respecto a la distancia del punto de vertimiento, además de identificar cuáles de estos tienen mayor impacto en su contaminación.

2. Se identificó que los vertimientos que afectan en mayor grado la calidad del agua del río Portoviejo son el 13 (Ciudadela La Paz), 16 (Sector avenida 5 de Junio) y 19 (Descarga de la planta de tratamiento de aguas residuales de Portoviejo).

3. Se determinó que la sección más crítica en el área total de estudio es la C (2649m- 11600m), donde los resultados muestran los valores más bajos de la concentración de oxígeno disuelto, debido a que la calidad del agua del río Portoviejo va disminuyendo a medida que avanza su cauce por los vertimientos de aguas residuales que existen a lo largo de su trayectoria. Esto provoca que la corriente vaya reduciendo su capacidad de asimilar la carga contaminante y de restituir su calidad de forma natural.

 

REFERENCIAS

Falconer, K., Fractal Geometry., Mathematical Foundations and Applications, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO198SQ, England, 2003, pp. 1-398.

FAO., Field measurement of soil erosion and runoff., Food and Agriculture Organization of the United Nations (FAO), Bulletin No. 68, 1993, pp. 169-177.

Hernández, A., y Macías, J., Saneamiento ambiental y protección de corrientes., Editorial Félix Varela, La Habana, 2003, pp. 20-65.

Kim, S., Yang, D., y Lim, J., A Study on the Biodegradation of Aquatic Life Using Computational and Physical Simulation., Bulletin of the American Physical Society, Vol. 01, No. 13, 2015, pp. 13-21.

Macías, R., y Díaz, S., Estrategias generales para el control y prevención de la contaminación del agua superficial en la cuenca del río Portoviejo., Ciencias Biológicas, Centro Nacional de Investigaciones Científicas, Vol. 41, 2010, pp.1-7.

Mandelbrot, B., The Fractal Geometry of Nature., Freeman, San Francisco, 1982, pp. 1-460.

Olatunji, O., y Osibanjo, O., Eco-partitioning and indices of heavy metal accumulation in sediment and Tilapia zillii fish in water catchment of River Niger at Ajaokuta, North Central Nigeria., International Journal of Physical Sciences, Vol. 8, No. 20, 2013, pp. 1111-1117.

Quiroz, L., Izquierdo, E., y Menéndez, C., Modelación matemática de la capacidad de autodepuración de corrientes superficiales. Caso de estudio: Río Portoviejo, Ecuador., Revista Cubana de Ingeniería, Vol. 7, No. 2, 2016, pp. 64-70.

Singh, S., Gupta, K., Shukla, N., Chaurasia, G., Singh, S., y Tandon, P., Water purification: A brief review on tools and techniques used in analysis monitoring and assessment of water quality., Green Chemistry & Technology Letters, Vol. 2, No. 2, 2016, pp. 95-102.

Streeter, H., y Phelps, E., A Study of the Pollution and Natural Purification of the Ohio River, United States Public Health Service, U.S. Department  of Health, Education and Welfare, 1925, pp. 889-895.

Wang, Q., Li, S., Jia, P., Qi, C., y Feng, F., A Review of Surface Water Quality Models., The Scientific World Journal, Vol. 2013, 2013, pp. 01-08.

 

 

Recibido: Septiembre 4, 2017
Revisado: Septiembre 27, 2017
Aceptado: Octubre 11, 2017