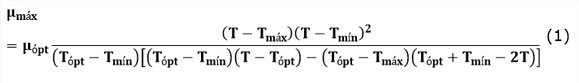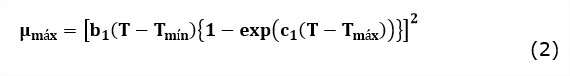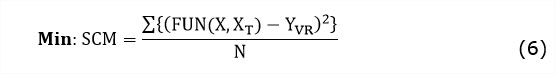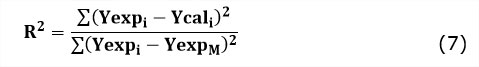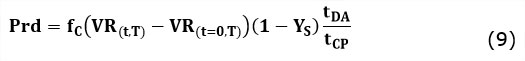ARTICULO

 

Determinación de la temperatura óptima para la producción de celulasas con aspergillus niger en fermentación sólida

 

Determination of the optimum temperature for the cellulase production by aspergillus niger in solid fermentation

 

 

Gualberto Leon-Revelo¹, Mario César Cujilema-Quitio¹, Linnet Baryolo¹, Ernesto Rosero Delgado², Jesús Córdova³ y Luis Beltrán Ramos-Sánchez^1*

¹Departamento de Ingeniería Química, Universidad de Camagüey Ignacio Agramonte Loynaz, Circunvalación Norte km 5 ½, Camagüey, Cuba.
²Universidad Técnica de Manabí. Av. Urbina y Che Guevara, Manabí, Ecuador.
³Departamento de Química. Universidad de Guadalajara. Av. Juárez 976 y América, Guadalajara, México.

*Autor para la correspondencia: Luis B. Ramos, Email: [e-mail]

 

 

---

RESUMEN

En este trabajo se presenta la determinación de la temperatura óptima en la producción de celulasas (PFasa), por una cepa de Aspergillus niger en fermentación sólida, utilizando datos de un modelo cinético propuesto con anterioridad. Fue establecida la dependencia de los 16 parámetros cinéticos en función de la temperatura (en el intervalo de 20 °C a 40 °C). En el caso de los parámetros µ_máx y X_máx, el ajuste se consiguió con calidad con los modelos de Rosso y de Ratkowsky respectivamente. El resto de los parámetros fue necesario ajustarlos con modelos de interpolación cúbica. La dependencia de los parámetros del modelo cinético con la temperatura permitió estimar la temperatura y el tiempo de fermentación óptimo que maximizan la productividad, de la producción de proteína verdadera y de la actividad de las tres enzimas estudiadas, estando la temperatura óptima entre 30°C y 32°C. Para la producción de proteína verdadera y CMCasa, el tiempo de fermentación óptimo se sitúa en 19 horas y 22 horas respectivamente, pero para la producción de PFasa es de 33 horas. La actividad proteasa presenta varios máximos locales en cuanto a temperaturas óptimas que van desde 25 a 40 °C. Aunque los niveles de actividad máximos se sitúan en 64 UI/g_MS que es un valor intermedio según lo reportado en la literatura, el nivel de productividad en actividad PFasa es el mayor encontrado (3,84 veces superior a la actividad promedio), al compararlo con otros 20 reportes consultados desde el año 2004.

Palabras clave: Celulasas, Aspergillus niger, fermentación sólida, cinética, modelación.

 

---

ABSTRACT

Determination of optimum temperature in the (PFasa) cellulase production, by a strain of Aspergillus niger in solid fermentationis presented in this paper, using data from a previously proposed kinetic model. Dependence of the 16 kinetic parameters with temperature (in the range of 20 °C to 40 °C), was established. For µ_max and x_max parameters, the adjustment was achieved using the Rosso and Ratkowsky models respectively. Cubic interpolation models was needed to adjust the rest of kinetic parameters. The dependence of the kinetic model parameters with temperature allowed the estimation of temperature and optimum fermentation time to maximize the productivity in the production of true protein and the activity of the three studied enzymes. As result, the optimum temperature rangeisbetween 30°C and 32°C. For the production of true protein and CMcasa, the optimum fermentation time is located within the19 and 22 hours respectively, but for the production of PFasa, is 33 hours. The protease activity presented several local maxima in terms of optimal temperatures ranging from 25 to 40 °C. Although the maximum activity levels are 64 UI/g_dm, which, according to literature, is an intermediate value, the level of productivity of PFasa is the highest found (3.84 times superior to average activity), when compared with another 20 reports consulted since 2004.

Key words: Cellulase, Aspergillus niger, solid-state fermentation, kinetics, modeling.

 

---

 

 

INTRODUCCIÓN

En la actualidad, uno de los procesos más prometedores para la producción competitiva de celulasas lo constituye la fermentación en estado sólido (FES). Varias son las ventajas tecnológicas que se le atribuyen (Raghuwanshi y col., 2014). Una de estas, es que los hongos filamentosos se expresan en plenitud productiva, quizás debido a que resulta ser un medio semejante al que han tenido en la naturaleza. Dentro de los hongos filamentoso, el género Aspergillus es uno de los más ampliamente utilizados (Ahamed y Vermette, 2008; Santos y col., 2011).

Los modelos cinéticos para la producción de celulasas son escasos en la amplia literatura consultada por los autores, especialmente para procesos de fermentación sólida, en la que sólo se ha hallado un trabajo con estos fines (Piret, 1959) mencionado trabajo presenta un modelo cinético simple para describir la dinámica de la actividad de varias enzimas en un crecimiento modélico del hongo en placas Petri. Como reconocen los autores, en el modelo no se establecen relaciones matemáticas con varias variables del proceso, todo lo cual limita su aplicación. Mientras que el modelo cinético propuesto por los autores de este trabajo está estructurado de forma que se tiene en cuenta la desnaturalización de la enzima por la hidrolisis de las celulasa por las proteasas, y la inhibición de las enzimas debido al máximo crecimiento del microorganismo, esto está dado, porque el microorganismo cuando alcanza su máximo crecimiento ocupa todo su espacio vital y deja de crecer. El modelo cinético ajustado predice a la perfección la producción de las enzimas en el rango de temperatura de 20 a 40 °C.

A todo esto, hay que agregar que en procesos enzimáticos de FES son aún más escasos los estudios dedicados a establecer la dependencia de los parámetros cinéticos con la temperatura. Esta dependencia es imprescindible para resolver los balances de masa y energía que se plantean en el diseño de estos procesos de fermentación, por lo que resulta de gran interés establecer posibles modelos que faciliten esta tarea.

Se conocen varios modelos que describen el efecto de la temperatura sobre los parámetros cinéticos. Resulta difícil establecer a priori qué modelo describirá mejor el comportamiento de los datos experimentales. El análisis de la bibliografía mostró que, dentro de los modelos más usados para procesos de fermentación sólida se encuentran cinco modelos: el modelo de Rosso (Rosso y col., 1995), el modelo Ratkowsky (Ratkowsky y col., 1983), el modelo de Zwietering (Zwietering y col., 1991), el modelo de Esener (Esener y col., 1983) y el modelo de Arrhenius (Levenspiel, 1999).

Partiendo de los resultados previos del ajuste realizado por los autores de un modelo cinético de un proceso de FES celulolítico con una cepa de A. niger, en este trabajo se definió como objetivo identificar la dependencia de los parámetros cinéticos del crecimiento y de la producción enzimática con la temperatura, con vistas a estimar la temperatura y tiempo óptimo para la realización de este proceso productivo.

 

MATERIALES Y MÉTODOS

2.1. Modelo matemático del proceso

2.1.1. Modelo cinético de la actividad del hongo en el medio celulósico

El modelo cinético objeto de análisis fue el propuesto anteriormente (León-Revelo, 2017) para el crecimiento en medio sólido de una cepa de Aspergillus niger. En el trabajo previo fueron determinados, por ajuste no lineal, sus parámetros cinéticos a cinco temperaturas en el rango de 20°C a 40°C, los que se muestran seguidamente:

 

Donde: µ_máx- velocidad específica de crecimiento, (h^-1). Xmáx- concentración máxima del hongo, (g/kg _MS). R²- Coeficiente de correlación del ajuste del modelo

 

Donde: a_PF- Coeficiente de formación de PFasa asociada al crecimiento, (UI g_PV^-1).
a_CMC- Coeficiente de formación de CMCasa asociada al crecimiento,(UI g_PV^-1).
a_Prot- Coeficiente de formación de proteasas asociada al crecimiento (UI g_PV^-1).
b_PF- Coeficientede formación de PFasa no asociada al crecimiento,(UI h^-1 g_PV^-1).
b_CMC- Coeficiente de desactivación de CMCasa no asociada al crecimiento,(UI h^-1 g_PV^-1). b_Prot- Coeficiente de desactivación de proteasas no asociada al crecimiento(UI h^-1 g_PV^-1).

 

Donde: k₁-Velocidad específica de hidrólisis de PFasa por las proteasas,(UI_PF UI_Prot^-1).K₂- Velocidad específica de hidrólisis de CMCasa por las proteasas, (UI_CMC UI_Prot^-1).a_ART-Coeficiente de formación de ART asociada al crecimiento, (g_ART UI^-1).
b_ART - Coeficiente de desactivación de proteasas no asociada al crecimiento,(g_ART g_PV^-1).Y_XS- Rendimiento proteína verdadera/fibra bruta,(g_PV g_FB^-1).Y_P- Rendimiento Proteasa/Fibra bruta,(UI g_FB^-1).Y_PF- Rendimiento PFasa/Fibra bruta,(UI g_FB^-1)

2.2. Modelos para la dependencia de los parámetros cinéticos con la temperatura

Los modelos empleados fueron cinco. Serán escritos en función del parámetro µmáx, pero fueron aplicados a los 16 parámetros identificados, con lo cual la interpretación física de µ_ópt(Parámetro asintótico de los modelos de Rosso y Zwietering), cambia en función del parámetro que sea ajustado respecto a la temperatura:

Modelo cardinal de Rosso (Rosso y col., 1995):

 

Modelo cuadrático expandido de Ratkowsky (Ratkowsky y col., 1983):

 

Modelo de Zwietering (Zwietering y col., 1991):

 

Modelo de Esener (Esener y col., 1983):

 

Ecuación de Arrhenius (Levenspiel, 1999):

Donde: T- Temperatura del medio sólido (^oC). T_máx- Límite de temperatura máxima en los modelos (^oC). T_min- Límite de temperatura mínima en los modelos; 1, 2 y 3 (^oC).
T_ópt- Temperatura óptima (^oC). b₁- Parámetro de la ecuación de Ratkowsky (C^-1 h^-0,5). C₁- Parámetro Ratkowsky (C^-1). C₂- Parámetro Zwietering (C^-1). A- Factor de frecuencia de la activación de la enzima (depende del parámetro). E_A1- Energía de activación (kJ/mol). R- Constante universal de los gases (8,314 kJ mol^-1 K^-1). Be- Factor de frecuencia de la desactivación de la enzima (depende del parámetro). EA₂- Energía de desactivación de la enzima (kJ mol^-1). E_A-Energía de activación (kJ mol^-1)

 

Las unidades de los parámetros de estos modelos se reportan en la literatura referenciada y, sólo la de los modelos mejor ajustados serán reportados en este trabajo. Estos modelos fueron escritos inicialmente para representar la dependencia de la velocidad específica de crecimiento máxima (µ_Máx) con la temperatura. En este trabajo, sin embargo, la existencia de esta relación será extendida a todos los parámetros cinéticos. De esta manera, el parámetro µ_Ópt, de las ecuaciones (1) y (3) se corresponde con el parámetro que se esté analizando, representado en estas ecuaciones por µ_Máx.

Cuando ninguno de estos modelos consiguió un ajuste con la calidad adecuada, la dependencia del parámetro específico se hizo con polinomios cúbicos de interpolación. En este caso, para obtener los coeficientes de este polinomio, se utilizó la función de interpolación de MATLAB: PCHIP (Piecewise Cubic Hermite Interpolating Polynomial) (Fritsch y Carlson, 1980). La interpolación se realiza con la función: PPVAL. Para mayor información consultar las páginas de ayuda del programa MATLAB®, versión: 8.3.0.532 (R2014a)

 

2.3. Identificación de los parámetros cinéticos asociados a la temperatura

Los parámetros empíricos de las ecuaciones (1) a la (4) fueron identificados con los datos estimados antes mostrados en las Tabla 1, tabla 2 y tabla 3, para las cinco temperaturas estudiadas. Con este fin, el programa de ajuste fue elaborado en la plataforma de cálculo MATLAB. Para la identificación de los parámetros cinéticos se hizo uso de una herramienta de ajuste no lineal multifactorial: lsqcurvefit. Esta función usa algoritmos para resolver el problema de optimización en la que se minimiza la suma de cuadrados medios de los residuos dada por:

 

En este caso, en la ecuación (6) el término FUN(X, X_T) representa a un vector que contiene las respuestas calculadas para el vector de la variable independiente (X_T) del modelo dado por las ecuaciones (1) a la (5); para una combinación dada de los parámetros del modelo, representados aquí por el vector (X) y N, el número total de puntos experimentales. El término (Y_VR) representa el vector o matriz que contiene los resultados experimentales de las variables respuestas.

La elección del mejor modelo se hizo con el grado de ajuste a los datos experimentales, medido éste por la menor suma de cuadrados de los residuos, escogido de entre todos los modelos analizados. Adicionalmente, fueron empleados el coeficiente de determinación (R²) y el coeficiente de variación de los residuos (CVR, %) para analizar la calidad del ajuste logrado por el modelo escogido.

 

 

Donde: Yexp_i- son los valores de cada variable respuesta, medidos experimentalmente, Ycal_i, son los valores de cada variable respuesta, estimados por el modelo,  Yexp_M, es la media de los valores experimentales de la variable respuesta dada, SCM es la suma de cuadrados medios asociada a cada variable respuesta.

 

2.4. Estimación de la temperatura y el tiempo óptimos de fermentación

2.4.1. Procedimiento de optimización

La determinación de la temperatura y el tiempo óptimos de fermentación, según el criterio cinético de máxima productividad, se realizó con la herramienta de Matlab para la optimización multifactorial, con restricciones: fmincon. La productividad en términos generales se definió como:

 

Donde: VR_(t,T) y VR_(t=0,T) son las diferentes variables respuestas utilizadas como criterios de productividad en un tiempo dado y para el tiempo cero; t_DA es el tiempo anual disponible para la campaña productiva (h año^-1),t_CP es el tiempo que dura un ciclo productivo (h) y Y_S, es la humedad del sólido (g_Agua g_total^-1).

Se utilizaron cuatro criterios de productividad: se calculó la productividad en base a la biomasa producida (proteína verdadera),en base a la actividad CMCasa, PFasa y proteasa, que son las variables de mayor interés desde el punto de vista cinético para este proceso. La optimización de la actividad proteasa puede mostrar información importante para el diseño del proceso.

En el caso de la productividad de la biomasa el factor de conversión f_C (1x10^-3) se usa para expresar la productividad en unidades de kilogramos de proteína, mientras que en el caso de las actividades enzimáticas (f_C=1x10^-3) es para expresarla en millones de unidades internacionales (MUI). En todos los casos la productividad se expresa por año y por kilogramo de medio total fermentado.

Se tomó como tiempo disponible anual, el equivalente a 11 meses de 30 días de trabajo por año y, como tiempo de un ciclo productivo (t_CP), el correspondiente al tiempo de fermentación más dos horas de tiempo auxiliar para carga, descarga, limpieza y esterilización de biorreactor.

En futuros trabajos, estas variables podrán ser establecidas en función de criterios técnicos y económicos. No obstante, resulta de interés conocer los valores óptimos del tiempo de fermentación y de temperatura para este caso ideal isotérmico, pues servirá de paradigma a alcanzar durante el diseño del proceso. Nótese que la calidad del ajuste de estos dos parámetros queda soportada, no solo por el alto coeficiente de determinación (R²) sino también, por los bajos niveles del coeficiente de variación medio de los residuos.

 

RESULTADOS Y DISCUSIÓN

3.1. Ajuste de los parámetros cinéticos a la temperatura

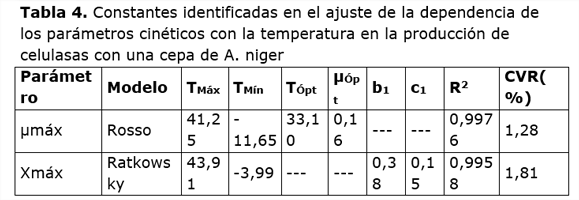
El ajuste de los diferentes parámetros mostró que sólo los parámetros µmáx y Xmáx consiguen un ajuste satisfactorio con los modelos de Rosso y Ratkowsky respectivamente. La tabla 4 muestra los coeficientes identificados para estos dos casos.

 

En la ecuación de Rosso y Ratkowsky los términos T_Máx y T_Mín son las temperaturas (°C) en las cuales el parámetro ajustado se hace cero. En la ecuación de Rosso; T_Ópt representa la temperatura en la cual µ_Máx se hace máxima. Obsérvese que el modelo de Rosso la temperatura óptima de 33,1°C, valor éste que se sitúa entre los reportados anteriormente para el crecimiento de esta cepa. Según este modelo, a la temperatura óptima, la velocidad específica de crecimiento de esta cepa es elevada (µ_Máx=0,16 h^-1), si se compara con las reportadas por (Shahriarinour y col., 2011) cuyos valores oscilan en un rango de: 0,0041 a 0,0071 h^-1, para la producción de celulasas con Aspergillus terreus. Otros autores, (Saithiy col., 2016), reportan una µ_Máx de sólo: 0,081 h^-1 para la producción de biomasa y enzimas con Aspergillus niger en FES.

En el modelo Ratkowsky el parámetro b₁ es el coeficiente de regresión de la raíz cuadrada de la velocidad de crecimiento versus la temperatura por debajo de la temperatura óptima, mientras que c₁ es un parámetro adicional que permite al modelo representar los datos para las temperaturas por encima de la temperatura óptima. Estos parámetros tienen una funcionalidad más matemática que física y su interpretación carece de interés metabólico.

El ajuste del resto de los parámetros cinéticos de la Tabla 2 y de la Tabla 3, no pudo ser alcanzada de forma satisfactoria con los modelos de las ecuaciones (1) a la (5).En estos casos, la relación matemática con la temperatura fue establecida satisfactoriamente usando la función cúbica de interpolación PCHIP de MATLAB. En estas circunstancias, cada parámetro ajustado expresa una matriz de 4x4 de coeficientes, lo cual, es un volumen de información muy elevado para ser incluido en este trabajo. Su reproducción, sin embargo, es muy simple y se puede obtener en MATLAB con la función antes mencionada y los datos de las referidas tablas. Como se observa en esas tablas, estos parámetros muestran una sensibilidad notable con la temperatura y en muchos casos muestran coeficientes de variación (CV) mayores a 20 %.Los parámetros α_cmc, β_cmc, Y_XS, Y_P y Y_PF, muestran un CV más moderado pues se encuentran en un rango de 9 a 20 %. Estos parámetros representan relaciones estequiométricas del modelo metabólico ajustado con anterioridad, tal como se desprende de la formulación realizada. El sistema de reacciones metabólicas es relativamente más estable en un medio dado y su modificación sólo ocurrirá para valores extremos de las condiciones nutricionales y ambientales del cultivo.

 

3.2. Validación del modelo con parámetros dependientes de la temperatura

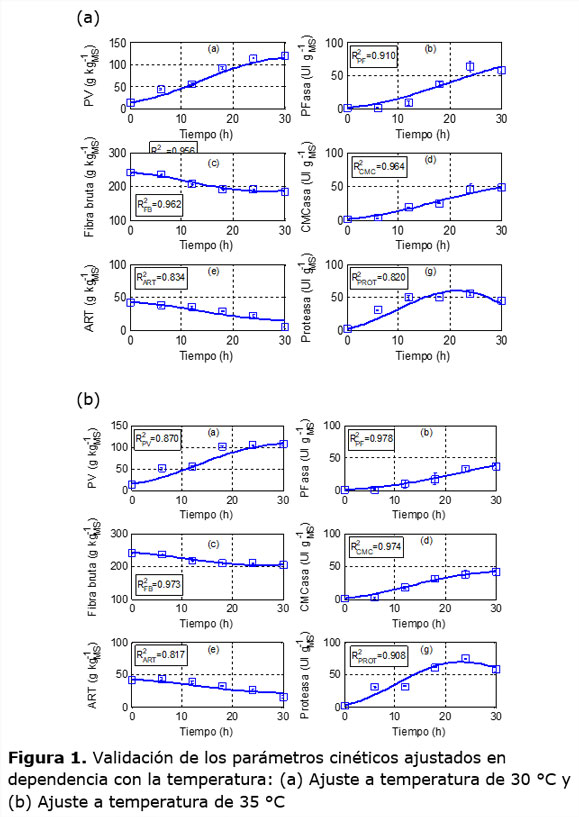
Una vez obtenidos los coeficientes para cada uno de los parámetros, se simuló el comportamiento de la fermentación a las diferentes temperaturas que fueron usadas en el experimento cinético. Los valores predichos con el modelo de parámetros dependientes de la temperatura fueron representados en la figura 1 junto con los valores experimentales. Los valores del coeficiente de determinación calculados para estos pares de datos revelan la buena correspondencia entre éstos.

 

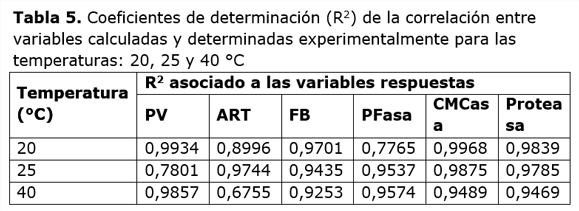
También se obtuvieron buenos ajustes a las temperaturas de 20, 25 y 40 °C como muestra la Tabla 5.La buena correlación del modelo con los datos mostrados indica la posibilidad de su uso para simular el comportamiento del proceso en el rango de 20°C a 40°C.

 

Donde: PV- Proteína verdadera. ART- Azúcares Reductores Totales. FB- Fibra Bruta. PFasa- Actividad en papel de filtro. CMCasa- Actividad a carboximetil celulosa. Proteasas- Actividad proteasa.

3.3. Estimación de la temperatura y tiempo óptimo de fermentación

Los resultados del cálculo del tiempo y la temperatura óptima de fermentación se muestran en la Tabla 6 para las tres productividades antes relacionadas.

 

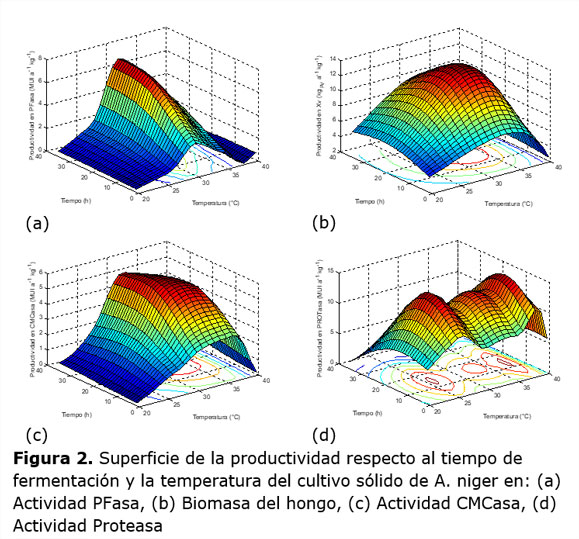
Si se comparan los resultados para el tiempo y la temperatura para los tres primeros criterios de optimización, se notará que en el caso de la PFasa el tiempo de fermentación se aleja bastante de los correspondientes a la proteína verdadera y la actividad CMCasa. Este comportamiento se explica por la forma de la superficie de la productividad para esta actividad mostrada en la Figura 2, dependiente del modelo cinético para esta enzima. En este caso se observa un crecimiento casi monótono de la productividad con el tiempo, por lo que se considera que el tiempo óptimo estimado es correspondiente a un máximo local. Esto no sucede así para la productividad en la proteína verdadera, Figura 2(b), y en CMCasa, Figura 2 (c), las que presentan un claro punto máximo en el entorno mostrado de sus superficies. Si la función objetivo fuera costo unitario de la enzima el escenario sería diferente pues con el tiempo los costos totales se acumulan de forma que debe haber un cambio mucho más claro en el signo de la pendiente.

En estos tres casos las temperaturas muestran una evidente inflexión en la productividad en niveles que van aproximadamente de 30 °C a 32°C para los tres criterios de efectividad analizados. La temperatura es un factor muy influyente y selectivo en la actividad de un microorganismo debido a su naturaleza catalítica. En este caso las tres variables medidas están asociadas al metabolismo primario de la célula, por lo que no es de extrañar que tengan temperaturas óptimas semejantes, en el rango óptimo reportado para esta especie de hongo filamentoso.

La superficie de la actividad proteasa presenta un comportamiento totalmente diferente, con tres zonas de máxima productividad (Figura 2d): una a 25,9°C, otra en 33,4°C y, la más elevada a 37,8°C. Este comportamiento indica la existencia de tres tipos de proteasas. En este trabajo, sin embargo, no se hizo una caracterización molecular de las enzimas, por lo que no se pudo comprobar esta hipótesis.

En los tres casos antes mencionados, el tiempo en el que se alcanza la máxima productividad proteasa está entre 14 y 15 horas, un corto lapsus. La rápida acumulación de estas enzimas obedece a la necesidad de aprovechar las fuentes de nitrógeno proteico que posee el medio de cultivo utilizado, que contiene extracto de levadura y el afrecho cervecero, ricos en material proteico que son claves para el mejor desempeño de la célula en su actividad vital.

 

El comportamiento del sistema de enzimas celulasas puede funcionar bien si se controla de forma adecuada la temperatura del proceso en el intervalo de 30°C a 32°C donde no sólo el crecimiento celular y la actividad celulasa se hacen máximos, (ver Figura 2 a, b y c) sino que, además, la actividad proteasa tiene un extremo local mínimo (Figura 2d).

 

3.4. Comparación de los resultados en actividad PFasa con otros reportes en la literatura

A partir de los datos proporcionados por Hansen (Hansen y col., 2015) que realiza una revisión bibliografía sobre la producción de celulasas, se observa que el nivel óptimo de PFasa establecido en este trabajo, supera a 11 datos reportados por ese autor. Esos datos se obtuvieron utilizando fermentación sólida, con varias especies y géneros de hongos filamentosos.

La productividad de PFasa resulta superior 3,84 veces respecto al promedio de productividad de los trabajos consultados (Hansen y col., 2015). Lo que destaca en este trabajo, no es tanto el nivel de actividad PFasa, que se sitúa en un nivel medio, sino el breve tiempo en que se alcanza. Esto  demuestra una ventaja competitiva para este cultivo pues, en casi 50 trabajos que se reseñan (Hansen y col., 2015), el tiempo promedio de fermentación es de 6,2 días y el valor que más se repite (moda) es de 4 días. Como el tiempo del ciclo productivo es directamente proporcional al tiempo de fermentación, entonces, el proceso productivo de este trabajo produciría 7,44 veces más enzimas que el promedio de los procesos reportados en FES.

Esto equivaldría a tener una actividad de 476,90 UI gMS^-1, si su tiempo de fermentación fuera igual al promedio, y de 307,68 UI gMS^-1, si su tiempo de fermentación fuera igual a la moda. Esta última actividad PFasa es 1,26 veces superior a la más alta encontrada en la literatura, según la reseña que se realizó hasta el año 2015 (Hansen y col., 2015).

 

CONCLUSIONES

1. Los parámetros µ_máx y X_máx se ajustaron su dependencia con la temperatura con los modelos de Rosso y Ratkowsky y el resto de parámetros se ajustó con modelos polinómicos empíricos.
2. La dependencia de los parámetros del modelo cinético con la temperatura permitió estimar la temperatura y el tiempo óptimo de fermentación, que maximizan la productividad de la producción de proteína verdadera y la actividad de la enzima celulasas (PFasa y CMCasa), la temperatura óptima está entre 30°C y 32°C., mientras que el tiempo de fermentación óptimo se sitúa en 19 horas para proteína verdadera y 22 para la CMCasa, pero para la producción de PFasa es de 33 horas.
3. La actividad proteasa presenta varios máximos en cuanto a temperaturas óptimas, el rango va desde 25 a 40 °C. Resulta interesante estudiar la actividad proteasa con más detalles en el futuro.
4. Aunque los niveles de actividad máximos se sitúan en 64 UI/gMS que le corresponde un valor intermedio según lo reportado en la literatura, el nivel de productividad en actividad PFasa es el mayor encontrado al compararlo con otros 20 reportes consultados desde el año 2004 (3,84 veces superior a la media).

 

AGRADECIMIENTOS

La realización del trabajo de investigación que ha servido de base para esta publicación ha contado con el apoyo de la Secretaría Nacional de Educación Superior, Ciencia Tecnología del Ecuador (SENESCYT) y de la Universidad de Camagüey Ignacio Agramonte Loynaz de Cuba.

 

REFERENCIAS

Ahamed, A. y Vermette, P., Enhanced enzyme production from mixed cultures of Trichoderma reesei RUT-C30 and Aspergillus niger LMA grown as fed batch in a stirred tank bioreactor., Biochemical Engineering Journal, Vol. 42, 2008,pp. 41–46.

Esener, A., Roels, J. y Kossen, W., Theory and application of unstructured growth models kinetic and energetic aspects., Biotechnology and Bioengineering,Vol. 25, 1983, 2803-2841.

Fritsch, F. N. y Carlson, R.E., Monotone Piecewise Cubic Interpolation,. SIAM J. Numer. Anal., Vol 17, No. 2, April, 1980, pp. 238-246.

Hansen, G., Mette, L., Jens, F., Peter, L. y Birgitte, A., Production of cellulolytic enzymes from ascomycetes: Comparison of solid state and submerged fermentation., Process Biochem., Vol. 50, No. 9, 2015, pp. 1327-1341.

León-Revelo, G., Diseño de un proceso a escala piloto para la producción de celulasas por  fermentación sólida con residuos agroindustriales.,Tesis presentada en opción al Grado Cientíco de Doctor en Ciencias., Departamento de Ingeniería Química., Universidad de Camagüey, 2017.

Levenspiel, O., Chemical Reaction Engineering., John Wiley & Sons, New York, 1999, pp. 27-29.

Piret, L.R., A Kinetic study of the lactic acid fermentation: batch process at controlled Ph., J Biochem Microbiol Technol Eng,Vol. 1, 1959, pp. 393-412.

Raghuwanshi, S., Deswal, D., Karp, M. y Kuhad, R. C., Bioprocessing of enhanced cellulase production from a mutant of Trichoderma asperellum RCK2011 and its application in hydrolysis of cellulose., Fuel, Vol. 124, 2014, pp. 183-189.

Ratkowsky, D., Lowry, R., McMeekin, T., Stokes, A. y Chandler, R., Model for Bacterial Culture Growth Rate Throughout the Entire Biokinetic Temperature Range., Journal of Bacteriology, Vol. 154, No. 3, 1983, pp. 1222-1226.

Rosso, L., Lobry, J., Bajard, S. y Flandrois, J., Convenient Model To Describe the Combined Effects of Temperature and pH on Microbial Growth., Applied And Environmental Microbiology, Vol. 61, No. 2, 1995, pp. 610-616.

Saithi, S., Borg, J., Nopharatana, M. y Tongta, A., Mathematical Modeling of Biomass and Enzyme Production Kinetics by Aspergillus niger in Solid-State Fermentation at Various Temperatures and Moisture Contents., Journal of Microbial & Biochemical Technology, Vol. 8, 2016, pp. 123-130.

Santos,T.C.d., Cavalcanti, I.S., Bonomo, R.C.F., Santana, N.B. y Franco, M., Optimization of productions of cellulolytic enzymes by Aspergillus niger using residue of mango a substrate., Ciência Rural, Vol.41, 2011, pp. 2210-2216.

Shahriarinour, M., AbdulWahab, M.N., Ariff, A.B., Mustafa, S. y Mohamad, R., Kinetics of cellulase production by Aspergillus terreus at various levels of dissolved oxygen tension in a stirred tank bioreactor., BioResources, Vol. 6, 2011, pp. 4909-4921.

Zwietering, M., Koos, J., Hasenack, B., Wit, J. y Riet, K.V.T., Modeling of Bacterial Growth as a Function of Temperature., Applied And Environmental Microbiology, Vol. 57, No. 4, 1991, pp. 1094-1101. 

 

 

Recibido: Enero 24, 2017
Revisado: Mayo 12, 2017
Aceptado: Enero 5, 2018