INTRODUCCIÓN
Un parámetro importante a tener en cuenta en la producción de quesos es el rendimiento, el cual se ve afectado fundamentalmente por la composición de la leche; en particular el contenido de caseína y materia grasa y por las operaciones empleadas en el proceso tecnológico, entre ellas: la formación, el corte y la elaboración de la cuajada (Martínez y González, 2014), Costa (2015). Después que se determina la composición de la leche, es importante el control en estas etapas para minimizar las pérdidas de componentes de la leche en el suero y obtener una cuajada de cuerpo, textura, acidez y humedad deseados.
Durante los últimos años en la industria alimentaria se ha extendido de manera considerable el uso de sistemas dirigidos al mejoramiento de los rendimientos productivos, los cuales no solo tienen como objetivo aplicar herramientas de mejora continua, sino crear y hacer más eficaz el funcionamiento de la industria (Hernández y García, 2012). Estas herramientas se basan en el análisis de un sistema, proceso o parte de éste, mediante el empleo de la modelación matemática en conjunto con la simulación de procesos como medio de aplicación y validación de los modelos matemáticos (González y col., 2006), (García y col., 2015), (Sariego y col., 2017).
La utilización de modelos multivariados que relacionen los parámetros de operación fundamentales de la producción de quesos, específicamente en la etapa de obtención de la cuajada con el rendimiento resulta de gran importancia para la industria quesera. La aplicación de modelos estadísticos en dicha etapa permitirá establecer, cuáles de las variables del proceso inciden más en los resultados de la misma y además, contar con un modelo matemático para simular y evaluar las condiciones de operación que permitan lograr mayores rendimientos en el proceso de producción, minimizando las pérdidas de materias primas y el consumo energético Aliaskina (2015), (Balzarini y col., 2015).
El queso Gratina producido es una fuente de ganancias significativas para la fábrica en estudio, debido a la escala de producción el mismo. Sin embargo, su rendimiento en los últimos años ha sido alrededor de 8,2% Aliaskina (2015), siendo un valor bajo, lo que trae consigo una menor cantidad de quesos producidos y menos ingresos. Con vistas a mejorar el rendimiento se hace necesario realizar un análisis de las condiciones de operación en la cuba quesera, dado que es una de las etapas más críticas del proceso.
De acuerdo con la problemática planteada se propusieron como objetivo principal establecer la relación funcional entre el rendimiento en la cuba quesera y los parámetros de operación mediante el método de los Mínimos Cuadrados.
MATERIALES Y MÉTODOS
El análisis de la obtención de la cuajada en la producción de queso Gratina se desarrolló con una selección de 16 variables, cuyos valores se recopilaron en seis producciones. Las variables medidas fueron: el volumen de leche que se procesa en la cuba quesera (V), la temperatura inicial (Tle) y final de la leche que llega a la cuba (Tlf), la temperatura ambiente (Ta), la temperatura de adición del cultivo (Tcul) y del cuajo (Tcua), el tiempo de agitación intermedio entre la adición del cultivo y del cuajo (tai), tiempo de agitación final después de añadido el cuajo (taf), tiempo de coagulación (tcoag), tiempo de agitación para el corte de la cuajada (tac), tiempo de reposo antes del desuere (tr), temperatura de cocción (Tc), tiempo de cocción (tc), volumen de agua adicionada (Vag), temperatura del agua adicionada (Tag) y tiempo de prensado (tp).
Para la tabulación y organización de estos datos se utilizó el programa Microsoft Excel y para su posterior procesamiento se empleó el programa Statgraphics Centurion XV.
El análisis multivariado se realizó mediante las etapas siguientes:
Análisis de los datos: Se describió el comportamiento de las variables, calculando para cada una de ellas: el promedio, los valores máximos y mínimos y el coeficiente de variación.
Obtención de Conglomerados: Se utilizó el método del Vecino Más Cercano y la métrica de distancia Euclideana Cuadrada teniendo en cuenta experiencias anteriores en producciones lácteas obtenidas por Mora (2013), (Sariego y col., 2014) y Aliaskina (2015) y se definió la formación de dos conglomerados. Se estandarizó para que todas las variables estuviesen dentro de un mismo intervalo de valores. El análisis se realizó para las observaciones (producciones) buscando diferencias entre ellas.
Cálculo de los Componentes Principales: El procedimiento de Componentes Principales está diseñado para extraer k componentes principales de un conjunto de p variables cuantitativas x (García y col., 2015). Se consideró un porcentaje superior a 85% de la variable explicada en la selección del mínimo de componentes.
Procedimiento para el análisis por Mínimos Cuadrados Parciales (MCP): Se diseñó el procedimiento de MCP para construir un modelo estadístico que relaciona múltiples variables independientes x con múltiples variables dependientes y (Sariego y García, 2013). En el análisis por MCP se tuvieron en cuenta tres componentes principales y 16 variables independientes para obtener los modelos de rendimiento con respecto a la leche. Se obtuvieron los modelos, estandarizando los valores experimentales centrados por la media y sin estandarizar las variables, para poderlos utilizar en la simulación con las unidades de medidas originales de cada variable independiente. La significación de los modelos se comprobó para un 95% de confiabilidad a través del valor-p. La calidad de predicción se analizó a través del valor PRESS (Sumatoria Cuadrada del Error de Predicción).
Los modelos se validaron por el método “sacar uno a la vez” mediante el programa Statgraphics Centurion XV, el cual ajusta el modelo, dejando una producción sin incluir que después se utiliza para calcular el error de predicción. Este procedimiento se repite tantas veces como cantidad de producciones se hayan analizado y finalmente, reporta el promedio de los valores obtenidos en dichos cálculos.
El modelo obtenido por el método de MCP con las variables no estandarizadas se empleó para evaluar alternativas de mejora en las condiciones de operación, buscando que se incremente el rendimiento en la etapa y teniendo en cuenta que los valores de las variables de operación que más favorezcan este propósito estén dentro de los valores alcanzados en las producciones estudiadas. Para ello se tomó en cuenta el signo de los coeficientes de las variables y los valores experimentales. Los coeficientes con signo positivo indicaron los mayores valores de las variables y los de signos negativos representaron los menores valores de la sustitución de las variables estudiadas a simular para obtener el mejor rendimiento.
Para estimar el efecto económico de trabajar bajo las condiciones recomendadas, se calculó el beneficio económico teniendo en cuenta el mayor y el menor rendimiento y el precio de venta establecido para el producto.
RESULTADOS Y DISCUSIÓN
En la tabla 1 y 2 se muestran los estadígrafos que describen el comportamiento de cada variable en la etapa de obtención de la cuajada, antes y después de la coagulación de la leche respectivamente.
Tabla 1 Resumen estadístico de las variables antes de la coagulación de la leche
| Promedio | 5175,0 | 26,1 | 34,7 | 27,8 |
| Coeficiente de variación (%) | 7,8 | 4,8 | 3,9 | 5,6 |
| Mínimo | 4500,0 | 24,0 | 32,6 | 25,2 |
| Máximo | 5500,0 | 27,2 | 36,2 | 30,0 |
| Promedio | 29,7 | 33,8 | 11,5 | 5,2 |
| Coeficiente de variación (%) | 9,8 | 2,5 | 56,8 | 28,5 |
| Mínimo | 26,7 | 32,8 | 4,0 | 4,0 |
| Máximo | 34,0 | 35,0 | 21,0 | 8,0 |
En los resultados de la tabla 1 se puede apreciar que la variabilidad de las temperaturas es pequeña, lo cual conviene, pues la temperatura es un factor de elevada influencia en los procesos bioquímicos de esta etapa, mientras que los tiempos en las producciones tuvieron una elevada variabilidad, lo cual indica que no hay un buen control de estas variables en las operaciones del proceso, pudiendo influir en los rendimientos.
Tabla 2 Resumen estadístico de las variables después de la coagulación de la leche
| Promedio | 29,5 | 5,7 | 2,8 | 38,1 |
| Coeficiente de variación (%) | 48,9 | 34,7 | 26,6 | 5,9 |
| Mínimo | 13,0 | 3,0 | 2,0 | 34,2 |
| Máximo | 45,0 | 8,0 | 4,0 | 40,2 |
| Promedio | 12,2 | 812,9 | 35,1 | 28,0 |
| Coeficiente de variación (%) | 28,6 | 48,6 | 30,8 | 33,3 |
| Mínimo | 10,0 | 504,0 | 22,0 | 20,0 |
| Máximo | 18,0 | 1428,0 | 50,4 | 45,0 |
En los resultados de la tabla 2 se observa que excepto Tc que tiene poca dispersión en las seis producciones, el resto de los parámetros medidos difieren bastante entre una producción y otra. Este es un resultado esperado ya que estos son parámetros que tradicionalmente decide el maestro quesero.
Se puede decir que el tiempo de coagulación (tcoag) determina las características de la cuajada, el que se garantiza mediante el ajuste de la cantidad de cuajo, la temperatura del proceso y la acidez, que son variables controladas y verificadas por el maestro quesero. El lavado de la cuajada, se realiza con el fin de extraer la lactosa, impidiendo un aumento de la acidez. Este proceso lo lleva a cabo también el maestro quesero quien controla el volumen de agua adicionada, así como la temperatura de la misma.
Las correlaciones significativas de las variables estudiadas con una probabilidad de más de un 95% de confianza se presentan en la tabla 3.
Tabla 3 Parámetros de operación correlacionados
| Ta - tc | 0,0041 | 0,9474 |
| Ta - V | 0,0389 | -0,8344 |
| tac - tcoag | 0,0162 | 0,8941 |
| tac - Tcua | 0,0125 | -0,9074 |
| Tc - Vag | 0,0440 | 0,8234 |
| tcoag - Tcua | 0,0484 | -0,8145 |
| Tcul - V | 0,0485 | -0,8143 |
| Tle - tr | 0,0304 | 0,8540 |
| Tlf - tp | 0,0129 | 0,9058 |
En esta tabla se observa que todas las correlaciones son altas, es decir, se manifiesta un vínculo estrecho entre los valores de las mismas, pues todos los coeficientes son superiores a 0,8000. Algunas de estas correlaciones son directas (signo positivo) y otras son inversas (signo negativo).
En la (Fig. 1) se presenta el dendograma obtenido al procesar los datos por el método de conglomerados.
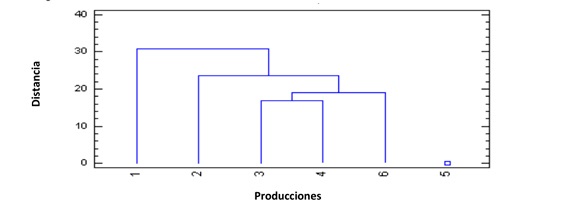
Fig. 1 Dendograma de las observaciones. Método del Vecino Más Cercano con métrica de distancia Euclideana Cuadrada
En esta figura se observa que las producciones que más se parecen fueron la tres y la cuatro, es decir, fueron las que más semejanzas tuvieron entre los parámetros de operación medidos. La producción seis fue la que más se asemejó a las dos anteriores, pues fue con la que se formó el grupo siguiente y la distancia resultó ser inferior a 20. La producción cinco fue la menos parecida al resto, lo cual se debió a que a diferencia de las otras, no hubo cocción ni lavado del grano y esto repercutió en las características de la cuajada obtenida al ser la misma menos compacta. No obstante a este resultado, no se excluyó de la base de datos a procesar para obtener resultados con un mayor espectro de validez al considerar una producción no tan homogénea como el resto y además, su rendimiento fue semejante al de las otras producciones.
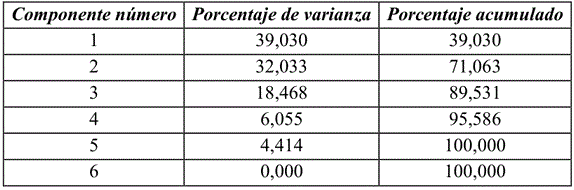
En la tabla 4 se presentan los resultados del Análisis de Compontes Principales obtenidos con el programa Statgraphics Centurion XV.
En la tabla se aprecia que con tres componentes se explica el 89,5% de la varianza total de los puntos experimentales y con cuatro componentes se explica el 95% de la varianza total. Ambos valores son aceptables, considerando que se trata de producciones industriales. Por otra parte, un quinto componente incrementaría muy poco (en solo un 6%) el acumulado de la varianza explicada, por lo que se justifica el uso de tres o cuatro componentes en el ajuste por Mínimos Cuadrados Parciales. Con vistas a obtener un modelo matemático que establezca la relación funcional entre las variables del proceso y los rendimientos en la cuba quesera se aplicó el método de MCP.
Las tablas 5 y 6 presentan el análisis de varianza y de calidad de ajuste de los modelos. En dichas tablas se observa que el modelo de rendimiento con respecto a la leche presentó buena calidad de ajuste para un 95% de confiabilidad, pues el valor-p del análisis de varianza igual a 0,0057 fue inferior a 0,05 que es el límite superior para esta prueba. Además, el PRESS fue un valor del orden de 5,00x10-4 para tres componentes y presentó un coeficiente de determinación (R2) de 99,61%, valor que manifiesta muy buena calidad en la predicción. Si se considera que el mejor modelo siempre es el más sencillo y que posea un buen ajuste, se aplicó este modelo para tres componentes.
Tabla 5 Resultados del ajuste de Mínimos Cuadrados Parciales para el rendimiento con respecto a la leche. Análisis de varianza
| Modelo | 0,000342046 | 3 | 1,14015 x10-4 | 173,554 | 0,0057 |
| Residuo | 0,000001313 | 2 | 6,56944 x10-7 | - | - |
| Total (corr.) | 0,000343360 | 5 | - | - | - |
Tabla 6 Calidad de predicción para el rendimiento con respecto a la leche
|
|
|
|
|
|
|---|---|---|---|---|
| 1 | 80,3844 | 80,3844 | 0,000924129 | 0,0 |
| 2 | 11,7131 | 92,0975 | 0,000538421 | 0,0 |
| 3 | 7,5198 | 99,6173 | 0,000500775 | 0,0 |
En la tabla 7 se muestran los coeficientes con las variables estandarizadas y sin estandarizar para los modelos de rendimiento con respecto a la masa de leche inicial.
Tabla 7 Coeficientes con las variables estandarizadas y no estandarizadas del modelo de rendimiento con respecto a la leche
| B0 | 0,00 | 1,73 x10-01 |
| Ta | 1,27x10-01 | 6,72 x10-04 |
| Tac | -3,74 x10-02 | -1,58 x10-04 |
| Taf | 5,36 x10-02 | 3,02 x10-04 |
| Tag | 1,33 x10-01 | 1,02 x10-04 |
| Tai | -1,26 x10-02 | -1,60 x10-05 |
| Tc | -7,01 x10-02 | -9,89 x10-05 |
| Tc | -2,56 x10-01 | -9,36 x10-04 |
| Tcoag | 8,70 x10-02 | 4,99 x10-05 |
| Tcua | 4,82 x10-02 | 4,81 x10-04 |
| Tcul | 9,54 x10-02 | 2,71 x10-04 |
| Tle | 6,26 x10-03 | 4,15 x10-05 |
| Tlf | -1,75 x10-01 | -1,07 x10-03 |
| Tp | 6,42 x10-02 | 5,71 x10-05 |
| Tr | -7,06 x10-02 | -7,77x10-04 |
| V | -3,80 x10-01 | -7,79 x10-06 |
| Vag | -4,85 x10-01 | -8,30 x10-06 |
B0: Término independiente del modelo
Como resultado de evaluar las variables del proceso sobre el rendimiento con el modelo obtenido por MCP teniendo en cuenta las condiciones más favorables según los signos de los coeficientes y los valores experimentales de las variables se obtuvo que se podía alcanzar un rendimiento de 12,02%. Para estimar el efecto económico de trabajar bajo estas condiciones propuestas, se consideró una producción de 5300 L de leche con una densidad de 1,0256 kg/L. Si el rendimiento es de 12,02% se obtendrían 54,06 kg de cuajada por encima de lo que se obtuvo en la producción de mayor rendimiento (11%), por lo que si se considera que en las etapas posteriores a la formación de la cuajada las pérdidas no son muy grandes y que el precio de venta es de 30,09 $/kg, esto implicaría un ingreso adicional de 1 600,00 CUP (24 CUP es el equivalente a 1 USD). Estos resultados demuestran la posibilidad de evaluar condiciones de operación a través de la simulación con modelos multivariados.
CONCLUSIONES
El modelo de regresión por Mínimos Cuadrados Parciales que establece la relación funcional entre el rendimiento en la cuba quesera y las 16 variables de operación posee un Error Cuadrático de Predicción igual a 5,00x10-4, lo que indica la posibilidad de su empleo para simular esta etapa.
Bajo las condiciones de operación más favorables en la etapa de obtención de la cuajada se pueden obtener rendimientos respecto a la masa de leche inicial de hasta un 12,02%, lo que mejora el resultado en esta etapa. Al trabajar bajo estas condiciones puede lograr un efecto económico de 1600,00 CUP adicionales, que equivale a 54,06 kg de cuajada por encima.