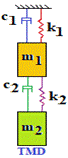INTRODUCCIÓN
La verificación analítica y experimental de la transferencia de energía de un sistema principal excitado externamente a otro sistema secundario no excitado, acoplado al primero, dio origen a los amortiguadores de masa sintonizados, en lo adelante TMD (del inglés: Tuned Mass Damper). El amortiguador de masa sintonizado es una herramienta ingenieril clásica consistente en una masa, un resorte y un amortiguador viscoso colocados en el sistema vibrante principal para atenuar la vibración no deseada a una frecuencia determinada. La frecuencia natural del amortiguador se sintoniza con la frecuencia natural del sistema principal provocando que el amortiguador vibre en resonancia, disipando la energía absorbida a través de los mecanismos de amortiguamiento del TMD (Falconí, 2012). Después de su invención por Frahm en 1909 (Frahm, 1911) el concepto de amortiguadores de masa sintonizados ha atraído la atención de investigadores de diferentes campos para controlar vibraciones causadas por diferentes tipos de fuerzas.
Den Hartog demostró que, para sistemas de un grado de libertad no amortiguado, la amplitud de vibración del sistema excitado es nula cuando la frecuencia de excitación es igual a la frecuencia del TMD, indicando que toda la energía del sistema fue transferida al TMD (Den, 1956). Jones presentó un análisis aproximado de la respuesta debida al modo fundamental de una viga simple de una única luz equipada con amortiguadores sintonizados (Jones, 1967). En particular para cargas en puentes, se estudió el efecto de un TMD en el control de vibraciones en puentes bajo la acción de cargas que se mueven a lo largo de la estructura. Sintonizaron el TMD en el modo vertical dominante y lo instalaron en el medio de los puentes. Además, agregaron masas al modelo con el objetivo de simular las masas de los vehículos para así determinar la respuesta dinámica de los puentes. El autor muestra la eficiencia de los TMD en el caso de un puente con tres luces. Los desplazamientos verticales en el medio del puente fueron comparados antes y después de la instalación de los TMD (Li y Cao, 2019).
Se evaluaron vigas de Timoshenko equipadas con TMD bajo la acción de excitaciones armónicas (Chen y Huang, 2004). Los autores estudiaron la respuesta dinámica de las vigas para un determinado intervalo de frecuencias. Propusieron un modelo simplificado de dos grados de libertad y emplearon el método propuesto por Den Hartog para estudiar las características dinámicas de los TMD presentando algunas tablas de diseño para aplicaciones prácticas. Se realizó un estudio comparativo entre vigas simplemente apoyadas sin dispositivos de control, vigas con un TMD y vigas con múltiples TMD demostrando la eficiencia de los dispositivos de control (Mazzon y col., 2023).
Existe gran variedad de amortiguadores de masa sintonizados que responden a distintas solicitudes como: tipo de estructura y su geometría, cargas y modos de oscilación predominantes, materiales, etc. Los más empleados en edificios para reducir los desplazamientos producidos por el viento son los amortiguadores de masa traslacionales y los amortiguadores de masa pendulares, estos últimos empleados en edificios altos (Padrón, 2021), (Bian y col., 2022). Para el caso de los puentes, se han desarrollado amortiguadores horizontales y verticales. Estos últimos son los de mayor importancia para este trabajo (Martínez-Martínez y col., 2022), (Roozbahan y Turan, 2023), (Chagoyen y col., 2021).
En los puentes el TMD se coloca en la zona con la mayor amplitud de vibración de la frecuencia natural vertical. La fijación del dispositivo a la estructura se realiza mediante tornillos o placas de fijación (Hajji, 2016), (Junfeng y col., 2022).
En este trabajo se determina la influencia de la masa, la rigidez y el amortiguamiento en la amplificación dinámica de la estructura. Se simula el problema real, donde se tiene una estructura y un amortiguador de masa sintonizado para disminuir las vibraciones, en un modelo de uno y dos grados de libertad, y mediante el software de Ingeniería Matlab, se obtiene resultados como desplazamientos y amplitud de las oscilaciones del sistema analizado.
MATERIALES Y MÉTODOS
2.1 Estudio dinámico del sistema formado por la estructura y el TMD
Se realiza un estudio dinámico a partir de los modelos de uno y dos grados de libertad (gdl) para analizar la influencia de la masa, la rigidez y el amortiguamiento en el comportamiento estructural del puente (gdl 1) y el TMD (gdl 2). De estos modelos se obtienen, además, varias gráficas que muestran el desplazamiento de cada grado de libertad y la amplitud de las oscilaciones de la estructura, del TMD y del sistema completo (estructura + TMD).
Sistema con un grado de libertad: Puente sin TMD
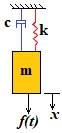
Para simplificar el problema real es necesario realizar un modelo de un solo grado de libertad. El esquema básico tiene la forma que se puede apreciar en la figura 1. La ecuación general que gobierna el problema descrito es la (1):
𝑚𝑥̈+𝑐𝑥̇+𝑘𝑥=𝐴𝑠𝑒𝑛 𝜔𝑓𝑡 (1)
siendo: m la masa (t); c la amortiguación (kN-s/m); k la rigidez (kN/m); A la amplitud (m) y wf la frecuencia asociada a la fuerza (Hz).
El término derecho de la ecuación indica que el sistema está sometido a oscilaciones forzadas, si estuviera sujeto a oscilaciones libres entonces dicho término sería cero.
Otro aspecto a tener en cuenta es la solicitud de las vibraciones en la estructura. En este caso las oscilaciones que se estudian son en la dirección vertical. Es importante aclarar que la gravedad influye en la ecuación de movimiento del sistema: debido al peso propio de los cuerpos existe un pequeño desplazamiento inicial, en este trabajo no se tiene en cuenta la fuerza de gravedad ya que estas condiciones son prácticamente insignificantes, por eso todo el estudio dinámico se realiza después que el sistema se encuentra en equilibrio (Bian y col., 2022).
Para la resolución de la ecuación diferencial que describe el comportamiento de la estructura se emplea el software Matlab. Para una mejor interpretación del cálculo es conveniente transformar la ecuación diferencial de segundo orden en un sistema de dos ecuaciones diferenciales de primer orden. Se introduce para ello la variable y, que representa la velocidad:
Es habitual en estructuras hacer los siguientes cambios de variable:
El sistema de ecuaciones queda, por tanto:
Para desarrollar el código se necesita además del sistema de ecuaciones descrito, un vector que contenga el intervalo de tiempo de integración y otro vector con las condiciones iniciales. El vector de tiempo contiene los valores inicial y final del intervalo, y el vector de condiciones iniciales contiene la posición y velocidad iniciales.
Con el fin de minimizar el error numérico, el intervalo de integración será entre 0 y T, siendo T el periodo asociado a la fuerza que actúa sobre el sistema.
A partir de lo anterior se obtienen resultados importantes para la comprensión del comportamiento del puente sin TMD y su interpretación en relación con el problema real. Con esta metodología se pueden obtener gráficas como las de respuesta en frecuencia variando parámetros como la masa, la rigidez y el amortiguamiento (Hajji, 2016).
La variable que se usa como dato es 𝜉 (relación de amortiguación), pero para la resolución numérica se utiliza el valor de c (amortiguación), que se obtiene despejando de la definición antes realizada.
2.1.2. Sistema de dos grados de libertad: Puente con TMD
Se desarrolla el modelo matemático de dos grados de libertad el cual se acerca aún más al sistema real, donde se tiene la estructura con sus características dinámicas y el amortiguador de masa sintonizado que se le incorporará para reducir la amplitud de sus oscilaciones. El tratamiento de este problema es similar al de un grado de libertad como se puede observar en la figura 2, pero con ciertas consideraciones. En las ecuaciones que gobiernan este problema, existe cierto acoplamiento entre los términos de masa, amortiguamiento y rigidez.
Escrito en forma matricial queda:
donde 𝑀, 𝐶 y 𝐾 son las matrices de masa, amortiguamiento y rigidez, respectivamente. Y 𝑓𝑖(𝑡) el vector de fuerzas. Este vector, dado que este trabajo tiene como fin el estudio del TMD, se puede simplificar teniendo en cuenta que no actúa ninguna fuerza directamente sobre el segundo grado de libertad (f2(t)=0).
En este caso se pasa del sistema de dos ecuaciones de segundo orden a un sistema de cuatro ecuaciones de primer orden, despejando las variables correspondientes de la siguiente manera:
2.2. Caso de Estudio
El caso de estudio consiste en un puente ferroviario ubicado en el km 560 del Ferrocarril Central de Cuba. El mismo presenta cuatro luces de 20 m cada una (figura 3). Una de estas luces tiene una masa m=95 t y una rigidez k=50´000 kN/m. El coeficiente de amortiguamiento que se utilizó en este trabajo fue de ξ=0,025, por ser el valor más utilizado en la literatura (Duménigo, 2018). La excitación del puente se consiguió al hacer pasar una locomotora por encima de este en ambas direcciones a velocidades variables. Como unidad de la masa se empleará la tonelada métrica (t) que es aceptada para su uso con unidades del Sistema Internacional y que habitualmente se emplea en esta propiedad de los puentes.
RESULTADOS Y DISCUSIÓN
3.1 Sistema de un grado de libertad
3.1.1. Influencia de la masa
Si se ejecuta el código para distintos valores de la masa se puede apreciar la influencia de la misma. La masa será la única variable, manteniendo constante todos los demás parámetros del problema, resumidos en la tabla 1.
Tabla 1 Parámetros para el análisis de la influencia de la masa
| ξ | k (kN/m) | A (kN) | wf (Hz) |
|---|---|---|---|
| 0,025 | 50´000 | 20 | 20 |
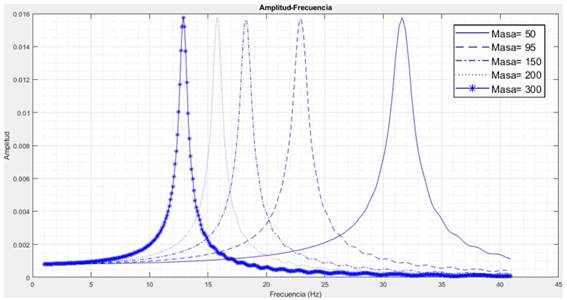
La función de respuesta en frecuencia para distintos valores de la masa aparece en la figura 4. Mientras que en la tabla 2, se recogen los resultados de la gráfica anterior donde se puede visualizar para qué frecuencias se alcanzan los máximos de amplitud para las distintas masas.
Tabla 2 Amplitudes máximas y frecuencias correspondientes para las distintas masas
| Masa (t) | Amplitud Máx.(m) | Frecuencia (Hz) |
|---|---|---|
| 50 | 0,01575 | 31,6 |
| 95 | 0,01571 | 22,9 |
| 150 | 0,01561 | 18,3 |
| 200 | 0,01575 | 15,8 |
| 300 | 0,01576 | 12,9 |
Se puede afirmar que no existe influencia de la masa en la amplitud de la respuesta, pero sí tiene influencia en la frecuencia natural. Cuanto mayor sea la masa, menor es la frecuencia, es decir, para que un sistema con una masa elevada entre en resonancia, la solicitación debe tener un periodo elevado, y viceversa.
3.1.2. Influencia del amortiguamiento
Siguiendo el mismo procedimiento, se mantienen constantes todos los parámetros a excepción del amortiguamiento (𝜉). Los parámetros usados se resumen en la tabla 3.
Tabla 3 Parámetros para el análisis de la influencia del amortiguamiento
| m (t) | k (kN/m) | A (kN) | wf (Hz) |
|---|---|---|---|
| 95 | 50´000 | 20 | 20 |
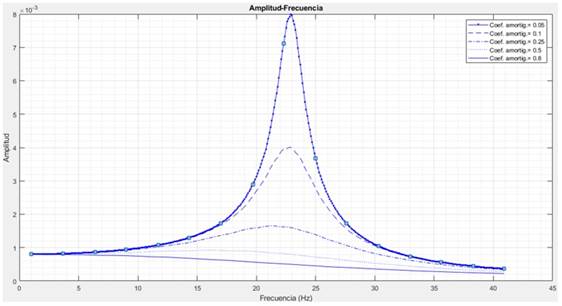
Ejecutando el código se obtiene la función de respuesta en frecuencia para los distintos valores de 𝜉 (figura 5). En la tabla 4 se muestran, para cada coeficiente de amortiguamiento, la mayor amplitud obtenida y su frecuencia correspondiente.
Tabla 4 Amplitudes máximas y frecuencias correspondientes para los valores de ξ
| ξ | Amplitud máx. (m) | Frecuencia (Hz) |
|---|---|---|
| 0,05 | 0,007999 | 22,9 |
| 0,1 | 0,003970 | 22,6 |
| 0,25 | 0,001651 | 21,2 |
| 0,5 | 0,0009236 | 16,1 |
| 0,8 | 0,0007594 | 9,0 |
Las curvas son cualitativamente distintas si se varía el valor del amortiguamiento que, a diferencia de lo que ocurría con la masa, influye tanto en la amplitud como en la frecuencia natural. Cuanto menor sea 𝜉 mayores serán la amplificación dinámica y la frecuencia, el sistema será cada vez menos amortiguado. Si, por el contrario, 𝜉 toma valores cercanos a la unidad, el sistema tiene cada vez menor amplitud y frecuencia natural.
3.1.3. Influencia de la rigidez
De forma similar, al variar la rigidez manteniendo constantes los restantes parámetros, como se muestra en la tabla 5.
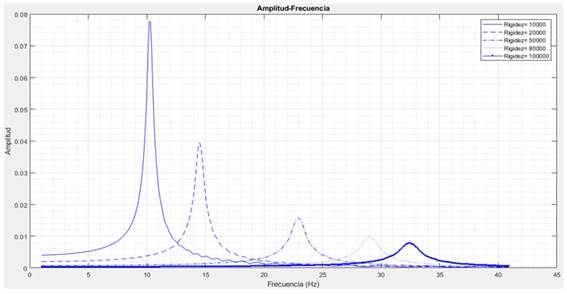
Si se visualiza la función de respuesta en frecuencia para los distintos valores de rigidez, se obtienen las curvas que se muestra en la figura 6. En la tabla 6 se expone la mayor amplitud obtenida y su frecuencia correspondiente para cada valor de rigidez.
Tabla 6 Amplitudes máximas y frecuencias correspondientes para los valores de rigidez
| Rigidez (kN/m) | Amplitud máx. (m) | Frecuencia (Hz) |
|---|---|---|
| 10´000 | 0,07774 | 10,2 |
| 20´000 | 0,03946 | 14,5 |
| 50´000 | 0,01571 | 22,9 |
| 80´000 | 0,009844 | 29,0 |
| 100´000 | 0,007865 | 32,4 |
Para la rigidez la relación es clara, cuando se aumenta la rigidez disminuye la amplitud de la vibración en régimen permanente, a la vez que aumenta la frecuencia natural.
3.2 Sistema de dos grados de libertad
3.2.1. Gráficas de posición-tiempo
Se estudia las gráficas posición-tiempo para los dos grados de libertad, pero antes se debe tener en cuenta que, en el caso de dos grados de libertad, se tienen dos amortiguamientos relativos:
En este caso se considerarán siempre constantes los valores asociados al primer grado de libertad ya que son los parámetros de una estructura que es invariable. Es por ello que para analizar cómo varían los resultados en función del amortiguamiento, sólo se tomará como variable el asociado al segundo grado de libertad, es decir, 𝜉2. A continuación, se obtendrán las curvas posición-tiempo para ambos grados de libertad, dando al amortiguamiento tres valores distintos (𝜉2(%)=7,5; 20; 80). Se tomará el valor del amortiguamiento habitual en estructuras que es de 𝜉1=0,025. El resto de los parámetros utilizados se muestran en la tabla 7.
Tabla 7 Parámetros para el análisis de gráficas posición-tiempo en función de 𝜉2
| 𝒎𝟏 (t) | 𝒎𝟐 (t) | 𝒌𝟏 (kN/m) | 𝒌𝟐 (kN/m) | 𝝃𝟏 | A (kN) | wf (Hz) |
|---|---|---|---|---|---|---|
| 95 | 9,5 | 50´000 | 4´400 | 0,025 | 20 | 20 |
La masa del TMD (m2) se estima según los criterios de (Den, 1956) y (Chen y Huang, 2004) que plantean que existe una relación de masa entre la estructura y el sistema amortiguador sintonizado. Para que los TMD tengan aplicabilidad y funcionalidad, el valor de μ debe estar en un intervalo de valores entre 0,01 y 0,15, o sea, la relación debe estar en el orden del 1 al 15 %. La razón de masa adoptada en este trabajo fue del 10 %, que se encuentra en el rango recomendado por estos autores:
siendo: m - masa del sistema amortiguador (t) y M - masa de la estructura (t).
La rigidez del TMD (k2) se estima asumiendo que su frecuencia natural sea aproximadamente igual que la del sistema principal (22 Hz).
siendo:
Comprobación:
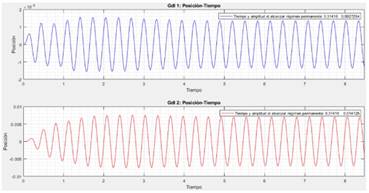
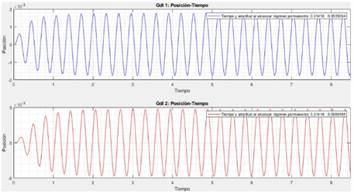
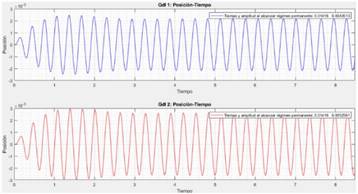
Las curvas de posición-tiempo resultantes para cada gdl aparecen en las figuras 7, 8 y 9.
3.2.2. Función de Respuesta en Frecuencia (FRF)
Desarrollando el mismo código, se pueden obtener las gráficas de amplitud-frecuencia. En este caso, cada grado de libertad tiene asociada una frecuencia de resonancia, por lo que, al combinarlos, se obtiene gráficas con dos picos. El gráfico para el problema se obtiene con las variables que aparecen en la tabla 8.
Tabla 8 Parámetros para análisis de la función de respuesta en frecuencia
| 𝒎𝟏 (t) | 𝒎𝟐 (t) | 𝒌𝟏 (kN/m) | 𝒌𝟐 (kN/m) | 𝝃𝟏 | 𝝃𝟐 | A (kN) | 𝝎𝒇 (Hz) |
|---|---|---|---|---|---|---|---|
| 95 | 9,5 | 50´000 | 4´400 | 0,025 | 0,075 | 20 | 20 |
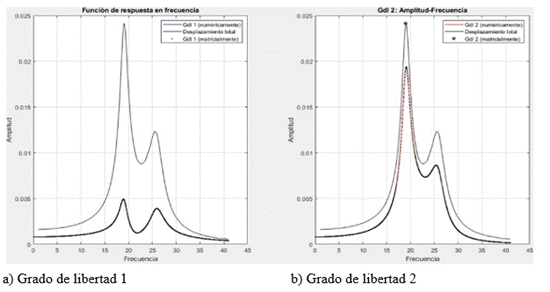
Las funciones de respuesta en frecuencia para cada gdl aparecen en la figura 10.
Aunque usualmente la curva que interesa es la definida como sistema completo, se ha representado por duplicado para que sea visible el aporte de cada grado de libertad al sistema. Como se había anticipado, se trata de una curva con dos máximos claros. Esto es debido a que cada grado de libertad, si se considera por separado, tiene una frecuencia de resonancia asociada que, en este caso, al tener unos valores de amortiguamiento muy bajos, prácticamente coincide con la frecuencia natural. Al unir los dos grados, la gráfica del conjunto que se obtiene es una mezcla de la de cada grado. En el ejemplo analizado se puede hacer un cálculo sencillo para verificar la hipótesis explicada, partiendo de las definiciones de frecuencia natural (ecuación (11)):
En el sistema de dos grados de libertad, la tabla 9 resume los valores obtenidos respecto al tiempo que demora en alcanzar el régimen permanente y la amplitud en el mismo.
Tabla 9 Comparación de los resultados para tres valores de 𝜉2
| ξ2=7,5 % | ξ2=20% | ξ2=80 % | |||||
|---|---|---|---|---|---|---|---|
| gdl 1 | gdl 2 | gdl 1 | gdl 2 | gdl 1 | gdl 2 | ||
| Tiempo | 0,31416 | 0,31416 | 0,31416 | 0,31416 | 0,31416 | 0,31416 | |
| Amplitud | 0,0027254 | 0,014125 | 0,0035054 | 0,0095165 | 0,0043513 | 0,0052561 | |
A partir de las gráficas 7, 8 y 9, se puede describir lo que ocurre al aumentar el valor de 𝜉2:
Para ambos grados de libertad, con estos valores de masa, rigidez, amortiguamiento y amplitud de la fuerza de excitación, el sistema alcanza el régimen permanente rápidamente y cada grado de libertad lo hace prácticamente al mismo tiempo.
La amplitud en el segundo grado de libertad tiende a disminuir, mientras que la del primer grado de libertad aumenta. Esto es debido a que, para bajos amortiguamientos, el grado de libertad dos vibra ampliamente absorbiendo parte de la energía que llega al gdl 1. Si el amortiguamiento es alto, ese gdl 2 no está disipando la energía mediante vibraciones, lo que se traduce en mayores amplitudes en el primer grado de libertad.
En las gráficas de FRF (figura 10) se aprecia que la máxima amplitud de cada grado de libertad aparece aproximadamente para la frecuencia natural correspondiente. No es exactamente igual porque hay un cierto grado de amortiguamiento y los elementos que componen la estructura no son independientes, existe cierto acoplamiento entre ellos.
CONCLUSIONES
1. Se desarrolla un modelo numérico donde se obtiene la influencia de la masa, la rigidez y el amortiguamiento en la respuesta dinámica del sistema, de este estudio se observan los siguientes resultados:
La masa no influye en la amplitud de la respuesta dinámica del sistema. Cuanto menor sea el coeficiente de amortiguamiento de una estructura mayor será la amplitud de sus oscilaciones. La influencia de la rigidez es clara, mientras menor sea la rigidez de un sistema mayor será la amplitud de sus oscilaciones.
Para valores elevados de masa y amortiguamiento de una estructura, menor frecuencia natural tiene; entonces para que un sistema con estos parámetros elevados entre en resonancia, la fuerza de excitación debe tener un período alto.
2. Al resolver el modelo de dos grados de libertad, variando solamente el coeficiente de amortiguamiento del TMD (𝜉2) y obteniendo las gráficas de posición-tiempo, se puede arribar a las siguientes conclusiones:
Para cualquier valor de 𝜉2 se comprueba que el segundo grado de libertad (TMD) vibra ampliamente absorbiendo parte de la energía que llega a la estructura.
Para cualquiera de los grados de libertad (puente o TMD), con estos valores de masa, rigidez, amortiguamiento y amplitud de la fuerza de excitación, el sistema alcanza el régimen permanente rápidamente y cada grado de libertad lo hace prácticamente al mismo tiempo.
3. En las funciones de respuesta en frecuencia, se comprueba que el sistema alcanza su mayor amplificación dinámica cuando la frecuencia de la vibración producida por una carga externa coincide con la frecuencia natural de la estructura.