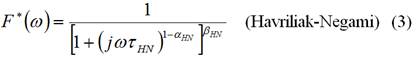Introduction
Lanthanum-modified Lead Zirconate Titanate (PLZT) is a transparent ceramic with a Perovskite structure of the ABO3 type, which is obtained by doping with La3+ ions in the A sites of the starting ceramic, PZT.1 This system, with diffuse ferroelectric phase transition and a marked relaxation character, is useful in biomedical and electro-optical applications such as protectors of intense radiation, in optical memories and displays, as well as in non-volatile memories and pyroelectric detectors.1-9
The ratios of Pb/La at the A sites of the structure, and of Zr/Ti, at the B sites, determine its crystal phase, microstructure, morphology, electrical properties and even its relaxing behavior.1
Thus, with the entry of doping elements in the A and B sites of the crystal structure of this material, its physical properties can be modified and adjusted depending on its applications. There have been several reports related to the effects on the most notable physical properties of PLZT for different compositions, which cause acceptor doping elements in this system, such as Cu, Mn, Fe, Co, etc.1,3,4,10-13
In order to maintain the neutrality of the charge and conservation of mass, the inclusion of these impurities brings about the generation of punctual defects in the structure (vacancies and interstices) that affect the microstructure and the physical properties of the material.1,14-16
Ajeet Kumar et al. reported that PLZT (7/82/18) doped with manganese at 0,0; 0,1; 0,2 and 0,5 % experienced a decrease in losses and in the dielectric constant as manganese concentration 2 increased.
Some reports 4,17 have referred to a dispersion of permittivity with frequency for temperatures greater than τ_m, generating a relaxing behavior at high temperatures, which suggests the presence of a conductive process that can influence the functionality of the material.17
For the study of relaxation in conductive processes, one of the most appropriate formalisms is the electrical module formalism. This complex quantity M* (ω) is calculated as the inverse of the permittivity ε* (ω).18
Conductivity mechanisms can be studied using relaxation processes. The analysis of these processes is commonly carried out in the frequency domain through empirical expressions, starting from the Debye expression, for the adjustment of the experimental dielectric spectra. Among the most accepted expressions are Cole-Cole (C-C, 1941), Davidson-Cole (D-C, 1951) and Havriliak-Negami (H-N, 1966) /18/, which are given by:
Where and HN) are the relaxation times of each of the relaxation distribution functions and the frequency. In these equations, the values of α and β are adjustment parameters, which range between 0 and 1.
Md. Ahamad Mohiddon et al. found that manganese-doped PLZT (8/65/35) showed a significant dispersion of conductivity with frequency, in agreement with the Cole-Cole relaxation function for pure PLZT and with the Davidson function -Cole in the case of the doped system.4
On the other hand, K. Rama Rao et al found that tin-doped PZT showed a type of non-Debye relaxation process. An analysis using the Cole-Cole relaxation function revealed the contribution of the grain and the boundary in the conduction processes. Activation energy values suggested conduction by 19 ions.
Despite having been studied by different models and methods, the conductive processes in these materials are not supported by a complete consistent microscopic theory that specifies the influence of defects or dopants on their electrical response. Thus, the need to investigate the mechanisms that underlie the process of transport or diffusion of ions that can be used as a basis for further developing new materials with better properties for their application.
In this work, a study about the influence of Mn-doping on relaxor behavior of the conductive process for lead lanthanum zirconate titanate ceramics is carried out.
Experimental procedures
PLZT powders with nominal composition Pb0,91La0,09(Zr0,65,Ti0,35)O3 were prepared by the traditional ceramic method.20) The precursor oxides, of high purity (Aldrich, >99 %), PbO, La2O3 , ZrO2 and TiO2 according to the desired stoichiometry, were mixed in a ball mill in a moist medium with distilled water for 20 hours. The deposition was dried and calcined in an alumina container at 850 °C for 3,5 hours, in a Liyi muffle (LY-XD). The ceramic bodies were subsequently formed by isostatic pressure and sintered at 1250 °C for 5 hours, at a heating rate of 5 °C/min.
The sintering of the samples was carried out in an atmosphere rich in lead oxide (PbO) to replenish the Pb that leaves the structure and the corresponding formation of vacancies in the crystallographic site B of the material. Amounts of MnO of 1, 2 and 3 % by weight were added to the PLZT powders, so that the PLZT + xMn compounds were obtained, with x= 0,0; 1,0; 2,0 and 3,0. The resulting powders were mixed again in a ball mill for 20 hours. Then proceeded the drying and calcination at a temperature of 850 °C for 3,5 hours. The calcined powders were then pressed at a pressure of 2,6 t/cm2. Finally, the pellets obtained (16 mm in diameter and 1 mm thick) were sintered at 1,200 °C for 60 min with a heating rate of 5 °C/min.
X-ray diffraction was performed on each system in an XPERT-PRO 2011 type diffractometer coupled to a Panalytical measurement system for the control of all measurement parameters and perform them automatically. The qualitative determination of the present phases in each sample was carried out using the Hanawalt method and the “Phase Identification from Powder Diffraction” Match! Program.
The dielectric response of PLZT was measured through the impedance spectroscopy method, using an Agilent E4980A Precision LCR Meter, in the range of 100 Hz to 10 MHz and 15 to 700 K of frequencies and temperature, respectively.
Results and discussion
Figure 1 shows the X-ray patterns corresponding to the structures of pure PLZT and doped PLZT with 1 % manganese (PLZT-1Mn), 2 % (PLZT-2Mn) and 3 % (PLZT-3Mn). In the pure PLZT sample (figure 1 a) an isostructural phase was found with the perovskite phase, in addition to a secondary pyrochlore phase of the Pb2La2O7 type, marked with the symbol (*).The presence of the pyrochlore phase in PLZT system is often associated to stoichiometry deviation or uncomplete perovskite growth during synthesis.8 The determination of the lattice parameters allowed identifying the crystal symmetry of PLZT as rhombohedral (R3c) according to the file 86136 of the Pearson's Crystal Data Library (PCD). In the case of PLZT system doped with manganese, figure 1 (b) , (c) and (d), no obvious changes to the XRD patterns or shift of the peaks of these ceramic samples were detected under different Mn-doping, which indicates that Mn ions have diffused into the PLZT lattices and that a small amount of Mn-doping will not change the crystal structure of the PLZT, because of the similar ionic radius of Mn ions and B-site ions.1
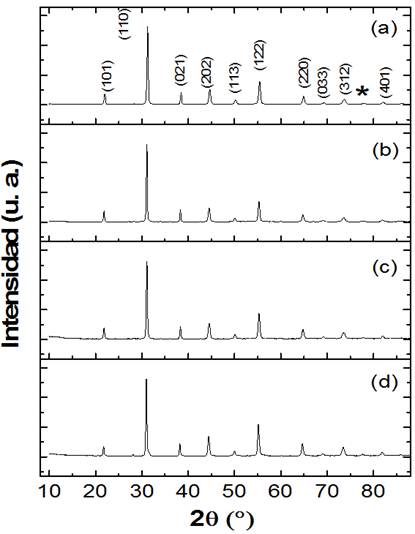
Fig. 1 X-ray diffraction pattern. PLZT (a), PLZT-1Mn (b), PLZT-2Mn(c), PLZT-3Mn (d). The symbol (*) corresponds to the reflection of the secondary phase Pb2La2O7
Figure 2 shows, for pure and doped PLZT (1 % as a representative case), the dependence of the real and imaginary parts (ε' and ε'') of the permittivity with the temperature at different frequencies. In the case of the pure system, both the real and imaginary parts of the permittivity show wide and well-defined peaks, as well as a marked dispersion with frequency, showing a typical behavior of a ferroelectric material with a diffuse phase transition and a relaxation character.1
In the case of the doped system, the dependency of the permittivity with the frequency is lost, and the relaxation character of the system is affected. This could be related to possible structural changes and defects caused by manganese occupying B sites in the crystal lattice to replace titanium (of different ionic radius), so modifying the degree of disorder of the structure. In addition, by compensation of charges, the emergence of oxygen vacancies can bring about the decrease of the movement of the domain walls in response to the applied electric field, which may disfavor the relaxation character of the system.
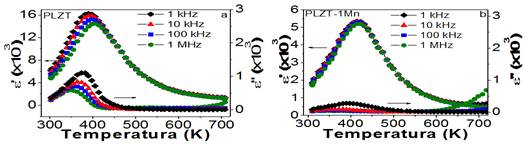
Fig. 2 Behavior of the real and imaginary parts of the permittivity with the temperature at different frequencies for pure PLZT (a) and doped at 1% (b)
However, at temperatures much greater than Tm, a dispersion of both the real and imaginary parts of the permittivity is verified, revealing the emergence of a relaxation mechanism, which, given the interval of temperatures in which it manifests, could be related to conductive processes.
In order to study the mechanisms involved in this process, in figure 3 the Logarithmic dependence of the real part of the permittivity with the frequency is shown, for PLZT-1Mn at different temperatures, in the range of 350 K to 430 K. Permittivity remains almost constant with the increase of frequency, this value corresponding to the static permittivity of the material. With the increase in temperature up to 410 K there is an increase in the real part of the permittivity, which shows that the polarization of the medium increases with the increase in temperature, so that the thermal movement helps increasing the polarization when activating the oscillation modes that favor the displacement of the ions that form the crystalline structure.
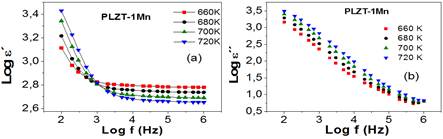
Fig. 3 Log-log plots of the real (a) and imaginary (b) dielectric permittivity as a function of de frequency.
For the temperature of 430 K there is a decrease of the real part of the permittivity. The cause of this is the ferro-paraelectric phase transition that takes place around 416 K.
The logarithmic dependence of the real part of the permittivity with the frequency begins to manifest, approximately, from 650 K. Figure 4 (left) shows, for PLZT-1Mn, the dependence of the real part of the permittivity with the frequency for different temperatures, in the range of 660 to 720 K.
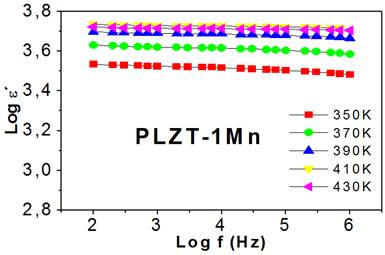
Fig. 4 Logarithmic dependence of the real and imaginary parts of the permittivity with the frequency for different temperatures
The real part of permittivity decreases considerably with the increase in frequency, but only in the range between 102 and 104 Hz. From 104 Hz the real part of permittivity remains approximately constant with the increase in frequency and its value decreases with the increase in temperature. This behavior is due to the fact that dipoles cannot follow the rapid variation of the field and the influence of thermal movement begins to play a more important role in the electrical properties of the system. This is in good agreement with what is observed in figure 2b, where it is verified that the dependence of the permittivity with the frequency for high temperatures is more evident for low frequencies. A similar behavior is observed for the samples doped at 2 and 3 %.
The behavior of the dielectric losses with the frequency for the PLZT-1Mn, as a representative case, is shown in figure 4 (right) at high temperatures. An approximately linear behavior with negative slopes is observed, which corresponds to a conductive process.4 With the increase in temperature, at the same frequency, the losses are increasing for each of the samples.
In this case, each of the curves tends to converge approximately at 5 · 105 Hz, a value from which there is a tendency to behave independently of the frequency.
Taking into account the marked dispersion of the real and imaginary parts of permittivity with frequency, it can be stated that a conduction process by ion jumps takes place.4) Conductive processes are usually studied in the impedance formalism, if the material is a conductor or in the dielectric module if the material is a dielectric with ionic conduction. Figure 5 (left) shows the dependence of the imaginary part of the electric module with the frequency for a temperature of 690 K for each of the ceramics under study.
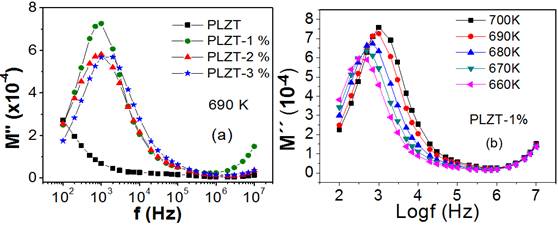
Fig. 5 Frequency dependence of the imaginary component of the dielectric modulus (a) for non-doped and Mn-doped PLZT ceramics and frequency dependence of the imaginary component of the dielectric modulus (b) for PLZT-1 % at different temperatures
In the frequency range considered, a peak of the imaginary part of the electrical module for the pure PLZT is not observed. This behavior, as seen in the graph, suggests that the conductive processes in this material take place at temperatures above 690 K and that in this temperature range it manifests at frequencies below 100 Hz. However, in the case of doped systems, a well-defined peak appears, showing the existence of a conductivity mechanism.
In order to study the dynamics of the relaxation of charge carriers, taking as a representative case the PLZT-1Mn, figure 5 (right) shows the behavior of the imaginary part of the electric module as a function of frequency, for different temperatures. In all cases well-defined peaks are observed in addition to an evident displacement of the maximum of the imaginary part of the module towards higher values of frequency, as the temperature increases, which is characteristic of a relaxation process.
To find the dependence of the relaxation parameters with temperature, in the samples doped at 1, 2 and 3 %, the relaxation distribution functions Cole-Cole (1), Davidson-Cole (2) and Havriliak-Negami (3) were used.
The best fit was achieved for the Cole-Cole function. In all cases, the correlation factor was around 0,99. As a fundamental parameter of these adjustments, we have the relaxation time (τ), characteristic of the process. The variation of this parameter with temperature corroborates that the process of relaxation by conductivity is a thermally activated process.
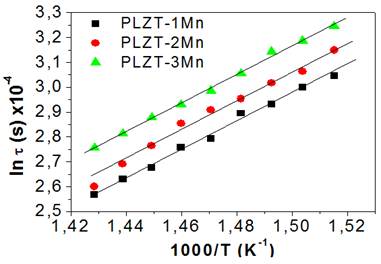
Figure 6 shows the behavior of the natural logarithm of the relaxation time versus the inverse of the temperature for PLZT-1Mn. The decrease of relaxation times with temperature is related to the fact that with the increase of thermal movement there must be an increase in the efficiency of the energy exchange between the ions and the structure and consequently a tendency to reach equilibrium faster. The activation energy that modulates the conductivity phenomenon can be determined through the gradient of the line. In a similar way, the procedure for calculating the activation energy is repeated in the case of PLZT-2 Mn and PLZT-3 Mn.
Table 1 shows these values. The similarity of the activation energies indicates that the conductive mechanism for doping at 1, 2 and 3 % is the same, that is, conductivity by ion movement. This is related to the entry of manganese into the system and the creation of oxygen vacancies to maintain the neutrality of the electric charge.
Conclusions
The PLZT system doped with the manganese cation at 1, 2 and 3 % was obtained and characterized. A ferro-paraelectric phase transition and a marked relaxation character for the PLZT ceramic is confirmed. In the case of the doped samples, a single Tm value is observed, inhibiting the relaxation character of the system. The presence of manganese in the initial ceramic generates a mechanism of relaxation by conductivity whose dynamics in the frequency domain responds to the Cole-Cole function, thus determining the relaxation times, typical of this process. It was also found the activation energy that modulates this process revealing conductivity by ion movement, which is related to the incorporation of manganese to the system and the creation of oxygen vacancies.