ARTICULO ORIGINAL

 

Método aproximado para la estimación de la temperatura en el centro de un producto de configuración cilíndrica

 

Approximate Method for the estimate of the Temperature in the Center of a Product of Cylindrical Configuration

 

 

MSc. José Gandón-Hernández^I, Ing. José E. Gandón-García^II

I: Facultad de Ingeniería Química. Instituto Superior Politécnico José Antonio Echeverría. CUJAE, La Habana, Cuba. [e-mail]
II: Instituto Superior de Diseño. La Habana, Cuba

 

 

---

Resumen

Como es sabido en el tratamiento térmico de los productos alimenticios, existe un punto o región en el interior de los mismos, conocido como centro térmico o punto crítico, donde los microorganismos tienen una mayor probabilidad de sobrevivir. La efectividad del procedimiento depende tanto de la temperatura como del tiempo necesario para alcanzar el valor letal requerido en el proceso. Desde el punto de vista de la transferencia de calor se trata un caso de conducción en estado no estacionario y sobre este aspecto aparece mucha información en la literatura técnica. En las soluciones gráficas y analíticas están presentes dos grupos adimensionales, el número de Fourier y número de Biot, este último está en función del coeficiente convectivo de transferencia de calor del medio de calentamiento o enfriamiento que rodea al producto. Encontrar un valor confiable de este coeficiente no es una tarea simple ya que además de depender de la densidad, la conductividad térmica, la viscosidad y la capacidad térmica específica, depende de la geometría y de las condiciones del flujo externo. En este trabajo se presenta un método, que mediante dos algoritmos relativamente simples permiten estimar, el valor del coeficiente de transferencia de calor para determinadas condiciones de trabajo y la temperatura en el centro térmico para un tiempo dado. Los cálculos se realizan mediante un programa de computación, diseñado e implementado al efecto, denominado CAENTER. La efectividad del método y las ventajas del programa se corroboraron con diferentes situaciones prácticas.

Palabras clave: centro térmico, conducción del calor, estado no estacionario, tratamiento térmico.

---

Abstract

In the heat treatment of the foodstuffs, exists one point or region in the inside of the same, known as thermic center or critical point, where microorganisms have a bigger probability of surviving. The effectiveness of the procedure depends so much of the temperature seemingly as of the necessary time to attain the lethal value required in the process. A case has to do with conduction not stationary from the point of view of the transference of heat and on this aspect; a lot of information in the technical literature appears. Two adimensional groups are present in the graphic and analytical solutions, Fourier and Biot numbers, this last depend of convection coefficient of the midway of heating or cooling that surrounds the product. To find a reliable value of this coefficient is not a simple task right now than in addition to depend on density, the thermic conductivity, viscosity and specific heat, depends on geometry and of the conditions of the external flow. A method, that by means of two relatively simple algorithms they allow estimating, presents the value of the heat transfer coefficient of heat for determined conditions of work and the temperature in the thermic center for a given time itself in this work. The calculations come true by means of a program of computation, designed and implemented for the purpose, named CAENTER. The effectiveness of the method and the advantages of the program ware corroborated themselves with different practical situations.

Keywords: center point, heat conduction, unsteady state, heat treatment.

---

 

 

INTRODUCCION

El tratamiento térmico es un proceso tecnológico donde se relaciona fundamentalmente la temperatura y el tiempo de procesamiento, en el caso de la metalurgia permite establecer los cambios necesarios en la estructura y las propiedades de una aleación, en la Industria Alimentaria su objetivo es evitar que se dañen los productos debido a la presencia de los microorganismos los cuales son susceptibles al efecto de calentamiento.

La configuración cilíndrica es muy frecuente en los alimentos térmicamente procesados y en estos existe un punto o región en el interior de los mismos, conocido como centro térmico o punto crítico, donde los microorganismos tienen una mayor probabilidad de sobrevivir. La efectividad del procedimiento térmico depende tanto de la temperatura como del tiempo necesario para alcanzar el valor letal requerido.

Existen otros procesos donde la relación entre la temperatura y el tiempo es objeto de un control estricto. Desde el punto de vista de la transferencia de calor se trata un caso de conducción en estado no estacionario y sobre este aspecto aparece mucha información en la literatura técnica.

En las soluciones analíticas así como en gráficas aparecen dos grupos adimensionales principales, el número de Fourier y número de Biot, este último está en función del coeficiente convectivo de transferencia de calor del medio de calentamiento o enfriamiento que rodea al producto. Encontrar un valor confiable de este coeficiente no es una tarea simple ya que además de depender de la densidad, la conductividad térmica, la viscosidad la capacidad térmica específica, también depende de la geometría y de las condiciones del flujo externo.

 

FUNDAMENTACION TEORICA

En este trabajo se presenta un algoritmo de cálculo mediante el cual se pueden estimar:

El valor del coeficiente de transferencia de calor para determinadas condiciones de trabajo.

La temperatura en el centro térmico para un tiempo dado.

Se presentan estas dos alternativas o variantes ya que si no se tiene un valor confiable del coeficiente de transferencia de calor cualquier inferencia del tiempo o la temperatura de procesamiento puede ser peligrosa.

Las "estimaciones experimentales" se pueden obtener mediante los valores de la temperatura y el tiempo en procesos industriales o a nivel de laboratorio, calcular el Bi y de este el valor del coeficiente. Una vez obtenido este valor se puede utilizar para todas aquellas determinaciones donde se cumplan con las condiciones operacionales y geométricas del "experimento".

Conocido el valor experimental o práctico del coeficiente de transferencia de calor entonces la determinación de la temperatura se convierte en el caso clásico que aparece en los textos.

El algoritmo se basa en la solución de la ecuación diferencial que describe la conducción del calor en estado no estacionario en un cilindro [3].

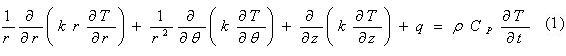
Esta ecuación, simplificada para las condiciones más adecuadas para el proceso de cocción de productos alimenticios con configuración cilíndrica, sin generación interna de calor y transferencia en dos direcciones, se puede expresar como:

En la teoría de la transferencia de calor en estado no estacionario, la solución de esta ecuación se presenta de diferentes maneras, las cuales han transitado desde la confección y la utilización de gráficos hasta el uso de programas computacionales basados en el uso del método de los elementos finitos.

En cualquiera de estas soluciones se emplean tres grupos adimensionales característicos, los que se definen de la siguiente forma:

Como se expresa en la introducción, de todas las variables que intervienen en la definición de estos grupos, tales como el régimen el coeficiente de transferencia de calor resulta el más problemático, pues depende de muchos factores, de flujo, el patrón hidrodinámico del fluido que rodea al cuerpo, sus propiedades físicas y características geométricas, todo lo cual dificulta su estimación precisa y solamente en casos muy particulares se pueden hacer suposiciones en cuanto a su valor.

Esta dificultad ha provocado que en la mayoría de los procedimientos e investigaciones relacionados con el control de la calidad se deban realizar mediciones frecuentes y estudios experimentales para determinar los tiempos de cocción de los diferentes productos.

Precisamente en este último aspecto radica el fundamento de este trabajo, pues si se dispone de datos experimentales para un proceso dado se puede estimar el valor del coeficiente de transferencia de calor sin recurrir al uso de las expresiones reportadas para la convección libre, las cuales en la mayoría de los casos no se ajustan a las condiciones del proceso de transferencia de calor que se desarrolla durante el tratamiento térmico.

Se infiere entonces que si se dispone de un valor experimental del coeficiente de transferencia de calor y las condiciones hidrodinámicas, el tipo de fluido y las características geométricas del sistema son similares; se puede utilizar este coeficiente para la estimación de tiempos y temperaturas de cocción.

 

METODOS UTILIZADOS Y CONDICIONES EXPERIMENTALES

Los cálculos se realizan mediante el CAENTER un programa de computación, diseñado e implementado por los autores en Visual Basic 6 para Windows desde XP hasta 10 y tiene  como requerimientos 128 MB de RAM y un espacio libre en disco de 10MB.

Como fue expresado, el programa se fundamenta en la solución de la ecuación diferencial, utilizando el parámetro adimensional:

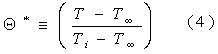
Para la solución de un problema de configuración cilíndrica con transferencia de calor con efectos multidimensionales se utiliza la combinación de las soluciones analíticas en las direcciones escogidas, en este caso z y r. Lo que implica la utilización de la ecuación que resuelve el caso del cuerpo plano de espesor 2L y el cilindro infinito.

Para el plano la solución exacta toma la siguiente forma:

Y los valores discretos, auto valores, de ζn son las raíces positivas de la ecuación transcendental.

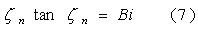
Cuando Fo ≥ 0,2 la solución de la serie infinita se puede aproximar al primer término de la misma, teniendo en cuenta esta simplificación la expresión de la solución adopta la siguiente forma:

La solución exacta para el cilindro infinito es:

Tanto J₁ como J₀ son las funciones Bessel de primera clase, las cuales aparecen tabuladas en diferentes textos y manuales así como las raíces de la ecuación transcendental [5].

Al igual que para el plano en este caso se utiliza la solución aproximada, considerando siempre Fo ≥ 0,2, por lo que la misma se puede expresar de la siguiente forma [2]:

Los valores de los coeficientes C1y ζ1 han sido determinados y están tabuladas en función del Bi en diferentes textos [5].

Teniendo en cuenta todas estas definiciones se puede llegar a una solución integral para el centro térmico de un cuerpo o producto de configuración cilíndrica.

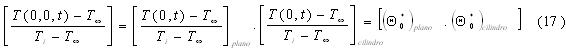
De aquí se puede obtener el valor de la temperatura en el centro térmico del cuerpo o producto.

Procedimiento de trabajo

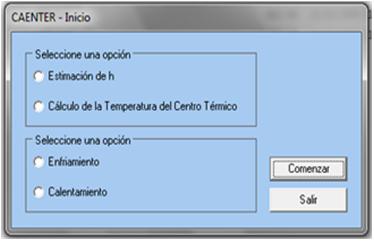
Se selecciona la opción requerida, según se muestra en la figura 1.

Fig. 1 Pantalla de inicio.

Para la estimación del coeficiente de transferencia de calor se debe suministrar la información mostrada en la figura 2 y figura 3.

Fig. 2 Estimación de h.

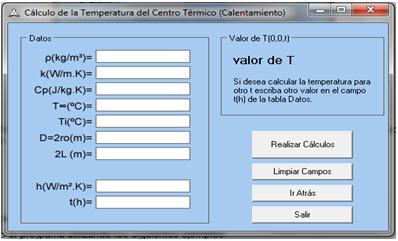
Fig 3. Cálculo de la temperatura en el centro térmico.

La efectividad del método y las ventajas del programa se corroboraron mediante dos aplicaciones.

 

RESULTADOS Y DISCUSION

El método y el programa se validaron utilizando los siguientes casos

Morcilla de arroz

Fuente	T(h)	h(W/m2ºC)	Texp(ºC)	T(0,0,t)(ºC)
Pereira [2]	1,5	100	96,5	97,6
CAENTER	1,5	100	96,5	96,04

Jamón cocido

Fuente	T(h)	h(W/m2ºC)	Texp(ºC)	T(0,0,t)(ºC)
Bruselas [1]	3,45	-	71,20	-
CAENTER	3,45	220*	71,20	71,19

*Valor estimado para condiciones de proceso similares

Como puede apreciarse en el caso del producto estudiado por Pereira, el CAENTER se aproxima más al resultado experimental, esto se debe a que aunque el método propuesto es aproximado, se basa en la solución analítica de la ecuación diferencial.

Para el jamón cocido, sólo se dispone del resultado experimental y el programa proporciona el valor de h que prácticamente permite reproducir este resultado.

Cuando se dispone del coeficiente ya se puede estimar el tiempo de cocción o la temperatura en condiciones similares aunque cambie la composición del producto.

 

CONCLUSIONES

El método propuesto constituye una herramienta valiosa para la estimación de la temperatura en los procesos de tratamiento térmico, pues permite:

1. Proyectar procesos de tratamiento térmico partiendo de una base teórica y experimentalmente fundamentada.

2. Reconocer el papel determinante de las propiedades físicas de los medios vinculados con el proceso de la transferencia de calor.

3. Predecir las variaciones de los parámetros tiempo y temperatura cuando se producen cambios en la composición o formulación de los productos.

Estos atributos se ponen de manifiesto con marcada importancia en el caso de los productos alimenticios con configuración cilíndrica, sometidos a procesos de escaldado, horneado, etcétera.

 

NOMENCLATURA

 

BIBLIOGRAFIA

1. BRUSELAS, A., PÉREZ, B., PEÑA, J., GUERRA, M.A. GANDÓN J., "Estudio del tratamiento térmico de embutidos", La Industria Cárnica Latinoamericana. Argentina. Nº172. 2011. p. 62-67

2. HEISLER, M. P., "Temperature Charts for Induction and Constant Temperatura Heating", USA, 1947.p. 227-236

3. INCROPERA, F.P. y D. P. DEWITT. Fundamentos de transferencia de calor. p.226-248. 4 edición, Prentice Hall, Mexico, 1999.

4. PEREIRA, J. A., "Application unsteady - state heat transfer equations to portuguese traditional meat products from Monchique región". Portugal, 2000.

5. SCHNEIDER, P. J., "Conduction Heat Transfer", Addison-Wesley, Reading, USA, Nº 6. 1995. p.143-15.

 

 

Recibido: Septiembre 2016
Aprobado: Diciembre 2016

 

 

MSc. José Gandón-Hernández^I. Facultad de Ingeniería Química. Instituto Superior Politécnico José Antonio Echeverría. CUJAE, La Habana, Cuba. [e-mail]