Introducción
En el actual Plan de estudios E, en el segundo año de la carrera Ingeniería Química, se imparte la asignatura Fundamentos de Biotecnología, la cual es básica-específica y se ocupa del estudio de las enzimas, del metabolismo de las biomoléculas, así como de los microorganismos. El objetivo esencial que se persigue es que el estudiante a este nivel conozca el fundamento de la fermentación, vocablo muy empleado en la carrera en procesos industriales mediados por microorganismos (m.o.). Por lo que la asignatura propicia en los estudiantes una familiarización con los conocimientos básicos de Bioquímica y Microbiología, asignaturas que se impartían en el antiguo Plan de estudios. De esta forma, se consolidan los conocimientos fundamentales para el entendimiento de procesos industriales en los que se emplean m.o., dentro de los que se encuentran los procesos biotecnológicos y de ingeniería genética, de ahí el papel de la asignatura en el Plan de estudios.
Un tema de gran importancia en la asignatura, es el estudio de las enzimas, su cinética e inhibición, este constituye un nexo entre la parte estática de la Bioquímica (el estudio de las biomoléculas) y la parte dinámica (el estudio del metabolismo). Las enzimas son catalizadores biológicos y el estudio de su cinética es un aspecto de vital importancia en la carrera.
Para que el estudiante se apropie de este contenido, se imparte, entre otras formas de docencia, una clase práctica. Esta única clase práctica, si bien consolida lo recibido en conferencias, no es suficiente, pues como los estudiantes se tienen que enfrentar al graficado de curvas y procesamiento matemático de los datos, se consume gran cantidad de tiempo, quedando poco para un análisis y discusión más amplia de los resultados. Otra dificultad es que no se pueden poner ejercicios que impliquen gran volumen de datos porque se consumiría todo el tiempo sólo en el procesamiento y graficado de estos. Todas estas dificultades atentan contra el buen desempeño de los estudiantes en la clase práctica y la adecuada adquisición de los conocimientos de un tema tan importante.
Teniendo en cuenta lo anterior y el hecho de que una de las estrategias curriculares de la enseñanza superior cubana es la de computación, en la cual todas las asignaturas deben tener asociados programas computacionales, se plantea como objetivo de este trabajo: emplear el MatLab como asistente matemático en la resolución de los ejercicios de la clase práctica de cinética enzimática de la asignatura Fundamentos de Biotecnología, en el Plan E.
Fundamentación teórica
En el Plan de estudios E de la carrera Ingeniería Química 1 se imparte la asignatura Fundamentos de Biotecnología, para dotar a los futuros egresados del fundamento bioquímico de los procesos fermentativos, conocimientos estos que les permitirán operar en plantas en las que se llevan a cabo procesos mediados por microorganismos como en las industrias láctea y cervecera, por solo citar algunas. Además de poder adquirir los fundamentos para operar en otras plantas de corte biotecnológico.
La asignatura se imparte en cuatro formas de docencia: conferencias, clases prácticas, seminarios y laboratorios. 2 La clase práctica de cinética enzimática es la que guarda más relación con el contenido de cinética del crecimiento microbiano, que se imparte en la propia asignatura en el Plan E, así como con la cinética de las reacciones químicas, que se imparte en Química Física 2. En efecto, la cinética es una de las ramas de la química más tratadas en la Ingeniería Química, de ahí la importancia de un tratamiento adecuado del tema en la asignatura Fundamentos de Biotecnología.
En la mencionada actividad práctica se debe graficar varias veces para calcular, por método gráfico, parámetros como la Km (constante de Michaelis-Menten), la cual ofrece una medida de la afinidad de la enzima por un sustrato, por un coenzima; también se grafica para analizar el efecto que ejercen ciertos inhibidores sobre la actividad enzimática, en este caso no solo se calcula la Km, sino la Vmáx (velocidad máxima) y la Ki (constante del inhibidor, constante de disociación del complejo enzima-inhibidor). Antes de graficar, los estudiantes deben procesar los datos según un método descrito en el libro de texto, llamado representación de los dobles recíprocos o de Lineweaver-Burk, el cual hace una modificación a la ecuación básica de la cinética enzimática, la ecuación de Michaelis-Menten. 3,4
Como se aprecia, el procesado de los datos y el graficado de los mismos consume gran parte del tiempo de la actividad, quedando poco para el análisis de los resultados y para una ejercitación adecuada que incluya más ejercicios de esta temática, por lo que se propone emplear el MatLab como procesador matemático en la realización de estos ejercicios.
En un primer trabajo realizado por los autores 5 se vio que en la carrera de Ingeniería Química de la Universidad de Oriente no se emplea el MatLab, sin embargo en esta carrera y otras afines de varias universidades alrededor del mundo sí se emplea esta herramienta computacional. Se analizó un artículo de la Universidad de Valencia, 6 en el cual los autores proponen sea el MatLab el único programa a emplear en la carrera Ingeniería Química, este trabajo, muy bien fundamentado, presenta las ventajas que supone la anterior propuesta.
En el mencionado trabajo, 5 los autores exponen que el empleo del MatLab en clases prácticas permite no solo graficar ahorrando tiempo, sino desarrollar en los estudiantes la habilidad de algoritmizar. Se mostraron las bondades del MatLab como lenguaje de programación, mencionando entre otras, las siguientes: amplio soporte matemático, alta precisión, amplio soporte de funciones ya desarrolladas, magnífica ayuda y gráficas bidimensionales y tridimensionales de diferentes tipos.
Materiales y métodos
A continuación, se presentan dos de los ejercicios de la asignatura Fundamentos de Biotecnología, que se deben resolver en la clase práctica de cinética enzimática, estos han sido tomados de la bibliografía. 3
El ejercicio 1 es un caso sencillo de cálculo de Km por el método gráfico. El ejercicio 2 es más complejo pues se pide determinar el tipo de inhibición, para lo cual los estudiantes deben realizar dos curvas en una misma gráfica. Todo ello requiere no solo de tiempo para procesar y graficar los datos sino de tiempo para el análisis de los resultados.
Ejercicio 1: La transaminasa cataliza la reacción:
El fosfato de piridoxal (PP) actúa como coenzima en el proceso catalítico. Calcúlese la Km para el complejo apoenzima-coenzima a partir de los datos siguientes, obtenidos al variar la concentración de PP mientras que las concentraciones de glutamato y de oxalacetato y las demás condiciones, se mantuvieron constantes:
Ejercicio 2: A partir de los siguientes datos de una reacción enzimática determine:
El tipo de inhibición.
La Km del sustrato.
La Ki para el complejo enzima-inhibidor.
Resultados y discusión
En este acápite se presenta la forma en que, programando en MatLab, se resuelven los ejercicios planteados anteriormente.
Solución del Ejercicio 1:
Lo primero que debe hacer el estudiante para solucionar el ejercicio es graficar los datos, ¿cómo hacerlo empleando MatLab? El primer paso es entrar los datos creando las variables, correspondientes en este caso a la velocidad y la concentración, lo cual se hace creando los respectivos vectores siguiendo la sintaxis nombrevariable=[número1 número 2 … númeron] como se muestra a continuación, recordando que en MatLab debe usarse punto para separar la parte entera de la decimal y punto y coma si el usuario no desea ver la operación en pantalla.
En este ejercicio se definieron las variables Vel y concPP, para almacenar los valores de velocidad y concentración de fosfato de piridoxal, respectivamente.
Una vez definidas las variables, se hallan los inversos, lo cual se realiza empleando los siguientes operadores (./) como se muestra a continuación:
Ahora se procede a graficar empleando la instrucción plot según la siguiente sintaxis: plot(variableindependiente,variabledependiente,'estilodelgráfico').
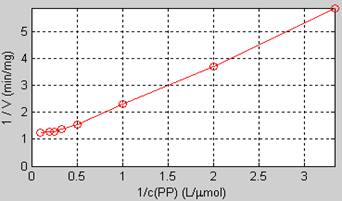
Luego de ejecutadas las instrucciones anteriores, se obtiene el gráfico mostrado en la figura 1.
Una vez obtenido el gráfico el estudiante debe interpretarlo y deducir que con los datos de la gráfica no puede determinar Km, pues esta se obtiene como el intercepto de la recta que se ajuste a los datos con el eje de las abscisas.
En MatLab para obtener dicha recta, óptima mediante mínimos cuadrados, y luego evaluarla, se emplean dos funciones: polyfit, que devuelve los coeficientes del polinomio óptimo, y polyval, que permite evaluar dicho polinomio.
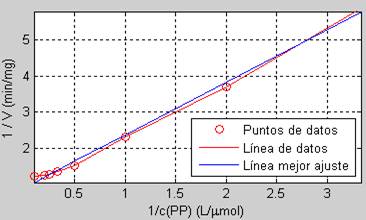
Lo anterior se logra mediante los siguientes códigos. Una vez ejecutados se obtiene la figura 2, en la cual se grafica la recta de mejor ajuste.
Para extrapolar la recta anterior hasta interceptar el eje de las abscisas se siguen las siguientes instrucciones, que luego de ejecutadas ofrecen la figura 3.
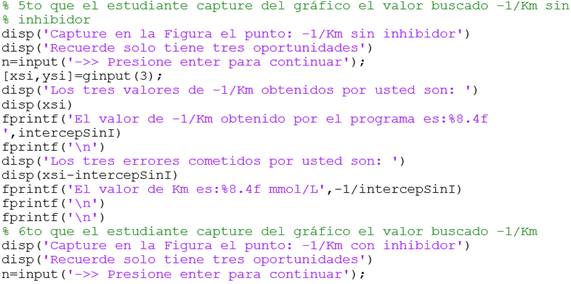
En este punto, con las siguientes líneas de códigos y el uso de la función ginput, el estudiante tiene la posibilidad de capturar tres valores del intercepto de la recta con el eje de las abscisas.
En la ventana de comandos del MatLab (Command Window) se comparan los resultados obtenidos por el estudiante con el calculado por el programa.
De esta forma se resuelve el ejercicio con la obtención de Km por el método gráfico, para el complejo apoenzima-coenzima. El estudiante debe interpretar el significado físico de este resultado atendiendo a sus unidades (µmol/L).
Solución del Ejercicio 2:
Como en el ejercicio anterior, el estudiante debe comenzar graficando los datos para lo cual puede crear un programa similar al anterior, quedando de la forma:
Luego de ejecutar estas instrucciones se obtiene el gráfico de la figura 4.
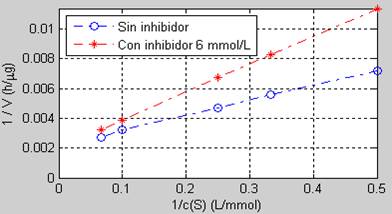
Fig. 4 Gráfica de la transformación de Lineweaver-Burk para los casos sin inhibidor y con inhibidor.
De modo semejante a lo realizado en el ejercicio 1, se emplean las funciones polyfit y polyval para obtener las rectas óptimas.
Luego de ejecutados los códigos anteriores se obtiene la figura 5.
A continuación, empleando los siguientes códigos se obtiene el gráfico, figura 6, que muestra las extrapolaciones de las rectas de mejor ajuste.
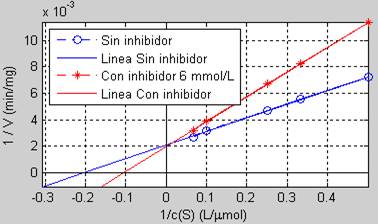
Fig. 6 Gráfica que muestra las extrapolaciones de las líneas de mejor ajuste para el cálculo de Km sin y con inhibidor.
En este punto, con las siguientes líneas de códigos y el uso de la función ginput, el estudiante, tal como en el ejercicio anterior, tiene la posibilidad de capturar tres valores del intercepto de cada recta con el eje de las abscisas.
En la ventana de comandos del MatLab se comparan los resultados obtenidos por el estudiante con los calculados por el programa, tal como se procedió en el ejercicio 1.
Al igual que en el ejercicio anterior, el estudiante debe ser capaz de llevar a cabo el análisis dimensional e interpretar los resultados de la Km. Además, debe llegar a la conclusión, partiendo de la gráfica correspondiente a la figura 6, que se trata de un inhibidor competitivo. Tiene que comparar los valores de Km en presencia y ausencia de inhibidor y con estos datos calcular el valor de la Ki, dándole respuesta al ejercicio.
Una forma similar de programación puede ser llevada a cabo para resolver en MatLab ejercicios que impliquen la inhibición no competitiva y acompetitiva.
De todo lo anterior se puede apreciar que, teniendo un primer ejercicio programado, el estudiante solo tendría que adecuar el resto de los ejercicios a la problemática en particular, por cuanto las formas de preguntar son semejantes.
De aplicar la propuesta que se hace en este trabajo, cambiaría el diseño de las clases prácticas, pues hasta la fecha solo se realiza una única clase práctica de cinética enzimática y con la propuesta se podría realizar una segunda clase práctica en el laboratorio de computación y orientar otros ejercicios en un trabajo extraclase que también requerirían de la programación para su solución.
Las ventajas que se obtendrían de emplear el MatLab en la solución de los ejercicios de cinética enzimática son las mismas que se presentaron en el trabajo previo realizado por los autores, en el que se aplicó el MatLab en algunas clases prácticas de Microbiología. 5 No obstante, a continuación se exponen tres de las ventajas más relevantes, aplicables a otras asignaturas de la carrera:
Las clases prácticas pudieran incluir más ejercicios del mismo tipo, ya que con la ayuda del procesador computacional se aumentaría la velocidad de resolución de los ejercicios. Esto se traduce en una mayor ejercitación del tema y mayor adquisición de los conocimientos por parte de los estudiantes.
Se emplea otro lenguaje de programación, MatLab, el cual, hasta la actualidad no se emplea en la carrera.
Los estudiantes se apropian de la forma en la que se programa en el MatLab, lenguaje de programación nuevo para ellos, por lo que amplían su cultura y consolidan el método en que los ingenieros resuelven los problemas de la vida real, empleando herramientas matemáticas.
Con los ejemplos de aplicación del MatLab abordados en 5 y con el presente trabajo se propone una forma novedosa y diferente de realizar las clases prácticas, que puede ser extendida a otras asignaturas de la carrera en el nuevo Plan de Estudio E 1, el cual demanda mayor protagonismo del estudiante para que sea capaz de adquirir conocimientos en el menor tiempo posible. Se impone entonces, como trabajo futuro, realizar un tercer artículo en el cual se resuman las principales funciones que posee MatLab, aplicables a la resolución de problemas de las restantes asignaturas de la disciplina Fundamentos Químicos y Biológicos para el plan E: Química General, Análisis Químico y Química Física I y II.