ARTÍCULO ORIGINAL

 

Gestión eficiente de modelos digitales de elevación para su visualización 3D utilizando procesamiento multinúcleo

 

Efficient management of digital elevation models for 3D visualization using multicore processing

 

 

Gilberto Arias-Naranjo^1*, Liesner Acevedo-Martínez¹, Yusnier Valle-Martínez¹, Jorge Fuentes-Rodríguez¹, Claudio Zinggerling²

¹ Centro de Estudios de Matemática Computacional. Universidad de las Ciencias Informáticas, Carretera a San Antonio de los Baños, km 2 ½, Torrens, Boyeros, La Habana, Cuba. CP.: 19370. Correo-e: {liesner, yvm, jfuentes} @uci.cu
² Centro Internacional de Métodos Numéricos Aplicados a la Ingeniería. CIMNE - UPC. Universitat Politècnica de Catalunya, Barcelona, España. Correo-e:  [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

En el siguiente trabajo se describe un modelo para la visualización eficiente de superficies de terrenos en tres dimensiones, que aprovecha las potencialidades de cómputo de los procesadores multinúcleos actuales. Se realiza una división lógica del terreno en cuadrantes, los cuales son representados utilizando quadtrees restringidos. La carga de los gráficos es controlada mediante una triangulación adaptativa de la superficie y aprovechando las ventajas de diferentes niveles de detalle. La escena que se está visualizando se gestiona dinámicamente, lo que permite mantener solamente en memoria los datos asociados a aquellos cuadrantes que se están visualizando. Aquellos cuadrantes que no se visualizan son almacenados en memoria externa y se gestionan utilizando una estructura de datos que permite un acceso eficiente a los datos de los mismos.

Palabras clave: multinúcleo, quadtree restringido, triangulación multiresolución, visualización 3D

---

ABSTRACT

In this paper is described a model for efficient visualization of terrain surfaces in three dimensions, which exploits the computational potential of today multi-core processors. A logical division of the terrain in tiles is performed, those tiles are represented using restricted quadtrees. The graphics load is controlled by an adaptive triangulation surface and taking advantage of different levels of detail. The scene being viewed is dynamically managed, keeping in memory only the data associated with those tiles that are being viewed. Those tiles that are not displayed are stored in external memory and managed using a data structure that allows efficient access to the data.

Key words: 3D visualization, multi-core, multi-resolution triangulation, restricted quadtree

---

 

 

INTRODUCCIÓN

La visualización interactiva de superficies de terrenos ha sido uno de los temas más estudiados en los últimos años en la disciplina Gráficos por Computadora. El incremento constante de las capacidades de almacenamiento en los sistemas de cómputo, así como el perfeccionamiento de las técnicas de adquisición de datos de la superficie terrestre, ha permitido crear grandes volúmenes de información de superficies de terrenos que requieren de gran eficiencia en las técnicas a utilizar para su visualización en tiempo real en entornos tridimensionales. El desarrollo gradual de la tecnología, que involucra el vertiginoso crecimiento en las capacidades de cálculo y almacenamiento de las Unidades de Procesamiento Gráfico (GPU), ha posibilitado representar estos datos interactivamente mediante modelos poligonales con diversos niveles de resolución.

Por consiguiente, los problemas en esta rama del conocimiento para la visualización de grandes superficies de terreno, están enmarcados fundamentalmente en la representación eficiente y la gestión de la información a representar. Una forma de elevar el desempeño de la representación es disminuyendo la complejidad de las geometrías que se utilizan para construir la escena. Sin embargo, esta reducción no puede comprometer la calidad de la superficie que estamos representando. Es por ello que esta simplificación puede ser controlada por un umbral de error, que es calculado utilizando determinadas métricas. Otra forma de controlar la complejidad de la representación es haciendo uso del concepto de niveles de detalle (LOD). Este concepto hace una analogía al sistema visual de las personas, donde los objetos aparecen a diferentes niveles de detalles, en función de la distancia y/o el ángulo de visión en que se encuentren. Por tanto, en vez de representar todos los elementos al mismo nivel de detalle, las partes de la escena se irán representando a menores resoluciones (con mayores umbrales de error) a medida que se vayan alejando del punto y la dirección en que se está mirando.

Otro elemento importante a tener en cuenta es que no siempre podremos tener toda la información de la superficie a visualizar en memoria interna. Para ello es necesario contar con un mecanismo que permita la administración dinámica de la escena que se está visualizando, cargando y descargando los elementos necesarios para que la visualización mantenga la calidad y la fluidez en la representación.

El presente trabajo aborda el problema de la visualización interactiva y en tiempo real con diferentes niveles de detalles de superficies de terreno que, por su extensión, no pueden ser representados completamente en memoria. La principal contribución se enfoca en el uso de quadtrees restringidos como estructura de datos espacial, para gestionar de manera eficiente grandes mallas poligonales como vía para la representación de esta clase de superficies y la definición de un esquema paralelo para la construcción de los quadtrees.

Trabajos anteriores

El problema de la simplificación de mallas y la triangulación multiresolución de superficies ha sido ampliamente estudiado por la comunidad científica en las últimas dos décadas. Un significativo número de variantes de solución se basan en el principio de triangulación de Delaunay (Kreveld, 1997) para crear TIN sobre conjuntos de puntos esparcidos irregularmente en el plano – ver además (de Floriani et al., 1996). Otra importante contribución en ese aspecto lo constituye la propuesta de (Hoppe, 1996), en la que se introduce una representación progresiva de las mallas como nuevo esquema de almacenamiento y transmisión de triangulaciones.

Entre las estructuras de datos más utilizadas para representar modelos digitales de elevación (MDE) jerárquicamente a partir de mallas regulares se encuentran los árboles binarios de triángulos (bintree) (Evans et al., 2001) y los quadtrees (de Berg et al., 2000). Específicamente, el quadtree de regiones es ampliamente utilizado para representar este tipo de información (Samet, 1989a), puesto que divide recursiva y jerárquicamente las superficies en regiones regulares. Cada nodo interior contiene exactamente 4 nodos hijos, donde cada uno de ellos representa uno de los 4 cuadrantes en que es dividida recursivamente la región. La propuesta de los autores en (Evans et al., 2001) conocida como RTIN, de igual forma que en (Duchaineau et al., 1997) donde se propone manejar las triangulaciones generadas por la subdivisión recursiva de los triángulos por el punto medio de su hipotenusa mediante dos colas de prioridad – ver además (Lindstrom and Pascucci, 2002) – , se basa en la misma jerarquía bintree, pero enfocada concretamente en la representación eficiente de la jerarquía mediante secuencias de bits, así como en la eficiencia de los recorridos sobre la estructura para la búsqueda de vecinos.

Las principales contribuciones en lo que se conoce como Triangulaciones Quadtree Restringidas (RQT) se describen en (Lindstrom et al., 1996), donde se introduce el uso de grafos de dependencias entre vértices para evitar la aparición de grietas en las superficies multiresolución; y en (Pajarola, 1998), que usa las relaciones de dependencias presentadas en (Lindstrom et al., 1996) para generar triangulaciones mínimas sobre quadtrees de regiones implícitos construidos sobre grandes mallas regulares. Röttger y colaboradores en (Röttger et al., 1998) también proponen un enfoque basado en quadtrees, centrado fundamentalmente en la representación eficiente de la estructura de datos a partir de una matriz de ceros y unos. El costo total en memoria de la variante de solución propuesta en (Röttger et al., 1998)  es muy reducido debido a que, además de los valores de altura del MDE, datos de textura y valores de error, solo se necesita un byte de información adicional por cada punto en el MDE. Otras contribuciones importante en lo concerniente al costo de almacenamiento de los modelos lo constituyen las propuestas de los autores en (Samet, 1989b) y (Pérez et al., 2006), basadas en el uso de curvas de recorrido del espacio (Asano, 1997) para codificar los nodos de un quadtree de manera eficiente y compacta.

El desarrollo creciente en cuanto a potencia de cálculo y velocidades de comunicación que experimentan en la actualidad las GPU, tiene un impacto significativo en el diseño y desempeño de las técnicas de representación y visualización de MDE en 3D en tiempo real en nuestros días. Las propuestas de solución que hacen uso de la GPU actualmente están enfocadas principalmente en el rendering de fragmentos triangulares de superficies (denominados parches) calculados en etapas de pre-procesamiento y almacenados en su memoria caché. Los autores en (Schneider and Westermann, 2006) proponen un esquema de comunicación eficiente entre la CPU y la GPU para actualizar incrementalmente un conjunto de arreglos de vértices e índices almacenados en esta última, disminuyendo significativamente los requerimientos de ancho de banda de la solución. Estos parches de triángulos constituyen la unidad básica la propuesta de (Cignoni et al., 2003a), en la que se aproximan eficientemente una superficie mediante el uso de TIN previamente calculadas y representadas en un bintree. Este método fue mejorado significativamente por los autores en (Cignoni et al., 2003b) para soportar el rendering interactivo de planetas en tiempo real. Otras contribuciones significativas lo constituyen las presentadas en (Livny et al., 2009), que propone la representación de los parches mediante 4 tiles de triángulos que pueden ser con diferentes niveles de resolución, y 4 secuencias de triángulos para conectarlos entre sí; y a (Bösch et al., 2009), que combina el uso quadtrees con bintrees para representar bloques de terreno y parches de triángulos  y de forma sencilla hacer un uso eficiente de la GPU en la simplificación de  mallas poligonales con múltiples niveles de resolución.

 

MATERIALES Y MÉTODOS

Triangulación utilizando quadtrees restringidos

La triangulación mediante quadtrees restringidos es una triangulación jerárquica y adaptativa para superficies de terrenos, donde la información es representada mediante mallas regulares (Pajarola, 1998). Una malla regular es una matriz de puntos los cuales se encuentran distribuidos a distancias constantes por ambas dimensiones.

Una forma para representar un quadtree sobre una malla regular, es considerando la propia malla como un quadtree y estableciendo a cada punto su relación con la jerarquía que se construye implícitamente. Esta representación tiene como inconveniente que las mallas tienen que ser cuadradas y sus dimensiones tener la forma 2k+1. Sin embargo, hace que las operaciones para acceder a los elementos del quadtree sean de orden constante (O(1)) en términos de operaciones de máquina (Pajarola, 1998).

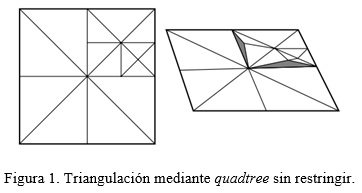
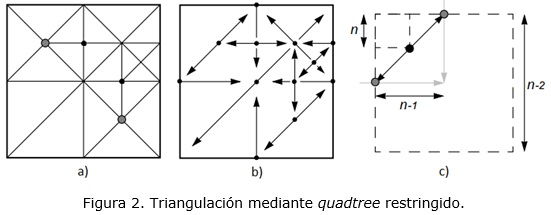
Para realizar la selección de los puntos que estarán incluidos en la triangulación se utiliza una métrica de error. Todo punto cuyo error esté por debajo de un umbral establecido, se considera no relevante para la triangulación y no es incluido en la misma. Sin embargo, si se sigue solamente este criterio, se puede llegar a triangulaciones donde existen grietas (ver figura 1). Para resolver este problema es necesario introducir una nueva restricción (Pajarola, 2002). Se establece entonces una relación de dependencia entre nodos del quadtree, cada vez que un nodo sea incluido en la triangulación (pues su error es superior al umbral establecido), sus dependencias también son incluidas (ver figura 2 a y b). Las dependencias de un nodo que es centro en su nivel son dos nodos centro del nivel inferior; las dependencias de un nodo no centro son los dos nodos centro de su nivel, adyacentes a él (ver figura 2 c).

El proceso de construcción del quadtree restringido y la triangulación están estrechamente relacionados. Como el quadtree estará implícitamente representado en la matriz de puntos, el problema consiste en determinar cuáles de ellos formarán parte de la triangulación. Se comienza por los nodos del último nivel y se van adicionando los puntos hasta llegar a aquellos en el nivel cero del árbol (los cuatro puntos en las esquinas de la matriz), siempre tomando como criterio base que el error aproximado del punto esté por encima del umbral establecido. Como las dependencias de un punto también son adicionadas, luego de seleccionado este según su error, esto implica que las dependencias de estos puntos también deberían ser adicionadas, lo que conlleva a un proceso concurrente.

Esta concurrencia trae como consecuencia que pueden ser visitados varios puntos en varias ocasiones (en función de cuantas veces fueron seleccionados puntos que tenían dependencias con ellos directa o indirectamente), haciendo que el algoritmo pudiese tener un comportamiento ineficiente a la hora de generar la triangulación. Como las dependencias de un punto no centro, son centros de su propio nivel, como las dependencias de un centro, son puntos del nivel inferior y como los puntos se van visitando desde el último nivel del árbol hasta el primero, entonces, si se recorren primero los puntos no centro y luego los puntos centro de cada nivel, se garantiza que todas las dependencias de los puntos seleccionados para la triangulación sean incluidas con solamente realizar una visita a cada punto de la matriz, teniendo el algoritmo una complejidad temporal lineal, en función de la cantidad de elementos que tiene la matriz que compone el quadtree (Pajarola, 1998).

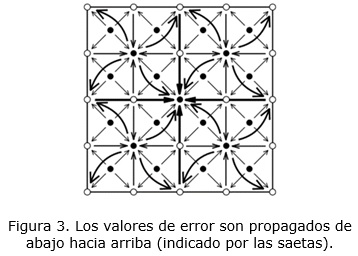
La métrica de error de espacio objeto utilizada está basada en la distancia euclidiana de un punto a un segmento. Cuando un punto es adicionado a una triangulación, es con el objetivo de incrementar el nivel de refinamiento de la misma y por tanto, divide uno o más triángulos en otros más pequeños. Como las mallas a representar son regulares, siempre el punto que se adiciona estaría encima de uno de los lados de los triángulos que divide (si se hace una proyección en dos dimensiones). Es por ello que el error que introduciría dicho punto, al ser incluido, estaría determinado por la distancia euclidiana desde él hasta el segmento que compone el lado del triángulo que divide. Considerando que al adicionar un punto también lo son sus dependencias y este proceso se va realizando de forma concurrente, entonces es necesario también considerar, para calcular el error aproximado de un punto, todos aquellos triángulos que fueron afectados tanto por él, como por sus dependencias. Por tanto todas las dependencias propagan su error al punto y el valor final del error aproximado es calculando tomando el valor máximo entre todos estos errores y el inducido por el propio punto (ver la figura 3) (Pajarola, 1998).

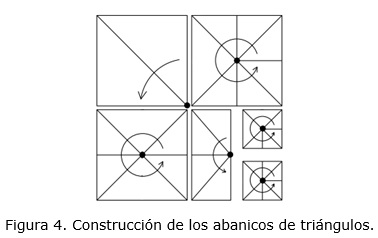
Un último paso importante es la extracción de la triangulación, luego de construida, para su futura visualización. La extracción de los triángulos utilizando abanicos es una de las variantes utilizadas para realizar este proceso. Se comienza utilizando el nodo centro del nivel uno y construyendo un abanico que contenga los cuatro cuadrantes en los que se divide el árbol en dicho nivel. Si uno de los cuadrantes se encuentra subdivido en cuadrantes más pequeños se desciende en la estructura y se construye otro abanico tomando como punto de referencia el centro de las cuatro regiones del cuadrante inicial. El proceso se realiza de forma recursiva hasta incluir todos los abanicos que representen completamente la triangulación (Röttger, y otros, 1998) (ver la figura 4). Los puntos que son comunes a varios abanicos deben ser repetidos en la construcción de estos lo que implica una alta redundancia de puntos en la creación de los abanicos. Sin embargo, cuando se hace una actualización de la triangulación provocada tanto por introducción como por la eliminación de puntos, solamente se afectan los abanicos que involucran los cambios realizados, dejando el resto invariables y evitando realizar todo el proceso de extracción nuevamente.

Gestión dinámica de la escena

Cuando se va a representar un terreno es necesario considerar tres elementos importantes:

• El terreno a representar puede ser tan grande que es imposible almacenarlo en memoria interna completamente.
• Las dimensiones de la malla regular no tienen por qué ser de la forma 2k+1.
• La malla regular no tiene por qué ser cuadrada.

Para resolver estos problemas se divide la malla que representa el terreno en cuadrantes (tiles) que tienen dimensión 2k+1. Los cuadrantes se almacenan en memoria externa y sólo son cargados en memoria interna aquellos que aparecerán en la escena que se está visualizando. Cada vez que un cuadrante, debido a movimientos de la escena, deje de visualizarse, se libera la memoria que ocupa para posibilitar la carga de nuevos cuadrantes. Estos cuadrantes son gestionados por una estructura espacial denominada FTTree la cual permite la representación de regiones donde las dimensiones no son de la forma 2k+1 (Martínez, 2012) (ver la figura 5).

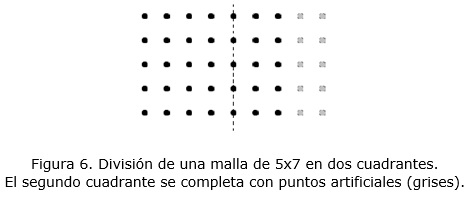
Los cuadrantes que se necesiten para la inclusión de los últimos puntos de la región se completan con puntos artificiales (ver la figura 6). Estos puntos adicionales, aunque garantizan que la estructura mantiene las características deseadas para la construcción del quadtree, no son contemplados luego en la visualización. Cada vez que ocurre un cambio significativo en la escena (traslaciones, aumento o disminución del nivel de detalle), se hace una consulta al FTTree para determinar qué cuadrantes necesitan ser cargados y cuáles liberados de la memoria interna de la computadora.

Para almacenar la información en memoria externa se tomó como base el diseño propuesto por (Lerbour, y otros, 2009). Los datos se organizan teniendo cada cuadrante por separado y almacenando los puntos ordenados por niveles del quadtree que se va a construir. En primer lugar se almacenan los cuatro puntos que componen el nivel cero del árbol, luego los del nivel uno y así sucesivamente, hasta completar todos los niveles. Esta forma de organización permite que al cargar un nuevo cuadrante en memoria puedan mostrarse triangulaciones parciales hasta que toda la información que se necesite, para el nivel de detalle que se estableció para el cuadrante, haya sido cargada. Como el error utilizado sólo necesita ser calculado una sola vez, este dato se almacena junto con el valor de altura de cada punto, evitando que sea necesario recalcular el error aproximado cada vez que es cargado un cuadrante.

LOD y mallado progresivo

Un elemento que impacta directamente en la representación eficiente del terreno es la utilización de diferentes niveles de detalle para representar los cuadrantes que están siendo visualizados en un momento determinado (Tianzi, 2009). Esto permite que cuadrantes que no están cerca del punto desde el que se está viendo la escena (punto de vista) se representen con un mayor umbral de error, lo que disminuye de forma drástica la cantidad de triángulos que son utilizados.

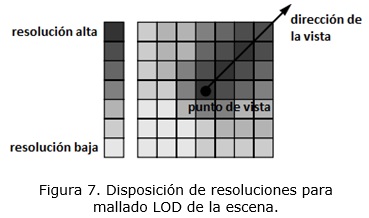
Partiendo de un umbral de error base, cada vez que se realiza una operación relevante sobre la escena, se recalcula el umbral específico de cada cuadrante, teniendo en cuenta dicho umbral base y la distancia a la que se encuentra el cuadrante del punto de vista (ver figura 7). En este caso, como las distancias se determinan desde el punto de vista hasta el cuadrante, consideramos que una operación es relevante sobre la escena cuando esta cambia el punto de vista de cuadrante (traslación) o cuando transforma la dirección en que se está mirando (rotación).

Como se mencionó anteriormente, la mayor parte de la información estará ubicada en la memoria externa y cada vez que sea necesaria su inclusión dentro de la escena es cargada para su procesamiento. Para lograr una visualización fluida se realiza la carga de cada quadtree comenzando por los nodos en el nivel cero y descendiendo en la jerarquía, incluyendo los puntos de forma paulatina. Ello conlleva a la necesidad de que las triangulaciones puedan variar sin tener que realizar el proceso completo nuevamente.

Otro elemento importante a considerar es que, aunque cada quadtree garantiza que los puntos que incluye construyen una triangulación continua, no se cumple lo mismo entre quadtrees que son adyacentes. Es necesario entonces, propagar los puntos frontera entre cuadrantes adyacentes para garantizar la continuidad del mallado (Tianzi, 2009).

El mallado progresivo consiste en realizar la actualización de la triangulación que se tiene adicionando o eliminando parte de los elementos (puntos, triángulos).

Esquema paralelo

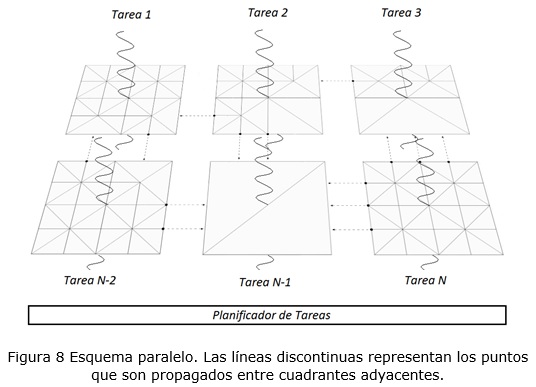
La división en cuadrantes del terreno es la fuente de paralelismo fundamental para plantear el esquema paralelo. En primera instancia la construcción de un quadtree restringido para un cuadrante es independiente del resto y por tanto se puede ejecutar de manera paralela. Cuando se trabaja, como es el caso, con mallado progresivo entonces se establece una dependencia de un cuadrante con sus vecinos. La dependencia está dada por lo puntos que es necesario propagar hacia los vecinos adyacentes para garantizar la continuidad del mallado (ver la figura 8).

Para la implementación paralela en C# se propone el uso de la biblioteca TPL(Acrónimo del inglés, Task Parallel Library que se traduce como biblioteca de tareas paralelas), incluida en la versión 4.0 de la plataforma .net. Esta biblioteca tiene la finalidad de facilitar el desarrollo de programas que exploten eficientemente las potencialidades de paralelización de los procesadores multinúcleos actuales.

TPL define un modelo basado en tareas (se refiere a algo que se quiere hacer frente al modelo clásico de paralelismo más orientado a la gestión de hilos) en lugar de los clásicos hilos. Los hilos son unidades de ejecución, el programador es responsable de crearlos, asignarles trabajo y manejar su existencia. En contraste el modelo que propone TPL es basado en unidades básicas de ejecución, las tareas. La biblioteca TPL ofrece el soporte para crear tareas y se encarga de gestionar su ejecución en hilos que ella misma maneja. Esto ofrece la posibilidad al programador de concentrarse en la creación de tareas que exploten las posibilidades de paralelización del programa y deja a TPL los detalles de planificación y ejecución de las mismas. El algoritmo de planificación que utiliza TPL es de tipo WorkStealing (Los algortimos WorkStealing tienen el propósito de lograr un balance de carga equilibrado entre las unidades de ejecución disponible. Basan su funcionamiento en dos conceptos: unidades de ejecución (hilos) y colas de tareas sirviendo a los hilos. Los hilos ejecutan las tareas extrayéndolas desde las colas FIFO,  si un hilo se queda sin tareas para ejecutar entonces intenta mantenerse ocupado robando una tarea del resto de las colas, de ahí el término Stealing).

La construcción del quadtree restringido para un cuadrante se define como una tarea de TPL, la ejecución de las mismas corre a cargo del planificador de TPL. La implementación del mecanismo de propagación de puntos se basa en la utilización de colas concurrentes. Las colas concurrentes sirven al mismo tiempo como mecanismos de sincronización entre las tareas. El propio procedimiento de construcción del quadtree define los puntos que son necesarios propagar hacia y desde las tareas vecinas utilizando las colas concurrentes.

 

RESULTADOS Y DISCUSIÓN

Implementación y experimentación

Para evaluar el desempeño en tiempo real del modelo presentado y compararlo con la variante secuencial se desarrolló un componente utilizando como interfaz gráfica OpenGL e implementado en el lenguaje C# sobre la plataforma .net 4.0 (ver la figura 9).

Fueron visualizadas varias superficies tomando como base modelos digitales de elevación con extensiones consideradas de tamaño pequeño (2k x 2k, alrededor de 4 millones de puntos) y mediano (4k x 4k, alrededor de 16 millones de puntos) y sobre una configuración de hardware con las siguientes características: CPU AMD Ahtlom II Dual-Core M300 a 2.0 GHz, 4 Gb de memoria RAM y una tarjeta de video integrada ATI Mobile Radeon HD 4200.

Se ejecutaron experimentos que consistieron en realizar un recorrido predeterminado por encima de las superficies, de forma tal que fuesen exploradas diferentes topologías de terreno (ejemplo: llanuras, montañas). En cada segundo fueron medidas la cantidad de cuadros generados por la variante secuencial (FPS_S), por la variante paralela (FPS_P) y la cantidad de miles de triángulos componiendo la imagen (MTpS). En la tabla 1 se presentan los resultados de las mediciones realizadas para muestras de diferentes modelos digitales de elevación, disponibles para su libre uso por la comunidad científica.

El estándar establecido para considerar que la visualización se está realizando en tiempo real es de al menos 70 cuadros por segundo. Como puede apreciarse, para datos de tamaño pequeño o mediano se obtiene un desempeño por encima de los 75 cuadros por segundo, superando en todos los casos la cota mínima recomendada. Otro resultado importante es que se logró aumentar la taza de cuadros representados en la versión paralela con respecto a la versión secuencial (17 cuadros por segundo como promedio). Cabe destacar que todo el procesamiento se está realizando en la CPU (no se explotan los recursos de cómputo de la GPU) y que la configuración de hardware presentada sólo permite la utilización de dos hilos de ejecución de forma simultánea.

 

CONCLUSIONES

El modelo presentado, además de hacer uso de las facilidades de procesamiento paralelo de las arquitecturas actuales, cumple con las principales especificaciones relacionadas en la bibliografía consultada: intercambio progresivo de elementos, triangulación en tiempo real, transiciones continúas entre varios niveles de detalle y almacenamiento y acceso eficientes en memoria externa. Sin embargo, es necesario continuar incorporando conocimientos de varias áreas como son gráficos por computadora, geometría computacional, sistemas de bases de datos, estructuras de datos espaciales y computación de alto rendimiento para arribar a soluciones mucho más eficientes.

OpenGL, a partir de su versión 3.1, incluyó funcionalidades que permiten el reinicio de primitivas. Esta facilidad permite la representación eficiente de abanicos de triángulos que sumado a la fácil actualización que se hace de los mismos cuando cambia la triangulación, hacen de los abanicos una variante atractiva a la hora de extraer las triangulaciones para su representación.

La utilización de un FTTree para administrar la escena permite representar mallas cuyas dimensiones no sean cuadradas sin embargo, los puntos artificiales adicionados requieren un tratamiento particular pues no pueden formar parte de la triangulación que se construya.

Aunque todo el procesamiento se hace en la CPU, los principios son extensibles y adaptables a soluciones que involucren la utilización de GPUs.

 

REFERENCIAS BIBLIOGRÁFICAS

ASANO, T., RANJAN, D., ROOS, T., WELZL, E., AND WIDMAYER, P. Space-filling curves and their use in the design of geometric data structures. Theoretical Computer Science, 181(1):3–15. 1997

BÖSCH, J, GOSWAMI, P, PAJAROLA, R. RASTeR: simple and efficient terrain rendering on the GPU. In Proceedings of the 30th annual conference of the European Association for Computer Graphics (EUROGRAPHICS 2009), Munich, Germany, pp. 35-42. 2009

CIGNONI, P., GANOVELLI, F., GOBBETTI, E., MARTON, F., PONCHIO, F., AND SCOPIGNO, R. Bdam – batched dynamic adaptive meshes for high performance terrain visualization. Computer Graphics Forum, 22(3):505–514. 2003a

CIGNONI, P., GANOVELLI, F., GOBBETTI, E., MARTON, F., PONCHIO, F., AND SCOPIGNO, R. Planet–sized batched dynamic adaptive meshes (p-bdam). In Proceedings IEEE Visualization, pages 147–155, Conference held in Seattle,WA, USA. IEEE Computer Society Press. 2003b

DE BERG, M., VAN KREVELD, M., OVERMARS, M., AND SCHWARZKOPF, O. Computational Geometry: Algorithms and Applications. Springer, 2 edition. 2000

DUCHAINEAU, M., WOLINSKY, M., SIGETI, D. E., MILLER, M. C., ALDRICH, C., AND MINEEV-WEINSTEIN, M. B. Roaming terrain: real-time optimally adapting meshes. In VIS ’97: Proceedings of the 8th conference on Visualization ’97, pp. 81–88, Los Alamitos, CA, USA. IEEE Computer Society Press. 1997

EVANS, W. S., KIRKPATRICK, D. G., AND TOWNSEND, G. Right-triangulated irregular networks. Algorithmica, 30(2):264–286. 2001

FLORIANI, L. D., MARZANO, P., AND PUPPO, E. Multi-resolution models for topographic surface description. The Visual Computer, 12(7):317–345. 1996

HOPPE, H. Progressive meshes. In SIGGRAPH ’96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pp. 99–108, New York, NY, USA. ACM. 1996

KREVELD, M. J. V. Algorithms for triangulated terrains. In SOFSEM ’97: Proceedings of the 24th Seminar on Current Trends in Theory and Practice of Informatics, pages 19–36, London, UK. Springer-Verlag. 1997

LERBOUR R, MARVIE J Y GAUTRON P. Adaptive streaming and rendering of large terrains: a generic solution. Proceedings of WSCG, 2009.

LINDSTROM, P. AND PASCUCCI, V. Terrain simplification simplified: A general framework for view-dependent out-of-core visualization. IEEE Transactions on Visualization and Computer Graphics, 8(3):239–254. 2002

LINDSTROM, P., KOLLER, D., RIBARSKY, W., HODGES, L. F., FAUST, N., AND TURNER, G. A. Real-time, continuous level of detail rendering of height fields. In SIGGRAPH ’96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pp. 109–118, New York, NY, USA. ACM. 1996

LIVNY, Y., KOGAN, Z., AND EL-SANA, J. Seamless patches for GPU-based terrain rendering. The Visual Computer, 25(3):197–208. 2009

MARTÍNEZ Y. Modelo de Representación de Superficies de Terreno para su Visualización en Tres Dimensiones. Ph.D. dissertation. Universidad de las Ciencias Informáticas, 2012.

PAJAROLA, R. Large scale terrain visualization using the restricted quadtree triangulation. In VIS ’98: Proceedings of the conference on Visualization ’98, pp. 19–26, Los Alamitos, CA, USA. IEEE Computer Society Press. 1998

PAJAROLA R. Overview of quadtree based terrain triangulation and visualization. Technical Report UCI-ICS TR 02-01. 2002.

PÉREZ, M., BENAVENT, X., AND OLANDA, R. Efficient coding of quadtree nodes. In Proceedings of the International Conference on Computational Science (3), volume 3993 of Lecture Notes in Computer Science, pp 13–16. Springer. 2006

RÖTTGER, S., HEIDRICH, W., SLUSSALLEK, P., AND SEIDEL, H.-P. Real-time generation of continuous levels of detail for height fields. In Proceedings of the 6th International Conference in Central Europe on Computer Graphics and Visualization, pp. 315–322. 1998

SAMET, H. The Design and Analysis of Spatial Data Structures. Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA. 1989a

SAMET, H. Applications of Spatial Data Structures: Computer graphics, image processing, and GIS. Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA. 1989b

SCHNEIDER, J. AND WESTERMANN, R. GPU-friendly high-quality terrain rendering. Journal of WSCG, 14
(1-3):49–56. 2006

TIANZI OUYANG. Terrain 3D Visualization based on Dynamic LOD Quadtree Arithmetic. Computer Development & Applications, 2009. Vol. 2.

XIAOWEI ZHENG et al. Multi-core paralle algorithms of the three-dimensional terrain model generation. Microcomputer & Its Applications, 2011. Vol. 8.

 

 

Recibido: 7/05/2014
Aceptado: 21/05/2014