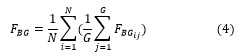Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.9 supl.1 La Habana 2015
ARTÍCULO ORIGINAL
Problemas de Optimización Decepcionantes Dinámicos, experimentación con Metaheurísticas
Deceptive Dynamic Optimization Problems, experimentation with Metaheuristics
Jenny Fajardo Calderín 1*, Claudia Cañedo Espino 1, Alejandro Rosete Suárez 1 ,Antonio Masegosa Arredondo 2, David A. Pelta 2
1 Instituto Superior Politécnico José Antonio Echeverría (CUJAE), Calle 114, # 11901, e/ Ciclovía y Rotonda, Marianao, La Habana, Cuba.
2 Grupo de Investigación en Modelos de Decisión y Optimización DECSAI, CITIC, Universidad de Granada, España.
*Autor para correspondencia: jfajardo@ceis.cujae.edu.cu
RESUMEN
Dentro del campo de la optimización existen una serie de problemas llamados NP, que son aquellos que pueden ser resueltos por un algoritmo no determinístico en un tiempo polinomial de resolución. Debido a que el mundo real no es estático, sino dinámico, se crea la necesidad de acercar dichos problemas de prueba a la realidad, de ahí que surgieran los problemas de optimización dinámicos (PODs). Uno de los problemas clásicos de optimización que existen, son los problemas decepcionantes o engañosos, que son problemas de prueba de generación binaria a partir de XOR. Son llamados engañosos porque a los algoritmos les cuesta mucho obtener mejoras, ya que cuando se mejora la solución con una heurística se empeora la evaluación en la función objetivo. En los últimos años ha habido un creciente interés por la modelación de los problemas dinámicos de optimización y su solución con los algoritmos metaheurísticos. Por ello, el objetivo de esta investigación es analizar el comportamiento de las metaheurísticas clásicas frente a los problemas decepcionantes dinámicos, específicamente con cinco funciones decepcionantes y evaluando el rendimiento de los algoritmos aplicando test estadísticos no paramétricos. Además se realiza una comparación de los resultados del mejor algoritmo con dos algoritmos del estado de arte para resolver problemas de optimización dinámicos: Adaptive Hill Climbing Memetic Algorithm y Self Organized Random Immigrants Genetic Algorithm.
Palabras clave: problemas de optimización dinámicos, decepcionantes, algoritmos metaheurísticas
ABSTRACT
In the optimization field there are a number of problems called NP, which are those that can be solved by a nondeterministic polynomial time algorithm for a resolution. Because the real world is not static, but dynamic, the need to bring these problems to test reality is created, hence arise dynamic optimization problems (PODs). One of the classic optimization problems that exist, are disappointing or deceptive problems, which are problems of test generation from binary XOR. They are called deceptive because the algorithms have a hard time getting improvements, because when solution is improved heuristic evaluation worsens the objective function. In recent years there has been an increasing interest in the modeling of dynamic optimization problems and their solution with metaheuristic algorithms. Therefore, the objective of this research is to analyze the behavior of the classical metaheuristics disappointing compared to dynamic problems, specifically with five disappointing functions and evaluating the performance of algorithms using non-parametric statistical test. Furthermore a comparison of the results of the best algorithm with two the state of art algorithms are usually done to solve dynamic optimization: Adaptive Hill Climbing Memetic Algorithm y Self Organized Random Immigrants Genetic Algorithm.
Keywords: dynamic optimization problems, deceptive, metaheuristics algorithm
INTRODUCCIÓN
La gestión, planificación y uso eficiente de los recursos, son aspectos claves para el desarrollo de una sociedad. En los modelos clásicos, elementos como los atributos de las tareas a planificar, las mercancías a distribuir, las características y condiciones del entorno físico, o cualquiera otro dato de entrada para los problemas que surgen en estas áreas, se asumían como perfectamente conocidos y estáticos. Sin embargo, en el mundo real, los problemas rara vez son estáticos, si no que algunos de sus atributos, costes, valores objetivo o restricciones pueden verse alterados con el transcurso del tiempo, dando lugar a la aparición de los problemas de optimización dinámicos (PODs) (Younes, 2006).
En los últimos años, ha habido una creciente investigación en la resolución de PODs. La aproximación dinámica a este tipo de problemas difiere del enfoque clásico en el sentido de que éste último se centra en condiciones estáticas e inmóviles, mientras que el enfoque dinámico admite que tanto el problema como sus soluciones evolucionen (cambien) con el tiempo. Desde el punto de vista de la optimización, el enfoque más básico para el dinamismo es simplemente reiniciar la búsqueda cada vez que se detecta un cambio, como si se tratara de un problema diferente. Sin embargo es ampliamente asumido por la comunidad científica que la evolución en el tiempo se produce de forma gradual, por lo que si cada cambio se tratara como un problema diferente implicaría la pérdida de la información adquirida hasta ese momento. La reutilización de información puede permitir una rápida adaptación al cambio, y además puede ayudar a encontrar mejores soluciones en menor tiempo. Esto es necesario en muchos casos prácticos, donde no hay tiempo para realizar exploraciones exhaustivas del espacio de búsqueda.
Entre los métodos propuestos para resolver PODs se encuentran: Algoritmos Evolutivos, métodos Multi-Swarm, Colonias de Hormigas y estrategias cooperativas. Una tendencia reciente en la resolución de POD es el uso de mecanismos de aprendizaje para adaptar la configuración del algoritmo (parámetros, operadores, etc.) durante la búsqueda. La razón principal de esta tendencia reside en la dificultad de encontrar una configuración adecuada para el algoritmo, siendo incluso más difícil que en los problemas estáticos (Amo, et-al, 2012; Cruz, Gonzalez, Pelta, 2011; Gonzalez, et-al, 2012). A pesar de esta dificultad, estudios como los anteriores muestran que existe una tendencia en utilizar el aprendizaje para resolver PODS, descartando las metaheurísticas clásicas, no se tienen en cuenta que todo depende del problema y los cambios que se pueden producir. Puesto que no se puede asegurar que existe un método que sea capaz de obtener los mejores resultados para cualquier problema de optimización, resultado conocido como Teorema “No Free Lunch” (Wolpert, 1996) que plantea: ningún algoritmo es superior a otro en la totalidad de los problemas en los que son aplicados.
Los problemas de optimización decepcionantes o engañosos son problemas de prueba de generación binaria a partir de XOR (Yang, 2013). Son llamados decepcionantes porque a los algoritmos metaheurísticos les cuesta mucho obtener mejoras, lo cual se debe a que cuando se mejora la solución obtenida con una heurística, se empeora la evaluación en la función objetivo, y la heurística que utilizan los algoritmos para guiar la búsqueda es la evaluación en la función objetivo.
Hasta la actualidad no se ha estudiado el comportamiento de los algoritmos metaheurísticos y la influencia de los parámetros frente a los problemas de optimización decepcionantes dinámicos. Por tal motivo, el objetivo de la presente investigación consiste en: evaluar el comportamiento de las metaheurísticas clásicas frente a los problemas decepcionantes dinámicos, profundizando el análisis sobre cinco funciones dinámicas. Se realizan experimentos con los algoritmos metaheurísticos: Escalador de Colinas, Limitado por Umbral, Recocido Simulado, Estrategia Evolutiva y Algoritmo Genético, y por último hacemos una comparación del algoritmo que mejores resultados obtiene con dos algoritmos del estado del arte para resolver PODs: Adaptive Hill Climbing Memetic Algorithm (Wang, 2009) y Self Organized Random Immigrants Genetic Algorithm (Yang, et-al, 2007).
Problemas de Optimización Dinámicos
La mayoría de los problemas de optimización del mundo real son inherentemente dinámicos. La optimización en entornos dinámicos enfrenta la solución de problemas que cambian en el tiempo y usualmente son definidos como problemas dinámicos. Estos problemas en los últimos años han sido protagonistas de variadas investigaciones, donde se definen como una secuencia de problemas estáticos enlazados por alguna regla dinámica (Branke, Schmeck, 2003; Cruz, Gonzalez, Pelta, 2011; Weicker, 2003 ).
Los investigadores han creado problemas que constituyen puntos de referencia para determinar el comportamiento de las metaheurísticas. El interés en el estudio de los PODs radica en su cercanía con los problemas del mundo real (predicciones meteorológicas, predicciones de mercado, control de movimientos robóticos, entre otros).
Un POD se define como ( Cruz, Gonzalez, Pelta, 2011):
![]()

En otras palabras, un POD es un problema donde la función objetivo y/o las restricciones cambian con el tiempo. El método más sencillo para resolver estos problemas es ignorar la dinámica, teniendo en cuenta cada cambio como la llegada de un nuevo problema de optimización, pero a menudo es poco práctico.
Los algoritmos que dan solución a problemas estáticos pueden encontrar una o más soluciones de buena calidad. En cambio, el objetivo de los métodos aplicados a los PODs ya no es el de localizar una solución óptima estacionaria, sino seguir la evolución de las buenas soluciones durante la ocurrencia de todos los cambios. Para esto, se necesitan métodos que permitan adaptar las soluciones en entornos que están en constante cambio ( Cruz, Gonzalez, Pelta, 2011).
Metaheurísticas para resolver PODs
La existencia de una gran cantidad y variedad de problemas difíciles, que aparecen en la práctica y que necesitan ser resueltos de forma eficiente, impulsó el desarrollo de procedimientos capaces de llegar a buenos estados o soluciones, aunque no fuesen óptimos. Estos métodos, en los que la rapidez del proceso es tan importante como la calidad de la solución obtenida, se denominan heurísticos o aproximados (brindan una solución específica). Las heurísticas están hechas a medida y diseñadas para resolver un problema y/o instancia específica, por lo cual surgen las metaheurísticas que son algoritmos de propósito general que se pueden aplicar para resolver cualquier problema de optimización (Doerner, 2007; Parejo, 2011).
Las metaheurísticas se pueden aplicar en diferentes contextos: aprendizaje automático, minería de datos, física, biología, logística, control y procesamiento de imágenes, entre otros. Se clasifican en dos grupos principales: basados en un punto o de trayectoria, y basados en poblaciones de puntos. Los métodos de búsqueda basados en un punto son aquellos que partiendo de un punto, buscan la vecindad y actualizan la solución actual en función de esta, formando una trayectoria, de punto a punto. Los algoritmos basados en poblaciones, trabajan con un conjunto de soluciones en cada iteración, y su resultado debe ser el mejor individuo de la población o sea el individuo mejor adaptado.
En el conjunto de los algoritmos poblacionales se encuentran los Algoritmos Evolutivos, los cuales comprenden una serie de técnicas que tienen sus bases en modelos biológicos, y están inspiradas en la teoría darwiniana de la evolución natural. Se basan en el intercambio de información entre los individuos de una población o de distintas poblaciones, características comunes, comportamiento social, etc. El intercambio se produce como resultado de aplicar el proceso de selección, competición y recombinación de los individuos. Desde el punto de vista biológico son algoritmos simples, y proporcionan mecanismos de búsqueda adaptativos ( Cruz, Gonzalez, Pelta, 2011; Doerner, 2007).
El planteamiento general es que en estos POD se trata de seguir un “óptimo móvil” y, por tanto, se asume que este seguimiento se puede realizar mejor utilizando un conjunto de optimizadores/soluciones/agentes, en lugar de un elemento de búsqueda aislado. Ejemplos de este enfoque utilizando los algoritmos evolutivos como técnicas de resolución. La evaluación de técnicas en este tipo de problemas no es trivial. En el año 2009 se organizó una competición: ECiDUE-Competition09, para evaluar el comportamiento de algoritmos en entornos dinámicos en el marco del CEC 2009, esta competición se repitió en 2012, en el marco de la misma conferencia. Estos han intentos interesante, pero aún la utilización de los “benchmarks” propuestos y las métricas de rendimiento, no son simples de implementar y adaptar a cualquier problema de optimización ( Branke, Schmeck, 2003; Cruz, Gonzalez, Pelta, 2011; Weicker, 2003 ).
Desde el punto de vista de la optimización, el enfoque más básico para el dinamismo es simplemente reiniciar la búsqueda cada vez que se detecta un cambio, como si se tratara de un problema diferente. Sin embargo, dado que la evolución en el tiempo por lo general se produce de forma gradual, hacer frente al cambio como si se tratara de un problema completamente nuevo implica que la información importante que se encontró en soluciones anteriores se pierde. La reutilización de esta información permite una rápida adaptación al cambio en el problema, lo que disminuye el tiempo necesario para encontrar una nueva solución. Esto es necesario en muchos casos prácticos, donde no hay tiempo para realizar exploraciones exhaustivas del espacio de búsqueda (Branke, Schmeck, 2003; Cruz, Gonzalez, Pelta, 2011; Doerner, 2007).
La mayor parte de las investigaciones hechas en problemas dinámicos se limitan al uso de algoritmos evolutivos, pero aún no hay ningún criterio claro de cuál es el mejor algoritmo a aplicar en cada caso o cómo afrontar un problema dinámico nuevo. Otro tipo de estrategias que han conseguido mejorar los resultados de los primeros algoritmos evolutivos son las estrategias cooperativas donde se vio incluso que los métodos de trayectoria podían obtener buenos resultados cuando formaban parte de una estrategia de este tipo ( Branke, Schmeck, 2003; Cruz, Gonzalez, Pelta, 2011; Doerner, 2007).
MATERIALES Y MÉTODOS
En el siguiente apartado se describe el marco de experimentación de la presente investigación, el cual comenta la métrica de rendimiento utilizada, los test estadísticos no paramétricos utilizados y la configuración de los parámetros utilizada. Además se comentan dos algoritmos del estado del arte que están diseñados para resolver PODs.
Medida de rendimiento
Se han desarrollado diferentes medidas de rendimiento para evaluar el comportamiento de los algoritmos metaheurísticos para resolver PODs. Las medidas de rendimiento son ampliamente utilizadas y pueden estar clasificadas en dos grupos principales: basadas en comportamiento y basadas en optimización. En este trabajo, la métrica que se utilizó para evaluar el comportamiento de los algoritmos Offline Performance, puesto que la mayoría de los trabajos más recientes en el tema de los PODs utilizan esta medida.
El Offline Performance fue creada por Branke y Schmeck en el año 2003 ( Branke, Schmeck, 2003; Cruz, Gonzalez, Pelta, 2011), mide el rendimiento offline para evaluar los algoritmos en caso de que no se conocen los valores exactos de los óptimos globales. Esta medida tiene dos desventajas, en primer lugar, se requiere que el momento en que se produce un cambio sea conocido y en segundo lugar, no son normalizadas y por lo tanto pueden estar sesgadas en ciertas circunstancias. Se define formalmente como:
donde N es el número de ejecuciones; en la definición original G es el número de generaciones (que se corresponde directamente cuando se trata de algoritmos evolutivos) y para este caso es el número total de iteraciones y es la evaluación de la mejor solución encontrada en cada iteración para cada ejecución.
Método de comparación: Test Estadísticos No Paramétricos
Diferentes autores han centrado su interés en test que sean adecuados para realizar un estudio comparativo entre algoritmos. En los test paramétricos los datos tienen una determinada distribución, se establecen afirmaciones sobre los parámetros de dicha distribución. En el caso de los test no paramétricos las afirmaciones establecidas no se hacen en base a la distribución de las observaciones, ya que a priori es desconocida. Para este trabajo los test que se ajustan al análisis son los no paramétricos.
Es interesante comparar los resultados de los algoritmos sobre un conjunto de configuraciones de uno o varios problemas para tener una visión más completa. En este sentido, García et al. (2009) proponen las directrices para llevar a cabo este análisis global usando pruebas estadísticas no paramétricas. Estas pruebas permiten clasificar el desempeño de dos o más métodos sobre un conjunto de problemas y configuraciones para determinar si las diferencias en el funcionamiento son significativas o no. El significado de las diferencias se evalúa mediante la comparación de estimadores (por lo general el valor de la media/mediana) del rendimiento de los algoritmos sobre cada configuración problema.
Los test no paramétricos por pares permiten, por ejemplo, determinar el mejor método global sobre todas las configuraciones de los problemas considerados en este trabajo. Se utilizó el test de Friedman para determinar si existe alguna diferencia significativa entre el rendimiento de dos o más métodos, y se utilizó el test de pares de Wilcoxon para evaluar si existe alguna diferencia significativa entre el rendimiento de dos algoritmos. Los test no paramétricos, específicos de este trabajo fueron aplicados usando el software estadístico SPSS.
Dado que los resultados para cada posible algoritmo, instancia, severidad y frecuencia de cambio, serían difícil de interpretar si se muestra como una tabla con valores numéricos, se utilizó un esquema de ranking (SRCS), propuesto en (Amo, 2012). SRCS utiliza test no paramétricos (Kruskal-Wallis y Mann-Whitney Wilcoxon con corrección de Holm’s para comparaciones múltiples) para evaluar la significación estadística de las diferencias individuales entre cada par de algoritmos en todas las configuraciones del problema. Si la prueba concluye que hay suficiente evidencia estadística de diferencia de rendimiento, el algoritmo con el mayor offline performance suma 1 a su ranking, y el otro suma −1. En caso de empate, ambos reciben un 0. El rango de los valores en el ranking de n algoritmos para cualquier problema es ![]() . Cuanto más alto sea el ranking obtenido, mejor se puede considerar un algoritmo en relación con los otros. A cada valor de ranking se asocia un color, utilizando blanco para el valor más alto del ranking
. Cuanto más alto sea el ranking obtenido, mejor se puede considerar un algoritmo en relación con los otros. A cada valor de ranking se asocia un color, utilizando blanco para el valor más alto del ranking ![]() y el valor más oscuro para el más bajo
y el valor más oscuro para el más bajo ![]() . Los colores para los valores intermedios se ajustan proporcionalmente.
. Los colores para los valores intermedios se ajustan proporcionalmente.
A partir de lo anterior dada una instancia del problema, se construye un ranking para cada variación de frecuencia y severidad. Si se agrupan las gráficas de un algoritmo para un problema dado con cada combinación de frecuencia y severidad posible, se puede obtener una matriz de color, donde es fácil observar cómo el algoritmo funciona para ese problema específico. El color blanco en una celda dada indica que el algoritmo es estadísticamente mejor que todos los otros algoritmos para la configuración de un problema específico. Si el color es más oscuro significa que el algoritmo es estadísticamente igual o peor que otros algoritmos para esa configuración del problema.
Configuración de parámetros de los algoritmos
En el diseño de los experimentos se realizó una configuración de parámetros para cada uno de los escenarios. Se utilizaron dos variables fundamentales con las cuales se le introduce dinamismo al problema, las cuales se muestran a continuación:
- Período de cambio: 1200, 3000, 6000, 9000, 12000 iteraciones.
- Severidad de cambio: 0.1, 0.2, 0.5, 0.9.
Para la comparación de los algoritmos se realizaron 30 ejecuciones independientes de cada uno de ellos, para 100 cambios de la función objetivo para cada configuración de problema, período y severidad.
Para la experimentación con los algoritmos metaheurísticos se utilizó la biblioteca de clases BiCIAM (Calderín, 2010) que contiene implementaciones en Java de versiones estándar de las metaheurísticas más comunes como: Escalador de Colinas de Primer Ascenso (EC), Búsqueda Aleatoria (BA), Recocido Simulado (RS), Limitado por Umbral (LU), Algoritmo Genético (AG) y Estrategia Evolutiva (EE). A continuación en la Tabla 2 se describe la configuración de parámetros utilizada para cada uno de los algoritmos comentados anteriormente.

Métodos del estado del arte
Adaptive Hill Climbing Memetic Algorithm (AHMA)
El AHMA propuesto por Wang (2009) fue diseñado originalmente para resolver PODs combinatorios. AHMA combina un algoritmo genético con una búsqueda local que utiliza dos operdores de acuerdo a una distribución de probabilidad que se ajusta durante la búsqueda. Los operadores que utiliza la búsqueda local son: Greedy Crossover Hill Climbing (GCHC) y Steepest Mutation Hill Climbing (SMHC). El GCHC aplica un operador de cruce a la solución élite y a otro individuo de la población actual que es seleccionado con el método de la ruleta. Se devuelve el mejor de los dos hijos obtenidos. El SMHC selecciona al azar un número de bits de la solución élite y los invierte. Al igual que en el operador anterior, si la solución resultante mejora a la élite entonces la reemplaza.
AHMA selecciona aleatoriamente uno de estos dos operadores de acuerdo con una distribución de probabilidad que se adapta a lo largo de la búsqueda, con el objetivo de dar una mayor probabilidad al operador que mejores resultados obtiene. El esquema de aprendizaje ajusta los valores de probabilidad en función del grado mejora que producen, cuando ocurre un cambio no se actualizan los valores por lo cual reutiliza la información aprendida. AHMA también incluye dos métodos para generar diversidad en la población actual: Adaptable Dual Mapping (ADM) y Triggered Random Immigrants (TRI).
Sel f Organized Random Immigrants Genetic Algorithm (SORIGA)
SORIGA (Sel f Organized Random Immigrants Genetic Algorithm) propuesto por Tinós and Yang (2007) es inspirado en el flujo de inmigrantes de una población. SORIGA trabaja con dos poblaciones: población principal y sub-población. Inicialmente se construye aleatoriamente la población principal, luego se divide en dos, combinando los individuos mejores adaptados con los menos adaptados, formando la subpoblación. Ambas poblaciones evolucionan, es decir se someten a un Algoritmo Genético: selección, cruzamiento y mutación. El cruzamiento es permitido solamente entre individuos de la misma población.
Existen diferentes estrategias de reemplazo en SORIGA, entre las más conocidas se encuentran: sustitución de individuos de la población principal elegidos al azar por los de la sub-población, o los individuos de la población principal con el menor fitness se sustituyen por individuos aleatorios. El flujo de inmigrantes generalmente aumenta el nivel de diversidad genética de una población, lo cual puede permitir escapar de óptimos locales.
RESULTADOS Y DISCUCIÓN
Inicialmente se realiza un análisis más detallado aplicando la técnica SRCS que se describió anteriormente que permite observar que ocurre para cada configuración concreta de los problemas, para los diferentes escenarios, con cada uno de los algoritmos. Se muestran los resultados con una matriz de dos niveles utilizando la técnica SRCS. En el nivel superior, las columnas se corresponden con los problemas, y las filas con los algoritmos. En un nivel más inferior de las columnas y filas se encuentran las configuraciones de frecuencia de cambio y severidad de cambio respectivamente. Por lo tanto, cada celda de estas matrices muestra el color obtenido por la técnica SRCS que corresponde al ranking de un algoritmo en una configuración del problema en específico. El nivel superior se corresponde con cuatro problemas en las columnas y cinco algoritmos en las filas, los resultados de un algoritmo en un problema con una configuración de severidad y frecuencia de cambio se ilustran en un cuadrado dentro de la matriz.
En la Figura 2 se muestran los resultados a partir del ranking que se obtiene con la técnica SRCS, se puede apreciar que el algoritmo con mejores resultados con diferencias significativas en la mayoría de los escenarios fue el Limitado por Umbral. Además se obtuvo que el algoritmo de peor rendimiento de forma general fue el Recocido Simulado, solo en la variante DeceptiveV3 el de peor rendimiento en todos los escenarios fue el Escalador de Colinas, y que el comportamiento del Algoritmo Genético y la Estrategia Evolutiva es muy similar en la mayoría de los casos.
Por último se realizó un análisis de los resultados del algoritmo de mejor rendimiento que fue el Limitado por Umbral con los algoritmos del estado del arte: AHMA y SORIGA. Se hizo un análisis global de los algoritmos con todas las instancias del problema y configuraciones mediante el test de Friedman. Los estadígrafos obtenidos se encuentran en la tabla 3 que muestra un ranking promedio de los algoritmos, donde el p-valor obtenido es: 0.00, por lo tanto se puede decir que hay diferencias significativas entre los datos y se rechaza la hipótesis nula del test.
Los árboles de descomposición permiten navegar a través de los diferentes niveles de información observando el aporte que realiza cada nivel al nivel anterior, permitiendo a los usuarios realizar consultas analíticas. En la figura 7 se puede observar el árbol descomposición del reporte que muestra los tiempos de permanencia de los empleados en la organización. Este árbol representa el tiempo de permanencia de los empleados que trabajan en el programa “Aplicaciones de Reconocimiento de Patrones”, en tres niveles de información programa, proyecto, y empleado.
CONCLUSIONES
En el presente trabajo se realiza un análisis del comportamiento de algunos de los algoritmos metaheurísticos clásicos frente al problema Deceptive, con cuatro variantes del problema y diferentes configuraciones de severidad y frecuencia de cambio. También se tuvieron en cuenta test estadísticos no paramétricos para evaluar el comportamiento, lo cual garantiza un correcto análisis.
Luego de desarrollar la presente investigación se puede concluir que los algoritmos metaheurísticos se utilizan para resolver PODs ya que garantizan encontrar una buena solución no necesariamente la óptima. Crear algoritmos capaces de adaptarse a los cambios en los PODs es un reto para la comunidad científica actual, ya que es desconocido que algoritmo es mejor en cada caso y cómo afrontar un problema dinámico nuevo. Sin embargo se deben tener cuenta algoritmos como el Limitado por Umbral que ha sido ignorado, demostró que puede obtener buenos resultados en los problemas. Además se obtuvo que el Limitado por Umbral tiene mejor rendimiento que dos de los algoritmos del estado del arte para resolver PODs, con diferencias significativas de forma global para todos los problemas y configuraciones. En términos generales, los resultados muestran que tiene sentido aplicar los algoritmos metaheurísticos clásicos a los PODs. Para futuras investigaciones está claro que se hace necesario un análisis más profundo comparando estos resultados con otros algoritmos del estado del arte que resuelven PODs.
AGRADECIMIENTOS
Este trabajo ha sido financiado por el Proyecto TIN2011-27696-C02-01 del Ministerio de Economía y Competitividad de España, P11-TIC-8001 del Gobierno de Andalusía (incluidos fondos FEDER de la Unión Europea).
REFERENCIAS BIBLIOGRÁFICAS
BERSON, A. & SMITH, S. J. 1997. Data Warehousing, Data Mining, and OLAP, McGraw-Hill, Inc.
BOUMAN, R. & VAN DONGEN, J. 2009. Pentaho Solutions: Business Intelligence and Data Warehousing with Pentaho and MySQL, Indianapolis, Indiana, Wiley Publishing, Inc.
CASTELLANOS, M., SIMITSIS, A., WILKINSON, K. & DAYAL, U. 2009. Automating the Loading of Business Process Data Warehouses. Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology. ACM.
CASTERS, M., BOUMAN, R. & VAN DONGEN, J. 2010. Pentaho Kettle Solutions: Building Open Source ETL Solutions with Pentaho Data Integration, Indianapolis, Indiana, Wiley Publishing, Inc.
DÍAZ, L., LÓPEZ, B., GONZÁLEZ, L., GALINDO, Y. & LÓPEZ, D. 2013. Integración de Datos. “Universidad Central “Marta Abreu” de las Villas”.
ECCLES, M. J. 2013. Pragmatic Development of Service Based Real-Time Change Data Capture. Aston University.
EL-SAPPAGH, S. H. A., HENDAWI, A. M. A. & EL BASTAWISSY, A. H. 2011. A proposed model for data warehouse ETL processes. Journal of King Saud University-Computer and Information Sciences, 23, 91-104.
GARCÍA, J. L. 2014. Automatización de los procesos de carga en el mercado de datos Recursos Humanos de la UCLV. Universidad Central “Marta Abreu” de Las Villas.
JÖRG, T. & DESSLOCH, S. 2008. Towards generating ETL processes for incremental loading. In: DESAI, B. C. (ed.) Proceedings of the 2008 international symposium on Database engineering & applications. Coimbra [Portugal]: ACM.
JÖRG, T. & DESSLOCH, S. 2009. Formalizing ETL Jobs for Incremental Loading of Data Warehouses.
JÖRG, T. & DESSLOCH, S. 2010. Near Real-Time Data Warehousing Using State-of-the-Art ETL Tools. Enabling Real-Time Business Intelligence, Lecture Notes in Business Information Processing. Springer-Verlag Heidelberg.
KIMBALL, R. & CASERTA, J. 2004. The Data Warehouse ETL Toolkit, Indianapolis, Indiana, Wiley Publishing, Inc.
KIMBALL, R., REEVES, L., ROSS, M. & THORNTHWAITE, W. 1998. The Data Warehouse Lifecycle Toolkit: Expert Methods for Designing, Developing, and Deploying Data Warehouses, Indianapolis, Indiana, Wiley Publishing, Inc.
KIMBALL, R. & ROSS, M. 2002. The Data Warehouse Toolkit: The Complete Guide to Dimensional Modeling, New York, John Wiley and Sons, Inc.
KIMBALL, R., ROSS, M., THORTHWAITE, W., BECKER, B. & MUNDY, J. 2008. The Data Warehouse Lifecycle Toolkit, John Wiley & Sons.
LABIO, W. J. & GARCÍA-MOLINA, H. 1995. Comparing very large database snapshots. Stanford University.
LABIO, W. J. & GARCÍA-MOLINA, H. 1996. Efficient Snapshot Differential Algorithms for Data Warehousing. Proceedings of VLDB ’96.
MASÓ, A. & CASTELLÓN, Y. 2013. Mercado de datos en apoyo a la toma de decisiones sobre el personal docente e investigativo en el departamento de Recursos Humanos de la UCLV.
Universidad Central “Marta Abreu” de Las Villas.
MUNDY, J. 2008. Design Tip #99 Staging Areas and ETL Tools. Available: http://www.kimballgroup.com/2008/03/04/design-tip-99-staging-areas-and-etl-tools/ .
RAM, P. & DO, L. 2000. Extracting Delta for Incremental Data Warehouse Maintenance. Proceedings. 16th International Conference on Data Engineering (ICDE). IEEE.
ROSS, M. 2013. Design Tip #152 Slowly Changing Dimension Types 0, 4, 5, 6 and 7. Available: http://www.kimballgroup.com/2013/02/05/design-tip-152-slowlychanging-dimension-types-0-4-5-6-7/ .
TELLEZ, Y., MEDINA, D. & TORRES, R. E. 2012. Propuesta para la Implementación de las Dimensiones Lentamente Cambiantes con Pentaho Data Integration.
VASSILIADIS, P. 2009. A survey of Extract–transform–Load technology. International Journal of Data Warehousing & Mining, 5, 1-27.
VILLARREAL, R. X. 2013. Estudio de metodologías de Data Warehouse para la implementación de repositorios de información para la toma de decisiones gerenciales., Universidad Técnica del Norte.
YUAN, G., LI, B. & XIAO, T. 2011. Improvement of Snapshot Differential Algorithm Based on Hadoop Platform. Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC). IEEE.
Recibido: 05/01/2015
Aceptado: 20/02/2015