ARTÍCULO ORIGINAL

 

Algoritmo paralelo para la interpolación espacial de Krigeado Ordinario

 

Parallel algorithm for spatial interpolation of Ordinary Kriging

 

 

Milenis Fernández Díaz^1*,José Gabriel Espinosa Ramirez², César R. García-Jacas³

¹Centro de Geoinformática y Señales Digitales, Universidad de las Ciencias Informáticas. Carretera a San Antonio de los Baños km ½ La Lisa, La Habana, CP. 19370. [e-mail]
²Centro de Ideoinformática, Universidad de las Ciencias Informáticas. Carretera a San Antonio de los Baños km ½ La Lisa, La Habana, CP. 19370. [e-mail]
³Escuela de Sistema y Computación, Pontificia Universidad Católica del Ecuador Sede Esmeraldas (PUCESE), Esmeraldas, Ecuador [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

Los métodos de interpolación espacial proporcionan herramientas para la estimación de valores en localizaciones no muestreadas utilizando las observaciones cercanas. La interpolación de Krigeado Ordinario es uno de los métodos geoestadísticos más frecuentemente usados para la realización de análisis espaciales. Su objetivo consiste en encontrar el Mejor Estimador Lineal Insesgado a partir de los datos disponibles, los cuales generalmente son insuficientes debido al costo de su obtención. Se caracteriza por costosas operaciones de álgebra lineal que repercuten en altos tiempos de ejecución, así como una complejidad temporal de O (MN3). La reducción del tiempo de ejecución de aplicaciones de interpolación espacial puede ser un objetivo de alta prioridad, por ejemplo, en sistemas que soportan la toma de decisiones rápidas. Diversas estrategias han sido aplicadas para reducir los altos tiempos de ejecución de los métodos de interpolación de Krigeado. Las técnicas de programación paralela y distribuida han demostrado ser una alternativa viable para la solución rápida de este tipo de problemas computacionales. Con el objetivo de disminuir los tiempos asociados a la interpolación espacial de Krigeado Ordinario, se propuso un algoritmo paralelo basado en el uso de técnicas de programación en memoria compartida proporcionadas por OpenMP 4.8.2. Este algoritmo fue implementado usando C++11 como lenguaje de programación y Atlas CLapack como biblioteca de álgebra lineal optimizada para los cálculos matriciales. El algoritmo propuesto permite una mayor rapidez en la interpolación espacial de Krigeado Ordinario, logrando un mejor aprovechamiento de los recursos de cómputo instalados.

Palabras clave: computación paralela, interpolación espacial, interpolador geoestadístico, Krigeado Ordinario

---

ABSTRACT

The spatial interpolation methods provide tools for estimating values at unsampled locations using nearby observations. Ordinary Kriging interpolation is one of the most frequently used geostatistical methods for performing spatial analysis. Your goal is to find the Best Linear Unbiased Estimator based on the available data, which are generally insufficient because of the cost of obtaining it. It is characterized by linear algebra expensive operations affecting high execution times and a time complexity of O (MN3). Reducing runtime applications spatial interpolation can be a high priority target, for example, in systems that support rapid decision-making. Various strategies have been applied to reduce high runtimes of Kriging interpolation methods. The techniques of parallel and distributed programming have proven to be a viable alternative for the rapid solution of this type of computational problems. In order to reduce the time associated with spatial interpolation of Ordinary Kriging, was proposed a parallel algorithm based on the use of shared memory programming techniques provided by OpenMP 4.8.2. This algorithm was implemented using C++11 as a programming language and Atlas CLapack as linear algebra library optimized for matrix calculations. The proposed algorithm allows a faster spatial interpolation of Ordinary Kriging, achieving a better utilization of computing resources installed.

Key words: geostatistical interpolator, Ordinary Kriging, parallel computing, spatial interpolation

---

 

 

INTRODUCCIÓN

Los datos espaciales continuos desempeñan un rol significativo en la planeación y la gestión de riesgos ambientales. Los datos espaciales sobre una región de interés son útiles para la toma de decisiones efectivas y seguras, así como la realización de interpretaciones justificadas por parte de los investigadores (Li, y otros, 2008). La reducción del tiempo de ejecución de aplicaciones de interpolación espacial puede ser un objetivo de alta prioridad en sistemas que soportan la toma de decisiones rápidas (Pesquer, y otros, 2011). Usualmente estos datos no cubren completamente el dominio de interés debido a que su adquisición resulta difícil o costosa. En estos casos, los métodos de interpolación espacial proporcionan las herramientas para la estimación de valores en localizaciones no muestreadas utilizando las observaciones cercanas (Li, y otros, 2008).

Las técnicas de interpolación espacial han sido aplicadas a muchas disciplinas tales como la minería (Wang, y otros, 1999), hidrología (Goovaerts, 2000), ciencias ambientales (Jeffrey, y otros, 2001), detección de sismos (Richard, y otros, 1994), ciencias atmosféricas (Vasan Srinivasan, y otros, 2010), entre otras. Se pueden clasificar en 3 categorías: interpoladores no geoestadísticos, interpoladores geoestadísticos y métodos combinados (Li, y otros, 2008). Los métodos geoestadísticos ayudan a los investigadores en la construcción de modelos confiables considerando la variabilidad y correlación espacial del fenómeno en estudio (Allombert, y otros, 2014), así como la estimación de variables ambientales en localizaciones no muestreadas (Gutiérrez de Ravé, y otros, 2014). La interpolación de Krigeado es uno de los métodos geoestadísticos más frecuentemente usados para la realización de análisis espaciales (Kleijnen, 2009).

Las técnicas de Krigeado originalmente fueron desarrolladas por el ingeniero en minas Danie Krige al explotar la correlación espacial para hacer predicciones en la evaluación de reservas de las minas de oro en Sudáfrica (Díaz Viera, 2002). Posteriormente estas técnicas fueron formalizadas por el matemático francés George Matheron (1963) junto a su grupo de la Escuela de Minas de París. El Krigeado constituye un método de interpolación espacial muy utilizado en la construcción de superficies tridimensionales a partir de nubes irregulares de puntos, en la estimación de variables aleatorias en puntos no muestreados, así como en otras aplicaciones de la geoestadística. Especialmente en el área de las Geociencias, es ampliamente utilizado en la estimación de recursos y reservas minerales útiles, considerando el nivel de precisión y confiabilidad que caracteriza sus resultados en estimaciones locales.

El Krigeado tiene como objetivo encontrar el Mejor Estimador Lineal Insesgado a partir de los datos disponibles (Chica Olmo, 1997), los cuales generalmente son insuficientes debido al costo de su obtención. Se basa en la intuición de que las variables espaciales de una determinada población se encuentran correlacionadas en el espacio; es decir, mientras más cercanos estén dos puntos sobre la superficie terrestre menor será la variación de los atributos medidos (Deraisme, y otros, 1996). La formulación matemática del Krigeado aplica “una colección de técnicas generalizadas de regresión lineal para minimizar una varianza de estimación definida de un modelo a priori de covarianza” (Olea, 1991). Se apoya en variogramas como funciones estadísticas que expresan las características de variabilidad y correlación espacial del fenómeno que se estudia a partir de puntos muestreados.

El Krigeado tiene muchas variantes según los grados de estacionariedad de la función aleatoria que representa el fenómeno regionalizado (Krigeado Simple, Krigeado Ordinario, Krigeado Universal, Krigeado de Indicadores, Krigeado Gaussiano) pero la más utilizada es el Krigeado Ordinario. El Krigeado Ordinario asume que la función aleatoria es estacionaria de segundo orden con media desconocida; lo cual indica la homogeneidad de las muestras en el área en la que se distribuye la variable, y además manifiesta que la correlación entre dos variables aleatorias depende únicamente de la distancia espacial que les separa y es independiente de su ubicación (María Montero, y otros, 2008).

El Krigeado Ordinario consiste en la combinación lineal ponderada de los valores muestreados. La estimación de zk se calcula mediante la Ecuación 1:

donde z_k es el valor estimado, z_i son los valores de las muestras, i son los pesos de Krigeado y n es el número de observaciones disponibles.

El Krigeado atribuye un peso a la ley de cada muestra z (x_i), donde los pesos altos corresponden a las muestras cercanas y los pesos débiles a las alejadas. La ponderación depende del modelo ajustado a los puntos medidos, la distancia a la ubicación de la predicción, y las relaciones espaciales entre los valores medidos alrededor de la ubicación de la predicción (ESRI, 2012). Estos pesos se calculan de manera que la varianza del error cometido sea mínima y considerando las características geométricas del problema (Alfaro Sironvalle, 2007). Para garantizar la condición de insesgamiento los pesos deben satisfacer la Ecuación 2, conocida como condición de universalidad:

Este tipo de problema de minimización con restricciones se resuelve utilizando una técnica denominada multiplicadores de Lagrange. Este método involucra la incógnita auxiliar llamada parámetro de Lagrange μ y consiste en igualar a cero las derivadas parciales de la nueva función. Al realizar las N+1 derivaciones se obtiene el sistema de ecuaciones lineales. Los valores de los pesos asociados a cada uno de los puntos se calculan mediante la resolución de este sistema de ecuaciones lineales, compuesto por N+1 ecuaciones con N+1 incógnitas (Alfaro Sironvalle, 2007).

El Krigeado involucra operaciones de diferente índole, dígase: operaciones matriciales (inversión, multiplicación, sistemas de ecuaciones lineales), geométricas (distancia), estadísticas y de procesamiento de datos (Gutiérrez de Ravé, y otros, 2014). Se caracteriza por costosas operaciones de álgebra lineal que repercuten en altos tiempos de ejecución. El análisis computacional del algoritmo realizado por (Pesquer, y otros, 2011) mostró que la resolución del sistema de ecuaciones lineales consume la mayor parte del tiempo de ejecución, aproximadamente de un 96.0% a un 99.8%. En este sentido, se conoce que la complejidad temporal de la resolución de un sistema de ecuaciones lineales usando la eliminación gaussiana regular es de Ο(N³) (Allombert, y otros, 2014).

La complejidad de los cálculos matemáticos utilizados en la interpolación de Krigeado, fundamentalmente la resolución de grandes sistemas de ecuaciones, tiene un alto costo computacional confirmado por varios autores: (Pesquer, y otros, 2011), (Vasan Srinivasan, y otros, 2010), (Kerry, y otros, 1998), (O´Sullivan, y otros, 2002), (Lloyd, 2006). Se plantea que el algoritmo por cada punto de interés tiene una complejidad cúbica, lo que conduce a una complejidad de Ο(MN³), siendo N el número de observaciones disponibles y M el número de puntos a interpolar (Vasan Srinivasan, y otros, 2010). Cuando M≈N la complejidad computacional puede considerarse Ο(N⁴) lo cual no es favorable cuando se trabaja con grandes volúmenes de datos.

Experimentos realizados con diferentes propósitos evidencian la necesidad de rapidez en las operaciones de interpolación espacial, en general. Por ejemplo, en una estación de trabajo con procesador Intel Core2 Quad (4 núcleos) con una frecuencia de 3 GHz y 4 GB de memoria RAM, para un juego de datos compuesto por 8 millones de puntos, el tiempo de ejecución fue de aproximadamente dos días (Vasan Srinivasan, y otros, 2010). Otro experimento realizado sobre 486,400 puntos en un procesador Pentium IV de 2.6 GHz con 768 MB de RAM, tardó 11 h 26 m 12 s (Pesquer, y otros, 2011).

Con el objetivo de disminuir los tiempos asociados a la interpolación espacial de Krigeado Ordinario, se propone un algoritmo basado en el uso de técnicas de programación paralela; que permita resolver los problemas que satisfacen los supuestos matemáticos apropiados en tiempos razonables, fundamentalmente en el campo de las Geociencias.

 

MATERIALES Y MÉTODOS

Arquitectura paralela

Diversas estrategias han sido aplicadas para reducir los altos tiempos de ejecución de los métodos de interpolación de Krigeado. En la literatura se identifican soluciones simples basadas en acelerar la búsqueda de las observaciones cercanas (Hessami, y otros, 2001), así como formas optimizadas de resolución de los sistemas de ecuaciones lineales (Allombert, y otros, 2014); y más recientemente, el uso de redes neuronales y la aplicación de técnicas de programación paralela, ya sea en entornos de memoria compartida o en arquitecturas distribuidas. Las técnicas de programación paralela y distribuida han demostrado ser una alternativa viable para la solución rápida de este tipo de problemas computacionales.

Muchas de las soluciones propuestas para la aceleración de los cálculos en la interpolación de Krigeado aprovechan la escalabilidad que ofrecen las técnicas de computación paralela en entornos distribuidos. Dígase: supercomputadoras o clústeres (Kerry, y otros, 1998), distribución de cálculos usando MPI (Message Passing Interface) en entornos de alto rendimiento (HPC, High Performance Computing) (Pesquer, 2011; Lu, 2004) y cálculos de geoprocesamiento sobre la nube aplicando técnicas de Map/Reduce (Osorio Murillo, 2011). Desafortunadamente, en el país son pocas las instituciones que disponen de entornos de alto rendimiento; y en muchas empresas el número de estaciones de trabajo es limitado. Considerando estos elementos se descarta este tipo de soluciones en la presente investigación.

Publicaciones recientes señalan la utilización de GPU (Graphic Processing Unit) como una alternativa eficiente para la interpolación de Krigeado, describiéndose muy buenos resultados de aceleración en (Gutiérrez de Ravé, y otros, 2014), (Cheng, 2013). Se identifica el uso de la computación general en unidades de procesamiento gráfico como una tendencia para abordar problemas de interpolación, aprovechando la optimización de operaciones matriciales y las posibilidades de procesamiento paralelo masivo de estos dispositivos. Sin embargo, la cantidad limitada de memoria disponible en estos aceleradores constituye un cuello de botella (Allombert, y otros, 2014). Por otra parte, la utilización de este tipo de dispositivo de hardware obliga a programar para fabricantes específicos, además de que estos dispositivos son altamente costosos.

Las tendencias actuales en el desarrollo de hardware están encaminadas a la incorporación de más núcleos en los procesadores, en lugar del incremento de la velocidad del reloj de los procesadores. Hoy día es común encontrar sistemas multinúcleos en las empresas e instituciones nacionales. Por tal motivo, el algoritmo propuesto estará dirigido al aprovechamiento eficiente de las capacidades de procesamiento de los sistemas multinúcleos, adaptándose a las características del hardware subyacente. Esta adaptación permite obtener mejores rendimientos mientras mayores sean las capacidades de procesamiento paralelo de los equipos (Campbell, y otros, 2011).

Herramientas y tecnologías

El algoritmo de Krigeado Ordinario fue implementado usando C++11 como lenguaje de programación. Para los cálculos matriciales se utilizó la biblioteca de álgebra lineal Atlas CLapack, caracterizada por ser rápida. Esta biblioteca permitió simplificar el cálculo de operaciones matriciales como la solución de sistemas de ecuaciones lineales, así como la multiplicación de matrices. Se aplicaron técnicas de programación paralela en memoria compartida a través de la biblioteca OpenMP 4.8.2.

La biblioteca OpenMP se compone de un conjunto de directivas de compilador que permiten especificar qué regiones de código van a ser paralelizadas, así como una biblioteca de rutinas en tiempo de ejecución y un conjunto de variables de entorno. Se basa en el modelo fork-join para obtener el paralelismo a través de múltiples hilos. Este modelo plantea la división del hilo maestro en hilos esclavos que se ejecutan concurrentemente, distribuyéndose las tareas sobre estos hilos. Estos hilos acceden a la misma memoria, aunque es posible gestionar estos accesos generando espacios de memoria privada (Chapman, y otros, 2008).

Modelación del algoritmo

En el proceso de Krigeado se recomienda establecer una vecindad de búsqueda para evitar el trabajo con grandes sistemas de ecuaciones lineales, que requieren altos tiempos de resolución. Los sistemas mineros reconocidos internacionalmente permiten la definición de una vecindad de búsqueda que limite el número de ensayos geoquímicos a utilizar en las estimaciones de Krigeado. El dominio de vecindad puede obtenerse con reducciones proporcionales en cada uno de los alcances o a través de cuadrantes u octantes (Cuador Gil, 2002).

El proceso de Krigeado involucra como primer paso el modelado de la autocorrelación espacial de los datos, lo que se conoce como variografía o análisis estructural. La construcción del variograma experimental y su posterior ajuste al variograma teórico que mejor se aproxime a la curva obtenida, se recomienda realizar de forma visual o interactiva (Cuador Gil, 2002) aprovechando la experticia de los especialistas funcionales.

Esta importante tarea queda en manos de los especialistas funcionales, por lo que constituye una entrada a proporcionar al algoritmo.

A partir de la información proporcionada por el variograma y considerando la vecindad de estimación definida, el próximo paso consiste en la realización de las predicciones. Este último paso requiere previamente el cálculo de los pesos asociados al punto a interpolar, que luego son utilizados para el cálculo del valor del punto en cuestión y del error de estimación. Este conjunto de pasos se repite para cada uno de los puntos a predecir o estimar.

El algoritmo de Krigeado Ordinario requiere como entradas:

• Ensayos o puntos medidos (representados por sus coordenadas espaciales y los valores del atributo medido).

• Puntos a estimar o modelo de bloques. El modelo de bloques consiste en una matriz tridimensional de celdas (comúnmente llamadas bloques), las cuales conforman el volumen de interés.

• Vecindad de estimación: “Subconjunto del dominio que contiene el punto s0 en el que se quiere estimar la función aleatoria y las localizaciones muestrales correspondientes a las observaciones que van a ser utilizadas en la estimación” (María Montero, y otros, 2008) (representada por un elipsoide o esfera).

• Variograma: Función estadística que expresa las características de variabilidad y correlación espacial del fenómeno que se estudia a partir de puntos muestreados (representado por el tipo de variograma, el valor de pepita, el rango y la meseta).

El algoritmo genera como salidas: los puntos o bloques estimados (zk) y la varianza del error de estimación asociada a los puntos o bloques estimados.

Diseño del algoritmo

El diseño del algoritmo se basó en las siguientes etapas: partición (descomposición de la computación de tareas), comunicación (coordinación en la ejecución de tareas), aglomeración (combinación de los resultados de las tareas) y mapeo (asignación de tareas a los procesadores); descritas en (Foster, 1995), (Naiouf, 2004). Se centró fundamentalmente en la partición y asignación. En el diseño del algoritmo no se presentaron secciones críticas, por lo que no se hacen copias de la lista de puntos a interpolar; todos los procesos pueden leer y escribir en esta lista sin que se generen conflictos de memoria.

En la partición el cómputo y los datos sobre los cuales se opera se descomponen en tareas, ignorando aspectos como el número de procesadores. Existen dos formas de descomponer las tareas: descomposición del dominio (paralelismo de datos) o descomposición funcional (paralelismo de control o de tareas). Aprovechando la independencia de los datos de entrada se aplica la descomposición del dominio para la división de los datos entre los procesadores. Esta técnica de descomposición consiste en determinar la partición apropiada de los datos, y luego trabajar en los cómputos asociados.

En la etapa de asignación, cada tarea es asignada a un procesador tratando de maximizar la utilización de los procesadores y de reducir el costo de comunicación. La asignación puede ser estática o dinámica; ambas formas se utilizan en el presente trabajo. La asignación estática consiste en distribuir las tareas entre los procesadores al iniciar la ejecución del algoritmo, mientras que en la asignación dinámica la distribución de las tareas se realiza en tiempo de ejecución a través de algoritmos de balanceo de carga. En el algoritmo propuesto el balanceo de carga se logra mediante una variante del ordenamiento merge sort que en lugar de explotar la recursividad se basa en particiones apropiadas de los datos.

Evaluación experimental

Se realizó la evaluación experimental del algoritmo variando el tamaño de entrada (n) y el número de procesadores (p). En función de estos parámetros, los algoritmos fueron evaluados atendiendo al tiempo de ejecución, la ganancia de velocidad (Speed Up) y la eficiencia (E). Se entiende por tiempo de ejecución como el tiempo que transcurre desde el comienzo de la ejecución del programa en el sistema paralelo, hasta que el último procesador culmine su ejecución.

A la ganancia de velocidad también se le conoce como aceleración, y consiste en la relación entre el tiempo de ejecución sobre un procesador secuencial y el tiempo de ejecución sobre múltiples procesadores (Grama, y otros, 2003) Por eficiencia se entiende el porcentaje de tiempo empleado en proceso efectivo (Müller, 2011); este indicador mide el grado de utilización de un sistema multiprocesador.

Los experimentos se ejecutaron en una estación de trabajo Acer Aspire 5755 con procesador Intel (R) Core (TM) i5-2430, con una frecuencia de 2.40 GHz, 4 GB de memoria instalada y sistema operativo Ubuntu 14.04 (32 bits). Se utilizaron 3 juegos de datos generados aleatoriamente variando el número de ensayos; así como un modelo de variograma lineal de 1 como valor de pepita, y 10 como valor de meseta (Ecuación 3).

donde: C₀ es el valor de pepita, C es el valor de meseta y h es la distancia entre los puntos.

Se utilizó una vecindad esférica de 5 metros de radio. Los juegos de datos estaban compuestos por 1000 bloques y 1000 ensayos, 1000 bloques y 2000 ensayos, 1000 bloques y 3000 ensayos, respectivamente. El proceso de Krigeado se realizó de forma puntual considerando los centroides de los bloques como la nube de puntos a estimar. Se realizaron 10 corridas en cada experimento, descartándose los datos atípicos a través del método de los cuartiles.

 

RESULTADOS Y DISCUSIÓN

El algoritmo que se propone para la interpolación de Krigeado Ordinario consta de 3 etapas de procesamiento paralelo a través del modelo fork-join. La primera etapa se ocupa de la indexación espacial de los ensayos en el modelo de bloques y la búsqueda de vecinos a utilizar en cada una de las interpolaciones. Para la ejecución de estos subprocesos los puntos a interpolar (llamados bloques) son distribuidos en trozos de aproximadamente igual tamaño entre los procesadores mediante asignaciones estáticas (schedule static); todas las iteraciones son repartidas de forma continua antes de ser ejecutadas. Una vez que se determinan las observaciones cercanas a utilizar en cada estimación, el próximo paso consiste en ordenar los puntos a interpolar según el número de observaciones cercanas, con el fin de lograr una partición de los datos que equilibre la carga de los procesadores.

El subproceso de ordenamiento de los datos se realiza en la segunda etapa, para lo cual la lista de puntos a interpolar es particionada en tantas partes iguales como número de procesadores; luego estas partes son ordenadas simultáneamente. Una vez concluye el proceso de ordenamiento, se mezclan los resultados arrojados por cada procesador en tantas iteraciones como sean necesarias. Finalmente, en la última etapa los puntos a interpolar se distribuyen nuevamente entre los procesadores, pero esta vez de forma dinámica (schedule dynamic), es decir las iteraciones son asignadas de forma continua a solicitud de los procesadores, hasta que se acaben. En esta etapa se calculan los pesos y los valores asociados a los puntos a interpolación.

Los resultados alcanzados mediante el algoritmo paralelo propuesto serán abordados a continuación (Tabla 1):

Los datos arrojados por la evaluación experimental del algoritmo evidencian una disminución de los tiempos requeridos en la interpolación de Krigeado ordinario (Figura 1).

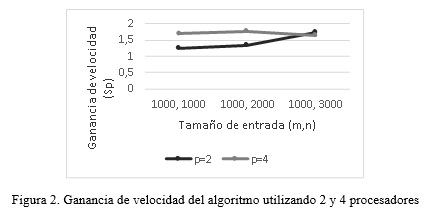
La mayor ganancia de velocidad (1.77) se obtuvo para un tamaño de entrada de m=1000 (bloques) y n=2000 (ensayos), donde se logró disminuir el tiempo de ejecución de 6789 ms a 3844 ms al utilizar 4 procesadores (Figura 2). La ganancia de velocidad incrementa al aumentar el tamaño de entrada atendiendo a su valor óptimo cuando se utilizan 2 procesadores. Por otro lado, los valores de eficiencia indican un aprovechamiento del 62.5% al 86.54% de las capacidades de procesamiento al utilizar 2 procesadores, y un aprovechamiento cercano a la mitad al utilizar 4 procesadores. Se evidencia un notable incremento de la eficiencia al aumentar los tamaños de entrada con el uso de 2 procesadores.

Se observa una disminución de la ganancia de velocidad y la eficiencia al utilizar 4 procesadores para un tamaño de entrada de 1000 bloques y 3000 ensayos, lo cual está influenciado por el procesamiento de ordenamiento de los datos en busca de equilibrar la carga entre los procesadores. Si bien el ordenamiento por mezcla fue implementado de forma paralela, a medida que se incrementan las iteraciones se van desechando procesadores al mezclar los resultados parciales. Esto se va acentuando en la medida que aumentan los tamaños de entrada y el número de procesadores.

 

CONCLUSIONES

• La adaptación de los algoritmos y aplicaciones a las características del hardware subyacente permitirá la obtención de mejores rendimientos mientras mayores sean las capacidades de procesamiento paralelo de los equipos.
• La computación general en unidades de procesamiento gráfico marca la tendencia actual para lograr la aceleración de la interpolación de Krigeado, aprovechando la optimización de operaciones matriciales, y las posibilidades de procesamiento paralelo masivo de estos dispositivos.
• El carácter independiente de los datos utilizados en el proceso de Krigeado Ordinario favorece la utilización del paralelismo a nivel de datos como una alternativa eficiente para disminuir los tiempos de respuesta asociados.
• Las técnicas de programación paralela en memoria compartida facilitan la explotación del paralelismo de datos a través del uso de bucles iterativos para la distribución de tareas a los procesadores, propiciando un mejor aprovechamiento de las capacidades de cómputo.
• La subdivisión de los bloques en diferentes procesadores es muy útil cuando se trabaja con grandes cantidades de datos, pero si no se logra una distribución equitativa el aprovechamiento de los núcleos de procesamiento no será óptimo.

 

AGRADECIMIENTOS

Se agradece la colaboración del Dr. José Quintín Cuador Gil de la Universidad de Pinar del Río y del especialista José Arias de la Oficina Nacional de Recursos Minerales (ONRM).

 

REFERENCIAS BIBLIOGRÁFICAS

ALFARO, M. A. Estimación de Recursos Mineros, 2007. Disponible en: www.cg.ensmp.fr/bibliotheque/public/ALFARO_Cours_00606.pdf

ALLOMBERT, V.; MICHEA, D.; et al. An out-of-core GPU approach for accelerating geostatistical interpolation. En: 14th International Conference on Computational Science and Its Applications (ICCSA 2014). Procedia Computer Science, University of Minho, 2014, 29, p. 888–896.

CAMPBELL, C.; MILLER, A. Parallel programming with Microsoft Visual C++. Design patterns for decomposition and coordination on multicore architectures, Microsoft, 2011, 208p.

CHAPMAN, B.; JOST, G.; et al. Using OpenMP Portable Shared Memory Parallel Programming, London, The MIT Press, 2008, 384p.

CHENG, T. Accelerating universal Kriging interpolation algorithm using CUDA enabled GPU. Computers & Geosciences, 2013, 54, p. 178-183.

CHICA, M. Análisis Geoestadístico en el Estudio de la Explotación de Recursos Minerales. Tesis doctoral, Universidad de Granada, España, 1987.

CUADOR, J. Q. Estudios de estimación y simulación geoestadística para la caracterización de parámetros geólogo industriales en el yacimiento laterítico Punta Gorda. Tesis doctoral, Universidad de Pinar del Río, Pinar del Río, 2002.

DERAISME, J.; DE FOUQUET, Ch. The geostatistical approach for reserves, Mining Magazine, 1996.

DÍAZ, M. A. Geoestadística Aplicada, Instituto de Geofísica, UNAM, 2002.

ESRI. ArcGIS Help 10.1 [online], 2012 [Consultado en junio de 2015]. Disponible en: http://resources.arcgis.com/en/help/main/10.1/index.html#//009z00000076000000.

FOSTER, I. Designing and Building Parallel Programs, Chicago, Addison Wesley, 1995, 430p.

GOOVAERTS, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. Journal of Hidrology, 2000, 228 (1-2), p. 113-129.

GRAMA, A.; GUPTA, A. Introduction to Parallel Computing, Addison Wesley, 2003, 656p.

GUTIÉRREZ, E.; JIMÉNEZ, F. J.; et al. Using general-purpose computing on graphics processing units (GPGPU) to accelerate the ordinary kriging algorithm, Computers & Geosciencies, 2014, (64), p. 1-6.

HESSAMI, M.; ANCTIL, F.; et al. Delaunay implementation to improve kriging computing efficiency. Computers & Geosciences, 2001, (27), p. 237-240.

JEFFREY, S. J.; CARTER, J. O.; et al. Using spatial interpolation to construct a comprehensive archive of Australian climate data, Environmental Modelling & Software, 2001, 16 (4), p. 309-330.

KERRY, K. E.; Hawick, K. A. Kriging interpolation on high-performace computers, Department of Computer Science, Universidad de Adelaide, TR: DHPC-035, Australia,1998.

KLEIJNEN, J. P. Kriging metamodeling in simulation, European Journal of Operational Research, 2009, 192(3), p. 707-716.

LI, J.; HEAP, A. D. A Review of Spatial Interpolation Methods for Environmental Scientists. Canberra, Geoscience Australia, 2008, 137p.

LLOYD, C. D. Local models for spatials analysis, Belfast First Edition CRC Press, 2006, 352p.

LU, K.; GODDARD, S. GRASS-based High Performance Spatial Interpolation Component for Spatial Decision Support Systems, Proceedings of the FOSS/GRASS Users Conference, Thailand, Bangkok, 2004.

MARÍA, J.; LARRAZ, L. B. Introducción a la geoestadística lineal, NetBiblo S.L., La Coruña, 2008.

MÜLLER, L. Evaluación del rendimiento de algoritmos paralelos y/o concurrentes, Universidad Americana, 2011.

NAIOUF, R. M. Procesamiento paralelo. Balance de carga dinámico en algortimos de sorting, Tesis doctoral, Universidad Nacional de La Plata, Argentina, 2004.

OLEA, R. Geostatistical glossary and multilingual dictionary, Oxford University, New York, 1991.

OSORIO, C. A. Parallelization of Web Processing Services on Cloud Computing: A case study of Geostatistical Methods. Tesis del maestría en Geospatial Technologies, Castellon de la Plana, 2011.

O´SULLIVAN, D.; UNWIN, D. Geographic Information Analysis, New Jersey, John Wiley & Sons Hoboken, 2002, 432p.

PESQUER, L.; CORTÉS, A.; et al. Parallel ordinary kriging interpolation incorporating automatic variogram fitting. Computers & Geosciences, 2011, (37), p. 464–473.

RICHARD, E. R.; JENNIFER, L. D.; et al. Kriging in the shadows: Geostatistical interpolation for remote sensing, Remote Sensing of Environment,  1994, 49 (1), p. 32-40.

VASAN, B.; DURAISWAMI, R.; et al. Efficient kriging for real-time spatio-temporal interpolation. En: 20th Conference on Probability and Statistics in the Atmospheric Sciences. American Meteorological Society, 2010, p. 228-235.

WANG, L.; WONG, P. M.; et al. Combining neural networks with kriging for stochastic reservoir modeling. In Situ, 1999, 23 (2), p. 151-169.

 

 

Recibido: 25/03/2016
Aceptado: 30/06/2016