ARTÍCULO ORIGINAL

 

Evaluación del algoritmo KNN-SP para problemas de predicción con salidas compuestas

 

Evaluation of KNN-SP algorithm for multi-target prediction problems

 

 

Héctor González^1*,Gabriela Santos¹, Frank Campos¹, Carlos Morell Pérez²

¹Universidad de las Ciencias Informáticas (UCI), La Habana, Cuba. {gsantos, frcampos}@uci.cu
²Universidad Central de las Villas “Marta Abreu” (UCLV), Villa Clara, Cuba. [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

El presente trabajo pretende desarrollar una evaluación estadística del algoritmo KNN para problemas de predicción con salidas compuestas. Se utiliza el procedimiento de validación cruzada para ajustar el parámetro y la variante de peso inverso generando 4 variantes del KNN para predicción con salidas compuestas. El estudio de los métodos estadísticos para la comparación de múltiples clasificadores permitió identificar la prueba no paramétrica de Friedman como una de las más empleadas en la experimentación de algoritmos de aprendizaje automático. Se utilizaron 12 bases de datos estándares y la métrica aRRMSE para la evaluación experimental de los resultados. La aplicación de las pruebas de Friedman y el post-hoc de Nemenyi mostraron que el procedimiento de validación cruzada aplicados en las variantes IBKMTRCV y IBKMTRCVW es significativamente mejor que las variantes que no utilizan dicho procedimiento. Al utilizar los valores de los ranking promedios de la prueba de Friedman ubican a la variante IBKMTRCVW como la que mejores resultados arroja.

Palabras clave: aprendizaje automático, comparación de múltiples clasificadores, KNN, Predicción con salidas compuestas

---

ABSTRACT

This paper aims to develop a statistical evaluation of KNN algorithm for multi-target prediction problems. The cross-validation procedure is used to set the parameter and inverse distance as weigth to generate 4 variants of KNN for muti-target prediction. The study of statistical methods for comparison of multiple classifiers identified the non-parametric Friedman test as one of the most used in the testing of machine learning algorithms. In the experimental results, it employ 12 standards dataset and the metric aRRMSE. With application of the Nemenyi  post-hoc and Friedman tests showed that cross-validation procedure applied in IBKMTRCV and IBKMTRCVW is significantly better than the variants that do not use this procedure. The values of the average ranking of the Friedman test, show that IBKMTRCVW algorithm returns the best results.

Key words: machine learning, comparisons of multiple classifiers, KNN, Multi-target prediction

---

 

 

INTRODUCCIÓN

La evaluación estadística de resultados experimentales es una parte esencial para la validación de los métodos de aprendizaje automático. En un trabajo de aprendizaje automático generalmente se propone un nuevo algoritmo, un modelo o parte de estos y la hipótesis implícita en este problema, que es demostrar que esta nueva propuesta mejora significativamente lo reportado en el estado del arte. Para ello se define un conjunto de datos de prueba representativos del dominio de aplicación para el cual fue diseñado el algoritmo, el cual se utilizará en la evaluación de la propuesta. Luego se ejecuta el algoritmo propuesto con los algoritmos de la competencia en igualdad de condiciones y sobre los mismos conjuntos de datos. Se evalúan los resultados de cada algoritmo con sus bases de datos usando una métrica apropiada para cuantificar su desempeño. Es importante resaltar que existe un número considerable de métricas para evaluar el desempeño de algoritmos sin embargo en problemas de clasificación lo más común es usar la precisión. Finalmente, se debe verificar estadísticamente la hipótesis de un mejor desempeño de la nueva propuesta con relación a lo que esté reportado.

Existen diversos trabajos de referencia dirigidos a estudiar, en el área de la estadística, los diversos enfoques para contrastar los resultados de investigación en el campo del aprendizaje automático (Demšar, 2006)(García, Fernández, Luengo, & Herrera, 2009). En general, estos trabajos se han encaminado a profundizar y evaluar diversos enfoques de pruebas estadísticas y recomendar para cada diseño experimental las mejores prácticas. Existen esencialmente dos enfoques de pruebas estadísticas ampliamente utilizadas en la experimentación de problemas de aprendizaje automático que son las pruebas paramétricas y las no paramétricas. En el caso de las pruebas paramétricas asumen que los datos primarios se ajustan a una distribución teórica de probabilidades y hacen inferencia sobre los parámetros de la distribución. De este modo al aplicar una prueba paramétrica como es el caso de la prueba ANOVA es necesario verificar independencia, normalidad y homogeneidad de varianza de los datos. A pesar de que no siempre es posible que se cumplan estas condiciones siempre es preferible aplicar pruebas paramétricas por encima de las no paramétricas.

Por otra parte la prueba no paramétrica similar es la Prueba de Friedman (Friedman, 1940) la cual jerarquiza los algoritmos por cada colección de datos separadamente y en caso de empate asigna un rango promedio.

En los últimos años, en la rama del aprendizaje automático, han aparecido problemas de la vida práctica donde se hace necesario modelar la predicción a través de estructuras complejas en su salida. Estos problemas están relacionados con la necesidad de predecir valores de salidas en forma de: grafos, jerarquías, vectores con valores reales o binarios entre otras. Como término general este tipo de tarea es conocida como problemas de predicción estructurada (Nowozin, Gehler, Jancsary, & Lampert, 2014).

Un ejemplo que ilustra la necesidad de estudiar la predicción con salidas estructuradas se describe a continuación. Para un problema de clasificación de objetos presentes en imágenes con predominio de paisajes no es posible clasificar de forma independiente regiones de una imagen con nubes y al mismo tiempo imágenes de árboles sin tomar en cuenta la relación que existe entre estos objetos para este tipo de imágenes (Lam, Rao Doppa, Todorovic, & Dietterich, 2015). Otras áreas de aplicación donde se han modelado problemas de predicción con salidas estructurados son en el procesamiento del lenguaje natural (Goldwasser, Srikumar, & Roth, 2012) y la bioinformática (Savojardo, Fariselli, Martelli, & Casadio, 2013)(Yang, Wang, & Zuo, 2013).

Como caso particular de problemas con salidas estructuradas se encuentran los problemas de predicción con salidas compuestas donde se trata de predecir un vector de salida (la variable objetivo es un vector con valores reales). Por lo tanto, un problema de predicción con salidas compuesta intenta predecir de forma simultánea y con un único modelo todos los atributos del espacio de salida expresados en forma vectorial. Los problemas de predicción con salidas compuestas han sido estudiados desde diferentes enfoques dentro del aprendizaje automático. Una taxonomía que ordena los diversos enfoques de aprendizaje con salidas compuesta es propuesto en (Borchani, Varando, Bielza, & Larrañaga, 2015). En este trabajo se describen dos grandes familias de algoritmos, los basados en adaptación de métodos y los basados en transformación del problema. En el primer caso, se hace extensión de manera natural de los algoritmos clásicos de aprendizaje automático para obtener un único modelo que prediga de manera simultánea cada salida. En el segundo caso se encuentran los algoritmos que realizan alguna transformación de las variables predictoras teniendo en cuenta las variables objetivos para obtener uno o varios modelos de predicción. En ambas familias de algoritmos se toma en cuenta la interdependencia entre las variables de salidas.

Por otra parte, el algoritmo de aprendizaje automático -Vecinos más Cercanos (Cover & Hart, 1967) (KNN por sus siglas en inglés) está considerado uno de los de mejor desempeño en el ámbito del aprendizaje automático. Al mismo tiempo, el KNN construye un modelo sencillo para resolver problemas de predicción el cual está basado en los objetos del conjunto de datos de entrenamiento. En KNN para un nuevo ejemplo, se asigna al atributo de la clase, el valor medio de las clases de los objetos que se encuentran dentro de la frontera de los  vecinos más cercanos. En general la distancia Euclidiana es empleada para medir la proximidad entre el nuevo ejemplo y los que conforman el conjunto de datos de entrenamiento. 

Sin embargo, a pesar del buen desempeño del KNN para problemas de predicción este no ha sido ampliamente utilizado para problemas donde se desee predecir un vector de salida. Solo se encontró reportado en la literatura el trabajo (Pugelj & Džeroski, 2011) que utiliza el KNN con distancia Euclidiana y emplea distancia inversa para manejar los pesos. Sin embargo en este trabajo no queda fuertemente validado el KNN ya que de forma empírica los autores utilizan un valor fijo de K=25. Un análisis más profundo exploraría, para cada base de datos, la mejor configuración del algoritmo KNN usando procedimientos como el de validación cruzada (Selección del mejor K). Por otra parte, no se hace una evaluación de este algoritmo con un conjunto de bases de datos existentes en la literatura para problemas de predicción con salidas compuestas, así como otras que han surgido recientemente. En la definición básica del KNN-SP propuesto en (Pugelj & Džeroski, 2011) se considera una variante simple de modelo de transformación.

Tomando en cuenta los elementos anteriormente planteados nos proponemos en nuestra investigación desarrollar un estudio del algoritmo KNN para problemas de predicción con salidas compuestas utilizando un mecanismo de validación cruzada extendido para este tipo de problemas, así como el estudio de la influencia de la distancia inversa como peso para este tipo de problemas. De igual manera la experimentación de este algoritmo en 12 bases de datos estándares y la selección de las mejores configuraciones para cada base de datos formaran parte de los resultados de esta investigación.

 

MATERIALES Y MÉTODOS

En el presente trabajo usaremos las siguientes definiciones y notaciones para describir nuestro problema de predicción con salidas compuestas.

Sea el conjunto de variables o atributos de entrada y el conjunto de atributos de salidas definidos para observaciones . El objetivo en la tarea de predicción con salidas compuestas es aprender un modelo único de modo que pueda predecir de forma simultánea el conjunto de variables de salidas. En este sentido cualquier objeto se puede predecir sus variables de salidas utilizando las variables predictoras a través del modelo = h( ).

En el caso del algoritmo KNN se predice una variable de salida a partir de la media (Para datos numéricos) de los -vecinos más cercanos sobre el conjunto de atributos de entrada. Su generalización a problemas de predicción con salidas compuestas consiste en determinar el valor medio para cada salida de los K-vecinos más cercanos. Formalmente podemos platear que, para cada objeto a predecir y sus correspondientes conjuntos de los k-vecinos más cercanos el valor que se predice para la variable de salida será:

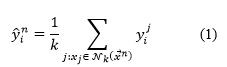
Para determinar la proximidad entre cada objeto del conjunto de entrenamiento y los objetos a predecir se emplea una función de distancia (En general distancia Euclidiana para datos numéricos). Para determinar la distancia Euclidiana entre dos vectores del espacio de entrada se calcula:

En el proceso de predicción se puede utilizar como pesos la distancia inversa d^-1 por cada objeto con respecto a sus vecinos. En este enfoque el valor de los vectores de salidas se obtendría como la media ponderada por la distancia de valores de salidas por cada vecino:

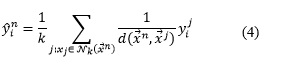
Uno de los problemas esenciales en los algoritmos de aprendizaje automático es el ajuste de sus parámetros de entrada, ya que al aplicar estos con diferentes configuraciones los resultados pueden sufrir cambios considerables. En particular el algoritmo KNN requiere de conocer de antemano el valor de k para determinar los K vecinos más cercanos. Un procedimiento común para evaluar diferentes configuraciones de KNN es el conocido como Hold out cross validationen el cual se emplea el conjunto de datos de entrenamiento para clasificar cada objeto de este según el modelo obtenido. En este procedimiento se ejecuta varias veces el algoritmo KNN para diferentes valores de k y se cuantifica una métrica de error que permite determinar la mejor configuración. En nuestro problema de predicción con salidas compuesta se utiliza la métrica promedio del error relativo cuadrático medio aRRMSE la cual es usado en la experimentación del trabajo (Spyromitros-Xioufis, Tsoumakas, William, & Vlahavas, 2014) referente del estado del arte en este tipo de problemas.

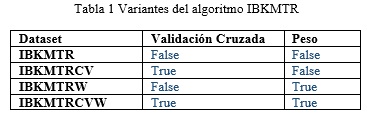
Para la implementación del algoritmo se empleó la herramienta MULAN (Tsoumakas, Spyromitros-Xioufis, Vilcek, & Vlahavas, 2011) la cual incorpora varios algoritmos de predicción con salidas compuestas en el paquete mulan.regressor.transformation. Mulan es una plataforma de software libre para problemas de salidas múltiples (clasificación multi-etiqueta, clasificación de salidas compuestas). La herramienta MULAN contiene la mayor parte de los algoritmos de predicción con salidas compuestas propuestos en la literatura. Solo el PCR y el PCT (Aho, Ženko, Džeroski, & Elomaa, 2012) se encuentran en CLUS los cuales pueden ser ejecutados e implementados en la herramienta MULAN a través del paquete mulan.regressor.clus contenido en ella. Se implementó la Clase IBKMTR.java la cual considera 4 combinaciones del algoritmo relacionados con las variantes de usar o no peso y usar o no validación cruzada.

La tabla 1 muestra las diferentes variantes del algoritmo.

Comparación estadística de múltiples clasificadores

Siguiendo las recomendaciones de (Demšar, 2006), el método estadístico común para esta tarea es ANOVA para análisis paramétrico. Una de las desventajas de ANOVA es que está basada en asunciones, las cuales, en el ámbito experimental de los algoritmos de aprendizaje automático, son posiblemente violadas. Primeramente, ANOVA asume que las muestras son extraídas de distribuciones normalizadas. La segunda y más importante asunción de ANOVA es la esfericidad. La esfericidad es una propiedad que requiere que las variables aleatorias tengan igual varianza y que debido a la naturaleza de los algoritmos de aprendizaje y las colecciones de datos no se puede dar por hecho. Violaciones de estas asunciones tiene un efecto aún mayor en las Pruebas post-hoc, por lo que ANOVA no es frecuente su uso para estudios experimentales de aprendizaje automático.

Un equivalente no paramétrico de ANOVA es la Prueba de Friedman (Friedman, 1940) la cual jerarquiza los algoritmos por cada colección de datos separadamente y en caso de empate asigna un rango promedio. Tomando como el rango del algoritmo j de k posibles algoritmos en la i-ésima colección de datos de  colecciones de datos, la Prueba de Friedman compara los rasgos promedios de los algoritmos La hipótesis nula afirma que todos los algoritmos son equivalentes y por eso sus rangos R_j deberían ser iguales. Bajo esta hipótesis nula, la estadística de la Prueba de Friedman se calcula:

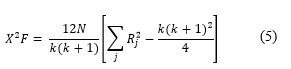
De acuerdo a con k - 1 grados de libertad cuandok y N  son lo suficientemente grandes k>5, N>10. Si la hipótesis nula es rechazada se puede proceder con una Prueba de post-hoc. La Prueba de Nemenyi (Nemenyi, 1962) es similar a la de Tukey para ANOVA y es usado cuando los clasificadores son comparados entre sí. El desempeño de cualesquiera dos mediciones modeladas en el experimento es significativamente diferente si la diferencia entre estas excede al menos la Diferencia Crítica. Los valores críticos son determinados usando el estadístico del rango Studentized dividida por . Esta diferencia crítica se calcula de la siguiente manera:

Teóricamente la Prueba de Friedman no paramétrica tiene menos poder que el ANOVA paramétrico cuando las asunciones de ANOVA se cumplen, en caso contrario no necesariamente. Friedman en su trabajo (Friedman, 1940) realizó 56 experimentos relacionados con diversos problemas independientes y demostró que ambos coincidían generalmente. Cuando uno encontraba un nivel de significación en p< 0.01 el otro en al menos p< 0.5 respectivamente. Solamente en dos casos ANOVA encontró nivel de significación que era insignificante para Friedman, mientras que en caso contrario ocurrió en 4 pruebas.

 

RESULTADOS

En el trabajo (Spyromitros-Xioufis et al., 2014) se proponen varios algoritmos de predicción con salidas compuestas los cuales fueron evaluadas con 12 bases de datos estándares que se han establecido en este ámbito. De estas bases datos 4 fueron propuestos como resultado de este trabajo. En la validación del algoritmo KNN-SP solo se utilizaron 2 de estas bases de datos por lo que su evaluación en el resto de las bases de datos se hace necesario para comparar sus resultados con otros algoritmos en este ámbito.

Estas bases de datos se relacionan en la tabla2. donde la primera columna indica el nombre de la base de datos, la segunda se refiere al número de observaciones de la base de datos. En esta columna además se indica si los datos están particionados en datos de prueba (test) y datos de entrenamiento (train) o si la base de datos contiene todos los datos los cuales deben ser particionados para los experimentos. Para particionar los datos se utiliza un método de validación cruzada el cual se conoce como K-Fold Cross Validation (lo señalamos como CV). La 3ra y 4ta columna indica la cantidad de atributo en el espacio de entrada y salida respectivamente. La última columna brinda una breve explicación del dominio de aplicación en el cual fueron colectados los datos.

Como medida de evaluación se empleó el promedio del error relativo cuadrático medio (aRRMSE) entre lo predicho por el algoritmo y lo medido en cada base de datos para las variables de salidas. El mismo se determina de la siguiente manera:

Para validar los resultados de la presente investigación se ejecutaron 10-Fold Cross Validation para las bases de datos no particionadas. Se ejecutaron las cuatro variantes descritas anteriormente del algoritmo IBMTR en los cuales para las variantes IBKMTR y IBKMTRW se utilizó k=25  similar a (Pugelj & Džeroski, 2011). En los casos de los algoritmos que requiere validación cruzada se obtuvo el valor del mejor  y el aRRMSE para la mejor configuración, sobre el conjunto de datos de entrenamiento. Se utilizó un conjunto de datos de prueba diferentes al de entrenamiento para medir el error de predicción al ejecutar cada algoritmo. La tabla 3 muestra los resultados de ejecutar cada algoritmo (filas) para las 12 bases de datos (columnas) midiendo el aRRMSE. En el caso de las variantes del algoritmo con validación cruzada se indica entre paréntesis el valor óptimo de K. De igual manera se aplica el test de Friedman tomando como hipótesis nula que el ranking promedios entre cada uno de los cuatro algoritmos es el mismo.

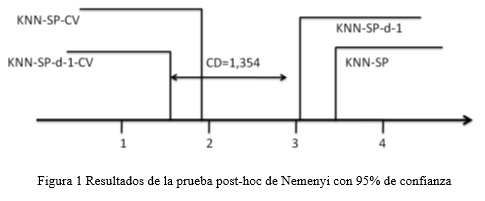
Los resultados del test de Friedman rechazan la hipótesis nula lo que indica que existen diferencias significativas entre los cuatro algoritmos. Al aplicar la prueba pos-hoc de Nemenyi se puede determinar el valor de la distancia crítica  con un 95  de confianza.

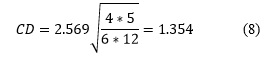
Como se puede apreciar en la figura 1 los resultados de la prueba post-hoc indican que existen diferencias significativas entre las variantes del algoritmo que utilizan el procedimiento de validación cruzada con respecto a las restantes.

 

CONCLUSIONES

Como conclusiones de la presente investigación podemos plantear que:

• De la documentación teórica analizada se identifica a la prueba no paramétrica de Friedman como las más utilizadas en el diseño de experimentos para validar algoritmos de aprendizaje automático.

• La aplicación del procedimiento de validación cruzada muestra mejores resultados en la experimentación del algoritmo KNN extendido para problemas de predicción con salidas compuestas.

• La aplicación de una prueba post-hoc de Nemenyi muestra que las variantes IBKMTRCV y IBKMTRCVW son significativamente mejores que cuando no es aplicado el procedimiento con un 95 de confianza.

 

REFERENCIAS BIBLIOGRÁFICAS

AHO, T., ŽENKO, B., DŽEROSKI, S., & ELOMAA, T. (2012). Multi-target regression with rule ensembles. The Journal of Machine Learning Research, 13(1), 2367–2407.

BORCHANI, H., VARANDO, G., BIELZA, C., & LARRAÑAGA, P. (2015). A survey on multi-output regression. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 5(5), 216–233.

COVER, T., & HART, P. (1967). Nearest neighbor pattern classification. Information Theory, IEEE Transactions on, 13(1), 21–27.

DEMŠAR, J. (2006). Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research, 7, 1–30.

FRIEDMAN, M. (1940). A comparison of alternative tests of significance for the problem of m rankings. The Annals of Mathematical Statistics, 11(1), 86–92.

GARCÍA, S., FERNÁNDEZ, A., LUENGO, J., & HERRERA, F. (2009). A study of statistical techniques and performance measures for genetics-based machine learning: accuracy and interpretability. Soft Computing, 13(10), 959–977.

GOLDWASSER, D., SRIKUMAR, V., & ROTH, D. (2012). Predicting structures in NLP: constrained conditional models and integer linear programming NLP. In Proceedings of the 2012 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies: Tutorials (p. 8). Association for Computational Linguistics.

LAM, M., RAO DOPPA, J., TODOROVIC, S., & DIETTERICH, T. G. (2015). HC-Search for structured prediction in computer vision. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 4923–4932.

NEMENYI, P. (1962). Distribution-free multiple comparisons. In Biometrics (Vol. 18, p. 263). INTERNATIONAL BIOMETRIC SOC 1441 I ST, NW, SUITE 700, WASHINGTON, DC 20005-2210.

NOWOZIN, S., GEHLER, P. V., JANCSARY, J., & LAMPERT, C. H. (2014). Advanced Structured Prediction. MIT Press.

PUGELJ, M., & DŽEROSKI, S. (2011). Predicting structured outputs k-nearest neighbours method. In Discovery Science (pp. 262–276). Springer.

SAVOJARDO, C., FARISELLI, P., MARTELLI, P. L., & CASADIO, R. (2013). Prediction of disulfide connectivity in proteins with machine-learning methods and correlated mutations. BMC Bioinformatics, 14(1), 1.

SPYROMITROS-XIOUFIS, E., TSOUMAKAS, G., WILLIAM, G., & VLAHAVAS, I. (2014). Drawing Parallels between Multi-Label Classification and Multi-Target Regression. arXiv Preprint arXiv:1211.6581v2.

TSOUMAKAS, G., SPYROMITROS-XIOUFIS, E., VILCEK, J., & VLAHAVAS, I. (2011). Mulan: A java library for multi-label learning. The Journal of Machine Learning Research, 12, 2411–2414.

YANG, W., WANG, K., & ZUO, W. (2013). Prediction of protein secondary structure using large margin nearest neighbour classification. International Journal of Bioinformatics Research and Applications, 9(2), 207–219

 

 

Recibido: 24/02/2016
Aceptado: 04/07/2016