Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.11 no.1 La Habana ene.-mar. 2017
ARTÍCULO ORIGINAL
Multiclasificador para predecir interacción de proteínas usando optimización basada en colonia de hormigas
Multi-classifier to predict protein interactions using ant colony optimization
Leidys Cabrera Hernández1*, Gonzalo Nápoles Ruiz1, Lester Santos Martínez 1, Gladys Casas Cardoso1, María M. García1
1Centro de Estudios de Informática, Universidad Central “Marta Abreu” de Las Villas, Carretera Camajuaní Km5 ½, Villa clara, Cuba. CP: 54830. {leidysc@uclv.edu.cu, gnapoles@uclv.edu.cu, lsantos@uclv.edu.cu, gcasas@uclv.edu.cu, mmgarcia@uclv.edu.cu}
*Autor para la correspondencia: leidysc@uclv.edu.cu
RESUMEN
En los últimos años el desarrollo de sistemas multi-clasificadores se ha convertido en un campo de investigación activo. Un sistema multi-clasificador es un conjunto de algoritmos de clasificación cuyas salidas individuales se funden para una mayor precisión. Muchos estudios teóricos y empíricos han demostrado las ventajas del paradigma de la combinación de clasificadores sobre los clasificadores individuales. Cuando se combinan clasificadores es importante garantizar la diversidad entre ellos de alguna manera, algunas medidas estadísticas pueden utilizarse para estimar la diversidad de un conjunto de clasificadores, estas se llaman medidas de diversidad. Otra cuestión a considerar es el número de clasificadores individuales incluidos en el modelo: cuanto menor sea el número de clasificadores, más simple es el sistema resultante. En términos generales, el principio de parsimonia es muy deseado en tales conjuntos, desde que un conjunto voluminoso también será un modelo que consume mucho tiempo. Encontrar el subconjunto mínimo de los clasificadores individuales que produce el mejor rendimiento del sistema se puede plantear como un problema de optimización combinatoria. En este trabajo se aborda el problema de la construcción de sistemas multi-clasificadores usando la Optimización basada en Colonia de Hormigas, un algoritmo de optimización meta heurístico ampliamente popular y eficaz, la razón principal detrás del uso del mismo radica en su fuerte capacidad para resolver problemas de optimización combinatoria entrelazados. Además, un análisis empírico es incluido para validar estadísticamente nuestra propuesta, mostrándose una aplicación real en la interacción de proteínas.
Palabras clave: multi-clasificador, clasificador, optimización de colonia de hormigas, medidas de diversidad.
ABSTRACT
In recent years the development of multi-classifier systems has become an active area research. A multi-classifier system is a set of classification algorithms whose individual outputs are fused for greater accuracy and interpretability. Many theoretical and empirical studies have shown the advantages of paradigm combination of classifiers over individual classifiers. When combined classifiers is important to ensure diversity among them in some way, some statistical measures can be used to estimate the diversity of a set classifiers, these are called diversity measures. Another issue to consider is the number of individual classifiers included in the model: the lower the number of classifiers, simpler is the resulting system. In general terms, the principle of parsimony is very desirable in such sets since a voluminous set also be a time-consuming model. Find the minimum subset of individual classifiers that produces the best system performance can pose as a combinatorial optimization problem. In this paper the problem of building multi-classifiers systems is addressed using Ant Colony Optimization, an optimization algorithm metaheuristic widely popular and effective, the main reason behind the use of it lies in its strong ability to solve problems intertwined combinatorial optimization. In addition, an empirical analysis is included to statistically validate our proposal, showing a real application in protein interaction.
Key words: multi-classifier, classifier, ant colony optimization, diversity measures.
INTRODUCCIÓN
Los problemas de clasificación son algunos de los temas más estudiados en la minería de datos y el aprendizaje automatizado. A pesar de la gran cantidad de documentos técnicos dedicados al tema, las técnicas de clasificación siguen ganando el apoyo firme de los investigadores en las disciplinas antes mencionadas. La elección del mejor clasificador depende en gran medida de las características del problema en cuestión y la naturaleza de los límites de decisión descubiertos por cada técnica para separar las diferentes clases de decisiones. En la búsqueda de mejores esquemas de clasificación, la combinación de varios clasificadores es una tendencia popular. Este es el punto crucial sobre el que se construye un multi-clasificador (MC). Un MC se basa en la combinación de un conjunto de clasificadores individuales a través de algunos criterios con la intención de lograr un resultado superior (Polikar, 2006). En principio, hay que esperar mejores resultados mediante el uso de un conjunto de clasificadores, incluso en problemas de clasificación de patrones complejos.
En (Dietterich, 2000) se sugieren tres tipos de razones por las cuales un sistema MC puede ser mejor que un clasificador simple. La primera es estadística, pues si efectivamente por cada clasificador tenemos una hipótesis, la idea de combinar estas hipótesis da como resultado una hipótesis que puede no ser la mejor, pero al menos evita seleccionar la peor de ellas. La segunda justificación es computacional, ya que algunos algoritmos ejecutan búsquedas que pueden llevar a diferentes óptimos locales: cada clasificador comienza la búsqueda desde un punto diferente y termina cercano al óptimo. Existe la expectativa de que alguna vía de combinación puede llevar a un MC a obtener una mejor aproximación. La última justificación es figurativa ya que es posible que el espacio de hipótesis considerado no contenga la hipótesis óptima; pero la aproximación de varias fronteras de decisión puede dar como consecuencia una nueva hipótesis fuera del espacio inicial y que se aproxime más a la óptima.
Como lo demuestra el número diverso de modelos disponibles en la literatura, hay varias maneras de desarrollar un MC. Algunas de ellas un poco más relacionadas con problemas de clasificación de patrones genéricos (por ejemplo, Bagging y Boosting), mientras que otras son con fines específicos. A pesar del campo de aplicación previsto para el modelo, la creación de MCs precisos implica dos retos principales. El primero está relacionado con la adecuada elección de los clasificadores individuales (es decir, los bloques de construcción) mientras que la segunda se centra en la combinación de sus salidas individuales de clasificación (Bonet, 2013).
La selección de los clasificadores bases es el primer paso en la construcción de un MC; hay varios modelos clásicos que se han propuesto para este fin. Bagging (Breiman, 1996) tiene sus raíces en el principio de la generación de diferentes conjuntos de entrenamiento extraídos del conjunto de entrenamiento inicial por medio de un muestreo aleatorio con reemplazo, lo que asegura la diversidad. Este modelo requiere la selección de un modelo débil o inestable de clasificación, es decir, un clasificador que varía sus salidas en presencia de, por ejemplo, cambios paramétricos menores. Bagging también asume que todos sus clasificadores débiles serán del mismo tipo o familia y la fusión de sus salidas individuales se lleva a cabo a través de la técnica de voto mayoritario. Este algoritmo puede ser aplicado en los métodos de aprendizaje con un atributo numérico de decisión (por ejemplo, problemas de regresión), en la que las salidas individuales son números reales y, por tanto, se promedian. Otra estrategia que Bagging emplea para producir el resultado final es estimar una probabilidad para cada salida. Estas probabilidades estimadas por los modelos se promedian y la clase más probable es la mostrada como solución por el modelo MC basado en Bagging (Witten, 2005).
Boosting (Schapire, 1990) es parecido a Bagging porque usa el método de crear bases de entrenamiento aleatorias con reemplazo, a partir de la base original y un único modelo de clasificación para los clasificadores de base, de ahí que la diversidad la garantice de la misma forma. Sin embargo, este algoritmo se realiza de manera secuencial, donde los clasificadores se van entrenando uno detrás del otro porque usan información del anterior. Otra diferencia es que Boosting le da un peso al modelo por su rendimiento, en lugar de dar peso igual a todos los modelos. El reemplazo se realiza estratégicamente de forma que los casos mal clasificados tienen mayor probabilidad, que los bien clasificados, de pertenecer al conjunto de entrenamiento del siguiente clasificador del sistema.
En resumen: las dos técnicas anteriores se limitan al mismo tipo de modelo de clasificación base y están capacitados con subconjuntos de sus datos de entrenamiento. El primer enfoque (Bagging) selecciona subconjuntos al azar, mientras que el segundo selecciona los subconjuntos de forma iterativa en base al resultado de la iteración anterior. Otro modelo que se denomina Stacking (Wolpert, 1992), es un método diferente a los anteriores pues la diversidad se determina con el empleo de diversos modelos de clasificación. Es menos utilizado que Bagging y Boosting, ya que es difícil de analizar teóricamente. Stacking combina múltiples clasificadores generados por diferentes algoritmos para un mismo conjunto de datos en una primera fase. Para combinar las salidas no utiliza voto mayoritario, sino que introduce un meta-clasificador que aprende la relación entre las salidas de los clasificadores de base y la clase original.
Se podría decir que estos tres paradigmas son los más generales y usados en la construcción de MCs, aunque la mejor alternativa no es fácil de determinar. Sistemas MCs, al igual que los clasificadores simples, no son intrínsecamente mejores que otros, pero tienen que ser seleccionados sobre la base de su rendimiento frente a un determinado tipo de problema (Kuncheva, 2004).
Algunos MCs aseguran la diversidad utilizando diferentes conjuntos de entrenamiento, pero esto sólo funciona para clasificadores que son sensibles a los cambios, tales como árboles de decisión. Otros utilizan diferentes conjuntos de rasgos y por lo tanto también varían los conjuntos de entrenamiento. Otros utilizan distintos tipos de clasificadores base, donde se hace muy necesario cuantificar la diversidad entre ellos.
Resulta intuitivo pensar que el resultado de combinar un grupo de clasificadores idénticos no va a ser mejor que el resultado de uno solo de sus miembros. Al contrario, resultaría más conveniente si combináramos un grupo de clasificadores diferentes entre sí, dado que al menos uno de ellos debe dar la respuesta correcta cuando el resto falle. Dicha diferencia, conocida principalmente como diversidad, también se le conoce como independencia, dependencia negativa o complementariedad. A pesar de que no existe una definición formal de lo que es intuitivamente percibido como diversidad, no al menos en el vocabulario de la Ciencia de la Computación, es ampliamente aceptado por la comunidad científica el hecho de que la existencia de diversidad en un grupo de clasificadores base es una condición necesaria para la mejora del desempeño de un ensamblado de clasificadores. Un ensamblado de clasificadores diversificados conduce a errores no correlacionados, que a su vez mejoran la precisión de clasificación (Shulklopert, 2012). Comprender y cuantificar la diversidad que existe en un ensamblado de clasificadores es un aspecto importante en la combinación de clasificadores. En la literatura existen diferentes medidas usadas para tal propósito, cuyo objetivo es cuantificar la dependencia existente entre clasificadores distintos, dichas medidas son conocidas como medidas de diversidad o diversity measures, las cuales se describen por Kuncheva y otros autores en (Kuncheva and Whitaker, 2003).
Otro aspecto a considerar es el número de clasificadores base que van a ser parte del MC: cuanto menor es el número de clasificadores, más simple es el sistema. Sin embargo, encontrar el subconjunto mínimo de clasificadores que sea también de alto rendimiento en el problema en cuestión, podría ser concebido como un problema de optimización combinatoria con un espacio de búsqueda exponencial; esto es debido al hecho de que la cantidad de combinaciones posibles entre los clasificadores crece a un ritmo bastante rápido. Incluso con un pequeño grupo de ellos podríamos terminar en un número muy explosivo de combinaciones posibles. Por ello, hemos decidido usar la Optimización basada en Colonia de Hormigas (OCH), un algoritmo meta heurístico, el cual ha demostrado ser una alternativa muy viable y robusta para hacer frente a las búsquedas complejas y problemas de optimización discretos (Bello et al., 2006, Nápoles et al., 2014) , gracias a su inspiración biológica y su naturaleza altamente paralelizado.
Por los hechos antes mencionados, en este trabajo se presenta una nueva formulación para el aprendizaje de un MC por medio de la meta-heurística OCH. En particular OCH ayuda en la selección de un grupo adecuado de clasificadores base de un gran número de alternativas posibles. Además, se asegura que este grupo posea una buena diversidad y alcance la más alta precisión posible de la clasificación para el problema en cuestión.
MATERIALES Y MÉTODOS
En este apartado, se presenta la formulación de algunas medidas de diversidad existentes en la literatura para medir cuán diverso puede ser un conjunto de clasificadores, también se describe la formulación de OCH para la generación automática de un MC que garantice la diversidad en el conjunto de solución, así como la más alta precisión posible en la clasificación.
Medidas de diversidad
Estas medidas para cuantificar la diversidad, pueden ser categorizadas en dos tipos: medidas de pareja (pairwise) y medidas de grupo (non pairwise). A continuación, veremos las medidas por pareja ya que estas son las que contiene mejor interpretabilidad y una fácil formulación matemática, razones por las cuales fueron seleccionadas para este trabajo.
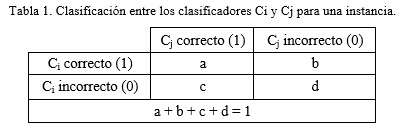
Las medidas de pareja se calculan por pares de clasificadores usando sus salidas, las cuales son binarias (1,0) que indica si la instancia fue correctamente clasificada o no por el clasificador. A continuación, se indica en la Tabla 1 el resultado de dos clasificadores (Ci, Cj) para una instancia en cuanto a si la clasificaron correctamente o no. El valor de a es igual a 1 si ambos clasificadores son correctos en la clasificación, si ambos se equivocan entonces d es igual a 1, mientras que los valores de b y c solo toman valor 1 en caso de que uno de los clasificadores sea correcto y el otro no. Para una instancia la suma de estos valores solo puede ser igual a 1, ya que solo uno de los casos anteriores podrá ocurrir.
Si se suman entonces los valores de a, b, c y d obtenidos para todas las instancias entre el par de clasificadores (Ci, Cj) se obtendrá el resultado mostrado en la Tabla 2, donde A representa la suma de las instancias en que ambos clasificadores fueron correctos, D es la suma de las instancias donde ambos se equivocaron, mientras que B y C representan la cantidad de instancias en las que uno fue correcto y el otro no, a partir de estos valores se calculan entonces las medidas en forma de pares.
Es decir, A sería igual a la suma total de los valores de a para todas las instancias y así respectivamente con los valores de B, C y D.
La suma total de A, B, C y D entonces es igual a N, que tiene que coincidir con el número total de instancias o casos.
Un conjunto de L clasificadores produce L*(L-1)/2 pares de valores. Para obtener un único resultado habría que promediar estos valores.
Coeficiente de correlación ρ
El coeficiente de correlación (Kuncheva, 2004) entre dos clasificadores Ci y Cj se calcula como:
![]()
El valor final de la medida para un conjunto de clasificadores sería el promedio de los valores asociados a cada combinación de dos clasificadores que se extraiga del conjunto. Mientras menor sea el valor de ρ, mayor será la diversidad. Los valores estarán en el intervalo [-1, 1].
Estadístico Q
El estadístico Q se calcula de la siguiente forma:
![]()
Se ha demostrado que ρ y Q tienen el mismo signo. Además, se puede demostrar que |ρ| ≤ |Q|.(Kuncheva and Whitaker, 2003)
Medida de desacuerdo
La medida de desacuerdo fue introducida por (Skalak, 1996), es la más intuitiva de las medidas entre un par de clasificadores, y es igual a la probabilidad de que los dos clasificadores discrepen en sus predicciones. Mientras mayor sea su valor mayor será la diversidad.
![]()
Medida de Doble Fallo
La medida de doble fallo fue introducida por (Giacinto, 2001) y considera el fallo de los dos clasificadores al mismo tiempo. En (Ruta, 2001) definen a esta medida como una medida no-simétrica, esto quiere decir que si se intercambian los unos con los ceros en los resultados de los clasificadores, el valor de la medida no va a ser el mismo. Esta medida está basada en el concepto de que es más importante conocer cuándo errores simultáneos son cometidos que cuándo ambos tienen clasificación correcta. Mientras menor sea el valor mayor será la diversidad.
![]()
Optimización de Colonia de Hormigas
La meta heurística OCH es un método de búsqueda estocástica diseñado originalmente en los problemas de optimización combinatoria; este método fue inventado por Marco Dorigo y se inspira en una colonia de hormigas (Escalona et al., 2005). Las hormigas reales en la naturaleza, buscan los alimentos en la proximidad de su nido al azar. Una vez que las hormigas han encontrado una fuente de alimento, evalúan esta fuente de acuerdo a su calidad y cantidad. En el camino de vuelta al nido, ponen una sustancia química llamada feromona en el suelo con el fin de guiar al resto de la colonia a la fuente de alimentación (Dorigo, 2000). Por lo tanto, OCH es un modelo totalmente constructivo, donde cada hormiga construye gradualmente una solución candidata al problema mediante la exploración de un gráfico construido de una manera paso a paso. Más específicamente, cada hormiga artificial pasa de un estado (vértice o nodo del gráfico) a otro durante el proceso de búsqueda. La solución es entonces una secuencia de movimientos. La preferencia de movimiento depende de dos valores asociados al enlace (aristas o arcos del gráfico) entre estos dos nodos: La información artificial denotada por ![]() se basa directamente en los rastros de feromona de ir del nodo i al nodo j, y las hormigas la actualizan de forma iterativa durante la ejecución del algoritmo y la información heurística
se basa directamente en los rastros de feromona de ir del nodo i al nodo j, y las hormigas la actualizan de forma iterativa durante la ejecución del algoritmo y la información heurística ![]() indica la preferencia heurística de moverse desde el nodo i hasta el nodo j, o sea de recorrer la arista. Este aspecto específico del problema del conocimiento a menudo no se modificará durante la ejecución del algoritmo, por lo que debe ser estimada cuidadosamente.
indica la preferencia heurística de moverse desde el nodo i hasta el nodo j, o sea de recorrer la arista. Este aspecto específico del problema del conocimiento a menudo no se modificará durante la ejecución del algoritmo, por lo que debe ser estimada cuidadosamente.
En cada paso de construcción, una hormiga k escoge ir al siguiente nodo con una probabilidad que se calcula como la ecuación (5), la cual indica la probabilidad de aceptar el estado j-ésimo, en la posición i-ésima del candidato que le corresponde, ![]() es el conjunto de estados no visitados para la hormiga k-ésima, mientras que
es el conjunto de estados no visitados para la hormiga k-ésima, mientras que ![]() y
y ![]() son dos parámetros que se utilizan para el control de la influencia ejercida por los rastros de feromona y la información heurística, respectivamente, sobre la probabilidad de transición.
son dos parámetros que se utilizan para el control de la influencia ejercida por los rastros de feromona y la información heurística, respectivamente, sobre la probabilidad de transición.

Una vez completado el proceso iterativo de construcción de solución, todos los rastros de feromona son actualizados utilizando las soluciones construidas por las hormigas. En la primera etapa de evaporación de feromonas se lleva a cabo lo que reduce uniformemente la cantidad de feromona establecida en todos los caminos por una cierta cantidad. Posteriormente, una o más soluciones se utilizan para aumentar el valor de feromonas de los caminos incluidos en estas soluciones. El esquema de actualización de feromona es un paso fundamental en cualquier algoritmo basado en OCH. Esencialmente, las variantes de OCH difieren principalmente en la estrategia usada para actualizar el rastro de feromona en cada iteración.
Sistema de Hormigas
El Sistema de Hormigas (SH) fue el primer algoritmo de OCH propuesto (Morales, 2014). En SH, los rastros de feromona son actualizados una vez que todas las hormigas han completado sus recorridos. Como un primer paso, todos los rastros de feromona se evaporan de manera uniforme utilizando un factor constante ![]() Después de eso, cada hormiga deposita una cantidad de feromona
Después de eso, cada hormiga deposita una cantidad de feromona ![]() en las aristas del gráfico, que son parte de su solución. Se debe mencionar que el valor
en las aristas del gráfico, que son parte de su solución. Se debe mencionar que el valor ![]() se calcula de acuerdo con la calidad de la solución encontrada por la k-ésima hormiga. La siguiente ecuación resume los dos pasos, donde ρ indica la tasa de evaporación, mientras que P es el número de hormigas en la colonia.
se calcula de acuerdo con la calidad de la solución encontrada por la k-ésima hormiga. La siguiente ecuación resume los dos pasos, donde ρ indica la tasa de evaporación, mientras que P es el número de hormigas en la colonia.
![]()
En los caminos (aristas) que no son elegidos periódicamente por las hormigas, los niveles de feromonas asociados disminuirán gradualmente con el número de iteraciones, mientras que los caminos a menudo seleccionados por las hormigas verán su nivel de feromona reforzado, por lo tanto, haciéndolos más propensos a ser seleccionados en futuras iteraciones. Sin embargo, las simulaciones más completas reportadas en (Cisneros Matos, 2007) describen que los mejores resultados se podrían lograr si sólo se utiliza la mejor solución global para la actualización de los rastros de feromona en lugar de utilizar todas las hormigas en la colonia. Observe que la acumulación ilimitada de feromona en los caminos más prometedores puede producir un estancamiento en la búsqueda.
Sistema de Colonia de Hormigas
Sistema de Colonia de Hormigas (SCH) se diseñó para mejorar el método SH explotando las mejores soluciones globales encontradas por las hormigas durante la etapa de búsqueda (Machado Tugores, 2013). Como resultado de ello, el algoritmo mejora las características de explotación de las hormigas cuando construyen una solución en vez de explorar nuevas áreas del espacio de soluciones. Este objetivo se logra a través de tres mecanismos: (1) una fuerte estrategia elitista para la actualización de rastros de feromonas; (2) una regla para la actualización de rastros de feromona durante la fase de búsqueda, y (3) una regla de probabilidad de transición pseudo-aleatoria. La ecuación (7) formaliza la estrategia para la actualización de los rastros de feromona, donde ![]() indica la cantidad de feromona asociada con la hormiga que tiene el mejor valor heurístico. Esto significa que la etapa de evaporación se lleva a cabo en todos los caminos (aristas), como en SH, pero el proceso de actualización sólo se produce en el camino descubierto por el mejor individuo.
indica la cantidad de feromona asociada con la hormiga que tiene el mejor valor heurístico. Esto significa que la etapa de evaporación se lleva a cabo en todos los caminos (aristas), como en SH, pero el proceso de actualización sólo se produce en el camino descubierto por el mejor individuo.
![]()
Con el fin de aprovechar plenamente el mejor conocimiento provocado por las hormigas en su viaje, SCH también introduce una regla proporcional pseudo-aleatoria (véase la ecuación (8)). Más específicamente, una decisión aleatoria se hace con probabilidad q0 para moverse al nodo que contenga el producto máximo de rastros de feromona y la información heurística; de lo contrario SCH adoptará la regla de decisión estándar ofrecida por SH. El valor q0 es un parámetro que debe ser fijado por el experto a priori; cuando se aproxima a 1, la explotación se ve favorecida por la exploración.

Por último, en el modelo SCH, las hormigas utilizan una regla adicional para la actualización de los rastros de feromonas cuando están construyendo la solución candidata, como se muestra en la ecuación (9). Este enfoque tiene el mismo efecto de disminuir la probabilidad de seleccionar la misma ruta de acceso para todas las hormigas; Por lo tanto, combate el problema de estancamiento presente en SH, dado que introduce un equilibrio entre la explotación y la exploración.
![]()
Sistema de Hormigas MAX-MIN
El Sistema de Hormigas MAX-MIN (SHMM) fue desarrollado específicamente para promover una explotación más fuerte de las soluciones y por lo tanto evitar caer en un estado de estancamiento (Machado Tugores, 2013). En pocas palabras, podríamos definir un estado de estancamiento como la situación en la que las hormigas construyen la misma solución una y otra vez y, finalmente, la exploración se detiene. Este modelo tiene las siguientes características: Igualmente a SCH, una fuerte estrategia elitista regula el agente autorizado a actualizar los rastros de feromona. Podría ser la hormiga que tiene la mejor solución hasta el momento, o el que tiene la mejor solución en la iteración actual. En segundo lugar, todos los rastros de feromona se limitan al rango ![]() para todos los componentes de la solución, entonces la probabilidad de la selección de un estado específico nunca será cero, lo que evita configuraciones de estancamiento. Como punto final, rastros de feromona se inicializan con
para todos los componentes de la solución, entonces la probabilidad de la selección de un estado específico nunca será cero, lo que evita configuraciones de estancamiento. Como punto final, rastros de feromona se inicializan con ![]() para garantizar una mayor exploración del espacio de búsqueda en el comienzo de la fase de optimización.
para garantizar una mayor exploración del espacio de búsqueda en el comienzo de la fase de optimización.
Las tres variantes de OCH descritas anteriormente fueron tenidas en cuenta para nuestro problema.
Construcción de un multi-clasificador con OCH
A continuación, se aborda el problema de la construcción de un MC "óptimo" mediante el uso de la meta-heurística OCH. Aquí, el criterio de optimalidad se refiere a la precisión del sistema final y al número de clasificadores base seleccionados. Ciertamente, no podemos asegurar que nuestra propuesta será siempre encontrar el óptimo global porque el optimizador seleccionado (OCH) puede converger a una solución sub-óptima. Sin embargo, hemos adoptado esta meta-heurística ya que es capaz de encontrar soluciones casi óptimas en un tiempo de ejecución razonablemente corto, sin imponer ningunas limitaciones sobre la función objetivo (por ejemplo, la continuidad, diferenciabilidad, convexidad o información gradiente) que rara vez se conocen de antemano.
Supongamos una familia de clasificadores ![]() donde cada clasificador tiene un error de clasificación asociado
donde cada clasificador tiene un error de clasificación asociado ![]() donde
donde ![]() indica la clasificación del problema a resolver. La cuestión de la construcción de un MC M consiste en encontrar un subconjunto de estos clasificadores
indica la clasificación del problema a resolver. La cuestión de la construcción de un MC M consiste en encontrar un subconjunto de estos clasificadores ![]() con la diversidad máxima de tal manera que
con la diversidad máxima de tal manera que ![]() tienda al error mínimo. Note que
tienda al error mínimo. Note que ![]() necesariamente debe ser estrictamente menor que
necesariamente debe ser estrictamente menor que ![]() , de lo contrario la solución será el trivial (por ejemplo, todos los clasificadores individuales se incluyen en el conjunto). Por otra parte, el modelo tiene que cumplir con otro obstáculo:
, de lo contrario la solución será el trivial (por ejemplo, todos los clasificadores individuales se incluyen en el conjunto). Por otra parte, el modelo tiene que cumplir con otro obstáculo: ![]() está el mejor clasificador incluido en el conjunto. Esta restricción asegura que el conjunto mejora el rendimiento de la clasificación sobre cualquiera de sus esquemas de clasificación constituyentes.
está el mejor clasificador incluido en el conjunto. Esta restricción asegura que el conjunto mejora el rendimiento de la clasificación sobre cualquiera de sus esquemas de clasificación constituyentes.
Desde el punto de vista de la optimización, las soluciones candidatas para nuestro problema pueden ser codificados como un vector binario en el que el estado "1" en la i-ésima dimensión significa que el clasificador ![]() se incluirá en el conjunto, mientras que el estado "0" indica que
se incluirá en el conjunto, mientras que el estado "0" indica que ![]() no será ser incluido en M. Por lo tanto, el modelo propuesto
no será ser incluido en M. Por lo tanto, el modelo propuesto ![]() representa la probabilidad de asignar el estado
representa la probabilidad de asignar el estado ![]() a la i-ésima dimensión (es decir, la probabilidad de incluir el clasificador i-ésimo). La ecuación (10) da a conocer la función objetivo que debe minimizarse durante el proceso de búsqueda llevado a cabo por OCH, donde X es la solución candidata, Mx denota el conjunto calculado a partir de X y
a la i-ésima dimensión (es decir, la probabilidad de incluir el clasificador i-ésimo). La ecuación (10) da a conocer la función objetivo que debe minimizarse durante el proceso de búsqueda llevado a cabo por OCH, donde X es la solución candidata, Mx denota el conjunto calculado a partir de X y ![]() denota su error de clasificación. En esta formulación, un factor
denota su error de clasificación. En esta formulación, un factor ![]() se introduce con el fin de controlar la relevancia que el experto otorga a la precisión del sistema con respecto a la cardinalidad del conjunto, es decir, el número de clasificadores seleccionados.
se introduce con el fin de controlar la relevancia que el experto otorga a la precisión del sistema con respecto a la cardinalidad del conjunto, es decir, el número de clasificadores seleccionados.
![]()
Durante el proceso de búsqueda, las soluciones que tienen una tasa de error mayor que la tasa de error asociada al mejor clasificador incluido en el conjunto (es decir, ![]() deben ser penalizadas por un factor positivo. Además, dos soluciones no factibles pueden inducir errores diferentes, y por lo tanto la estrategia de penalización debe considerar este hecho cuando se adapte la función objetivo F(X). Por ejemplo, consideremos dos soluciones diferentes
deben ser penalizadas por un factor positivo. Además, dos soluciones no factibles pueden inducir errores diferentes, y por lo tanto la estrategia de penalización debe considerar este hecho cuando se adapte la función objetivo F(X). Por ejemplo, consideremos dos soluciones diferentes ![]() que codifican los
que codifican los ![]() conjuntos, respectivamente. Si los errores inducidos
conjuntos, respectivamente. Si los errores inducidos ![]() son mayores que cero, entonces X1 y X2 son ambos considerados no factible. Sin embargo, es poco probable que E1 - E2 = 0. Esto sugiere que no debemos penalizar a ambas soluciones con el mismo valor positivo; en cambio, debemos penalizar a cada solución en función de su error
son mayores que cero, entonces X1 y X2 son ambos considerados no factible. Sin embargo, es poco probable que E1 - E2 = 0. Esto sugiere que no debemos penalizar a ambas soluciones con el mismo valor positivo; en cambio, debemos penalizar a cada solución en función de su error ![]() En este trabajo, hacemos uso de una función de penalización dinámica P(X) que tiene en cuenta el error inducido como sigue:
En este trabajo, hacemos uso de una función de penalización dinámica P(X) que tiene en cuenta el error inducido como sigue:

Otro aspecto que hay que considerar cuando se resuelve un problema de optimización combinatorio mediante cualquier algoritmo de OCH es la estimación de la información heurística. Este componente permite mejorar la búsqueda, incluso en grandes espacios de búsqueda, ya que corresponde a los conocimientos específicos del problema la incorporación de la regla de probabilidad de transición de estado. Como se mencionó en la introducción los clasificadores que inducen gran diversidad tienden a mejorar el rendimiento del conjunto global, incluso cuando no son los más precisos. La ecuación (12) formaliza este razonamiento al estimar la matriz heurística ![]() donde D epresenta la diversidad del conjunto en consideración,
donde D epresenta la diversidad del conjunto en consideración, ![]() se refiere a la familia de los clasificadores base y el índice j indica el estado del clasificador i-ésimo (0 = excluido, 1 = incluido) en el conjunto.
se refiere a la familia de los clasificadores base y el índice j indica el estado del clasificador i-ésimo (0 = excluido, 1 = incluido) en el conjunto.
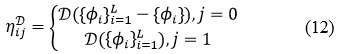
Es importante recordar que la diversidad anterior se calcula usando las medidas de diversidad enunciadas en el primer epígrafe.
RESULTADOS Y DISCUSIÓN
Para validar empíricamente la metodología propuesta en este estudio se diseñaron varios experimentos para conocer el comportamiento de nuestro MC construido basado en OCH. El MC fue generado usando el mecanismo de Vote el cual permite la combinación de distintos tipos de modelos bases, los cuales fueron tomados de la herramienta WEKA, en donde tienen los siguientes nombres: Árbol de decisión alternativo ADTree, J48, Logistic function, K-Nearest Neighbor, Naïve Bayes y Multi-Layer Perceptron (MLP). Dos estrategias fueron consideradas para combinar las salidas de los clasificadores bases: promedio y voto mayoritario. Todos los experimentos fueron realizados con la siguiente configuración para la meta-heurística OCH: 50 iteraciones, constante de evaporación ρ = 0.9; ACS’ phi = 0.9 y q0 = 0.7. El conjunto de datos fue dividido en dos grupos, 66% de las instancias para entrenar y el resto para evaluación. Se usaron 10 bases de datos del Repositorio de Aprendizaje Automático de la Universidad de California Irvine (en inglés UCI MLR), ver Tabla 3.
Los experimentos estuvieron encaminados a identificar cuáles de las variantes modeladas de OCH obtiene los mejores resultados. Se crearon dos grupos basados en la cantidad de clasificadores en los conjuntos de solución, grupo 1: contiene aquellas soluciones que tienen 2 o 3 clasificadores y el grupo 2: contiene aquellas soluciones con una cantidad de clasificadores mayor a 3. Se define el primer grupo con soluciones que incluyen solo hasta 3 clasificadores, siendo dicha cantidad un umbral empírico establecido en los experimentos, debido a que el número máximo de clasificadores incluidos en las soluciones es 6, por lo tanto pensamos que las combinaciones menos complejas eran aquellas que solo incluían pocos clasificadores, siendo estas aquellas que tienen la cantidad mínima posible (2) y 3.
De esta manera el grupo 1 representa las soluciones obtenidas con menor cantidad de clasificadores y por tanto las soluciones menos complejas, mientras que el grupo 2 representa las más complejas, en función por supuesto de la cantidad de clasificadores incluidos en el MC. Luego se aplicó la prueba estadística Chi-cuadrado, la cual reveló la existencia de diferencias significativas entre las variantes. Como se puede observar en la Tabla 4 la variante SHMM muestra la mayor cantidad de casos en el primer grupo, es decir, las soluciones que menor número de clasificadores tienen se encuentran usando esta variante.
Adicionalmente se aplicó la prueba de Kruskal-Wallis para determinar la variante que ofrece los mejores resultados en cuanto a la exactitud de la clasificación. Esta prueba reveló que no existían diferencias significativas, lo cual se muestra en la Tabla 5, aunque se puede observar en ella que el valor más alto en el rango promedio de los valores obtenidos se alcanza con la variante SHMM. Por tanto, se sugiere el uso de esta variante por los resultados obtenidos.
Interacción de proteínas en la Arabidopsis thaliana
El problema consiste en predecir interacciones de proteínas en una base de datos de Arabidopsis thaliana, la base se obtuvo en el Departamento de Biología de Sistemas de Plantas del Instituto de Biotecnología (VIB) en Bélgica. Dicha base contiene información relevante de las interacciones de proteínas de la Arabidopsis thaliana: atributos de dominios conservados, valores de expresión para calcular coeficientes de correlación Pearson, información de anotaciones de genes ontólogos, grupos ortólogos, entre otros. El conjunto de datos consta de 4314 pares de proteínas, 1438 son ejemplos de verdaderas interacciones y 2876 son ejemplos negativos (o al menos dudosos). Los resultados reportados anteriormente demuestran que identificar simultáneamente ejemplos positivos y negativos resulta difícil, pues es raro encontrar reportes de pares de proteínas que no interactúan, especialmente a gran escala y los casos negativos para el aprendizaje no son del todo seguros. Se seleccionaron en total 11 rasgos, más la variable especial denominada clase, la cual identifica si hay o no una interacción de proteína. Los clasificadores bases fueron los mismos mencionados en el experimento, así como la misma configuración para la meta-heurística, usando ahora solo la variante SHMM la cual arrojó los mejores resultados, la medida de diversidad usada fue Doble-Fallo. El mejor clasificador individual presentó una exactitud igual a 0.82 en el caso de J48, a continuación se muestra en la Tabla 6 la solución obtenida con su exactitud y diversidad correspondiente, las posiciones con “1” en la solución corresponden con los clasificadores incluidos en el conjunto, en este caso: Logistic function, J48 y MLP. La posición señalada en rojo corresponde con la del mejor clasificador individual lo cual significa que está incluido en la solución del MC.
CONCLUSIONES
En este trabajo se describe cómo construir un MC usando la meta-heurística OCH. En particular tres populares variantes de ella han sido tenidas en cuenta. Se describe la función objetivo y la función heurística usada, la cual tiene en cuenta la diversidad del conjunto según las medidas de diversidad. Los experimentos confirman que los mejores resultados se obtienen con la variante SHMM, garantizándose la existencia de diversidad en el conjunto de clasificadores y los mejores grados de clasificación posible. Luego se muestra una aplicación real para probar el desempeño del MC para predecir la interacción de proteínas en la Arabidopsis thaliana, donde la exactitud del mejor clasificador individual es superada en 4% por el MC.
REFERENCIAS BIBLIOGRÁFICAS
BREIMAN, L. 1996. Bagging predictors. Machine Learning, 24, 123-140.
ESCALONA, J. C., CARRASCO, R. & PADRÓN, J. A. 2005. Introducción al diseño de Fármacos
SCHAPIRE, R. E. 1990. The strength of weak learnability. Machine Learning, 5, 197-227.
WOLPERT, D. 1992. Stacked generalization. Neural Networks, 5, 241-259.
Recibido: 25/08/2016
Aceptado: 02/11/2016