Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.11 no.4 La Habana oct.-dic. 2017
ARTÍCULO ORIGINAL
Implementación en VHDL de Procesador de Promediación Adaptado a Cambios Estadísticos en Clutter Weibull
VHDL Implementation of a Clutter Averaging Processor Adapted to Statistical Changes in Weibull Clutter
José Raúl Machado Fernández1*, Edgardo Fernández Giquel1, Roberto Carlos Sánchez Rams1, Jesús de la Concepción Bacallao Vidal1
1 Facultad de Eléctrica, Departamento de Telecomunicaciones y Telemática, Universidad Tecnológica de La Habana, Cuba. {rsanchezr, bacallao}@electrica.cujae.edu.cu
*Autor para la correspondencia: m4ch4do@hispavista.com
RESUMEN
La cancelación de los efectos perjudiciales causados por la señal de clutter está entre los principales problemas que presentan los detectores de radar actuales. Específicamente, la variación estadística lenta del clutter hace que el detector de promediación de celdas (CA-CFAR) vea su probabilidad de falsa alarma operacional desviada del valor concebido en el diseño. Para corregir este problema, los autores desarrollaron una mejora del CA-CFAR que rectifica continuamente el factor de ajuste, a partir de estimaciones realizadas con el método de los momentos y expresiones matemáticas tomadas de estudios recientes. La solución se implementó en VHDL para su aplicación directa en instalaciones operativas. Conjuntamente, se construyó el esquema en MATLAB, hecho que permitió validar los resultados por comparación con lo obtenido en VHDL. El nuevo detector, denominado W-MoM-CA-CFAR, contribuye al desarrollo de la teoría de los detectores de radar, a la vez que busca mejorar el parque de radares cubanos.
Palabras clave: Probabilidad de Falsa Alarma, Método de los Momentos, VHDL, CA-CFAR, Clutter de Radar, Distribución Weibull.
ABSTRACT
The cancellation of the undesired effects caused by the clutter signal is among the main problems faced by today’s radar detectors. The clutter slow statistical variations usually force the false alarm probability of the CA-CFAR detector to deviate from the design value. The authors developed an enhanced CA-CFAR which continually corrects its adjustment factor by performing estimations with the method of moments and applying mathematical expressions taken from recent studies. The solution was implemented in VHDL for its direct application in operational systems. In addition, the scheme was reproduced on MATLAB, which allowed to validate the results by comparing with the VHDL output. The new detector, called W-MoM-CA-CFAR, contributes to the development of radar detectors theory, and seeks to improve Cuban radar systems.
Key words: False Alarm Probability, Method of Moments, VHDL, CA-CFAR, Radar Clutter, Weibull Distribution
INTRODUCCIÓN
La labor de los radares activos consiste en detectar blancos dentro del área de observación y estimar parámetros básicos como la posición y la velocidad (Madisetti, 2010). La detección es una tarea fácil cuando los objetivos están ubicados en un medio no reflector, porque los ecos captados en el receptor son producto estrictamente del rebote de las ondas electromagnéticas en la superficie del blanco. En dicho caso, los retornos pueden ser comparados con un umbral fijo, señalándose la existencia de blancos cuando las lecturas superan cierto umbral predeterminado (Kouemou, 2009).
No obstante, en ambientes de operación reales aparece una señal interferente llamada clutter que se superpone a la información del blanco y del ruido térmico, superando comúnmente la magnitud de este último (Richards, et al. 2010). El clutter es el resultado del rebote de la emisión del radar en el fondo donde está contenido el blanco. Dos de los fondos más comunes encontrados son el clutter terrestre y el clutter marino (Skolnik, 2008). Generalmente el clutter marino presenta un nivel de interferencia superior al terrestre, por lo que los radares que operan en ambientes de mar tienen una seria limitación en su desempeño impuesta por los ecos indeseados (Watts, 1987).
La modelación matemática del clutter es la de una variable aleatoria continua cuya Función de Densidad de Probabilidad (PDF, Probability Density Function) contiene regularmente entre uno y tres parámetros (Cai, et al. 2009; Cai, et al. 2010; Ishii, et al. 2011; Ollila, et al. 2012; Weiping, et al. 2013) . Los modelos más populares son el Log-Normal (Farina, et al. 1986; Ward, et al. 2013), el Weibull (Chan, 1990; Chen et al. 2013) y el K (Raghavan, 1991; Sayama and Ishii, 2013).
Cuando se diseñan detectores para blancos de radar embebidos en clutter, se utiliza el conocido teorema de Neyman-Pearson, según el cual se busca garantizar un cierto valor de probabilidad de falsa alarma ![]() y luego intentar mejorar al máximo la probabilidad de detección
y luego intentar mejorar al máximo la probabilidad de detección ![]() . Así, los mecanismos de discriminación de clutter más populares son los denominados CFAR (Constant False Alarm Rate, Tasa de Falsa Alarma Constante) porque aseguran que la detección ocurra bajo la garantía de una falsa alarma constante (Skolnik, 2008).
. Así, los mecanismos de discriminación de clutter más populares son los denominados CFAR (Constant False Alarm Rate, Tasa de Falsa Alarma Constante) porque aseguran que la detección ocurra bajo la garantía de una falsa alarma constante (Skolnik, 2008).
En la literatura pueden encontrarse varios tipos de algoritmos CFAR basados en un mecanismo de ventana deslizante. Las variantes clásicas son el CA-CFAR (Cell Averaging CFAR, Promediación de Clutter), el GO-CFAR (Greatest-Of CFAR, Mayor-de), el SO-CFAR (Smallest-Of CFAR, Menor-de) y el OS-CFAR (Ordered Statistics CFAR, Estadística Ordenada). Dichos detectores han sido tratados por varios autores (Farina and Studer, 1986; Rohling, 1983; Weingberg, 2004) y son frecuentemente usados como referencia en investigaciones actuales (Caso and De Nardis, 2013; de Figueiredo, 2013; Qin and Gong, 2013; Takahashi, 2010) . La mayoría de las variantes de CFAR tienen en común que permiten el ajuste de la probabilidad de falsa alarma mediante un factor de escala o ajuste (T), modificando en una relación inversa el nivel de probabilidad de detección (Farina and Studer, 1986; Rohling, 1983).
Motivación
El Grupo de Investigación de Radares del Instituto Superior Politécnico José Antonio Echeverría (ISPJAE-CUJAE) está enfocado en el desarrollo de detectores de radar basados en algoritmos de estimación novedosos como son la detección con el empleo de momentos de alto orden (Bacallao Vidal, 2003; Guillén Soriano, 2013) y la aplicación de las redes neuronales artificiales (Machado Fernández and Bacallao Vidal, 2016; Machado Fernández, et al. 2015).
En Machado Fernández and Bacallao Vidal (2014) el grupo encontró y caracterizó un problema que afecta al detector CA-CFAR. Si ocurren variaciones estadísticas lentas en el clutter, la probabilidad de falsa alarma operacional se alejará de la de diseño porque el sistema es incapaz de adaptarse a un fondo cambiante. Luego, en (Machado Fernández, 2015b) se presentó la alternativa W-MoM-CA-CFAR que reduce significativamente la desviación utilizando el método de los momentos (MoM, Method of Moments) para estimar el parámetro de forma del clutter distribuido Weibull (W). Dado que la suposición Weibull está entre las más aceptadas en la literatura, el W-MoM-CA-CFAR utilizó las expresiones matemáticas dadas en (Machado Fernández, 2015a) para transformar la estimación en un valor viable del factor de ajuste, completando así el diseño.
Dado el éxito de la solución, los autores de la presente investigación se trazaron como objetivo la implementación del W-MoM-CA-CFAR en VHDL (Very high speed integrated circuit Hardware Description Language, Lenguaje de Descripción de Hardware para circuitos integrados de muy alta velocidad) para su posterior implementación en ambientes operacionales. Tomando como partida el aporte de (Machado Fernández and Sánchez Rams, 2016), los autores completaron la implementación y validaron su funcionamiento por comparación con un esquema similar que crearon en MATLAB. El diseño de esta variante mejorada contribuye a la modernización de los radares cubanos y ofrece una solución viable a una de las problemáticas actuales de los procesadores CFAR.El artículo tiene la siguiente estructura. La segunda sección titulada “Materiales y Métodos” describe el detector W-MoM-CA-CFAR y da detalles sobre la arquitectura construida en VHDL. La tercera sección bajo el nombre de “Resultados y Discusión” ofrece evidencia del correcto funcionamiento del procesador, enfocándose en la estimación de la media y la varianza, y su influencia en el proceso. Por último, en “Conclusiones y Trabajo Futuro” se resumen los aportes fundamentales del documento y se indican las líneas por la que puede continuarse la investigación.
MATERIALES Y MÉTODOS
La presente sección se divide en dos epígrafes. El primero presenta la versión clásica del detector CA-CFAR junto a las modificaciones introducidas para convertir el esquema en el W-MoM-CA-CFAR. El segundo epígrafe hace una breve referencia a los puntos fundamentales de la implementación VHDL.
Detector W-MoM-CA-CFAR
El detector W-MoM-CA-CFAR consiste en la adición de un Esquema Corrector del Factor de Ajuste a la variante clásica CA-CFAR. Así, el CA-CFAR mantiene su modo de operación tradicional con la única diferencia de que el factor de ajuste será corregido continuamente con cada nueva muestra adquirida. Los autores asumieron que el clutter de fondo procesado se correspondía con la distribución Weibull cuya función de densidad de probabilidad es (González Padilla, et al. 2013):
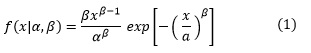
Donde α es el parámetro de escala y β es el de forma.
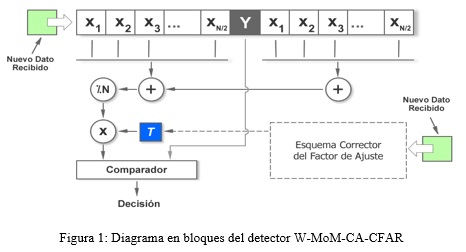
Según se observa en la figura 1, el detector de promediación de celdas consiste en una ventana deslizante que se desplaza por toda la región de cobertura, de modo que cada célula resolutiva tiene una oportunidad de ocupar la región Y que está bajo evaluación. Se decide si existe un blanco en Y comparando con un umbral de detección que se obtiene multiplicando el promedio de las celdas vecinas (X) por el factor de ajuste (T). El presente proyecto asumió un tamaño de ventana igual a 64(N=64), lo que representa una selección frecuente.
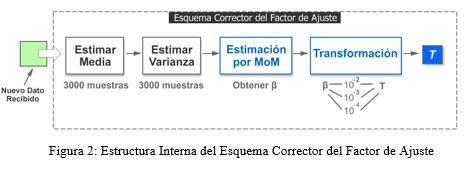
La figura 2 muestra los bloques que componen el Esquema Corrector del Factor de Ajuste. La solución trabaja con un número de muestras superior al almacenado en la ventana. En este caso, siguiendo las recomendaciones de (Machado Fernández, 2015b) se eligió utilizar 3000 muestras que se emplean para calcular la media y la varianza. Posteriormente, se aplican los dos bloques fundamentales de la arquitectura: la estimación del parámetro de forma del clutter Weibull y la transformación de este parámetro a una corrección viable del factor.
La estimación por el MoM utiliza las siguientes expresiones para la media y la varianza (O’Connor 2011):
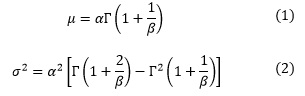
Y las combina para eliminar la influencia del parámetro de escala de la distribución:
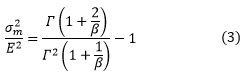
La expresión (3) debe resolverse numéricamente pues no es posible extraer la β de dentro de la función Gamma ![]() .
.
El lector debe notar que, como el parámetro de forma es el que tiene influencia en la detección (Machado Fernández and Bacallao Vidal, 2014), no es necesario calcular el parámetro de escala.
Para transformar el parámetro de forma a un valor del factor de ajuste CA-CFAR el diseñador debe seleccionar la probabilidad de falsa alarma a la cuál desea que opere el sistema. Las siguientes expresiones permiten obtener T a partir de β para ![]() respectivamente (Machado Fernández, 2015a):
respectivamente (Machado Fernández, 2015a):
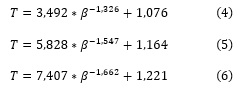
Implementación VHDL
La implementación en VHDL entrañó algunas complejidades debido a la naturaleza de bajo nivel del soporte. En primer lugar, fue necesario organizar la generación de muestras dentro del propio esquema con el objetivo de efectuar pruebas. Para ello se construyó un bloque que leía de una memoria ROM (Read Only Memory, Memoria de Solo Lectura) donde estaban almacenadas 20 000 muestras Weibull.
En segundo lugar, fue necesario normalizar las muestras para forzarlas a tener media igual a uno. El propio sistema realiza la labor dividiendo cada nueva muestra adquirida por la media. Esto se hizo para disminuir los tiempos de procesamiento y lograr que el sistema funcionara en tiempo real (se adquiere una nueva muestra cada 1µ). El problema radica en que una media cambiante obliga a recalcular la varianza de cada una de las 3000 muestras almacenadas. Con la media normalizada, el aporte de cada elemento al cálculo de la varianza es tenido en cuenta solo en el momento de la adquisición y se mantiene hasta que la muestra abandona el sistema.
Por último, los autores se enfrentaron al problema de implementar el cálculo del parámetro β en VHDL de acuerdo a (3). Para realizar la búsqueda binaria requerida, se precisaba de una forma de evaluar la función Gamma que está definida como una integral no reducible a una expresión cerrada (O’Connor, 2011). Como solución, se guardó en ROM una tabla de valores que permitían reemplazar el uso de la función Gamma. Fue elegida una resolución de 14 bits para cada valor almacenado, luego de comprobar en MATLAB que con ello se lograba que no se afectara la precisión de los resultados.
RESULTADOS Y DISCUSIÓN
Luego del comentario sobre los detalles de la implementación efectuado en la sección previa, el acápite actual se dedica a ofrecer evidencia del adecuado funcionamiento de la arquitectura.
Primeramente, para validar la implementación realizada en VHDL los autores reprodujeron el detector W-MoM-CA-CFAR en MATLAB, incluyendo las limitaciones y los comportamientos observados en la solución de circuito integrado. Entonces, comprobaron que la correspondencia entre ambas soluciones fuera exacta. La figura 3 muestra las respuestas ofrecidas por las dos variantes ante una entrada común. Tras procesar muestras de clutter, ambas cometen falsas alarmas en las mismas celdas, luego de pasado el período de inicio de los mecanismos que hace que la implementación VHDL incurra en una gran cantidad de errores.
El W-MoM-CA-CFAR de VHDL necesita al menos almacenar 3000 muestras para poder calcular la media y la varianza y realizar la estimación correspondiente del factor de ajuste. Por tanto, el tiempo inicial que corresponde al inicio de los mecanismos no aporta resultados válidos.
Con respecto al funcionamiento de la arquitectura, la figura 4 muestra el re-cálculo constante de la media una vez que el sistema ha alcanzado la estabilidad. Como puede apreciarse, el valor estimado oscila alrededor de la cifra teórica con que fueron generadas las muestras. El valor de β utilizado fue de 1,75.
Un comportamiento similar se observó en el cálculo de la varianza que se grafica en la figura 5. El error promedio en la estimación de la media luego de procesar 100 000 muestras Weibull fue de 0,0157 lo que representa un error relativo de 0,87%; mientras que el error promedio para la varianza fue de 0,0256 para un error relativo de 2,28%.
El error introducido en la estimación de la media y la varianza hace que al aplicarse el método de los momentos se obtenga una estimación inexacta del parámetro de forma del clutter Weibull. La figura 6 (izquierda) contiene el histograma de los valores estimados para β= 1.75 que obedece a una distribución aproximadamente Gaussiana. El error absoluto cometido fue de 0,0222 y el error porcentual de 1,271%.
A su vez, la desviación en la estimación de β genera inexactitudes en el subsecuente cálculo de T a partir de las ecuaciones (4), (5) y (6). En la figura 6 (derecha) se presenta un segundo histograma correspondiente a la estimación de T.
También con un comportamiento aproximadamente gaussiano, el histograma refleja la traducción del error en la estimación estadística hacia la operación del detector CA-CFAR. El factor de ajuste estimado tiene una diferencia promedio de 0,0397 con respecto al valor ideal (T=3,6161) que corresponde a β=1.75, lo que representa un error relativo de 1,0991%.
Obsérvese que los dos histogramas graficados son similares: la región anterior del primero es muy parecida a la cola del segundo; y la cola del primero guarda un alto grado de semejanza con la región anterior del primero. Este hecho se justifica en la relación inversa existente entre βy T que fue descrita en (Machado Fernández 2015a).
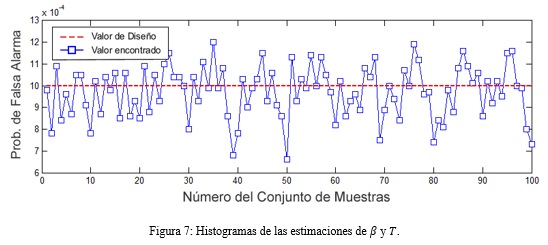
Finalmente, la figura 7 presenta la influencia del error en las estimaciones de la media y la varianza sobre el mantenimiento de la probabilidad de falsa alarma operacional del CA-CFAR. La figura 7 grafica 100 valores de Pf obtenidos luego de procesar 100 conjuntos de 10 000 muestras cada uno, cuyos parámetros de forma se hicieron cambiar continuamente.
Como se aprecia en la figura, la probabilidad operacional exhibe tanto desviaciones positivas como negativas con respecto a la de diseño (10-3). No obstante, puede observarse una ligera preponderancia de los errores por defecto que se justifican dada la cola alargada del histograma presentado en la figura 6 (derecha). Nótese que un error por exceso en el factor de ajuste provoca una Pf reducida.
Cuantificando los resultados, el error promedio en la desviación de la Pf fue de 12,7 * 10-5 que se corresponde con un 12,7% del valor que se desea establecer. Este valor está de acuerdo con la propuesta original ofrecida en (Machado Fernández 2015b) y verifica que la corrección introducida cumple su propósito de mantener la probabilidad de falsa alarma cercana al valor de diseño.
CONCLUSIONES Y TRABAJO FUTURO
Se implementó el detector W-MoM-CA-CFAR en VHDL utilizando 64 celdas de referencia, luego de resolver varias problemáticas vinculadas a dificultades intrínsecas del lenguaje. Validada por comparación con una variante similar creada en MATLAB, la solución permite la aplicación del esquema en ambientes prácticos, más allá de los laboratorios de pruebas. Se demostró además que la implementación sostiene un buen desempeño con una desviación reducida de la probabilidad de falsa alarma operacional aun cuando el clutter marino distribuido Weibull sufre cambios en su parámetro de forma. El artículo contribuye al desarrollo de una nueva variante CFAR que corrige un problema poco tratado en la literatura.
Los autores consideran que la investigación puede continuarse reproduciendo lo ofrecido para otras distribuciones de probabilidad relacionadas al clutter como la Log-Normal, la K y la Pareto. Recomiendan igualmente la concepción de un esquema que sea capaz de detectar los cambios bruscos de nivel en el clutter y realice las correcciones necesarias en el detector.
REFERENCIAS BIBLIOGRÁFICAS
CAI, L., X. MA, C. HAO AND X. YANG. Performace Analysis of Distributed Fuzzy CA-CFAR Detector in Pearson Distributed Clutter. Presentado en Proceedings of the Sixth International Conference on Fuzzy Systems and Knowledge, 491-495, 2009.
CASO, G. AND L. DE NARDIS 2013. Cooperative Spectrum Sensing based on Majority decision under CFAR and CDR constraints. Presentado en Proceedings of the Workshop on Cognitive Radio Medium Access Control and Network Solutions, IEEE 24th International Symposium on Personal, Indoor and Mobile Radio Communications, 51-55, 2013.
FARINA, A. AND F. A. STUDER. A Review of CFAR Detection Techniques in Radar Systems. Microwave Journal, 29(1), 115-118, 1986.
KOUEMOU, G. Radar Technology. Edtion ed.: I-Tech, 2009.
MACHADO FERNÁNDEZ, J. R. AND J. C. BACALLAO VIDAL MATE-CFAR: Ambiente de Pruebas para Detectores CFAR en MATLAB. Telem@tica, 13(3), 86-98, 2014.
MACHADO FERNÁNDEZ, J. R., J. C. BACALLAO VIDAL AND N. CHÁVEZ FERRY A Neural Network Approach to Weibull Distributed Sea Clutter Parameter's Estimation. Inteligencia Artificial, 18(56), 3-13, 2015.
MACHADO FERNÁNDEZ, J. R. AND R. C. SÁNCHEZ RAMS Implementación de un Detector de Promediación de Clutter (CA-CFAR) usando VHDL (aceptado). Telem@tica, 2016.
MADISETTI, V. K. The Digital Signal Processing Handbook. CRC Press, 2010.
SKOLNIK, M. I. Radar Handbook. McGraw-Hill, 2008.
Recibido: 02/09/2016
Aceptado: 02/06/2017