Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.12 no.3 La Habana jul.-set. 2018
ARTÍCULO ORIGINAL
Estructuración de la base de conocimiento en un Sistema Basado en Casos utilizando algoritmos conceptuales.
Structuring the knowledge base in a Case-Based System using conceptual algorithms.
Yunia Reyes González1*, Natalia Martínez Sánchez2, María Matilde García Lorenzo3
1Facultad 2. Universidad de las Ciencias Informáticas. yrglez@uci.cu
2Vicerrectoría de Formación. Universidad de las Ciencias Informáticas. natalia@uci.cu
3Universidad Central de Las Villas. mmgarcia@uclv.edu.cu
*Autor para la correspondencia: yrglez@uci.cu
RESUMEN
Los Sistemas Basados en Casos constituyen un paradigma de la Inteligencia Artificial ampliamente utilizado para la construcción de sistemas inteligentes de apoyo a la toma de decisiones. Sin embargo, persisten limitaciones relacionadas fundamentalmente con la organización de la base de conocimientos y el tratamiento de los valores numéricos y no numéricos que afectan la eficacia de las respuestas en este tipo de sistemas. En esta investigación se presenta una propuesta de procedimientos a seguir para estructurar jerárquicamente la base de conocimiento en un Sistema Basado en Casos utilizando los algoritmos conceptuales del Reconocimiento Lógico Combinatorio de Patrones que favorece el acceso y recuperación de los casos semejantes para dar solución a problemas caracterizados por datos mezclados e incompletos. El modelo se valida a partir de experimentos que utilizan la prueba de Friedman demostrándose los resultados significativamente superiores de la estructura jerárquica conceptual propuesta con relación a similares estructuras que conforman jerarquías.
Palabras clave: algoritmos conceptuales, sistemas basados en casos, reconocimiento lógico combinatorio de patrones.
ABSTRACT
Case-based Systems are an Artificial Intelligence paradigm widely used for the construction of intelligent decision support systems. However, there are still limitations related to the knowledge base organization and the treatment of numerical and non-numerical values that affect the effectiveness of the responses in this type of system. This research presents a proposal of procedures to be followed to hierarchically structure the knowledge base in a Case Based System using the conceptual algorithms of the Logical Combinatorial Pattern Recognition that favors the access and retrieve of similar cases to solve problems characterized for mixed and incomplete data. The model is validated from experiments that use the Friedman test demonstrating the significantly superior results of the proposed conceptual hierarchical structure in relation to similar structures that form hierarchies.
Key words: case-based systems, conceptual algorithms, logical combinatorial pattern recognition
INTRODUCCIÓN
Un Sistema Basado en Casos es un tipo de sistema basado en el conocimiento en el que la forma de representar el conocimiento son los casos y el método de solución de problemas es el Razonamiento Basado en Casos (RBC) (Kolodner 1992); (Aamodt y Plaza 1994); (Riesbeck y Schank 2013).
Autores tales como Richter y Weber (2013); Fan et al. (2014); Li et al. (2015) y Kang, Krishnaswamy y Zaslavsky (2014) coinciden en señalar la importancia de una eficiente recuperación de los casos semejantes para el funcionamiento de los sistemas basados en casos. En esto intervienen dos aspectos principales: la estructura de la base de casos y cómo se realiza la comparación entre las descripciones del caso y el problema a resolver.
La organización de la memoria define el acceso a los casos y de esta depende que la eficiencia en la recuperación no se afecte por el volumen de la experiencia almacenada. En la medida que se alcance una combinación efectiva de ambas componentes se determina el éxito o el fracaso del sistema.
Por tal motivo, en los últimos años, la investigación en este campo se dirige a la búsqueda de una estructura para la base de casos que garantice la eficiencia en la recuperación (Müller y Bergmann 2014); (Perner 2014); (Sarkheyli y Söffker 2015). Principalmente se desarrollan distintas técnicas que faciliten un acceso rápido a los casos relevantes de determinadas aplicaciones en grandes bases de casos. La literatura clásica revisada (Richter y Weber 2013); (Herrero et al. 2015); (Peula et al. 2017) distingue –principalmente- dos enfoques en esta dirección: la organización de los casos en una estructura plana y la organización siguiendo una estructura jerárquica. En la estructura plana los casos se disponen de manera secuencial por lo que se garantiza encontrar el más similar, pero presenta el inconveniente de la complejidad temporal cuando crece el volumen de datos (Peula et al. 2017). Por otra parte, la estructura jerárquica es una alternativa ante el problema de la complejidad temporal, sin embargo, no siempre garantiza encontrar el caso más similar (Herrero et al. 2015) y hace más complejo el aprendizaje incremental de casos solucionados.
La representación de los casos en jerarquías (Guo, Hu y Peng 2014); (Han y Cao 2015); (Fernandes et al. 2016) y (Cao et al. 2017) recibe la mayor atención por las posibilidades que ofrece para el posterior proceso de recuperación. Un método comúnmente utilizado con este propósito, aunque criticado por autores como (Jänichen y Perner 2005), consiste en fragmentar la base de casos aplicando algoritmos de agrupamiento jerárquicos aglomerativos (Aggarwal y Reddy 2013) o divisivos (Goyal y Srivastava 2016). Como alternativa en Perner (2006) se propone una estructuración jerárquica conceptual para la base de casos, donde los conceptos constituyen prototipos de subconjuntos de grafos que se determinan calculando el centroide del grupo (Fränti, Rezaei y Zhao 2014) o seleccionando el medoide (Aggarwal y Reddy 2013) como un caso natural representativo del agrupamiento. En estas variantes los prototipos, no siempre representan en su totalidad las características de los objetos de su agrupación.
Otros antecedentes importantes en el empleo del agrupamiento conceptual para la organización de la base de casos son los trabajos de Börner, Wode y Faßauer (1996); Dıaz-Agudo y González-Calero (2001) y Sun et al. (2014). El primero de ellos utiliza el algoritmo Galois y el análisis de conceptos formales (del inglés formal concept analysis) para construir un grafo de casos. Su principal inconveniente es que no puede aplicarse para casos descritos por atributos multi-evaluados y la necesidad de recalcular el grafo cuando se incorporan nuevos casos. El segundo y tercero construyen conceptos basados en probabilidades aplicando una técnica jerárquica aglomerativa similar a la propuesta por Perner (2006), pero estas dificultan la comprensión de las descripciones conceptuales y consecuentemente afectan el acceso a los casos semejantes, pues la comparación del nuevo problema con los prototipos conceptuales se realiza en función de medidas numéricas y no de las propiedades naturales basadas en los rasgos de los casos.
Por otro lado los autores Huang et al. (2012) y Rezvan, Zeinal Hamadani y Shalbafzadeh (2013) se refieren a la importancia que merece la selección del conjunto adecuado de rasgos. En esto influye la determinación de sus pesos, las funciones utilizadas para comparar los rasgos y los casos, así como el apropiado tratamiento en dependencia de sus valores. Cuando los casos están conformados por rasgos numéricos y no numéricos simultáneamente (mezclados) o con valores ausentes (incompletos), se requiere de un procesamiento adecuado para que la modelación sea lo más cercana posible a la realidad. Sin embargo, históricamente se emplean formas, a juicio de esta autora y de acuerdo con Ruiz-Shulcloper (2009), inapropiadas para lidiar con la anterior problemática tales como:
-
Codificar valores de los rasgos cualitativos como valores numéricos, y aplicar medidas de distancia usadas en casos numéricos.
-
Discretizar rasgos numéricos y aplicar algoritmos que manejen sólo información cualitativa.
-
Generalizar funciones de comparación diseñadas para rasgos cuantitativos para manejar rasgos cuantitativos y cualitativos.
Una primera solución a la anterior problemática la ofrece el Reconocimiento Lógico Combinatorio de Patrones (RLCP) Ruiz-Shulcloper (2013), que permite manipular datos mezclados e incompletos de manera simultánea.
Por otro lado, la mayoría de los métodos de agrupamiento propuestos en la literatura ofrecen estructuraciones de los espacios sobre los que se aplican en forma extensional, es decir, determinan qué objetos están en un cierto agrupamiento. Los algoritmos propuestos por Michalski (1979) se reconocen en la literatura como los primeros en brindar una estructuración conceptual o intencional del espacio, es decir, además de organizar los objetos en grupos, estos pretenden descubrir las características, propiedades o conceptos de estos agrupamientos.
Los algoritmos conceptuales, de manera general, siguen una de las tres aproximaciones siguientes: construyen primero la descripción extensional de los grupos y con base en esta, la descripción intencional (conceptos) de los grupos; determinan primero un conjunto de conceptos presentes en la colección y posteriormente, forman la descripción extensional de cada grupo considerando los objetos que más se ajustan a dichos conceptos o construyen a la misma vez la descripción extensional e intencional de los grupos (Suárez Pérez y Medina Pagola 2014).
Basados en los fundamentos del enfoque lógico combinatorio para problemas no supervisados, se distinguen algoritmos como el LC-Conceptual (Martínez-Trinidad y Sánchez-Díaz 2001) y el RGC (Pons Porrata 1999) que retoman las ideas propuestas por Michalski para generar conceptos, interpretables por los especialistas, en términos del conjunto de rasgos original. Las características distintivas de estos algoritmos constituyen factores a estudiar para la organización jerárquica de la base de casos en un Sistema Basado en Casos.
El propósito de esta investigación consiste en desarrollar una organización jerárquica de la base de casos utilizando algoritmos conceptuales del Reconocimiento Lógico Combinatorio de Patrones para favorecer el acceso y recuperación de los casos semejantes.
MATERIALES Y MÉTODOS
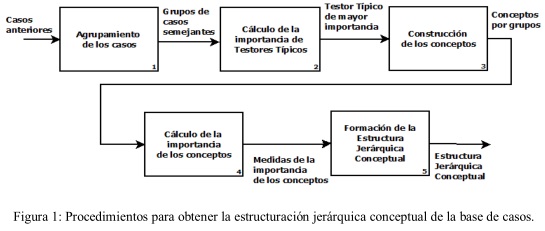
Para construir la estructura jerárquica conceptual de la base de casos se proponen cinco procedimientos que se corresponden con el agrupamiento de los casos, la selección de rasgos, la obtención de los conceptos, el cálculo de la importancia de los conceptos y la formación de la estructura jerárquica como se ilustra en la figura 1.
La base de casos responde a una estructura jerárquica conceptual, en la que se destacan en los niveles superiores de la jerarquía los conceptos que se corresponden con los agrupamientos. El nodo raíz contiene una abstracción de todos los La base de casos responde a una estructura jerárquica conceptual, en la que se destacan en los niveles superiores de la jerarquía los conceptos que se corresponden con los agrupamientos. El nodo raíz contiene una abstracción de todos los casos del sistema. En el segundo nivel se localizan los conceptos expresados mediante complejos lógicos (lcomplejos que constituyen formas normales disyuntivas).
Agrupamiento de los Casos
Datos de entrada:
-
Matriz inicial
-
Función de semejanza para comparar los casos
-
Funciones de comparación por rasgos
-
Criterio de agrupamiento
1: Construir la matriz de semejanza utilizando una función de semejanza.
2: Calcular el umbral de semejanza utilizando un criterio ![]()
3: Aplicar criterio de agrupamiento β0 - Conexo.
Datos de salida:
-
ME //Matriz estructurada en c agrupamientos (Kc).
La selección del criterio de agrupamiento se deja abierta según las características del dominio de aplicación y la valoración de los expertos, pudiendo decidirse entre aquel que calcula las componentes βo-Conexas o los conjuntos βo-Compactos (Ruiz-Shulcloper 2009). Se recomienda utilizar el criterio βo-Conexo y si es necesario volver a aplicar dentro de algún agrupamiento otro criterio entonces se sugiere el βo-Compacto, aunque esta elección depende del problema en particular.
Como dato de salida del algoritmo 1 se obtiene una estructuración de la base de casos, en c agrupamientos, con los cuales se conforma una matriz de entrenamiento (ME). En esta investigación se denomina grupos o clases indistintamente a los conjuntos de casos que se obtienen en el proceso de agrupamiento.
Selección de rasgos
Una vez que se obtienen los agrupamientos se utiliza la teoría de testores como herramienta matemática para la selección de rasgos. De este modo se reduce la cantidad de atributos con los cuales se deben describir los casos y se determinan los que inciden de manera determinante en el problema.
Datos de entrada:
-
ME// Matriz de Entrenamiento
-
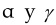 //Parámetros para ponderar la frecuencia y longitud
//Parámetros para ponderar la frecuencia y longitud
1: Calcular la matriz de diferencias.
2: Calcular la matriz básica.
3: Aplicar algoritmo Fast-BR (Lias-Rodríguez y Sánchez-Díaz 2013) para el cálculo de los testores típicos.
4: Calcular el peso εi de los rasgos xi que aparecen en la familia de testores típicos según:
![]()
5: Seleccionar los testores típicos de menor longitud.
6: Calcular el peso de los testores típicos de menor longitud según: 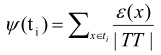
Seleccionar el testor típico de mayor peso informacional (t).
Datos de salida:
-
t //Testor típico de menor longitud y mayor peso informacional.
-
εi //Importancia de los rasgos que aparecen en los testores
Como el número de testores típicos puede ser alto, a cada agrupamiento se asocia una gran cantidad de conceptos o propiedades, por lo que en este modelo se propone seleccionar aquellos testores típicos de menor longitud, teniendo en cuenta que independientemente de esta, todos los testores típicos permiten distinguir objetos de clases diferentes.
Generación de los Conceptos
El cálculo de los conceptos para cada uno de los agrupamientos de la estructuración se realiza a partir del testor típico de mayor peso informacional. Se aplica el procedimiento del cálculo de la estrella que emplea el operador Refunión Condicionada (Martínez-Trinidad y Sánchez-Diaz 2001) para obtener los conceptos expresados en forma de complejos lógicos denominados l-complejos. En el cálculo de la estrella para cada l-complejo de cada clase Ki se generan todas las combinaciones posibles con los valores que toman los rasgos que los conforman y se seleccionan aquellos l-complejos que sólo representan a objetos de la clase Ki.
Datos de entrada:
-
ME //Matriz de entrenamiento
-
t // Testor típico de mayor peso informacional
1: Calcular la estrella G(Ki\ K1, ..., Ki-1, Ki+1, ..., Kc) para cada clase Ki, i = 1,…, c utilizando el operador de Refunión Condicionada (RUC).
2: Aplicar reglas de generalización en dependencia del tipo de variable.
Datos de salida:
-
l-complejos //Conceptos para cada agrupamiento
En esta investigación se asume que un concepto, denotado por P, es la expresión lógica compuesta por la disyunción de l-complejos que satisface a todos los objetos del agrupamiento para el que es construido y se calcula mediante la aplicación del operador RUC a partir del testor típico de mayor peso informacional. Estos conceptos cumplen las propiedades de ser: caracterizantes debido a que cubren a todos los objetos del agrupamiento que describen; excluyentes porque no son satisfechos por ningún objeto de otro agrupamiento y clasificadores pues es posible determinar a partir de ellos los objetos de la matriz inicial que lo satisfacen (Pons Porrata 1999).
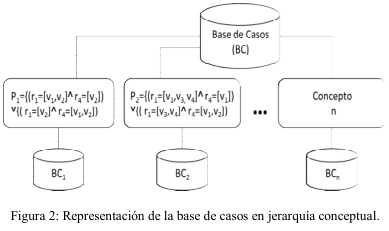
Además los conceptos generados cubren eventos observados y no observados (Michalski 1979). Los eventos observados son aquellos que representan objetos cuyas descripciones aparecen en el agrupamiento y los no observados son combinaciones de valores, generadas como resultado de aplicar el operador RUC, que se corresponden con objetos que no están físicamente en el grupo. La figura 2 ilustra un ejemplo de una base de casos estructurada en n grupos.
Para el acceso y recuperación de los casos semejantes la base de casos debe poseer una estructura que facilite este proceso. El acceso eficaz se garantiza a través de los conceptos representativos para cada agrupamiento y la recuperación de los casos semejantes se realiza a través de la búsqueda hacia el interior de estos. Por tanto, dentro de cada conjunto se implementa una estrategia que consiste en descomponer los complejos lógicos en lo que las autoras denominan subconceptos que pueden ser vistos como sub-descripciones obtenidas a partir de la descomposición de los conceptos en subconjuntos de todas las posibles combinaciones de valores de los diferentes rasgos que representan a los objetos del agrupamiento.
Hacia el interior de cada agrupamiento los subconceptos se organizan en forma de árbol para facilitar la recuperación de los casos semejantes. Teniendo en cuenta que la búsqueda en esta estructura se inicia realizando recorridos de izquierda a derecha, la manera de situar los subconceptos es otro aspecto a considerar.
Cálculo de la importancia de los conceptos
En esta investigación se propone utilizar un conjunto de medidas de la importancia informacional de los valores de los rasgos en los conceptos, como heurísticas de preferencias (Kolodner 2014) para la construcción de la estructura jerárquica. Para ello se retoman las ideas iniciales planteadas en Reyes, Martínez y García (2015) y extendidas en Reyes et al. (2016) como continuidad de la investigación. Las medidas propuestas se fundamentan en la frecuencia de aparición de los valores de los rasgos en conceptos y subconceptos.
a) Importancia informacional del valor del rasgo 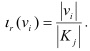 Se define como la relación que existe entre la
Se define como la relación que existe entre la
cantidad de objetos que presentan el valor vi en el rasgo ri y la cardinalidad de la clase. En la ecuación el subíndice i recorre la cantidad de valores del rasgo, r denota la cantidad de rasgos y j la cantidad de grupos formados. Esta medida determina una importancia para cada valor de los rasgos que aparecen en los testores típicos.
b) Representatividad de un subconcepto: 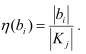 Se define como la relación que existe entre la cantidad de objetos representados por el subconcepto y la cardinalidad de la clase. En la ecuación el subíndice i recorre la cantidad de subconceptos de un agrupamiento y j la cantidad de grupos. El valor resultante indica cuán representativo es el subconcepto para la clase. Pueden realizarse diferentes análisis en torno a la representatividad de cada subconcepto en cada uno de los agrupamientos, sobre todo si estos son seleccionados en el proceso de recuperación de los casos semejantes.
Se define como la relación que existe entre la cantidad de objetos representados por el subconcepto y la cardinalidad de la clase. En la ecuación el subíndice i recorre la cantidad de subconceptos de un agrupamiento y j la cantidad de grupos. El valor resultante indica cuán representativo es el subconcepto para la clase. Pueden realizarse diferentes análisis en torno a la representatividad de cada subconcepto en cada uno de los agrupamientos, sobre todo si estos son seleccionados en el proceso de recuperación de los casos semejantes.
c) Representatividad de un concepto en la estructuración: ![]() Se define como la relación que existe entre la cardinalidad de cada clase (que coincide con la cantidad de objetos representados por el concepto) con respecto a la estructuración U. En la ecuación el subíndice j recorre la cantidad de clases y U representa el conjunto de objetos de la matriz inicial.
Se define como la relación que existe entre la cardinalidad de cada clase (que coincide con la cantidad de objetos representados por el concepto) con respecto a la estructuración U. En la ecuación el subíndice j recorre la cantidad de clases y U representa el conjunto de objetos de la matriz inicial.
A partir de la información que aportan las medidas es posible organizar los subconceptos de cada agrupamiento en un árbol jerárquico, donde los nodos son los rasgos que componen el testor típico y las ramas contienen los valores de estos. En las hojas del árbol se localizan los casos que comparten las características de cada rama.
Formación de la estructura jerárquica conceptual
-
Calcular
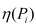 y
y 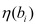 bi de todos los conceptos y subconceptos.
bi de todos los conceptos y subconceptos. -
Seleccionar el subconcepto de mayor
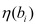 .
. -
Para cada rasgo del subconcepto de mayor
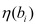 calcular
calcular 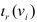 .
. -
Colocar como raíz del árbol el rasgo que contiene el valor de mayor
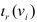 .
. -
Colocar en las ramas izquierdas subconceptos de mayor
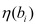 .
. -
Como rama derecha se sitúan los valores del rasgo que aparecen en el nodo padre en orden descendente de
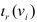 .
. -
El número de ramas está determinado por la cantidad de subconceptos.
-
Los nodos hojas contienen la cantidad de casos que se corresponden con las características de los subconceptos de cada rama.
RESULTADOS Y DISCUSIÓN
Para analizar los resultados de la estructura jerárquica propuesta, se utilizaron 15 conjuntos de datos de reconocimiento internacional disponibles en el repositorio para aprendizaje automatizado de la Universidad de Irvine, California (Merz y Murphy 1998). En la selección se consideran conjuntos de datos con variadas características como: la presencia de rasgos numéricos y no numéricos y la ausencia de información. La tabla 1 muestra un resumen de las bases de datos seleccionadas y su descripción.
De forma aleatoria, se obtiene el 75% de las instancias como conjuntos de entrenamiento y el 25% como prueba para cada base de datos. Se realizan 10 iteraciones de este proceso siguiendo el principio de validación cruzada (k-fold cross validation). El análisis que se presenta en (Demšar 2006) constituye el punto de referencia para la definición de los experimentos los cuales proponen realizar la prueba no paramétrica de Friedman, en particular en esta investigación se utiliza la prueba de Iman y Davenport según lo sugerido en García et al. (2010). Se seleccionan: el algoritmo para el cálculo del Ideal de la clase (AIC) (Ruiz-Shulcloper 2009), el algoritmo Holotipo (MartínezTrinidad y Sánchez-Díaz 2001) y el algoritmo K-means (Aggarwal y Reddy 2013).
El algoritmo AIC, calcula el ideal dentro del agrupamiento que es el objeto de mayor peso informacional mientras que el holotipo es el objeto que más se parece a todos en su grupo. Ambos responden a los postulados teóricos del Reconocimiento Lógico Combinatorio de Patrones que es el enfoque sobre el cual se sustenta esta investigación. Por su parte el algoritmo K-means permite conformar agrupamientos calculando el centroide como el objeto que minimiza la distancia hacia el resto de los objetos del grupo.
Para comprobar la eficacia del modelo de la base de casos propuesto, este debe compararse con una estructuración plana de la base de casos, pues estas resultan poco eficientes cuando la cantidad de casos es grande, pero muy eficaces en la búsqueda de la solución. Es por ello que en el experimento se incluye el algoritmo K-MSN (Sánchez-Díaz et al. 2013) o k vecino más similar, el cual al emplear funciones de similitud se corresponde con los presupuestos del Reconocimiento Lógico Combinatorio de Patrones. Adicionalmente se evalúa el comportamiento de otro enfoque representativo de las organizaciones jerárquicas conceptuales a través del algoritmo Cobweb (Fisher 1987) y para completar el análisis se incluyen los resultados respecto a algoritmos que forman árboles de decisión como C4.5 (Quinlan 2014).
El experimento con el objetivo de determinar si existen diferencias significativas entre el modelo presentado en esta investigación y otros modelos de organización de la base de casos que utilizan los algoritmos AIC, Holotipo, Kmeans, COBWEB, C4.5 y K-MSN.
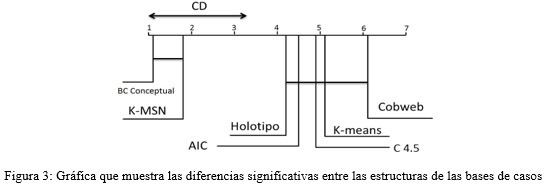
Se aplica la prueba de Friedman para la variable por ciento de clasificaciones correctas, con un intervalo de confianza de 95%. La hipótesis nula asume que todos los modelos son estadísticamente equivalentes. La prueba se realiza con un p-value < 2.2e-16, como este valor es inferior a 0.05 se rechaza la hipótesis nula y por tanto se puede afirmar que existen diferencias significativas entre los modelos comparados. Para detectarlas se aplica la prueba post hoc con la corrección de Finner, que arroja como resultados que la estructura jerárquica conceptual propuesta (señalada como BC Conceptual) supera en la comparación al resto de los modelos como se ilustra en la figura 3.
Como consecuencia inmediata se comprueba la validez de la estructura jerárquica conceptual de la base de conocimientos propuesta en esta investigación.
CONCLUSIONES
En este artículo se describe una estructura jerárquica conceptual para organizar la base de conocimiento en un sistema basado en casos que incorpora los sustentos teóricos de los algoritmos conceptuales en el marco del Reconocimiento Lógico Combinatorio de Patrones, posibilitando el adecuado tratamiento de los valores mezclados e incompletos y la selección de los rasgos relevantes a través de la teoría de testores.
Se propone una estructura jerárquica para la base de casos en la que los conceptos generados para los grupos constituyen expresiones lógicas de fácil interpretación las cuales representan en su totalidad las características de los casos en el agrupamiento y resulta más eficiente en la recuperación de casos semejantes con respecto a una estructura plana. Las medidas propuestas para calcular la importancia informacional de los conceptos constituyen heurísticas de gran importancia a tener en cuenta tanto para la organización jerárquica de cada agrupamiento como para la valoración de estos.
Los resultados experimentales demuestran que el modelo propuesto mejora la eficacia de las soluciones con respecto a modelos que utilizan organizaciones jerárquicas y planas para la base de casos. Se evidencian los resultados significativamente superiores de la estructura jerárquica conceptual propuesta con relación a similares estructuras que conforman jerarquías de conjuntos. El análisis en torno a la utilidad de los conceptos en la construcción de sistemas basados en casos, sugiere la posible extensión del modelo hacia la concepción de sistemas basados en reglas y el diseño de redes neuronales artificiales.
REFERENCIAS
AAMODT, A. y PLAZA, E., 1994. Case-Based Reasoning: Foundational Issues, Methodological Variations, and System Approaches. AI Communications, vol. 7, no. 1, pp. 39-59. ISSN 0921-7126. DOI 10.3233/AIC-19947104.
AGGARWAL, C.C. y REDDY, C.K., 2013. Data Clustering: Algorithms and Applications. S.l.: CRC Press. ISBN 978-1-4665-5821-2.
BÖRNER, K., WODE, H. y FAßAUER, R., 1996. Conceptual Analogy: Conceptual clustering for informed and efficient analogical reasoning. [en línea], [Consulta: 5 marzo 2017]. Disponible en: http://citeseerx.ist.psu.edu/viewdoc/citations;jsessionid=BD25936B25604BE9F2044AE3D86CE742?doi=10.1.1.44.8557.
CAO, M., ZHANG, S., YIN, Y. y SHAO, L., 2017. Classification and the case matching algorithm of the blast furnace burden surface. AIP Conference Proceedings. S.l.: AIP Publishing, pp. 080009. ISBN 0-7354-1488-2.
DEMŠAR, J., 2006. Statistical comparisons of classifiers over multiple data sets. Journal of Machine learning research, vol. 7, no. Jan, pp. 1-30. ISSN 1533-7928.
DÍAZ-AGUDO, B. y GONZÁLEZ-CALERO, P.A., 2001. Formal concept analysis as a support technique for CBR. Knowledge-Based Systems, vol. 14, no. 3–4, pp. 163-171. ISSN 0950-7051. DOI 10.1016/S09507051(01)00093-4.
FAN, Z.-P., LI, Y.-H., WANG, X. y LIU, Y., 2014. Hybrid similarity measure for case retrieval in CBR and its application to emergency response towards gas explosion. Expert Systems with Applications, vol. 41, no. 5, pp. 2526-2534. ISSN 0957-4174. DOI 10.1016/j.eswa.2013.09.051.
FERNANDES, F., ALVES, D., PINTO, T., TAKIGAWA, F., FERNANDES, R., MORAIS, H., VALE, Z. y KAGAN, N., 2016. Intelligent energy management using CBR: Brazilian residential consumption scenario. Computational Intelligence (SSCI), 2016 IEEE Symposium Series on. S.l.: IEEE, pp. 1-8. ISBN 1-5090-4240-7.
FISHER, D.H., 1987. Knowledge acquisition via incremental conceptual clustering. Machine Learning, vol. 2, no. 2, pp. 139-172. ISSN 1573-0565. DOI 10.1007/BF00114265.
FRÄNTI, P., REZAEI, M. y ZHAO, Q., 2014. Centroid index: cluster level similarity measure. Pattern Recognition, vol. 47, no. 9, pp. 3034-3045. ISSN 0031-3203.
GARCÍA, S., FERNÁNDEZ, A., LUENGO, J. y HERRERA, F., 2010. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Information Sciences, vol. 180, no. 10, pp. 2044-2064. ISSN 0020-0255.
GOYAL, R. y SRIVASTAVA, D.K., 2016. A Study on Cluster Analysis Technique-Hierarchical Algorithms. Imperial Journal of Interdisciplinary Research, vol. 2, no. 9. ISSN 2454-1362.
GUO, Y., HU, J. y PENG, Y., 2014. Research of new strategies for improving CBR system. Artificial Intelligence Review, vol. 42, no. 1, pp. 1-20. ISSN 0269-2821, 1573-7462. DOI 10.1007/s10462-012-9327-1.
HAN, M. y CAO, Z., 2015. An improved case-based reasoning method and its application in endpoint prediction of basic oxygen furnace. Neurocomputing, vol. 149, Part C, pp. 1245-1252. ISSN 0925-2312. DOI 10.1016/j.neucom.2014.09.003.
HERRERO, I., URDIALES, C., PEULA, J.M. y SANDOVAL, F., 2015. A bottom-up robot architecture based on learnt behaviors driven design. International Work-Conference on Artificial Neural Networks. S.l.: Springer, pp. 159-170. ISBN 978-3-319-19258-1. DOI 0.1007/978-3-319-19258-1 14.
HUANG, M.-L., HUNG, Y.-H., LEE, W.-M., LI, R.K. y WANG, T.-H., 2012. Usage of case-based reasoning, neural network and adaptive neuro-fuzzy inference system classification techniques in breast cancer dataset classification diagnosis. Journal of medical systems, vol. 36, no. 2, pp. 407-414. ISSN 0148-5598.
JÄNICHEN, S. y PERNER, P., 2005. Acquisition of Concept Descriptions by Conceptual Clustering. En: P. PERNER y A. IMIYA (eds.), Machine Learning and Data Mining in Pattern Recognition: 4th International Conference, MLDM 2005, Leipzig, Germany, July 9-11, 2005. Proceedings [en línea]. Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 153-162. ISBN 978-3-540-31891-0. Disponible en: http://dx.doi.org/10.1007/11510888_16.
KANG, Y.-B., KRISHNASWAMY, S. y ZASLAVSKY, A., 2014. A retrieval strategy for case-based reasoning using similarity and association knowledge. IEEE transactions on cybernetics, vol. 44, no. 4, pp. 473-487. ISSN 2168-2267.
KOLODNER, J., 2014. Selecting the best case for a case-based reasoner. P roceedings of. Michigan: s.n., pp. 155162. ISBN 0-8058-0684-9.
KOLODNER, J.L., 1992. An introduction to case-based reasoning. Artificial Intelligence Review, vol. 6, no. 1, pp. 334. ISSN 0269-2821, 1573-7462. DOI 10.1007/BF00155578.
LI, H., SONG, Y., LI, X., LIU, Q. y ZHU, Y., 2015. Research of CBR retrieval method based on rough set theory. Software Engineering and Service Science (ICSESS), 2015 6th IEEE International Conference on. S.l.: IEEE, pp. 990-993. ISBN 1-4799-8353-5.
LIAS-RODRÍGUEZ, A. y SÁNCHEZ-DÍAZ, G., 2013. An Algorithm for Computing Typical Testors Based on Elimination of Gaps and Reduction of columns. IJPRAI [en línea], vol. 27, no. 8. DOI 10.1142/S0218001413500225. Disponible en: http://dx.doi.org/10.1142/S0218001413500225.
MARTINEZ-TRINIDAD, J.F. y SÁNCHEZ-DIAZ, G., 2001. LC: A Conceptual Clustering Algorithm. En: P. PERNER (ed.), Machine Learning and Data Mining in Pattern Recognition: Second International Workshop, MLDM 2001 Leipzig, Germany, July 25–27, 2001 Proceedings [en línea]. Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 117-127. ISBN 978-3-540-44596-8. Disponible en: http://dx.doi.org/10.1007/3-540-44596X_10.
MERZ, C.J. y MURPHY, P.M., 1998. «UCI Repository of Machine Learning Databases» University of California at Irvine, Department of Information and Computer Science.
MICHALSKI, R.S., 1979. Conceptual Clustering: A Theoretical Foundation and a Method for Partitioning Data into Conjunctive Concepts. In Textes des exposes du Seminaire organise par l’Institute de Recherche d’Informatique et d’Automatique (IRIA). France: s.n., pp. 254-294.
MÜLLER, G. y BERGMANN, R., 2014. A Cluster-based Approach to Improve Similarity-based Retrieval for Process-oriented Case-based Reasoning. Proceedings of the Twenty-first European Conference on Artificial Intelligence [en línea]. Amsterdam, The Netherlands, The Netherlands: IOS Press, pp. 639–644. [Consulta: 4 marzo 2017]. ISBN 978-1-61499-418-3. DOI 10.3233/978-1-61499-419-0-639. Disponible en: https://doi.org/10.3233/978-1-61499-419-0-639.
PERNER, P., 2006. Case-base maintenance by conceptual clustering of graphs. Engineering Applications of Artificial Intelligence, vol. 19, no. 4, pp. 381-393. ISSN 09521976. DOI 10.1016/j.engappai.2006.01.014.
PERNER, P., 2014. Mining Sparse and Big Data by Case-based Reasoning. Procedia Computer Science, vol. 35, pp.
19-33. ISSN 1877-0509. DOI 10.1016/j.procs.2014.08.081.
PEULA, J.M., BALLESTEROS, J., URDIALES, C. y SANDOVAL, F., 2017. Biomimetic Navigation Using CBR. International Work-Conference on Artificial Neural Networks. S.l.: Springer, pp. 632-643.
PONS PORRATA, A., 1999. RGC: Un nuevo algoritmo de caracterización conceptual. Tesis para obtener el grado de Master en Ciencias de la Computación. S.l.: Universidad de Oriente.
QUINLAN, J.R., 2014. C4.5: Programs for Machine Learning. United States of America: Elsevier. ISBN 978-0-08050058-4.
REYES GONZALEZ, Y., MARTINEZ SANCHEZ, N. y GARCIA LORENZO, M.M., 2015. El agrupamiento conceptual en el contexto de la teoría de los conjuntos aproximados. DYNA New Technologies [en línea], vol. 2, no. 1. [Consulta: 27 marzo 2017]. Disponible en: http://www.dyna-newtech.com/busqueda-NT/elagrupamiento-conceptual-en-contexto-de-teoria-de-conjuntos-aproximados-2.
REYES GONZÁLEZ, Y., RODRÍGUEZ VALLEJO, L., MARTÍNEZ SÁNCHEZ, N. y YERO OSES, E.A., 2016. Métricas para la validación de los conceptos en el Reconocimiento Lógico Combinatorio de Patrones. XVI Convención y Feria Internacional INFORMÁTICA 2016 [en línea]. La Habana: s.n., Disponible en: http://www.informaticahabana.cu/sites/default/files/ponencias/CCI55.pdf.
REZVAN, M.T., ZEINAL HAMADANI, A. y SHALBAFZADEH, A., 2013. Case-based reasoning for classification in the mixed data sets employing the compound distance methods. Engineering Applications of Artificial Intelligence, vol. 26, no. 9, pp. 2001-2009. ISSN 0952-1976. DOI 10.1016/j.engappai.2013.07.014.
RICHTER, M.M. y WEBER, R., 2013. Case-Based Reasoning: A Textbook. S.l.: Springer Science & Business Media. ISBN 978-3-642-40167-1.
RIESBECK, C.K. y SCHANK, R.C., 2013. Inside Case-Based Reasoning. S.l.: Psychology Press. ISBN 978-1-13493002-9.
RUIZ-SHULCLOPER, J., 2009. Reconocimiento lógico combinatorio de patrones: teoría y aplicaciones. Tesis en opción al grado científico de Doctor en Ciencias. Santa Clara: Universidad Central de Las Villas.
RUIZ-SHULCLOPER, J., 2013. Acerca del surgimiento del Reconocimiento de Patrones en Cuba. Revista Cubana de Ciencias Informaticas, vol. 7, no. 2. ISSN ISSN 2227-1899.
SÁNCHEZ-DÍAZ, G., ESCOBAR-FRANCO, U.E., MORALES-MANILLA, L.R., PIZA-DÁVILA, I., AGUIRRESALADO, C. y FRANCO-ARCEGA, A., 2013. Un algoritmo de clasificación incremental basado en los k vecinos más similares para datos mezclados. Revista Facultad de Ingeniería Universidad de Antioquia, no. 67. ISSN 0120-6230.
SARKHEYLI, A. y SÖFFKER, D., 2015. Case indexing in Case-Based Reasoning by applying Situation Operator Model as knowledge representation model. IFAC-PapersOnLine, vol. 48, no. 1, pp. 81-86. ISSN 2405-8963. DOI 10.1016/j.ifacol.2015.05.048.
SUÁREZ PÉREZ, A. y MEDINA PAGOLA, J.E., 2014. Algoritmos para el agrupamiento conceptual de objetos. ISSN 2072-6260.
SUN, G., SAWARAGI, T., HORIGUCHI, Y. y NAKANISHI, H., 2014. Knowledge-Intensive Teaching Assistance System for Industrial Robots Using Case-Based Reasoning and Explanation-Based Learning. IFAC Proceedings Volumes, vol. 47, no. 3, pp. 4535-4540. ISSN 1474-6670.
Recibido: 06/12/2017
Aceptado: 25/04/2018