Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Informáticas
versión On-line ISSN 2227-1899
Rev cuba cienc informat vol.12 no.4 La Habana oct.-dic. 2018
ARTÍCULO ORIGINAL
Clasificación de interesados de proyectos basada en técnicas de soft computing
Project stakeholder classification based on soft computing techniques
Yasiel Pérez Vera1*, Anié Bermudez Peña2
1Universidad La Salle, Avenida Alfonso Ugarte 517, Cercado, Arequipa, Perú. yasielpv@gmail.com
2Universidad de las Ciencias Informáticas, Carretera San Antonio de los Baños, Km 2 ½, La Lisa, La Habana, Cuba. abp@uci.cu
*Autor para la correspondencia: yasielpv@gmail.com
RESUMEN
El proceso de clasificación de interesados es usualmente llevado a cabo por el director del proyecto utilizando métodos como la entrevista con expertos, la lluvia de ideas y listas de chequeo. Dichos métodos se llevan a cabo de forma manual y con carácter subjetivo por parte de especialistas vinculados a los proyectos. Esto afecta la exactitud de la clasificación y los directivos del proyecto no cuentan con una información más detallada a la hora de tomar decisiones sobre los involucrados. Como objetivo de este trabajo se propone un sistema borroso genético para la clasificación de interesados, que permita mejorar la calidad de la clasificación con respecto a la forma manual realizada en los proyectos. La propuesta realiza el aprendizaje automático y ajuste de sistemas de inferencia borrosos para la clasificación de interesados a partir de la ejecución de seis algoritmos genéticos: GFS.THRIFT, GFS.FR.MOGUL, GFS.GCCL, FH.GBML, GFS.LT.RS y SLAVE. Se examinan los resultados de aplicarlos en 10 iteraciones calculando las medidas: porciento de clasificaciones correctas, falsos positivos, falsos negativos, error cuadrático medio y error porcentual de la media absoluta simétrica. Los mejores resultados los obtiene el algoritmo FH.GBML. El sistema borroso genético desarrollado mejora la clasificación de los interesados mostrándose como una herramienta de apoyo a la toma de decisiones en organizaciones orientadas a la producción por proyectos.
Palabras clave: algoritmos genéticos, clasificación de interesados, gestión de proyectos, sistema de inferencia borroso, soft computing.
ABSTRACT
Stakeholder classification process is usually carried out by project manager using methods such as interviewing experts, brainstorming and checklists. These methods are carried out manually and subjectively by specialists belonging to the project. This affects the classification accuracy and project managers do not have more detailed information when making decisions about stakeholders. The objective of this research is to propose a genetic fuzzy system for classifying stakeholders for improving the classification quality with respect to the manually performed in projects. The proposal realizes the machine learning and adjustment of fuzzy inference systems for the stakeholder’s classification from the execution of six genetic algorithms: GFS.THRIFT, GFS.FR.MOGUL, GFS.GCCL, FH.GBML, GFS.LT.RS and SLAVE. It examines the results of applying them in 10 iterations by calculating the measures: accuracy, false positive, false negative, mean square error and symmetric mean absolute percentage error. The best results are shown by FH.GBML algorithm. The genetic fuzzy system implemented improves the stakeholder’s classification as a tool to support decision making in organizations oriented to production by projects.
Key words: fuzzy inference system, genetic algorithm, project management, soft computing, stakeholder classification.
INTRODUCCIÓN
El fracaso de un proyecto está fuertemente relacionado con la percepción que los interesados (stakeholders) tengan del valor del mismo y con el tipo de relaciones que se establezcan entre las partes involucradas. Los últimos resultados públicos en The CHAOS Report (The Standish Group, 2015) reflejan de forma clara que resulta significativo el número de proyectos de software que no culminan con éxito, solo el 29% son considerados como satisfactorios. En este estudio se analizan los factores que se consideran relevantes para lograr un proyecto exitoso y una gran parte está relacionada directamente con la gestión de los interesados (Pico López, 2016).
El término de stakeholder fue desarrollado por Edward Freeman en 1984, donde definió a los interesados como grupos o individuos que puedan afectar o se vean afectados por la consecución de los propósitos de la empresa (Freeman, 2010). Según el propio autor, estos grupos deben ser considerados como un elemento esencial en la planificación estratégica de la organización (Figuerola, 2013). El Instituto de Investigación de Stanford definió como actores interesados a aquellos grupos sin cuyo apoyo la organización dejaría de existir (Ortíz et al., 2016).
La gestión de los interesados en un proyecto incluye los procesos necesarios para identificarlos, analizar sus expectativas e impacto en el proyecto y desarrollar estrategias de gestión adecuadas a fin de lograr su participación eficaz en la toma de decisiones. La gestión de los interesados también se centra en la comunicación continua con los mismos para comprender sus necesidades y expectativas fomentando una adecuada participación en el proyecto. Una correcta identificación y clasificación de los involucrados, ayuda al director del proyecto a concentrarse en las relaciones necesarias para asegurar el éxito del proyecto (Schwalbe, 2015).
El proceso de clasificación de interesados es usualmente llevado a cabo por el director del proyecto utilizando técnicas como la entrevista con expertos, la lluvia de ideas y listas de chequeo (Project Management Institute, 2017). Existen varios métodos que hacen uso de diferentes atributos para caracterizar a los interesados. Dichos métodos se llevan a cabo de forma manual y con carácter subjetivo por parte de especialistas vinculados a los proyectos.
La valoración subjetiva de los especialistas del proyecto sobre la posesión de atributos por parte de los interesados suele ser de forma cualitativa. Así se introduce cierto grado de incertidumbre en el proceso de clasificación ya que cada experto tiene una apreciación diferente sobre el tema. Cuando no se tiene en cuenta este nivel de incertidumbre, ni se utilizan los métodos adecuados para su procesamiento, se produce pérdida de información que incide en la exactitud del resultado. Otra dificultad reside en la necesidad de contar con expertos que posean un amplio conocimiento del proyecto y sus involucrados.
Una alternativa de solución a los problemas antes mencionados, es la aplicación de aprendizaje automático. Este se muestra como un campo interdisciplinario donde intervienen: la estadística, la lógica, las matemáticas, las estructuras neuronales, la información teórica, la psicología, la biología, la inteligencia artificial y el soft computing (Ribas Moreno, 1994). Las técnicas de soft computing (computación blanda) aportan a las herramientas informáticas una aproximación al razonamiento humano, a través de la utilización del conocimiento y la experiencia acumulada (Bello y Verdegay, 2011). Dichas técnicas son robustas ante entornos con entradas ruidosas y tienen una alta tolerancia a la imprecisión de los datos con los que operan; permiten desarrollar soluciones de bajo costo y mayor capacidad de modelación.
Una de las técnicas que abarca el soft computing son los algoritmos genéticos (AG), estos están inspirados en la mecánica de selección natural y la genética humana. Los AG son lo suficientemente complejos para proporcionar mecanismos de búsqueda robustos, poderosos y han mostrado su eficiencia resolviendo problemas de optimización y clasificación (Villagra et al., 2006). Estas técnicas utilizan operadores aleatorios para explorar el espacio de soluciones en vez de operadores determinísticos, lo que hace que la convergencia de estas técnicas sea superior a las técnicas tradicionales.
Las insuficiencias en la clasificación manual de interesados afectan su exactitud y los directivos del proyecto no cuentan con información más detallada para tomar decisiones sobre los involucrados. Como objetivo de este trabajo se propone un sistema borroso genético para la clasificación de interesados, que permita mejorar la calidad de la clasificación respecto a la realizada por los directivos del proyecto de forma manual.
MATERIALES Y MÉTODOS
Como parte de la investigación, se realizó un estudio sobre el proceso de clasificación de interesados, así como la generación automática y optimización de reglas de inferencia borrosas, analizando los principales mecanismos para realizar los ajustes en los sistemas borrosos. A partir de dicho análisis se presentan los elementos fundamentales de los algoritmos genéticos aplicados en la generación del sistema borroso genético para la clasificación de interesados. Se presentan las bases del entorno de desarrollo utilizado para el aprendizaje, así como los parámetros de los algoritmos y el conjunto de datos de entrenamiento.
Clasificación de interesados
El proceso de clasificación de interesados tiene como objetivo agruparlos en función de sus características, funciones, expectativas, intereses e influencia en el proyecto. Una vez identificados y recopilada su información, los interesados son clasificados a fin de garantizar el uso eficiente del esfuerzo para comunicar y gestionar sus expectativas. Esto permite que el director de proyecto se concentre en las relaciones necesarias para asegurar el éxito del proyecto.
Existen varias técnicas para la clasificación de interesados entre las que se encuentra el modelo de prominencia de Mitchell (1997). Este modelo define la clasificación de interesados basado en un diagrama en el cual se relacionan las variables: poder, legitimidad y urgencia. La variable poder está dada por la capacidad del interesado de influenciar al proyecto; la variable legitimidad se refiere a la relación y a las acciones del interesado con el proyecto en términos de deseabilidad, propiedad o conveniencia; y la urgencia remite a la atención inmediata de los requisitos que los mismos plantean al proyecto. Según varias investigaciones (Poplawska, 2015; Samboni, 2015; Arévalo, 2013), este modelo es uno de los más discutidos y usados en el mundo. Por cada uno de estos atributos descritos, los expertos valoran el grado de posesión de los interesados. Esta clasificación dada por expertos contiene imprecisiones y vaguedad; problema que se persiguen solventar en esta investigación con la aplicación de sistemas de inferencia borrosos y técnicas de algoritmos genéticos, descritas a continuación.
Sistema borroso genético basado en la técnica de Thrift (GFS.THRIFT)
En (Thrift, 1991) se propone una técnica para generar reglas y optimizar sistemas de inferencia borrosos, basada en un algoritmo genético básico. GFS.THRIFT considera el sistema borroso tipo Mamdani (Mamdani, 1976) donde son representados los conjuntos borrosos en forma de tabla como genotipo con alelos. El fenotipo es producido por la fusificación, composición máxima y la defusificación. Los valores de los genes se representan como {Bien, Regular, Mal, _}; donde el símbolo _ indica que no hay entrada en dicha posición. Un cromosoma (genotipo) es formado por una tabla de decisión dirigida por filas que produce una cadena de números para los conjuntos codificados.
Para la selección se aplica una estrategia elitista por lo cual la mejor solución de una generación es promovida directamente a la siguiente generación del algoritmo genético. Un modelo con alto grado de elitismo consiste en utilizar una población intermedia con todos los padres (N) y todos los descendientes y seleccionar los N mejores. El operador de cruzamiento que se utiliza es el estándar de un punto de cruce. El operador de mutación cambia un código borroso cualquiera a su nivel superior o inferior, o al código vacío "_". Si el código actual es "_", se cambia a un código no vació seleccionado de forma aleatoria. La probabilidad de mutación y de cruzamiento son prefijadas.
Se realiza una cantidad de iteraciones definidas inicialmente para una población de soluciones generada mediante traslaciones a partir de la tabla de decisión. Cada cromosoma se evalúa según la función definida en dependencia del problema a resolver. El operador de defusificación aplicado es una simplificación del centroide: calcula el promedio pesado de los puntos centrales en los conjuntos borrosos de la variable de salida.
Sistema borroso genético basado en el aprendizaje iterativo de reglas (GFS.FR.MOGUL)
La técnica GFS.FR.MOGUL se basa en una metodología que utiliza el enfoque iterativo para el aprendizaje de reglas (Cordón et al., 1999). Este enfoque trata de resolver el problema del aprendizaje en tres etapas: generación de reglas lingüísticas, la multi-simplificación de las reglas generadas y el ajuste de las funciones de pertenencia de las reglas lingüísticas. De forma general, la primera etapa (generación) se dedica a fomentar la competición entre reglas individuales mientras que la segunda y tercera etapa (post-procesamiento) se enfocan en fomentar una buena cooperación entre las reglas generadas. Esto permite obtener una base de reglas borrosas con buen comportamiento global. A continuación, se refieren las tres etapas que componen el proceso de aprendizaje.
La primera consiste en un proceso iterativo de generación de reglas lingüísticas a partir de ejemplos, formado por dos componentes: un método de generación de reglas borrosas basado en un algoritmo inductivo no evolutivo y un método iterativo de cubrimiento del conjunto de ejemplos. La segunda etapa realiza un proceso genético de multi-simplificación para llevar a cabo la selección de reglas. Este proceso se implementa por medio de un algoritmo genético con codificación binaria que emplea una función de compartición genotípica y una medida del rendimiento del sistema basado en reglas borrosas. La tercera etapa ejecuta un proceso de ajuste basado en un algoritmo genético con codificación real y función de adaptación que considera dos criterios: una medida del rendimiento del sistema basado en reglas borrosas codificado en el cromosoma y una función que penaliza la no satisfacción de la propiedad de completitud. Este último proceso proporciona la base de reglas borrosas aprendidas ajustando las funciones de pertenencia que especifican la semántica de los términos lingüísticos existentes.
Sistema borroso genético basado en el aprendizaje cooperativo-competitivo (GFS.GCCL)
En (Ishibuchi, Nakashima y Murata, 1999) se propone un sistema de clasificación genético basado en un método heurístico de generación de reglas. Además, utiliza los operadores genéticos de selección, cruzamiento y mutación para generar combinaciones de conjuntos borrosos para los antecedentes de cada regla generada. Primeramente, se genera la población inicial de reglas borrosas de forma aleatoria a partir de los términos lingüísticos predeterminados y el grado de pertenencia de los consecuentes de las reglas es determinado por el método heurístico. Luego se evalúa cada regla generada de la población contando por cada regla la cantidad de casos clasificados correctamente.
El algoritmo continúa seleccionando dos reglas de la población actual de forma aleatoria, realiza el cruzamiento de sus antecedentes de forma uniforme y la mutación en dependencia de las probabilidades definidas para estas operaciones. Luego ocurre el remplazo de las peores reglas evaluadas de la población actual por las generadas anteriormente con los operadores genéticos. Si se cumple la condición de parada se tiene como resultado la población actual de reglas, sino se regresa a evaluar todas las reglas de la población. Usualmente se toma como condición de parada la cantidad de generaciones obtenidas lo que provee como resultado el mejor conjunto de reglas con el mayor porciento de clasificaciones correctas.
Sistema borroso genético híbrido de aprendizaje cooperativo-competitivo y enfoque Pittsburgh (FH.GBML)
En (Ishibuchi, Yamamoto y Nakashima, 2005) se presenta un algoritmo genético híbrido para el aprendizaje automático. Esta técnica combina el enfoque de Michigan (Booker, Goldberg y Holland, 1989) o de aprendizaje cooperativo-competitivo y el enfoque de Pittsburgh (Smith, 1980) para el diseño de un sistema genético borroso basado en reglas utilizado en problemas de clasificación. Este algoritmo híbrido es básicamente el enfoque de Pittsburgh, donde cada conjunto de reglas se maneja individualmente. El enfoque de Michigan, que tiene una alta capacidad de búsqueda para encontrar eficientemente buenas reglas borrosas, se utiliza como una especie de mutación heurística para modificar parcialmente cada conjunto de reglas.
Primeramente, se genera la población donde cada individuo de la población es un conjunto de reglas difusas. Como segundo paso se calcula el valor de la función objetivo de cada regla establecida en la población actual. Luego se deben generar los nuevos conjuntos de reglas mediante los operadores de selección, cruzamiento y mutación de la manera que lo hacen los algoritmos basados en el enfoque Pittsburgh. A continuación, se aplica una iteración del aprendizaje cooperativo-competitivo a cada uno de los conjuntos de reglas generados con una probabilidad definida por el sistema. Se adiciona el mejor conjunto de reglas de la población actual a los conjuntos de reglas recién generados para formar la siguiente población. Si no se cumple la condición de parada definida se vuelve al paso dos.
En este algoritmo híbrido, el enfoque de Michigan se utiliza para generar las reglas difusas debido a su alta capacidad de búsqueda. Por otro lado, el enfoque de Pittsburgh se utiliza para mejorar las combinaciones de reglas difusas generadas ya que posee una alta capacidad de optimización directa. De esta manera, FH.GBML aprovecha las ventajas de ambos enfoques. Este AG se puede extender al diseño multiobjetivo de sistemas borrosos basados en reglas buscando el equilibrio entre la exactitud de dichos sistemas y su complejidad.
Sistema borroso genético de ajuste lateral y selección de reglas (GFS.LT.RS)
En (Alcalá, Alcalá-Fdez y Herrera, 2007) se propone un mecanismo para realizar el ajuste lateral evolutivo de las funciones de pertenencia con el objetivo de obtener modelos lingüísticos con mayores niveles de precisión. Se presenta la cooperación del ajuste lateral junto con un mecanismo de selección de reglas borrosas, lo que reduce el espacio de búsqueda y facilita la legibilidad del sistema. Utiliza un esquema de representación de reglas basado en 2-tupla lingüística (Herrera y Martínez, 2000) que permite el desplazamiento lateral de las etiquetas de la función de pertenencia original. Las particiones borrosas se representan con funciones de pertenencia de tipo triángulo simétrico.
El esquema de codificación considera parámetros reales en los genes. En un cromosoma están contenidos todos los parámetros modificables y la estructura de la base de reglas. Para ambos modos de ajuste, la codificación de los genes es con números reales. Cada gen está asociado con el desplazamiento lateral de la correspondiente etiqueta en la base de reglas. Para obtener la población inicial se toma el primer individuo con todos sus parámetros de traslación en 0 y para el resto de los individuos se generan de forma aleatoria en el intervalo [-0.5, 0.5).
Este AG utiliza un enfoque de reinicio para escapar de los óptimos locales. En este caso, el mejor cromosoma se mantiene y los restantes se generan al azar dentro de los intervalos de variación correspondientes [-0.5, 0.5). Este procedimiento de reinicio se realiza cuando se alcanza un umbral o todos los individuos que conviven en la población son muy similares. Para mejorar la convergencia del algoritmo en problemas que deben ser resueltos con pocas evaluaciones, proponen no considerar el operador de mutación.
Sistema borroso genético basado en el algoritmo de aprendizaje estructural en ambientes de vaguedad (SLAVE)
En (González y Pérez, 1999) se presenta un algoritmo de aprendizaje inductivo que utiliza AG y los conceptos de lógica borrosa. SLAVE es capaz de aprender la estructura de la regla y hacer frente a la información con incertidumbre encontrando las variables predictivas que se necesitan para representar un valor concreto de la variable consecuente. En este algoritmo las variables generalmente son lingüísticas, es decir, los dominios de la variable se pueden describir usando etiquetas lingüísticas o conjuntos difusos generales. La clave de este modelo de reglas se basa en que cada variable puede tomar como valor un elemento o un subconjunto de un elemento de su dominio interpretándose como una disyunción de elementos.
SLAVE se basa en el método de aprendizaje de reglas iterativas, lo que significa que sólo obtiene una regla borrosa en cada ejecución del algoritmo genético. Con el fin de eliminar las variables irrelevantes en una regla, SLAVE tiene una estructura compuesta de dos pasos: representar la relevancia de las variables y definir los valores de los parámetros. Este método utiliza códigos binarios como representación de la población y aplica los operadores genéticos básicos, es decir, la selección, el cruce y la mutación.
En el proceso de aprendizaje de SLAVE, encontrar la mejor regla consiste en determinar la mejor combinación de valores de las variables antecedentes, dado un valor fijo para la variable consecuente y un conjunto de ejemplos. La mejor regla será la que cubra el número máximo de ejemplos de una clase (condición de completitud) y que no cubra ejemplos pertenecientes a distintas clases (condición de consistencia). Para determinar cuándo un conjunto de reglas es lo suficientemente representativa para un sistema, SLAVE comprueba que todos los ejemplos de la clase están adecuadamente cubiertos por las reglas obtenidas o el algoritmo de aprendizaje no es capaz de obtener una nueva regla útil.
Entorno de trabajo, parámetros utilizados en los algoritmos y datos de entrenamiento
Para la aplicación de los algoritmos se utiliza el lenguaje R y el entorno de PostgreSQL, que facilitan la incorporación de paquetes del R-Cran para su explotación y prueba en proyectos experimentales. Entre estos paquetes se encuentra FRBS: Fuzzy Rule-based Systems for Classification and Regression Tasks (sistemas basados en reglas borrosas para la clasificación y regresión de tareas) (Riza et al., 2015). FRBS se basa en el concepto de lógica borrosa propuesto por (Zadeh, 1994) y representa los sistemas borrosos para manejar diversos problemas mediante la implementación de técnicas de soft computing. Se hace uso de la funcionalidad frbs.learn del paquete FRBS con los parámetros de aprendizaje mostrados en la Tabla 1.
La construcción del sistema se realiza a partir de un conjunto de casos de entrenamiento correspondiente a 137 interesados pre clasificados por expertos. El proceso de entrenamiento consiste en suministrarle al sistema el conjunto de casos de interesados que le permite crear la base de conocimientos. En esta tarea se utilizan los datos de los interesados de los proyectos de la Dirección de Informatización de los que se contaba con su clasificación emitida por los expertos. Del total de interesados se utiliza el 80% para el entrenamiento y el resto para la validación del mismo.
RESULTADOS Y DISCUSIÓN
Se aplicó el sistema propuesto para la clasificación de interesados en los proyectos de la Dirección de Informatización de la Universidad de las Ciencias Informáticas. Los resultados obtenidos con la ejecución del sistema en las 10 combinaciones de datos permiten comparar el desempeño del sistema generado respecto a los distintos algoritmos genéticos utilizados. Se tienen en cuenta las siguientes métricas para validar el entrenamiento del sistema genético difuso: porciento de clasificaciones correctas, cantidad de falsos negativos, cantidad de falsos positivos, error cuadrático medio, raíz del error cuadrático medio, error porcentual de la media absoluta simétrica. A continuación, se analizan los resultados de cada una de estas métricas en la validación del entrenamiento.
El porciento de clasificaciones correctas (%CC) es el índice que especifica la cantidad porcentual de interesados clasificados correctamente. En la Figura 1 se muestra una comparación entre todos los algoritmos genéticos implementados respecto al porciento de clasificaciones correctas.
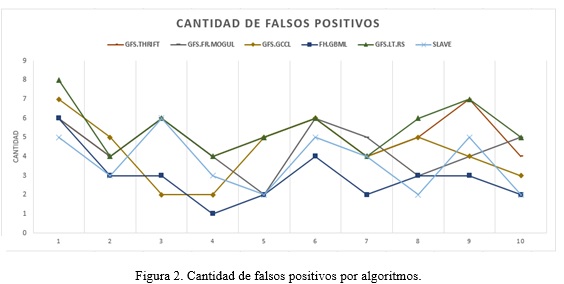
La cantidad de falsos positivos (CFP) es el índice que indica la cantidad de interesados clasificados en una categoría superior a la categoría que en realidad pertenecen. Este índice se refiere a cuántos interesados tienen menos prioridad que la que le determinó el sistema. En la Figura 2 se muestra una comparación entre todos los algoritmos genéticos implementados respecto a la cantidad de falsos positivos.
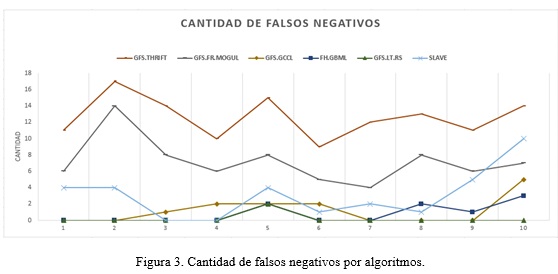
La cantidad de falsos negativos (CFN) es el índice que se refiere la cantidad de interesados clasificados en una categoría inferior a la categoría que en realidad pertenecen. Este índice indica cuántos interesados tienen más prioridad que la que le determinó el sistema. En la Figura 3 se muestra una comparación entre todos los algoritmos genéticos implementados respecto a la cantidad de falsos negativos.
El error cuadrático medio (MSE por sus siglas en inglés) es la medida de dispersión que calcula la diferencia entre cada clasificación y el promedio general. En la Figura 4 se muestra una comparación entre todos los algoritmos genéticos implementados respecto al error cuadrático medio.
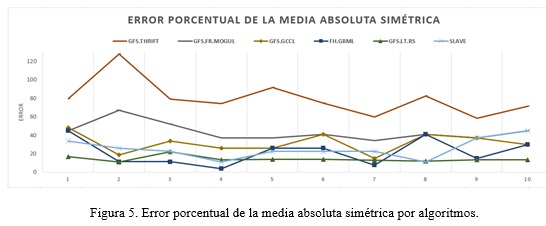
El error porcentual de la media absoluta simétrica (SMAPE por sus siglas en inglés) es la medida de dispersión que calcula el tamaño del error de clasificación en términos porcentuales. En la Figura 5 se muestra una comparación entre todos los algoritmos genéticos implementados respecto al error porcentual de la media absoluta simétrica.
Se comprueba que los datos de las métricas para la validación del entrenamiento, analizados anteriormente, no siguen una distribución normal al aplicar la prueba de Shapiro-Wilk para comprobar la normalidad de datos con menos de 2000 muestras. Teniendo esto en cuenta se aplica la prueba no paramétrica de Friedman para K muestras relacionadas, para cada uno de los índices analizados. Los resultados mostraron que existen diferencias significativas entre las técnicas por lo que se aplica la prueba de Wilcoxon. Para ambas pruebas (Friedman y Wilcoxon) se aplicó el método de simulación Monte Carlo con un 99% de intervalo de confianza.
El objetivo de aplicar la prueba de Wilcoxon es agrupar las técnicas que no tengan diferencias significativas en un mismo grupo. La Tabla 2 muestra el resultado de esta prueba no paramétrica donde se agrupan de forma ascendente los algoritmos, presentando los mejores de cada métrica en el “Grupo 1”.
Como se puede apreciar en todas las métricas, el sistema genético híbrido de aprendizaje cooperativo-competitivo y enfoque Pittsburgh (FH.GBML) presenta mejores resultados que el resto de los algoritmos genéticos aplicados. Estos resultados concuerdan con lo expresado en (Rodríguez y Verdecia, 2015) donde se analizan varias técnicas para el aprendizaje de reglas borrosas orientado a la evaluación de proyectos.
En este trabajo se realiza una comparación de seis técnicas con diferentes enfoques como son los algoritmos genéticos y los basados en particiones del espacio de búsqueda. Entre todos los algoritmos analizados en esta investigación, el algoritmo FH.GBML obtuvo mejores resultados que el resto. Esto sugiere que el sistema genético híbrido de aprendizaje cooperativo-competitivo y enfoque Pittsburgh es una buena estrategia a implementar en problemas de clasificación que utilicen un sistema basado en reglas borrosas.
CONCLUSIONES
En la presente investigación se propuso un sistema borroso genético para la clasificación de interesados, que permite mejorar la calidad de la clasificación respecto a la realizada por los directivos del proyecto de forma manual. La aplicación del sistema permite arribar a las siguientes conclusiones:
-
La aplicación de técnicas de soft computing en herramientas informáticas para la clasificación de interesados es una tendencia novedosa, permitiendo mejorar los sistemas informáticos de apoyo a la toma de decisiones en los proyectos.
-
El empleo de algoritmos genéticos para la clasificación de interesados de proyectos provee una manera adecuada de tratamiento de la incertidumbre en la información proporcionada en el proceso de clasificación de interesados.
-
El sistema genético híbrido de aprendizaje cooperativo-competitivo y enfoque Pittsburgh brinda mejores resultados para la clasificación de interesados que el resto de los algoritmos genéticos aplicados. Este sistema provee un porciento de clasificaciones correctas promedio mayor al 90%, valor que está por encima del resto de los algoritmos implementados.
- La utilización de un sistema borroso genético para la clasificación de interesados mejora el proceso de clasificación de los involucrados del proyecto debido a que el sistema propuesto maneja la incertidumbre de la información introducida en este proceso.
REFERENCIAS BIBLIOGRÁFICAS
ALCALÁ, R., ALCALÁ-FDEZ, J. y HERRERA, F., 2007. A proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection. IEEE Transactions on Fuzzy Systems, vol. 15, no. 4, pp. 616-635.
ARÉVALO, A.U., REQUENA, R., 2013. Considerations of the stakeholder approach. Punto de Vista, vol. 4, no. 7, pp. 31-50.
BELLO, R. y VERDEGAY, J.L., 2011. Los conjuntos aproximados en el contexto de la Soft Computing. Revista Cubana de Ciencias Informáticas [en línea], vol. 4, no. 1-2. ISSN 1994-1536.
BOOKER, L.B., GOLDBERG, D.E. y HOLLAND, J.H., 1989. Classifier systems and genetic algorithms. Artificial intelligence, vol. 40, no. 1-3, pp. 235-282.
CORDÓN, O., DEL JESÚS, M.J., HERRERA, F. y LOZANO, M., 1999. MOGUL: a methodology to obtain genetic fuzzy rule-based systems under the iterative rule learning approach. International Journal of Intelligent Systems, vol. 14, no. 11, pp. 1123-1153.
ELSAID, A., SALEM R. and ABDUL-KADER H., 2017. A Dynamic Stakeholder Classification and Prioritization Based on Hybrid Rough-fuzzy Method. Journal of Software Engineering, 11: 143-159.
FIGUEROLA, N., 2013. Procesos y Técnicas en la Gestión de los Interesados. PMQuality Artículos – Project Management [en línea]. Disponible en: https://articulospm.files.wordpress.com/2013/09/procesos-y-tc3a9cnicas-en-la-gestic3b3n-de-los-interesados.pdf.
FREEMAN, R.E., 2010. Strategic management: A stakeholder approach. S.l.: Cambridge University Press. ISBN 0-521-15174-0.
GONZÁLEZ, A. y PÉREZ, R., 1999. SLAVE: A genetic learning system based on an iterative approach. IEEE Transactions on Fuzzy Systems, vol. 7, no. 2, pp. 176-191.
HERRERA, F. y MARTÍNEZ, L., 2000. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Transactions on Fuzzy Systems, vol. 8, no. 6, pp. 746-752. ISSN 1063-6706. DOI 10.1109/91.890332.
ISHIBUCHI, H., NAKASHIMA, T. y MURATA, T., 1999. Performance evaluation of fuzzy classifier systems for multidimensional pattern classification problems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 29, no. 5, pp. 601-618.
ISHIBUCHI, H., YAMAMOTO, T. y NAKASHIMA, T., 2005. Hybridization of fuzzy GBML approaches for pattern classification problems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 35, no. 2, pp. 359-365.
MAMDANI, E.H., 1976. Application of fuzzy logic to approximate reasoning using linguistic synthesis. Proceedings of the sixth international symposium on Multiple-valued logic. S.l.: IEEE Computer Society Press, pp. 196-202.
MITCHELL, R.K., Agle, B.R., Wood, D.J.: Toward a Theory of Stakeholder Identification and Salience: Defining the Principle of Who and What Really Counts. The Academy of Management Review, vol. 22, no. 4, pp. 853 (1997). DOI: https://doi.org/10.5465/AMR.1997.9711022105
ORTÍZ, Y.V., MARTÍNEZ, E.E.V., ROGEL, R.M.N. y NECHAR, M.C., 2016. Los stakeholders de la industria hotelera: una clasificación a partir de sus intereses ambientales. Universidad & Empresa [en línea], vol. 18, no. 30, pp. 97-120. [Consulta: 21 junio 2016]. ISSN 2145-4558. Disponible en: http://revistas.urosario.edu.co/index.php/empresa/article/view/4607.
PICO LÓPEZ, Ó., 2016. Los Stakeholders como actores estratégico-instrumentales en los proyectos de la Nueva Gestión Pública [en línea]. Tesis de Máster. S.l.: Universidad de Oviedo. [Consulta: 13 diciembre 2016]. Disponible en: http://digibuo.uniovi.es/dspace/handle/10651/38421.
POPLAWSKA, J., LABIB, A., REED, D.M., ISHIZAKA, A., 2015. Stakeholder profile definition and salience measurement with fuzzy logic and visual analytics applied to corporate social responsibility case study. Journal of Cleaner Production, vol. 105, pp. 103-115. DOI: https://doi.org/10.1016/j.jclepro.2014.10.095
PROJECT MANAGEMENT INSTITUTE, 2017. A Guide to the Project Management Body of Knowledge. 6th Edition. Pennsylvania: Project Management Institute.
RIBAS MORENO, A., 1994. Aprendizaje automático. Universidad Politécnica de Cataluña. ISBN 84-7653-460-4.
RIZA, L.S., BERGMEIR, C., HERRERA, F. y BENÍTEZ SÁNCHEZ, J.M., 2015. FRBS: Fuzzy Rule-Based Systems for Classification and Regression in R. ISSN 1548-7660. DOI 10.18637/jss.v065.i06.
RODRÍGUEZ, C.R. y VERDECIA, P., 2015. Técnicas para el aprendizaje de reglas difusas para la toma de decisiones en gestión de proyectos. Tesis de Máster. La Habana, Cuba: Universidad de las Ciencias Informáticas.
SAMBONI, A.P., BLANCO, J.G., 2015. Herramientas de gestión de interesados utilizadas en las etapas de planeación y control de proyectos. Tesis, Universidad de San Buenaventura, Santiago de Cali. Available in: http://bibliotecadigital.usb.edu.co/bitstream/10819/2549/1/Herramientas_Interesados_Gestion_Etapas_Control_Proyectos_Samboni_2015.pdf
SCHWALBE, K., 2015. Information Technology Project Management. Cengage Learning. ISBN 978-1-305-17778-9.
SMITH, S.F., 1980. A learning system based on genetic adaptive algorithms. Ph. D. Thesis. University of Pittsburgh.
THE STANDISH GROUP, 2015. Standish Group 2015 Chaos Report - Q&A with Jennifer Lynch. InfoQ [en línea]. [Consulta: 13 diciembre 2016]. Disponible en: https://www.infoq.com/articles/standish-chaos-2015.
THRIFT, P.R., 1991. Fuzzy Logic Synthesis with Genetic Algorithms. ICGA. S.l.: s.n., pp. 509-513.
VILLAGRA, A., PANDOLFI, D., LASSO, M.G., SAN PEDRO, M.E. de y LEGUIZAMÓN, G., 2006. Algoritmos evolutivos y su aplicabilidad en la tarea de clasificación. VIII Workshop de Investigadores en Ciencias de la Computación. ISBN 978-950-9474-35-2. Disponible en: http://hdl.handle.net/10915/20711.
ZADEH, L.A., 1994. Fuzzy logic, neural networks, and soft computing. Communications of the ACM, vol. 37, no. 3, pp. 77-85.
Recibido: 17/12/2017
Aceptado: 19/10/2018