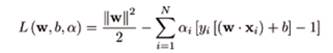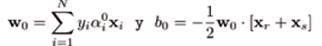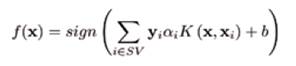INTRODUCCIÓN
Las herramientas de pronóstico son una necesidad ante los contextos cada vez más cambiantes y competitivos a los que se enfrentan las organizaciones; en ello existe un gran potencial para gestionar los riesgos inducidos por la incertidumbre en los escenarios en los que se convive. Como consecuencia, una aspiración real de muchas empresas es mejorar el proceso de toma de decisión basado en información de calidad, exacta, oportuna y relevante.
La Inteligencia Artificial (IA) trata de conseguir que los ordenadores simulen la inteligencia humana; es una rama de las ciencias computacionales encargada de estudiar modelos de cómputo capaces de realizar actividades propias de los seres humanos, en base a dos de sus características primordiales: el razonamiento y la conducta. La inteligencia artificial es el ¨esfuerzo de desarrollar sistemas basados en computadora que se pueden comportar como los humanos con la capacidad de aprender lenguajes naturales, efectuar tareas físicas coordinadas, utilizar un aparato perceptor y de emular la experiencia y la toma de decisiones¨ (Laudon K, 2004). En el momento actual la IA se aplica a numerosas actividades humanas, y como líneas de investigación más explotadas destacan el razonamiento lógico, la traducción automática y comprensión del lenguaje natural, la robótica, la visión artificial y, especialmente, las técnicas de aprendizaje y de ingeniería del conocimiento. Estas dos últimas ramas son las más directamente aplicables al campo de las finanzas pues, desde el punto de vista de gestión organizacional, lo que interesa es construir sistemas que incorporen conocimiento y, de esta manera, sirvan de ayuda a los procesos de toma de decisiones.
En los últimos años, en al ámbito empresarial gracias a la IA, se ha pasado de las herramientas que facilitan o simulan el procesamiento manual de la información a robustos algoritmos que sirven como soporte para la toma de decisiones adecuadas, eficaces y oportunas (Aboueldahab, 2011; Asadi, 2012; Dai, 2012); siendo los más notables los sistemas expertos y las redes neuronales artificiales. Desde hace tiempo los economistas han estudiado e intentado comprender los movimientos de los índices financieros derivados de series económicas. Tanto investigadores como profesionales reconocen que el pronóstico en contexto económico-financiero es una tarea desafiante ya que las series de datos siguen dinámicas complejas, no lineales, caóticas, ruidosas y cambiantes en el tiempo, haciéndolas volátiles, no estacionarias, multifractales, de memoria larga, inestables y de alto riesgo (H. Jiang, 2010; C.Cai, 2012). En las empresas, los estados financieros son objetos de interés desde la óptica predictiva. En especial la modelación de la disponibilidad real de efectivo es una actividad vital para garantizar la permanencia y crecimiento económico de una organización. Para predecir los flujos de efectivo de una forma más acertada, estos se deben desagregar y se debe tener en cuenta el ingreso como variable básica para proyectar la disponibilidad.
MATERIALES Y MÉTODOS
Una característica distintiva en la mayoría de los procesos de las organizaciones, es la generación de eventos sometidos a influencias de factores no predecibles, en los que sus atributos toman forma de series de tiempo. En la predicción de series de tiempo financieras, los modelos lineales tienen una considerable ventaja sobre el resto por la fácil interpretación de sus elementos. A principio de la década de 1980, los modelos empleados para modelar la media de un activo eran los ARIMA o ARIMAX, pero entrada la década de los 90 con los modelos ARCH y Garch, se le da más importancia a la volatilidad que a la media de los datos (Alonso, 2009).
El modelo autorregresivo integrado de media móvil ARIMA introducido por Box y Jenkin ha sido uno de los enfoques más populares utilizado en la predicción (Pai, 2005). En este enfoque se parte del supuesto de que el valor futuro de la variable es una combinación lineal de valores y errores pasados; sin embargo, cualquier grupo de características no lineales lo limita. En 2005 se sugiere el uso de un nuevo modelo denominado Arfima (Bhardwaj, 2006). Las estimaciones usan una variedad de procedimientos estándares que proporcionan mejores predicciones que los modelos de la familia ARIMA-ARIMAX y Garch.
En estudios realizados sobre la volatilidad diaria del índice S&P-100 de Estados Unidos (Liu y Hung, 2010), se compararon los modelos Garch-N, Garch-t, Garch-HT y Garch-SGT con modelos del tipo asimétrico como GJR-Garch y Egarch, arribando a la conclusión de que estos últimos mejoran la volatilidad del pronóstico y demuestran que el componente asimétrico es más importante que la especificación de la distribución cuando hay presencia de asimetría, leptocurtosis y efectos Leverage.
Métodos no lineales de predicción. Machine Learning en el ámbito contable-financiero
El análisis de datos económicos en la era actual está caracterizado por el creciente uso de modelos no lineales de predicción. La teoría econométrica destaca diferentes fuentes potenciales para la presencia de no linealidades y ciclos en los activos financieros. Desde el enfoque del aprendizaje automático, en cada momento t de una data histórica, es posible aplicar modelos de predicción; y en ello la IA y sus aportes desde el Machine Learning (ML) están liderando desde hace unas pocas décadas.
Redes Neuronales Artificiales
En los últimos años se reporta un incremento del uso de las Redes Neuronales Artificiales (RNA) en la predicción de series financieras, ya que parece ser muy eficaz y presenta multitudes de variantes. Una RNA es un modelo de procesamiento de información que es inspirado en el funcionamiento del sistema nervioso biológico. Es un procesador distribuido en paralelo de forma masiva que tiene una tendencia natural para almacenar conocimiento de forma experimental y lo hace disponible para su uso. La ventaja de usar redes neuronales está en el hecho que se pueden separar regiones no lineales de decisión tan complicadas como se deseen dependiendo del número de neuronas y capas.
(Zemke, 1999) utilizó cuatro técnicas del ML para analizar la Bolsa de valores de Varsovia. La tarea consistió en predecir el valor del índice a través de decisiones binarias; es decir pronosticar la proyección (aumento o disminución respecto al valor actual) del índice WIG en la semana siguiente. Las técnicas utilizadas fueron: redes neuronales artificiales, clasificador bayesiano, K-nearest neighbor y K-nearest neighbor prediction scrutinized. Se concluyó que con las RNA se obtuvieron las mejores predicciones debido a que la bolsa de valores está dominada por la no linealidad en los datos. En el mismo año, Lee y Jo desarrollaron un intérprete gráfico para predecir el mercado, al que llamaron Candlestick Chart Analysis Expert System (Lee y Jo, 1999). Los resulta dos experimentales obtenidos revelaron que el modelo tenía un porcentaje de aciertos promedio de 72%, lo cual ayuda a los inversores a obtener mayores benefi cios de su inversión en acciones. Guresen, Kayakutlu y Daim observaron que en la mayoría de los casos los mo delos de redes neuronales permiten obtener mejores resultados que otros métodos (Guresen, 2011). Los modelos que se compararon en su trabajo son multi-layer perceptron (MLP), dynamic artificial neural network (DAN2) y un modelo híbrido de redes neuronales y Garch, con los valores diarios del índice Nasdaq desde el 7 de octubre de 2008 hasta el 26 de junio de 2009. El rendimiento de los modelos se evaluó a través del error cuadrado medio y la desviación absoluta media, obteniéndose que el clásico modelo MLP supera a los demás al obtener mejores resultados. Existe una gran cantidad de estudios que incluyen modelos de redes neuronales artificiales, sin embargo, las RNA tienen limitaciones en el aprendizaje de patrones debido a que los datos de las series financieras por lo general tienen dimensionalidad compleja, gran ruido y en algunos casos volatilidad considerable (Kim y Han, 2000).
Máquinas de Soporte Vectorial
Las Máquinas de Vectores Soporte (SVM) es una de las técnicas más poderosas del aprendizaje automático, que a pesar de su sencillez ha demostrado ser un algoritmo robusto y que generaliza bien en problemas de la vida real (Gala Garcia, 2013). Se considera una alternativa eficiente ante las limitaciones de las RNA frente a la dimensionalidad y ruido en los datos. Hay estudios que reportan que las SVM superan en precisión a los modelos autorregresivos de medias móviles, las redes neuronales artificiales y los sistemas adaptativos de inferencia neuro-difusos (Jaramillo, 2015). Fueron desarrolladas por Vapnik y sus colaboradores en el marco de la Teoría de Aprendizaje Estadístico (SLT) (Vapnik et al, 1999). Usa modelos lineales para implementar clases con separaciones no lineales al transformar el espacio de entrada en un nuevo espacio. Han sido estudiadas intensamente en los últimos años y aplicadas exitosamente en gran variedad de temas como: estimación de densidades probabilísticas, y la predicción de series de tiempo (Cuevas, 2010).
En principio las SVM están indicadas para ser usadas como clasificadores binarios. La tarea de clasificación está dividida en dos etapas: la fase de aprendizaje automático y la fase de reconocimiento. En la primera se selecciona el conjunto de entrenamiento, se extraen los atributos y características del espacio de entrada y se entrena el clasificador. El entrenamiento da como resultado un conjunto de parámetros w que define al clasificador y un hiperplano de separación óptimo (HSO) de margen máximo que representa las regiones de clasificación. En la fase de reconocimiento el modelo del clasificador entrenado, asigna a los datos que se le presenta una de las clases según la región de clasificación en la que hayan sido mapeado los nuevos datos. El aprendizaje según (Farías, 2011), se logra mediante la búsqueda de alguna dependencia funcional entre un conjunto de vectores con los datos de entrada y salida, permitiendo así encontrar un espacio lo más amplio posible con lo cual se puedan separar los datos pertenecientes a una clase u otra. La esencia de las SVM puede ser entendida sin el uso de fórmulas, para lo cual es necesario el conocimiento de cuatro conceptos básicos: el hiperplano de separación, el hiperplano óptimo, el margen suave y la función kernel o núcleo.
SVM lineales. Hiperplano de separación óptimo y margen máximo
Las SVM poseen una gran capacidad para aprender a partir de un conjunto de N muestras experimentales denominado conjunto de entrenamiento:
{(x1, y1), (x2, y2), . . ., (x n , y m )}
Donde cada muestra (x i ,y i ) para i=1…N está formado por un vector de n características x i ϵ R n y a una etiqueta y i ϵ R que indica la clase {±1} a la que pertenece cada muestra. El objetivo es encontrar la función f: R n → {±1} que separe los datos en dos clases y que clasifique correctamente nuevas muestras perteneciente al conjunto de pruebas.
En un problema linealmente separable existen muchos hiperplanos que pueden clasificar los datos, pero las SVM no hayan uno cualquiera sino el único que maximiza la distancia entre el y el dato más cercano de cada clase (Figura 1). El hiperplano de separación óptimo (HSO) está definido por el margen máximo de separación entre las dos clases. Tomando como referencia la notación de la Figura 1, existen dos hiperplanos que definen las muestras a ambos lados de cada clase: w*x+b=+1 y w*x+b=-1 que son paralelos al HSO w *x+b=0. El margen máximo está dado por la distancia entre los hiperplanos paralelos y el HSO, cuyo resultado geométrico equivale a 2/||w||. El vector de pesos w contiene la ponderación de cada atributo, indicando qué tanto aportan en el proceso de clasificación.
Hallar el mejor hiperplano de separación es un clásico problema de maximización con restricciones lineales, quedando como
pudiendo ser resuelto aplicando los multiplicadores de Lagrange:
La búsqueda de la solución es preferible en el espacio dual buscando que se dependa únicamente del producto escalar de los patrones de entrada, lo cual simplifica los cálculos:
Esta formulación del problema satisface las condiciones de Karush-Kuhn-Tucker (KKT) y por tanto se tienen las condiciones necesarias y suficientes para que un valor extremo exista (H. Mora, 2001). De la expresión en forma matricial
donde se utiliza el vector unitario f= [11…1] T y mediante cualquier método de optimización se halla el vector de multiplicadores α0 = (α 0 1, α 0 2, α 0 3… α 0 N ) para finalmente determinar el vector normal w 0 y el bias b 0 del HSO
esto indica que w 0 se puede expresar como combinación lineal de N vectores de entrada. De las condiciones KKT se desprende que gran parte de los multiplicadores de Lagrange α0 son cero, por lo que una menor cantidad de vectores del conjunto de entrada N sv participan de la combinación lineal que origina a w 0: los vectores de soporte. En la expresión anterior X r y X s son un par de vectores soporte, uno de cada clase. La expresión final del clasificador buscado finalmente seria
donde el signo resultante indicará la clase a la cual pertenece un dato determinado. Nótese que la sumatoria no se realiza sobre todos los puntos de entrenamiento N, sino sobre los que son vectores soporte (SV) siendo el número de estos por lo general mucho menor.
SVM no lineales con Kernel
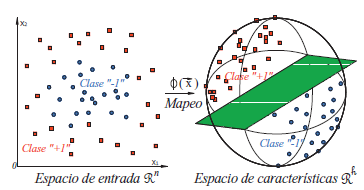
La mayoría de los eventos reales no son separables linealmente por lo que se dificulta la definición del HSO. La Figura 2 muestra un conjunto de datos donde no pueden ser separados linealmente por un hiperplano en R n , pero si en un espacio de mayor dimensión R h ( Statnikov et al., 2011).
Cuando no existe una apropiada superficie lineal de decisión en el espacio original de los datos, se considera un mapeo del vector de entrada en un espacio de mayor dimensión R h llamado espacio de características, que está dotado de producto escalar. Eligiendo la transformación adecuada R n → R h se realiza el mapeo y se busca el HSO siguiendo la metodología del apartado anterior que será lineal en R h , pero representa un espacio no lineal en R n . Este tipo de proyección hacia un espacio de característica es a través de las funciones denominadas kernels: K(x i ,x k )=ᶲ(x i )*ᶲ(x k ). Las funciones kernel permiten realizar las operaciones algebraicas en R h de manera eficiente y sin conocer a la transformación ᶲ. Así, en principio cualquier técnica de análisis multivariado para datos x ϵ R n que se pueda reformular en un algoritmo computacional en términos de productos escalares, se puede generalizar a los datos transformados utilizando las funciones núcleos.
Existen varias funciones kernel o núcleos, destacando las siguientes cuatro, consideradas básicas:
Kernel lineal:
K(x i ,x j )=x i T * x j
Kernel polinomial:
K(x i ,x j )=(p+ϒ x i T * x j ) d , ϒ>0
Kernel gaussiano RBF:
K(x i ,x j )=exp(-ϒ ||x i -x j || 2 ), ϒ>0
donde ϒ, d y p son parámetros de los núcleos y * producto escalar. Finalmente para el caso no lineal la expresión del clasificador buscado usando un kernel conveniente K seria
En general, el núcleo RBF es una razonable primera elección. Este núcleo no lineal mapea las muestras a un espacio de dimensión más grande, y a diferencia del núcleo lineal puede ayudar cuando la relación entre las etiquetas de las clases y las características es no lineal (Lio, 2016).
Método de trabajo desarrollado
La Empresa en la que se realiza la investigación es perteneciente a la Unión Eléctrica. La Empresa de Mantenimiento a Centrales Eléctricas (EMCE), como su nombre lo indica, su responsabilidad en el sistema electro-energético cubano (SEN) fundamentalmente es ofrecer mantenimiento y servicios técnicos a las Centrales Térmicas desplegadas en el territorio nacional. El desplazamiento continuo y poco predecible de las acciones de mantenimiento en el SEN producto al comportamiento fortuito de las averías, exige de la dirección de la entidad una planificación acertada de los financiamientos hacia las acciones de mantenimiento con una frecuencia semanal. La hipótesis que conduce la investigación es la siguiente: Un pronóstico adecuado sobre la proyección que experimentarán los ingresos, proporcionará un punto de partida adecuado para el diseño de estrategias efectivas para financiar las acciones de mantenimiento en el SEN, sin poner en riesgo el pago de las obligaciones con proveedores, el apoyo de las inversiones en proceso, y la disponibilidad corriente de efectivo para abordar eventualidades. La metodología de trabajo está inspirada en un proceso de KDD o minería de datos: ¨proceso no trivial de identificación en los datos de patrones válidos, nuevos, potencialmente útiles y finalmente comprensibles¨. La minería de datos busca la extracción de conocimiento explicito, potencialmente útil que permanece oculto en grandes volúmenes de datos, con el fin de encontrar patrones o reglas y resumirlos de forma que sean fácilmente entendibles por parte de un usuario (Hand, 2001).
Selección del conjunto de datos y pre- procesamiento
Los datos necesarios fueron obtenidos del estado de cuentas bancarias de la organización en el periodo 2016-2017. La ocurrencia de las operaciones de débitos es aleatoria, para lo cual fue necesario normalizar la serie de tiempo hacia una frecuencia semanal a través del cómputo de los ingresos acumulados al final de cada semana, arribando al arreglo ordenado y espaciado con frecuencia semanal x i . Para completar la etapa de pre-procesamiento se trabajó en la especificación de y i : etiquetas para cada vector de n característica x i ϵ R n . Las etiquetas y i ϵ R toma los valores {±1} identificando los incrementos de los ingresos respecto a la semana anterior (+1), en lo adelante proyección alcista; y las disminuciones (-1), en lo adelante proyección bajista (PB), calculándose con la siguiente expresión:
y i =sign (xi - x i-1 )
Finalmente, el conjunto de entrenamiento se conformó con las etiquetas y los ingresos con retardos de hasta cuatro semanas (x t-1 .. x t-4 ,yi), tomando como supuesto fundamental que la proyección de los ingresos para un periodo t+1 está en función de los valores pasados de t.
Diseño e implementación de la máquina de soporte vectorial
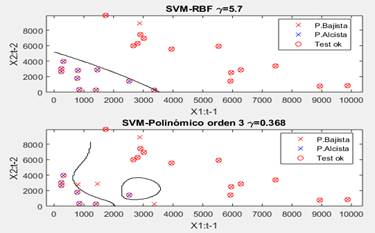
El diseño de la SVM pasa por la elección del tipo de kernel, el algoritmo para resolver el problema de programación cuadrática que nos lleva a la construcción adecuada del HSO, y la heurística para determinar el ajuste óptimo de los parámetros del núcleo. Para el caso que nos ocupa se utilizará el método de entrenamiento denominado SMO (Optimización Mínima Secuencial o Sequential Minimal Optimization). Su rendimiento es muy bueno para el caso de SVM no lineales y pocos datos en el conjunto de entrenamiento (Castro, 2010). El kernel usado será el gaussiano o RBF siendo ϒ el parámetro a sintonizar a partir de métodos de validación cruzada (crossvalidation), por ser el más utilizado y con mejor resultados. Se hicieron comparaciones del desempeño con otros tipos de kernel como el lineal y polinomial de varios órdenes.
RESULTADOS Y DISCUSIÓN
Los resultados obtenidos están en función de las n característica x i del conjunto de entrenamiento y el conjunto de prueba. En la fase de aprendizaje se entrenaron cuatro SVM con kernel diferentes, algoritmo SMO y método de validación cruzada para sintonizar el parámetro del núcleo. En el conjunto de entrenamiento para cada uno de los modelos entrenados se incrementó la dimensionalidad desde dos hasta cuatro rezagos de la variable input.
Elección del mejor clasificador para pronóstico
El modelo óptimo resultó con un kernel de tipo gaussiano para ϒ= 5.7 Y dimensionalidad R 2 , R 3 y R 4 indistintamente; es decir, el uso de dos hasta cuatro variables delay como input al modelo no hace la diferencia en su precisión. La elección definitiva hacía del modelo construido sobre R 2 obedece a los criterios siguientes (Flores, 2015):
Una representación con menos atributos realza el poder predictivo del modelo de clasificación disminuyendo su complejidad y reduciendo el riesgo de Overfitting (sobreajuste) causado por la maldición de la dimensionalidad.
Permite una mejor interpretación del clasificador, lo que es particularmente importante debido a que muchos profesionales consideran que las técnicas de machine learning son cajas negras y se rehúsan a emplear estos métodos debido a su complejidad.
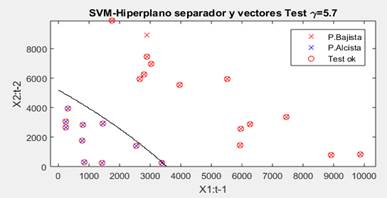
La Figura 3 muestra el hiperplano sobre los datos de entrenamiento en un espacio determinado por los ingresos de las dos últimas semanas, resultando el error de generalización de 23.31 %. La SVM construye dos regiones de clasificación a partir del HSO, permitiendo un determinado número de muestras mal clasificadas a ambos lados del hiperplano sin comprometer el margen máximo de separación, como principal garantía de una buena generalización. Los SV que determinan la construcción del HSO se muestran circulados en la gráfica.
En la etapa de prueba los resultados del clasificador son mejores que en la etapa de aprendizaje. Se le presentó 24 muestras nuevas al clasificador seleccionado para evaluar su desempeño y como se puede apreciar en la Figura 4, solo confunde una proyección bajista con alcista, para un error de generalización de 4.2 %. De manera que el modelo encontrado es capaz de predecir si los ingresos en el próximo periodo se incrementarán (alcista) o disminuirán (bajista) respecto al periodo anterior, con una tasa de error inferior al 5%. La Tabla 1 muestra el mejor desempeño sobre el conjunto de entrenamiento de diferentes SVM con kernel del tipo lineal y polinomio en comparación con el RBF o gaussiano.
Se evidencia el buen desempeño de todos siendo más notorio el construido sobre el kernel RBF con 95.8%. La SVM con núcleo lineal alcanzó un menor error de generalización a mayor dimensionalidad, sin embargo, con el uso de kernel polinómico de orden 3 se obtiene similar desempeño y la dimensionalidad es menor. Para el modelo con kernel gaussiano, el aumento de la dimensionalidad en la etapa de entrenamiento no aportó mejoras en el rendimiento final del modelo. La Figura 5 muestra como la complejidad del HSO en ocasiones no es indicativa de la capacidad discriminativa de las SVM. El hiperplano del modelo con kernel polinómico de tercer orden presenta un grado de complejidad mayor dando la sensación de tener mejores propiedades de generalización; no obstante, su error de generalización (12.5 %) es superior al de la SVM con kernel RBF, la que exhibe un HSO visualmente menos complejo y un error de generalización menor.
Herramienta gráfica para visualizar resultados de pronósticos sobre la proyección de variables económicas: graph of prognostic projections
La interpretación de una proyección alcista o bajista de un indicador económico a través de gráficos como las mostrados en las Figura 3 y Figura 4 pueden no ser de fácil comprensión para los decisores en una organización que no están familiarizados con los conceptos del Machine Learning y de algoritmos como las SVMs. Es por ello que se hace necesario el uso de otra herramienta gráfica que muestre de forma compacta los resultados de un modelo de pronóstico como los obtenidos en esta investigación. Las proyecciones o movimientos que experimentan los ingresos en nuestro caso de estudio, están en función de combinaciones no lineales de los valores pasados;
y i =sign (f (xi -1, x i-2… x i-n )),
y i ϵ R indica la clase {±1}, donde +1 significa que los ingresos en el periodo x i > x i-1 y -1 verifica que x i < x i-1 ; y M = f (xi -1… x i-n ) es el modelo de predicción diseñado. De manera que podemos definir un pronóstico en función del periodo anterior y el modelo de predicción de la siguiente forma:
P i = y i * x i-1
donde x i-1 determinará el límite inferior para las proyecciones alcistas, o límite superior para las proyecciones bajistas. Este límite aportará información en el proceso de interpretación.
En la Figura 6, se visualiza la interpretación de los conceptos anteriores en la gráfica que denominamos: graph of prognostic projections (GPP). Se proyecta sobre el eje de las ordenadas el valor P, donde el signo obtenido refiere la dirección de la proyección (alcista o bajista) del pronóstico, y el |P| el límite que servirá de referencia para la interpretación final del resultado.

Fig.6 Gráfico para el pronóstico de proyecciones sobre variables económicas, GPP. a) Proyecciones pronósticos sobre el conjunto de prueba. b) Validación de las proyecciones pronósticos sobre el conjunto de prueba.
En a) el pronóstico resultante para la séptima semana es 3,374 millones de pesos, lo que significa que se pronostica para ese momento un incremento del ingreso respecto al periodo anterior siempre mayor a este valor. Para el periodo siguiente P= -7450, significando así una disminución de los ingresos respecto al periodo anterior y fijándose un límite máximo de ingreso de 7,450 millones de pesos. En b) se comparan los resultados de cada una de las predicciones con lo valor reales obtenidos R i (barras azules) en cada semana que compone el conjunto de prueba. Se verifica que para cada P i > 0 (proyecciones alcistas), R i > P i , obteniéndose un acierto del 100%; no así en la proyección bajista (P i < 0) donde se cumple para todos los casos la condición R i < P i excepto el vigésimo periodo, para un acierto de 95.8%.
CONCLUSIONES
La Inteligencia Artificial como rama revolucionaria de la Ciencia de la Computación, constituye una herramienta robusta para enfrentar tareas de pronóstico y clasificación en actividades tan sensibles como la planificación financiera. En ello, la variable ingreso constituye un indicador económico indispensable para modelar la disponibilidad de efectivo en una organización y proyectar sus movimientos futuros, en aras de lograr un proceso de toma de decisiones efectivo con un mínimo de riesgo.
Utilizando elementos del análisis univariado de series de tiempo, se implementa el algoritmo Máquinas de Soporte Vectorial (SVM) para pronosticar el movimiento que percibirán los ingresos en la Empresa de Mantenimiento a Centrales Eléctricas para el próximo periodo, y se concluye:
Las SVM son adecuadas para enfrentar problemas de clasificación y predicción sobre series de tiempo de carácter financiero.
El modelo seleccionado, construido sobre el kernel del tipo gaussiano supera a los del tipo lineal y polinómico.
Para el caso de estudio abordado, se pudo constatar que la complejidad del HSO obtenido por algún tipo de kernel en el entrenamiento, no garantiza ser el de mejor desempeño frente a nuevos datos.
Como novedad, se diseña una herramienta visual (graph of prognostic projections) para interpretar los resultados obtenidos por el algoritmo SVM para pronosticar la proyección de los ingresos. Su aplicación es independiente del modelo de predicción que se use sobre variables económicas.