Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
La toma de decisiones es un proceso de selección entre cursos de alternativas, basado en un conjunto de criterios, para alcanzar uno o más objetivos (HERBERT, 1960), (FINCOWSKY, 2011). El proceso decisional se compone de cuatro etapas fundamentales (MARTÍNEZ, 1998):
Diagnóstico: Consiste en detectar cuál es el problema o conjunto de problemas que afectan el proceso.
Diseño: Modela las diferentes alternativas gracias a las cuales, a priori, es posible solucionar el problema diagnosticado. Deben cumplirse tres principios: Exclusividad, donde una estrategia supone el rechazo de las demás. Exhaustividad, se deben incluir todas las posibles formas de actuación. Viabilidad, deben ser viable desde el punto de vista, técnico, operativo, financiero, etc.
Elección: Fase en la cual es seleccionada la mejor estrategia o alternativa del conjunto.
Revisión: Se lleva a cabo un análisis sobre el grado en el que la estrategia seleccionada y ejecutada ha conseguido resolver el problema.
Los problemas de toma de decisiones pueden ser clasificados según el ambiente de decisión como problema de toma de decisiones en ambiente de certidumbre, ambiente de incertidumbre y ambiente de riesgo (TAMES and CAMPOS 2020). En un problema de toma de decisiones en ambiente de certidumbre se conocen con precisión los elementos que intervienen en el problema donde es posible asignar un valor exacto de utilidad a la alternativa involucrada.
Para un problema de toma de decisiones en ambiente de incertidumbre no se cuenta con la información necesaria o esta es imprecisa, se asocia a criterios subjetivos del problema que se analiza. El resultado de la inferencia está condicionado por el método y configuración utilizada considerandos un problema complejo de decisión.
En procesos de toma de decisiones, representar la causalidad permite modelar la causa o efecto de un determinado evento (MARTÍNEZ, FRANCISCO ZAMORA 2012). Existen diferentes tipos de causalidad donde cada modelo causal se puede representar por un grafo (GOODIER et al, 2010), (GONZÁLEZ, 2013) tal como representa la Figura 1.
La causalidad se expresa mediante una relación precisa, en la vida cotidiana las personas son capaces a partir de su conocimiento empírico, de elaborar representaciones mentales de fenómenos reales, la fiabilidad de la inferencia estaría condicionada por el nivel de experticia para interpretar la realidad, por lo tanto, si se modela correctamente la causalidad de un determinado concepto, es posible predecir su efecto.
Para la representación de la causalidad desde el punto de vista computacional, la literatura científica recoge fundamentalmente dos técnicas: las Redes Bayesianas (PEARL 2009) y los Mapas Cognitivos Difusos (FCM) (PAPAGEORGIOU and SALMERON 2013), para el contexto de la presente investigación se utilizará este último.
Los FCM son una técnica que permite representar las relaciones causales de diferentes conceptos, propuesta por Kosko (KOSKO 1986) como una extensión de los Mapas Cognitivos empleando valores difusos en un intervalo de [-1,1] (SALMERON 2009). Los FCM se representan mediante modelos difusos con retroalimentación para representar causalidad (GLYKAS and GROUMPOS 2010).
Cada nodo constituye un concepto causal, esta característica hace que la representación sea flexible para visualizar el conocimiento humano. La matriz de adyacencia se obtiene a partir los valores asignados a los arcos (LEYVA-VÁZQUEZ et al. 2013),(GONZALO NÁPOLES et al. 2018) tal como expresa la Figura 2.
En el FCM existen tres posibles tipos de relaciones causales entre conceptos (GONZALO NÁPOLES et al. 2018):
Wij > 0, Indica una causalidad positiva entre los conceptos Cj y Ci. Es decir, el incremento (o disminución) en el valor de Cj lleva al incremento (o disminución) en el valor de Ci.
Wij < 0, Indica una causalidad negativa entre los conceptos Cj y Ci. Es decir, el incremento (o disminución) en el valor de Cj lleva al disminución (o incremento) en el valor de Ci.
Wij = 0 , Indica la no existencia de relaciones entre los conceptos Cj y Ci.
Entre los diferentes criterios para la toma de decisiones, se destacan cinco criterios clásicos: Optimista, Pesimista o de Wald, el criterio de Hurwicz, entre otros.
Sin embargo, los FCM no contemplan al conjunto de criterios clásicos empleados para la toma de decisiones, lo que imposibilita la evaluación de habilidades desde diferentes escenarios como pudiera ser, el optimista o pesimista. Un escenario de implementación pesimista, representaría la naturaleza menos favorable de la inferencia, mientras que el escenario optimista representaría la inferencia más favorable. La presente investigación tiene como objetivo la implementación de un operador de agregación de información que integra la selección de tres criterios clásicos para la toma de decisiones
MÉTODOS O METODOLOGÍA COMPUTACIONAL
Los operados de agregación son funciones matemáticas utilizadas en procesos de toma de decisiones (GRAU and GRAU 2012), (MAR et al. 2016) combinan más de un valor en un dominio D y devuelven un valor único. Dentro de los principales operadores para la agregación de información se encuentra la media aritmética y media ponderada (PÉREZ 2014), (MAR et al. 2015) tal como se define a continuación:
Definición 1. Un operador WA es una función 
de dimensión n si tiene asociado un vector de pesos
, con 
y 
, expresado de la siguiente forma:
Donde 
representa la importancia de la fuente 
.
Un operador de agregación de información (OWA Ordered Weighted Averaging por sus siglas en Inglés), Media Ponderada Ordenada propuesto por (YAGER 1988), permite unificar los criterios clásicos de decisión de incertidumbre en una expresión (FILEV and YAGER 1998).
Definición 2. Un operador OWA es una función de dimensión n si tiene un vector asociado W de dimensión 
con y , de forma tal que:
donde
es el j-ésimo más grande de los 
.
Cada familia de operadores es utilizada en diferentes contextos. Existen varias formulaciones de operadores de agregación que unifican los operadores WA y OWA combinando las ventajas de ambos (MERIGÓ and GIL 2010), (DAVID LUIS and JULIO CÉSAR 2014).
Propuesta de operador de agregación de información
Para la presente investigación se empleó el operador (Ordered Weighted Averaging Weighted Averaging OWAWA) debido a su elevada flexibilidad (MERIGÓ 2008), (MAR et al. 2017). Además de unificar los operadores OWA y media aritmética WA, permite reflejar el grado en que se quiere considerar cada uno de ellos.
El autor extiende la definición del operador OWAWA para el trabajo con múltiples funciones por selección en su entrada 
:
Definición 3. Sea un vector de pesos de dimensión n de forma tal que y , relacionado con el operador WA y 
un vector de peso de dimensión n, con una función de configuración
de modo que 
y 
, tal que:
donde : representa la función resultante influenciada por una función inicial de configuración para los atributos de 
.
Conf: representa el comportamiento asumido por los a partir de la configuración .
: vector de pesos de dimensión n influenciado por la función de configuración de los 
.
: es el j-ésimo influenciado por una función inicial de configuración de las Preferencias en j.
La función de configuración 
, representa una agrupación de criterios clásicos para la toma de decisiones para lo cual se utilizan tres criterios fundamentales y se comporta de la siguiente manera:
Para =1: representa un estado de optimismo. Esta función es recomendada para los casos donde las prácticas de laboratorios diseñadas no representan alto grado de complejidad y posee alto grado de tolerancia a fallo. El optimismo representa el estado de la naturaleza más favorable, es conocido como máximo y se formaliza tal como muestra la ecuación 4:
Para =2: representa el estado Pesimista o de Wald: Propuesto por Wald en 1950 (WALD 1950), representa el estado de la naturaleza más desfavorable escogido para cada alternativa. Esta función es recomendada para los casos donde las prácticas de laboratorios diseñadas representan alto grado de complejidad y se requiere que las alternativas demuestren alto grado en sus habilidades. Este método se conoce comúnmente como maximin. Se formula tal como muestra la ecuación 5:
Para =3 representa un estado medio conocido como criterio de Hurwicz. Propuesto por Hurwics en 1951 (HURWICZ 1957), se puede considerar como una combinación entre el criterio optimista y el criterio pesimista. Consiste en ponderar un coeficiente de optimismo y otro de pesimismo al mejor y peor caso respectivamente, se suman los dos valores y se escoge aquella alternativa que proporcione un mayor resultado. Se formula tal como muestra la ecuación 6:
Entonces decisión = Criterio Optimista.
Entonces decisión = Criterio Pesimista.
A partir de la obtención de , se determina mapea el umbral obtenido en la agregación de la información tal que 
haciéndose corresponder con los valores lingüísticos expresados en la Figura 3.
RESULTADOS Y DISCUSIÓN
En la presente sección se presenta un ejemplo práctico de la aplicación del operador de agregación de información, la propuesta permite modelar un problema de toma de decisiones donde es posible analizar diferentes comportamientos.
Descripción del problema
El diagnóstico de habilidades en plataformas que utilizan aprendizaje electrónico y específicamente en los Sistemas de Laboratorios a Distancia, supone un problema de clasificación a solucionar debido al grado de incertidumbre presente el proceso.
Cuando se presenta un conjunto de prácticas de laboratorios que pueden ser desarrolladas por un grupo de estudiantes, que a su vez requieren de un conjunto de habilidades para poder realizarlas, se requiere clasificar si los estudiantes pueden realizar o no la práctica apoyado en su base de conocimiento.
Si se tiene un grupo de personas o alternativas que se necesita saber si pueden realizar las prácticas de laboratorios , que se desean diagnosticar a partir de un conjunto de requisitos o habilidades 
El diagnóstico de habilidades (DH), se define como la tupla 
, donde
Escenario de implementación
A partir de las siguientes habilidades H que serán evaluadas:
H1: Obtener modelos matemáticos dinámicos de sistemas físicos sencillos por vía analítica.
H2: Analizar sistemas de control no lineales simples mediante la elaboración de modelos matemáticos a partir de los datos de sus parámetros y estructura.
H3: Aplicar técnicas de identificación en los dominios del tiempo y la frecuencia para la obtención del modelo matemático de sistemas.
H4: Validar modelos obtenidos aplicando técnicas de identificación.
H5: Elaborar esquemas físicos y en bloques funcionales de sistemas de control.
H6: Simular mediante técnicas de computación sistemas físicos.
H7: Evaluar el comportamiento de sistemas físicos simples mediante técnicas de simulación. Que poseen un conjunto de relaciones causales expresada mediante la matriz de adyacencia M = M{HiHj} que representa el valor causal de la función del arco, el nodo Hi que implica Hj representando un vértice. Hi incrementa causalmente a Hj si Mij = -1 y no implica causalmente sí Mij = 0.
Quedando expresada tal como muestra la Tabla1.
A partir de la matriz de adyacencia se obtienen los valores del grado de entrada (Id), grado de salida (od) y la normalización de los indicadores.
El grado de entrada (Id) representa un arreglo de valores que expresa una función de comparación de un indicador Hi respecto al resto de los indicadores Hpj tal que Hpj expresa el desplazamiento vertical sobre los elementos recorridos por j, se obtiene mediante la siguiente ecuación.
El grado de salida (od) representa por su parte un arreglo de valores que expresa una función de comparación de un indicador Hj respecto al resto de los indicadores Hi tal que Hi expresa el desplazamiento horizontal sobre los elementos recorridos por i, se obtiene mediante la siguiente ecuación.
La normalización de los indicadores tiene lugar a partir de que los valores obtenidos mediante Odi, Idi representan vectores que no se encuentran en un dominio de valores discreto 
. La normalización es representada mediante una función promedio tal que , se obtiene como resultado Tabla 2
Se genera una agrupación de los cuestionarios evaluativos obtenidos de forma aleatorios tal como expresa la ecuación-
Donde:
Agrupar: representa la función resultante de la agrupación de los cuestionarios.
Pa: almacena los t cuestionarios generados por RandonCe.
RandonCe: función de generación de valores aleatorios . comprendido entre 1 y el total de cuestionarios elaborados.
La obtención de las preferencias de las alternativas se hace a partir de la evaluación que se obtiene de las respuestas de los cuestionarios donde:
Para cada alternativa A se le hace corresponder un paquete de cuestionarios Pax que una vez repuesto devuelve un arreglo Prey con las preferencias sobre las habilidades.
Para el proceso de inferencia sobre el acceso a las prácticas de laboratorios se parte de:
Donde:
: representa el umbral sobre las habilidades
: representa el operador de agregación y clasificación a utilizar
donde : representa la función resultante influenciada por una función inicial de configuración 
para los atributos de 
.
Conf: representa el comportamiento asumido por los a partir de la configuración 
.
: vector de pesos de dimensión n influenciado por la función de configuración de los 
.
: es el j-ésimo influenciado por una función inicial de configuración de las 
.
Resultados Y Análisis
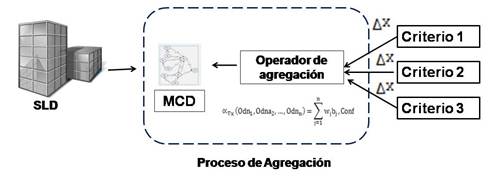
La Figura 4 representa un esquema para la implementación del operador de agregación propuesto, se utiliza como parámetro de entrada los valores del grado de salida normalizada obtenidos de la matriz de adyacencia y el conjunto de preferencia obtenido por las alternativas en el proceso de evaluación.
La Tabla 3 registra los valores resultantes de la aplicación del operador de agregación para los tres posible escenarios definidos por el selector 
las alternativas representan el conjunto de individuos que participan en el proceso, las preferencias representa la evaluación resultante de los cuestionarios evaluativos resueltos y el selector define el comportamiento del operador de agregación a partir de los tres criterios definidos en las ecuaciones 4,5 y 6.
Para el análisis de los resultados se realiza una valoración sobre el comportamiento de los tres escenarios implementados (optimista, pesimista y de Hurwicz) en el operador de agregación.
La Figura 5 presenta el escenario de aplicación 1, donde se utiliza el criterio optimista para el razonamiento en el proceso de toma de decisiones. Para el escenario propuesto, 4 de las alternativas poseen una evaluación de habilidades igual o superior a un conocimiento medio.
La Figura 6 presenta el escenario de aplicación 2, donde se utiliza el criterio pesimista para el razonamiento en el proceso de toma de decisiones. Para el escenario propuesto, 3 de las alternativas poseen una evaluación de habilidades igual o superior a un conocimiento medio.
La Figura 7 presenta el escenario de aplicación 3, donde se utiliza el criterio de Hurwicz para el razonamiento en el proceso de toma de decisiones. Para el escenario propuesto, 4 de las alternativas poseen una evaluación de habilidades igual o superior a un conocimiento medio.
La Tabla 4 presenta un resumen del comportamiento de las habilidades de las alternativas según el comportamiento asumido por el operador de agregación. Para 
=1 responde a la naturaleza más favorable, este escenario es recomendado cuando se quiere que los individuos que intervienen en un proceso de toma de decisiones sean favorecidos. Para =3representa un estado que responde a un comportamiento similar a la realidad. Por otra parte para =2 representa la naturaleza más desfavorable.
Si se quiere que los individuos que intervienen en un proceso de toma de decisiones ganen confianza en sí mismo, la aplicación de un proceso de selección en un estado optimista ayudaría en este sentido, la Tabla 4 para el escenario 1 muestra que 4 de las alternativas poseen evaluación satisfactoria y 2 de ellos son evaluados de alto. Si por el contrario se quiere que los individuos tengan objetivos más retadores y se incentive la superación continua la aplicación de un estado pesimista contribuiría a fomentar nuevos desafíos, la Tabla 4 para el escenario 2 muestra que 2 de las alternativas poseen evaluación de bajo y 3 de ellos son evaluados de medio.
CONCLUSIONES
El operador propuesto, permite unificar varios criterios para la toma de decisiones integrado en Mapa Cognitivo difuso para procesos de la toma de decisiones.
La aplicación del operador en la evaluación de habilidades, permitió la incorporación de varios criterios para la toma de decisiones, los cuales se aplican en función del escenario deseado. Se demostró experimentalmente que el comportamiento asumido por el operador, determina el resultado de la evaluación aplicada.
Con trabajos futuros se proyecta la implementación de otros criterios de los existentes para la toma de decisiones que sean posibles integrar en Mapas Cognitivos Difuso extendiendo además su aplicación en otras áreas del conocimiento.
