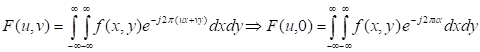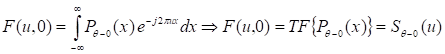INTRODUCCIÓN
Una de las áreas de investigación de la inteligencia artificial que en las últimas décadas se ha desarrollado, sin duda, es el Procesamiento Digital de Imágenes (PDI). Obviamente esto sucede debido a que cada día la información visual es más importante y abundante, y es por eso que se necesitan técnicas que manipulen adecuadamente esa información. El campo del PDI se refiere al estudio de técnicas que permitan de alguna forma mejorar una imagen, de manera que pueda ser utilizada en etapas posteriores de procesos de visión, como por ejemplo análisis de imágenes. Las pruebas de imagen constituyen un elemento esencial para el diagnóstico temprano de infinidad de patologías y para la realización de un dictamen médico rápido y eficaz, por eso que es muy importante e indispensable el tratamiento de imágenes en la obtención de estudios de calidad, para establecer un diagnóstico preciso, diferenciar y no omitir patologías describir certeramente un hallazgo y realizar su seguimiento.
El análisis de imágenes médicas es en la actualidad una herramienta imprescindible para el diagnóstico médico, debido a la cantidad de información que brindan estas imágenes sobre estructuras anatómicas de interés como la forma, posición, orientación, simetría, relación entre estructuras y órganos, así como la variación de dichas estructuras y órganos en presencia de diferentes patologías. Un repaso muy interesante de la evolución de las técnicas de análisis y procesamiento de imagen médica desde los años 80 puede encontrarse en (Esquivel, y otros, 2018). Existen varias aplicaciones que consisten en procesar imágenes en varios sectores como militar, en la agronomía, en la medicina, en la meteorología, en satélites.
En el sector de la salud se pone de manifiesto en el uso de las imágenes obtenidas por diferentes modalidades de adquisición como en radiología, tomografía computarizada (TC), radiología digital, fluoroscopio, con el fin de poder detectar o diagnosticar enfermedades. La TC es una técnica que utiliza los rayos X, y realiza cortes al paciente para obtener imágenes, estas imágenes pueden a presentar distorsiones por movimiento del paciente o la existencia de alguna anomalía externa lo que se llaman artefactos de endurecimiento del haz, lo que representa una de las preocupaciones de los técnicos de la salud, ya que se les dificulta realizar un diagnóstico más preciso.
Los artefactos plantean un problema grave. Ocasionalmente, pueden alterar la interpretación de las imágenes, simulando una condición patológica. Un artefacto se define como una distorsión, adición o error en una imagen que no tiene relación con el sujeto o región anatómica estudiada. Como término se deriva de las palabras latinas artis (artificial) y actum (efecto) y refiere a un efecto artificial que altera la calidad y fidelidad de una imagen, pudiendo encubrir una patología o crear hallazgos falsos y se dividen según su origen, aunque, sea cual sea su naturaleza, se observan como rayas, anillos, ruidos y bandas blancas y negras superpuestas (Sartori, 2015).
A partir de la revisión bibliográfica realizada, se aprecian insuficiencias relacionadas con el poco conocimiento que hay con respeto al campo de procesamiento de imágenes y la poca divulgación de documentos donde se propongan los algoritmos que sirvan para desarrollar exitosamente las aplicaciones de procesamiento de imágenes. Además, la descentralización de las referencias bibliográficas y en su mayoría en el idioma inglés, hace que sea menos conocidos los estudios de algoritmos de procesamiento de imágenes médicas. El objetivo general de la presente investigación está centrado en proponer un conjunto de algoritmos para el procesamiento de imágenes con artefacto de endurecimiento de haz en la tomografía computarizada.
MÉTODOS O METODOLOGÍA COMPUTACIONAL
La imagen médica ha revolucionado el diagnóstico de muchas enfermedades. Desde que fue descubierto que los rayos X podían penetrar objetos opacos y proporcionar una imagen de su estructura interna. Desde entonces esta ha sido la herramienta más importante y más ampliamente usada en medicina clínica, tanto como instrumento de diagnóstico como con propósitos terapéuticos.
Una imagen médica, es la representación gráfica de una estructura, región, órgano, o tejido del cuerpo humano que se obtiene a través de procesos físicos y computacionales ordenados para este fin. En términos matemáticos, una imagen médica digital a[m,n] descrita en un espacio discreto de 2D, se puede obtener como resultado de una imagen analógica 𝑎(x, y) en un espacio continuo de 2D a través de un proceso de muestreo, que es referido frecuentemente como digitalización. La imagen continua de 2D 𝑎(x, y) es dividida en N número de filas y M número de columnas. La interacción entre las filas y las columnas se le conoce como píxel (del inglés picture element). El valor asignado a las coordenadas enteras [𝑚, 𝑛] con {m=0, 1,2,…, M-1} y {n=0, 1,2,…, N1} es 𝑎[𝑚, 𝑛] (Peña, y otros, 2016).
Concepto de imágenes tomográficas computarizadas
La modalidad de imagen médica que usa como tipo de energía los rayos X es la radiología, que se divide en las siguientes técnicas de imagen: Radiología convencional, radiología digital, fluoroscopio y TC. Las cuatro técnicas son ionizantes debido a la propia naturaleza de los rayos X, aportan información anatómica o estructural del paciente y la principal fuente de contraste es la densidad del tejido (Claudia, 2012).
La imagen radiológica convencional utiliza los rayos X para irradiar al paciente que son recogidos en una película fotográfica especial, comúnmente denominado placa. Dicha imagen es proyectiva, es decir, representa la suma de todas las estructuras del objeto proyectadas sobre una superficie bidimensional, lo que hace que no sea cuantitativa y dificulta la interpretación por parte del equipo médico (Fuentes, y otros, 2015). Con la aparición de la TC, se elimina el problema de la superposición de tejidos, debido a que con esta técnica se obtienen cortes del paciente (Fig. 1). Según la orientación del plano que corta al paciente se definen los tres tipos de cortes tomográficos: coronal, sagital y axial.

Fig. 1 (Izq.) Esquema de los diferentes planos que forman los llamados cortes tomográficos y (dcha.) ejemplo de imágenes TC de la zona maxilofacial de un paciente: (a) axial, (b) coronal, (c) sagital y (d) reconstrucción tridimensional a partir de numerosos cortes. (Claudia, 2012)
La tomografía, en términos generales, se define como la técnica que permite obtener imágenes de cortes de un objeto sin practicar dicho corte (Cruz, y otros, 2018). La tomografía computarizada es un equipo utilizado para procedimientos diagnósticos con el fin de escanear las diferentes estructuras del cuerpo mediante la combinación de rayos X y tecnología informática (Mayuri, 2018).
La idea central de la tomografía consiste en la reconstrucción de un volumen partiendo de los datos recogidos en las proyecciones (integrales lineales) del mismo. Existen diferentes métodos de reconstrucción que (Peña, y otros, 2016), (Cruz, y otros, 2018) y (Amieiro, 2018) los agruparon en analíticos e iterativos, atendiendo a la base matemática que utilizan a la hora de hacer la inversión (reconstrucción) desde las proyecciones hasta el conjunto de datos original.
Algoritmos de procesamiento de imágenes
El procesamiento digital de imágenes lleva asociada una enorme cantidad de conceptos relacionados con hardware, software y también con desarrollos teóricos. En el momento de desarrollar soluciones que requieran de procesamiento digital de imágenes, es difícil en algunos casos determinar cuáles son las técnicas más adecuadas para el problema en particular, e inclusive a veces se desconocen estas.
El primer paso en el proceso es adquirir la imagen digital. Para ello se necesitan sensores y la capacidad para digitalizar la señal producida por el sensor, en nuestro caso la adquisición es por medio de la TC. Una vez que la imagen digitalizada ha sido obtenida, el siguiente paso consiste en el pre-procesamiento de dicha imagen. El objetivo del pre procesamiento es mejorar la imagen de forma que el objetivo final tenga mayores posibilidades de éxito. El paso siguiente es la segmentación (Peña, y otros, 2016). Definida en sentido amplio, su objetivo es dividir la imagen en las partes que la constituyen o los objetos que la forman.
En último lugar se encuentran el reconocimiento y la interpretación. El reconocimiento es el proceso que asigna una etiqueta a un objeto basada en la información que proporcionan los descriptores (clasificación). La interpretación lleva a asignar significado al conjunto de objetos reconocidos (Figura 2).
Fuente: Elaboración propia.
Una vez que la imagen está digitalizada es posible mejorar la apariencia visual y la calidad de la misma o transformarla de tal forma que facilite su análisis computarizado para una aplicación específica. La calidad de una imagen médica es variable dependiendo de la técnica y máquina de adquisición (Martínez, y otros, 2017). Pueden encontrarse determinados artefactos (característicos de cada tecnología), ruido no homogéneo, iluminación no uniforme, bordes difusos y bajo contraste entre los elementos presentes. Por ello, la extracción de información de la imagen se convierte en una tarea ardua y difícil.
Algoritmos de reconstrucción analíticos
Los algoritmos analíticos tratan de encontrar una expresión analítica que permita hacer la transformada inversa de Radon para pasar del espacio de los datos medidos en el tomógrafo agrupados en proyecciones al espacio de la imagen. Estos algoritmos se basan en el teorema del corte central, que permite relacionar las proyecciones, Pø(t) con la transformada de Fourier de la distribución f(x,y) como se muestra el desarrollo matemático del algoritmo en (García, 2013). El teorema del corte central demostrado en (García , 2013), analiza la transformada de Fourier 2D de la imagen, F(u,v), particularizada en la línea v=0, que resulta coincidir con la transformada de Fourier 1D de la proyección según la trayectoria:
Método directo de Fourier
Según el teorema del corte central, realizando la transformada de Fourier 1D de las proyecciones a diferentes ángulos de un determinado objeto, f(x,y), es posible determinar los valores de la transformada de Fourier 2D del objeto, F(u,v), como explica (Molina, 2012). Si se tomasen infinitas proyecciones, se conocerían todos los puntos de F(u,v) y por tanto, sería posible recuperar perfectamente el objeto f(x,y) utilizando la transformada inversa de Fourier:
Algoritmo de Retroproyección filtrada
La retroproyección filtrada o FBP del inglés Filtered Back Projection es un algoritmo analítico de inversión de la transformada de Radon que hace uso de herramientas matemáticas propias del análisis de Fourier como lo son el teorema de proyecciones y el producto convolución además de una elaborada construcción geométrica que permitirá reconstruir la imagen a partir de un conjunto de rectas (Rodríguez, y otros, 2018).
El algoritmo se compone de tres pasos básicos
Obtención de las proyecciones Pθ(t), a través de las métricas de velocidad, atenuación.
Transformamos las proyecciones (Sθ(ω)=TF{Pθ(t)}) y
Filtramos las proyecciones transformadas (|𝜔|) y retro proyectamos para recuperar f(x,y). Para estimar 𝑓(𝑥,𝑦), este método utiliza el teorema de Fourier (C. Gallardo Llopis, otros 2020)
Definición formal de FBP
El procedimiento clásico de reconstrucción de imagen es la FBP. Este método es rápido y sencillo, pero no utiliza información estadística. Es un buen método para aplicaciones en las que el número de cuentas es alto (como tomografía de rayos X o TC), pero es peor cuando hay un bajo número de cuentas, como en imágenes de medicina nuclear. Los métodos iterativos de reconstrucción de imagen se han propuesto como alternativas a FBP. Estas técnicas tienen un coste computacional más alto que FBP, pero producen imágenes de mejor contraste y relación señal-ruido. Los métodos iterativos eliminan los artefactos de (Espitia, y otros, 2016).
Reconstrucción FDK
FDK es un algoritmo de reconstrucción para tomografía cone beam con trayectoria circular propuesto por Feldkamp, David y Kreis en 1984. Este algoritmo propone una aproximación a 3D de la FBP por lo que también se basa en el teorema del corte central (Molina, 2012).
Para el desarrollo de este algoritmo se estudia el problema como si fuera FBP, introduciendo una tercera coordenada (axial) de forma que se puedan considerar todos los rayos a partir de transformaciones del sistema de coordenadas. Además, para una implementación más eficiente, se suele hacer coincidir el sistema de coordenadas del detector real con el sistema de coordenadas del objeto (detector virtual en la Figura 4).
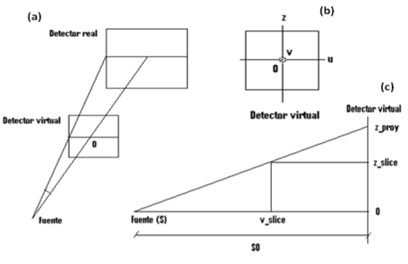
Fig. 3 (a) vista en perspectiva, (b) vista frontal y (c) vista lateral de la geometría cone beam. Para la reconstrucción se harán coincidir el sistema de coordenadas del detector real con el del detector virtual. (Molina, 2012)
En la actualidad aún se utiliza el desarrollo matemático del algoritmo de reconstrucción, que se puede ver en detalle en (Arselan, 2016), en la siguiente fórmula:
Existen muchos algoritmos para el procesamiento entre los que se destacan: el uso de agrupaciones (Menéndez, y otros, 2016), umbralización (López-Portilla, y otros, 2016), (Huérfano, 2015), (Rivero, y otros, 2016), filtro de realce de estructuras esféricas (López-Portilla, y otros, 2016), crecimiento de regiones (Huérfano, 2015), estimación de curvaturas (Damaris, y otros, 2017), aproximaciones geométricas (Rivero, y otros, 2016), histograma (Huérfano, 2015), (López-Portilla, y otros, 2016), (Rivero, y otros, 2016), coincidencia morfológica (Huérfano, 2016) y de los trabajos investigativos que se han dedicado en comparar algoritmos de procesamiento de imágenes tales como: el estudio comparativo realizado por: (Godoy, 2017) con cuatro métodos para la identificación de especies, donde trabaja con los algoritmos de Knn, Decisión Tree y clasificadores Naive Bayes, (Pereira, y otros, 2017) realizó un estudio experimental para comparar el desempeño de Naive Bayes con otros clasificadores bayesianos, donde se destaca el algoritmo Naive Bayes en la clacificación de los pixeles. Los estudios comparativos de (Rivero, y otros, 2016), entre algoritmos de clasificación: “Naive Bayes, Desición Tree and Neural Network” se ve que el algoritmo Naive Bayes fue el mejor con respecto a los demás.
La mayoría de las investigaciones se dedican en la segunda etapa del procesamiento de imágenes donde se seleccionó los más utilizados y que mejores resultados ofrecen como la umbralización, el crecimiento de regiones y para terminar con esta etapa se implementaron cuatro algoritmos detectores de bordes el Canny, Prewitt, Sobel y Roberts. La primera etapa de procesamiento de imagen que se conoce como pre-procesamiento se implementaron los algoritmos de binarización, normalización, en escala de gris, filtro espacial, filtro pasa bajo, filtro mediana y Filtro Butterwort. Estos algoritmos son infalibles en la primera etapa y la última etapa se implementó los algoritmos de extracción de puntos y Transformada de Hough.
RESULTADOS Y DISCUSIÓN
Las imágenes probadas en la herramienta Matlab y para ver el rendimiento de cada algoritmo, son originalmente propiedad del hospital provincial de Ciego de Ávila, un total de 556 imágenes. En este estudio comparativo se analizan el número de aciertos y tiempo de cada algoritmo, obtenidos en cada imagen y se compara los resultados que varían según el algoritmo y la herramienta que se esté usando. La cantidad de aciertos es uno de los factores más importantes que incide en la eficiencia de los algoritmos con lo cual nos permite saber la confianza que proporciona al sistema al procesar imágenes con artefactos de endurecimiento de haz.
Luego de observar los resultados se procede a considerar el algoritmo más adecuado para un exitoso sistema de procesamiento de imagen. Para evaluar el rendimiento de los algoritmos se tuvo en cuenta los siguientes operadores:
Tiempo de Procesamiento: Es el tiempo que requiere el algoritmo para realizar los diferentes procesos.
Aciertos: Se refiere al porcentaje de éxito que tiene el algoritmo que con éxito procesan las imágenes con endurecimiento de haz, si la identifica artefactos y corrige recortada correctamente se considera como éxito, lo contrario se denomina como fracaso. Para llevar un procesamiento de imagen con artefacto de endurecimiento de haz es necesario probar el éxito del algoritmo considerando que el 100% corresponde a las 155 bibliografías consultadas, donde se hizo diversas pruebas y los resultados se obtuvieron aplicando la siguiente fórmula:
Valor medio: se aplicó la fórmula del valor promedio para determinar el valor medio de los resultados encontrados entre las diferentes bibliografías consultadas, aplicando la siguiente fórmula:
A continuación, se muestran las características y los resultados de los algoritmos utilizados en las Figura 4, Figura 5 y Figura 6 y se realiza una valoración sobre los aciertos de cada uno de ellos en el proceso de procesamiento de imágenes en las Tabla 1, Tabla 2 y Tabla 3, para la muestra se utilizó la herramienta de Matlab 2017 Figura 7:
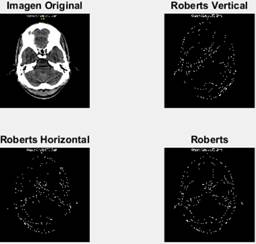
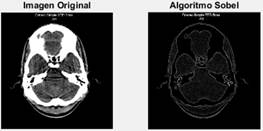
Fig. 4 La imagen original (superior izquierda), detectando bordes verticales (superior derecha), detectando bordes horizontales (inferior izquierda) y bordes totales (inferior derecha).
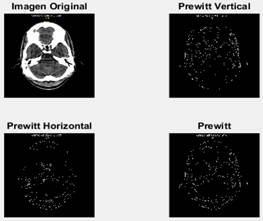
Fig. 5 La imagen original (superior izquierda), detectando bordes verticales (superior derecha), detectando bordes horizontales (inferior izquierda) y bordes totales (inferior derecha).
En el procesamiento de imágenes se trabajó con varios algoritmos comportándose cada uno de ellos de diferentes maneras en correspondencia al tiempo de procesamiento y acierto en el trabajo que se necesitaba como se muestran en las siguientes imágenes A, B C, resaltado que los algoritmos Isodata, y Otsu su diferencia entre el acierto y el tiempo de ejecución son similares véase en la Figura 8, en el procesamiento basado en regiones sucede de igual manera con Cr y DFR.
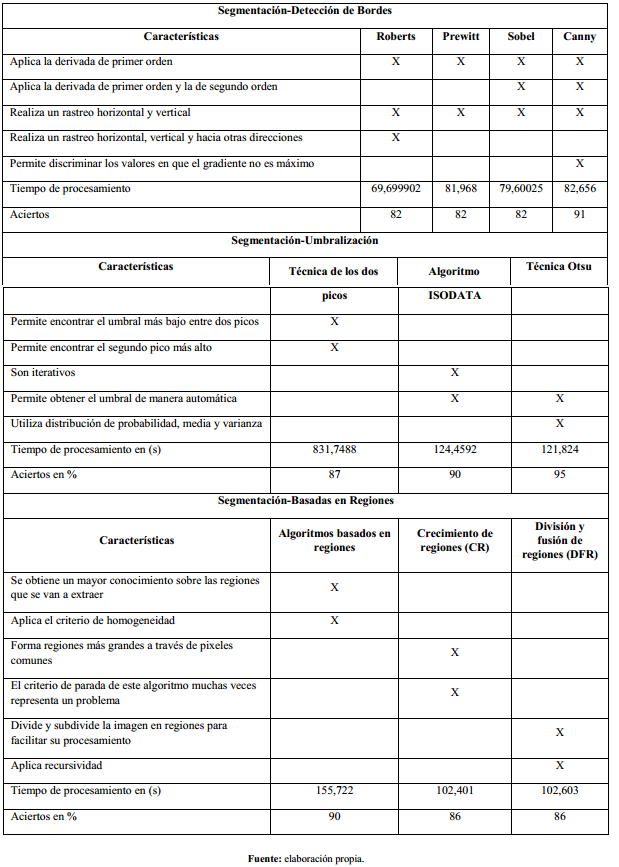
En cuanto en la Tabla 1, la transformada en escala de gris tuvo el mejor tiempo de ejecución de 1,0602s pero un peor acierto de 63%, el procesado del histograma y el filtro de mediana tuvieron el mejor acierto de 91% pero el tiempo de histograma es mejor con 4,7223s con 6,5239s de filtro mediana.
En la tercera etapa del procesamiento están los algoritmos de segmentación localizados en la Tabla 2, donde el detector de bordes Roberts es más rápido con un tiempo de 6,69990s pero peor en el acierto de 82% mientras el detector Canny presenta un tiempo de 82,656s y el acierto 91%, en esta etapa el algoritmo con mejor cierto es Otsu 95% la constancia de los algoritmos basados en umbralización tardan en ejecutar, el Otsu presenta un tiempo de 121, 824s.
En la Tabla 3, el algoritmo Canny es seleccionado para esta etapa de extracción de características, pero con un peor acierto de 89% aunque sea el más rápido con 2,2656s en los algoritmos utilizados para esta etapa está la transformada de Hough con un tiempo de 103,610s y el acierto 91%, el método de puntos de esquina con el tiempo de 102,153s y 90% de acierto.
CONCLUSIONES
Al seleccionar adecuadamente los algoritmos, se puede desarrollar sistema para el tratamiento de imágenes con artefactos de endurecimiento de haz con mayor eficacia, los cuales permitirán mejores diagnósticos y detección temprana de enfermedades.
Para el proceso de reconstrucción de imágenes los métodos iterativos como OSEM, fue el que se destacó más, aunque el costo computacional sea mayor comparado al algoritmo FBP, pero el tiempo de ejecución, su resultado de procesamiento (elimina todos los artefactos, tiene mejor contraste y señal-ruido) es mucho mejor. Así como el procesado de histograma tuvo mejores resultados para el pre-procesamiento, pero con un tiempo de ejecución mayor, el algoritmo Otsu en la segmentación y para extracción de características la transformada de Hough.
Se realizó el estudio de los algoritmos en cada una de las etapas, para seleccionar adecuada de algoritmos de reconstrucción, pre-procesamiento, segmentación y extracción de características en imágenes con endurecimiento de haz.
Como trabajo futuro se propone aplicar los mismos algoritmos existentes para procesar imágenes con otros tipos de artefactos.